人教版七年级数学下册7.2.2用坐标表示平移 课件(共23张PPT)
文档属性
| 名称 | 人教版七年级数学下册7.2.2用坐标表示平移 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
电梯上人的移动
体 验 回 顾
(1)什么叫平移?
在平面内,把一个图形沿某一直线方向移动一定的距离,会得到一个新图形。图形的这种移动叫做平移变换,简称平移。
平移前后形状 ,大小 ,位置 .
不变
不变
改变
(2)平移后得到的新图形与原图形有什么
关系?
体 验 回 顾
-3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(-3,-2)
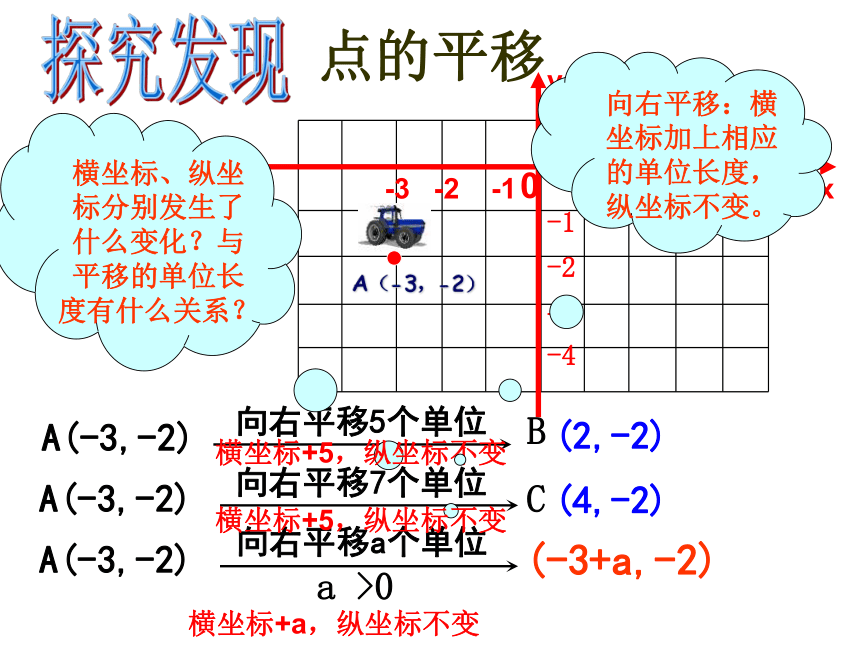
A(-3,-2)
向右平移5个单位
B
(2,-2)
A(-3,-2)
向右平移7个单位
C
(4,-2)
(-3+a,-2)
A(-3,-2)
向右平移a个单位
a >0
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
横坐标+5,纵坐标不变
横坐标+5,纵坐标不变
横坐标+a,纵坐标不变
点的平移
向右平移:横坐标加上相应的单位长度,纵坐标不变。
-4- 3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
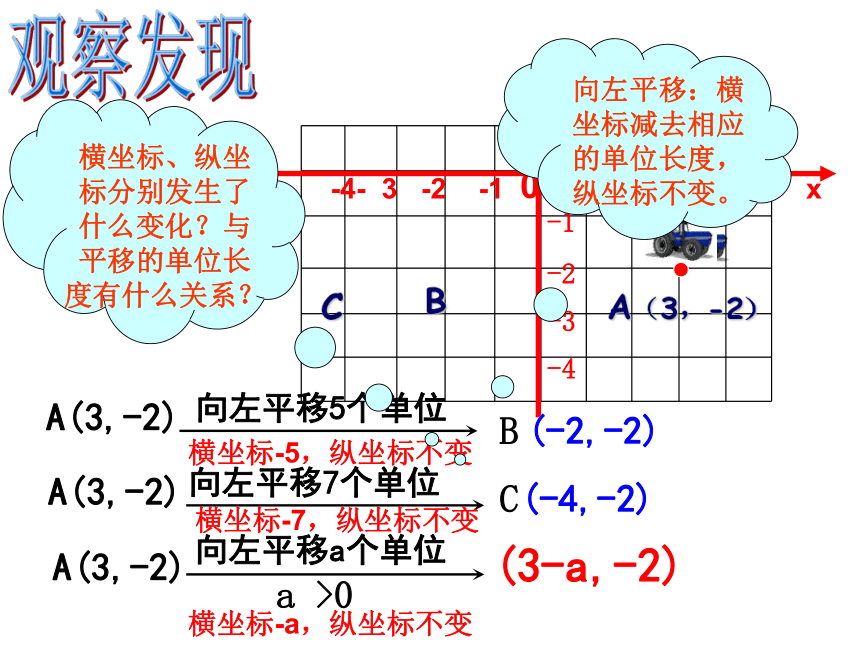
A(3,-2)
A(3,-2)
向左平移5个单位
B
(-2,-2)
B
C
A(3,-2)
向左平移7个单位
C
(-4,-2)
(3-a,-2)
A(3,-2)
向左平移a个单位
a >0
横坐标-5,纵坐标不变
横坐标-7,纵坐标不变
横坐标-a,纵坐标不变
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
向左平移:横坐标减去相应的单位长度,纵坐标不变。
(1)左、右平移:
向右平移a个单位
点(x,y)
向左平移a个单位
点(x,y)
(x+a,y)
(x-a,y)
总结规律1:点的平移与点的坐标变化间的关系
*
1.在平面直角坐标系中,有一点P(-4,2),若将点P:
(1)向左平移2个单位长度,所得点的坐标为__________;
(2)向右平移3个单位长度,所得点的坐标为_____________ ;
(-6,2)
(-1,2)
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
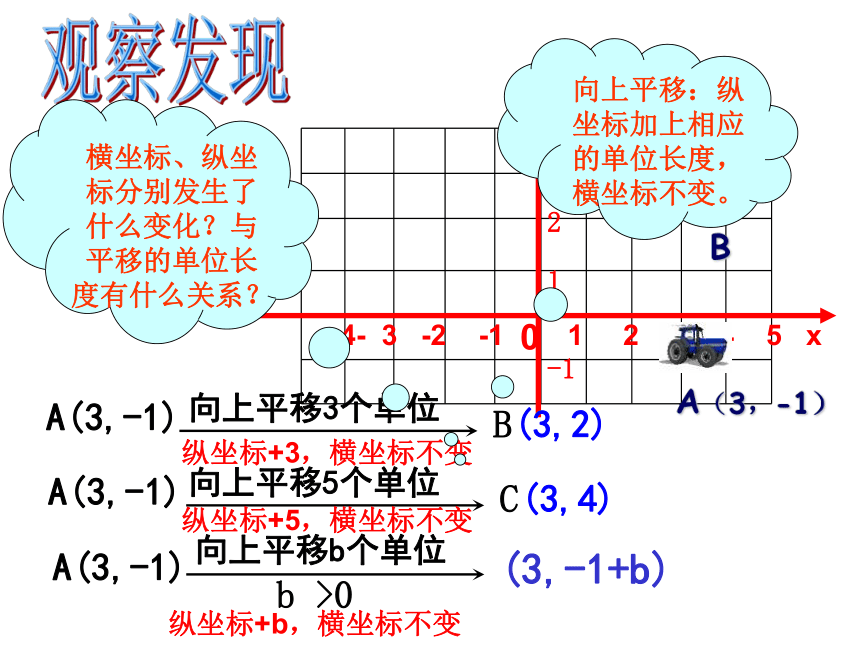
A(3,-1)
A(3,-1)
向上平移3个单位
B
(3,2)
B
C
A(3,-1)
向上平移5个单位
C
(3,4)
(3,-1+b)
A(3,-1)
向上平移b个单位
b >0
纵坐标+5,横坐标不变
纵坐标+3,横坐标不变
纵坐标+b,横坐标不变
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
向上平移:纵坐标加上相应的单位长度,横坐标不变。
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,4)
A(3,4)
向下平移3个单位
B
(3,1)
B
C
A(3,4)
向下平移5个单位
C
(3,-1)
(3,4-b)
A(3,4)
向下平移b个单位
b >0
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
向下平移:纵坐标减去相应的单位长度,横坐标不变。
纵坐标-3,横坐标不变
纵坐标-5,横坐标不变
纵坐标-b,横坐标不变
(2)上、下平移:
向上平移a个单位
点(x,y)
向下平移a个单位
点(x,y)
(x,y+a)
(x,y-a)
总结规律2:点的平移与点的坐标变化间的关系
1.在平面直角坐标系中,有一点P(-4,2),若将点P:
(3)向下平移4个单位长度,所得点的坐标为_____________ ;
(4)向上平移5个单位长度,所得点的坐标为_____________ ;
(-4, -2)
(-4,7)
点(x,y)
左右平移a个单位长度
(x-a,y)
点(x,y)
上下平移b个单位长度
纵变横不变
横变纵不变
左减
(x+a,y)
右加
(x,y+b)
上加
(x,y-b)
下减
*
2、在平面直角坐标系中,有一点P(-4,2),(1)若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_______。
(1,5)
(2)若将P先向上平移3个单位长度,再向右平移5个单位长度,所得坐标为_______。
(1,5)
6
5
4
3 `
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
x
y
①将△ABC三个顶点横坐标减去6,得到A1,B1,C1,连接这3点,得到△A1B1C1; ②将△ABC三个顶点纵坐标减去5,得到A2,B2,C2,连接这3点,得到△A2B2C2.
A (5,4)
C (2,3)
B (3,1)
C1 (-4,3)
A1 (-1,4)
A2 (5,-1)
C2 (2,-2)
B1 (-3,1)
B 2(3,-4)
图形的平移
在此图形平移中对应点的坐标有何关系
在此平移中对应点的坐标有何关系
△A1B1C1可以看作是△ABC向左平移6个单位得到的
△A2B2C2可以看作是△ABC向下平移5个单位得到的。
规律总结:
(1)左、右平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(2)上、下平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(x+a,y)
向右平移a个单位
(x-a,y)
向左平移a个单位
(x,y+b)
(x,y-b)
向上平移b个单位
向下平移b个单位
1.将点A(-3,2)向下平移3个单位,
再向右平移4个单位得点B,则B点坐
标是
2.将点P(0,-2)向左平移2个单位,
再向上平移4个单位得点Q(x,y),则
xy=
(1,-1)
-4
1.把点M(1,2)平移后得到点N(1,-2)
则平移的过程是:
向下平移4个单位
2.把点M(-3,1)平移后得到点N(-1,4)
则平移的过程是:
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
(1)左、右平移:
向右平移a个单位
(a>0)
(2)上、下平移:
原图形上的点(x,y)
向左平移a个单位
(a>0)
原图形上的点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
b>0
原图形上的点(x,y)
向下平移b个单位
b>0
原图形上的点(x,y)
(x,y+b)
(x,y-b)
规律总结:
(1)左、右平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(2)上、下平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(x+a,y)
向右平移a个单位
(x-a,y)
向左平移a个单位
(x,y+b)
(x,y-b)
向上平移b个单位
向下平移b个单位
1、在坐标中描出点A(-2,-3)并进行如下平移:
(1)将点A向右平移5个单位长度得到点B,则 点B点的坐标是 ;
(2)将点A向右平移6个单位长度得到点C,则 点C点的坐标是 ;
(3)将点A向右平移a(a>o)个单位长度得到点D,则 点D点的坐标是 ;
(4)将点A向左平移a(a>o)个单位长度得到点E,则 点E点的坐标是 ;
(3,-3)
(4,-3)
(-2+ a ,-3)
(-2-a ,-3)
2、在坐标中描出点A(-2,-3)并进行如下平移
(1)将点A向上平移5个单位长度得到点B,则 点B点的坐标是 ;
(2)将点A向上平移6个单位长度得到点C,则 点C点的坐标是 ;
(3)将点A向上平移a(a>o)个单位长度得到点D,则 点D点的坐标是 ;
(4)将点A向左下平移a(a>o)个单位长度得到点E ,则 点E点的坐标是 .
(-2,2)
(-2,3)
(-2,-3+ a )
(-2,-3- a )
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗
(2,3)
(4,1)
电梯上人的移动
体 验 回 顾
(1)什么叫平移?
在平面内,把一个图形沿某一直线方向移动一定的距离,会得到一个新图形。图形的这种移动叫做平移变换,简称平移。
平移前后形状 ,大小 ,位置 .
不变
不变
改变
(2)平移后得到的新图形与原图形有什么
关系?
体 验 回 顾
-3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(-3,-2)
A(-3,-2)
向右平移5个单位
B
(2,-2)
A(-3,-2)
向右平移7个单位
C
(4,-2)
(-3+a,-2)
A(-3,-2)
向右平移a个单位
a >0
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
横坐标+5,纵坐标不变
横坐标+5,纵坐标不变
横坐标+a,纵坐标不变
点的平移
向右平移:横坐标加上相应的单位长度,纵坐标不变。
-4- 3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(3,-2)
A(3,-2)
向左平移5个单位
B
(-2,-2)
B
C
A(3,-2)
向左平移7个单位
C
(-4,-2)
(3-a,-2)
A(3,-2)
向左平移a个单位
a >0
横坐标-5,纵坐标不变
横坐标-7,纵坐标不变
横坐标-a,纵坐标不变
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
向左平移:横坐标减去相应的单位长度,纵坐标不变。
(1)左、右平移:
向右平移a个单位
点(x,y)
向左平移a个单位
点(x,y)
(x+a,y)
(x-a,y)
总结规律1:点的平移与点的坐标变化间的关系
*
1.在平面直角坐标系中,有一点P(-4,2),若将点P:
(1)向左平移2个单位长度,所得点的坐标为__________;
(2)向右平移3个单位长度,所得点的坐标为_____________ ;
(-6,2)
(-1,2)
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,-1)
A(3,-1)
向上平移3个单位
B
(3,2)
B
C
A(3,-1)
向上平移5个单位
C
(3,4)
(3,-1+b)
A(3,-1)
向上平移b个单位
b >0
纵坐标+5,横坐标不变
纵坐标+3,横坐标不变
纵坐标+b,横坐标不变
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
向上平移:纵坐标加上相应的单位长度,横坐标不变。
-4- 3 -2 -1 1 2 3 4 5 x
y
0
4
2
1
3
-1
A(3,4)
A(3,4)
向下平移3个单位
B
(3,1)
B
C
A(3,4)
向下平移5个单位
C
(3,-1)
(3,4-b)
A(3,4)
向下平移b个单位
b >0
横坐标、纵坐标分别发生了什么变化?与平移的单位长度有什么关系?
向下平移:纵坐标减去相应的单位长度,横坐标不变。
纵坐标-3,横坐标不变
纵坐标-5,横坐标不变
纵坐标-b,横坐标不变
(2)上、下平移:
向上平移a个单位
点(x,y)
向下平移a个单位
点(x,y)
(x,y+a)
(x,y-a)
总结规律2:点的平移与点的坐标变化间的关系
1.在平面直角坐标系中,有一点P(-4,2),若将点P:
(3)向下平移4个单位长度,所得点的坐标为_____________ ;
(4)向上平移5个单位长度,所得点的坐标为_____________ ;
(-4, -2)
(-4,7)
点(x,y)
左右平移a个单位长度
(x-a,y)
点(x,y)
上下平移b个单位长度
纵变横不变
横变纵不变
左减
(x+a,y)
右加
(x,y+b)
上加
(x,y-b)
下减
*
2、在平面直角坐标系中,有一点P(-4,2),(1)若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_______。
(1,5)
(2)若将P先向上平移3个单位长度,再向右平移5个单位长度,所得坐标为_______。
(1,5)
6
5
4
3 `
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
-4
-5
x
y
①将△ABC三个顶点横坐标减去6,得到A1,B1,C1,连接这3点,得到△A1B1C1; ②将△ABC三个顶点纵坐标减去5,得到A2,B2,C2,连接这3点,得到△A2B2C2.
A (5,4)
C (2,3)
B (3,1)
C1 (-4,3)
A1 (-1,4)
A2 (5,-1)
C2 (2,-2)
B1 (-3,1)
B 2(3,-4)
图形的平移
在此图形平移中对应点的坐标有何关系
在此平移中对应点的坐标有何关系
△A1B1C1可以看作是△ABC向左平移6个单位得到的
△A2B2C2可以看作是△ABC向下平移5个单位得到的。
规律总结:
(1)左、右平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(2)上、下平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(x+a,y)
向右平移a个单位
(x-a,y)
向左平移a个单位
(x,y+b)
(x,y-b)
向上平移b个单位
向下平移b个单位
1.将点A(-3,2)向下平移3个单位,
再向右平移4个单位得点B,则B点坐
标是
2.将点P(0,-2)向左平移2个单位,
再向上平移4个单位得点Q(x,y),则
xy=
(1,-1)
-4
1.把点M(1,2)平移后得到点N(1,-2)
则平移的过程是:
向下平移4个单位
2.把点M(-3,1)平移后得到点N(-1,4)
则平移的过程是:
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
(1)左、右平移:
向右平移a个单位
(a>0)
(2)上、下平移:
原图形上的点(x,y)
向左平移a个单位
(a>0)
原图形上的点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
b>0
原图形上的点(x,y)
向下平移b个单位
b>0
原图形上的点(x,y)
(x,y+b)
(x,y-b)
规律总结:
(1)左、右平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(2)上、下平移:
原图形上的点(x,y) ,
原图形上的点(x,y) ,
(x+a,y)
向右平移a个单位
(x-a,y)
向左平移a个单位
(x,y+b)
(x,y-b)
向上平移b个单位
向下平移b个单位
1、在坐标中描出点A(-2,-3)并进行如下平移:
(1)将点A向右平移5个单位长度得到点B,则 点B点的坐标是 ;
(2)将点A向右平移6个单位长度得到点C,则 点C点的坐标是 ;
(3)将点A向右平移a(a>o)个单位长度得到点D,则 点D点的坐标是 ;
(4)将点A向左平移a(a>o)个单位长度得到点E,则 点E点的坐标是 ;
(3,-3)
(4,-3)
(-2+ a ,-3)
(-2-a ,-3)
2、在坐标中描出点A(-2,-3)并进行如下平移
(1)将点A向上平移5个单位长度得到点B,则 点B点的坐标是 ;
(2)将点A向上平移6个单位长度得到点C,则 点C点的坐标是 ;
(3)将点A向上平移a(a>o)个单位长度得到点D,则 点D点的坐标是 ;
(4)将点A向左下平移a(a>o)个单位长度得到点E ,则 点E点的坐标是 .
(-2,2)
(-2,3)
(-2,-3+ a )
(-2,-3- a )
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗
(2,3)
(4,1)
