人教版七年级数学下册6.3 实数 课件(共23张PPT)
文档属性
| 名称 | 人教版七年级数学下册6.3 实数 课件(共23张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 997.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:43:51 | ||
图片预览






文档简介
(共23张PPT)
6.3 实 数
有理数
整数
分数
无限不循环小数
有理数
正有理数
0
负有理数
正整数
正分数
负整数
负分数
课前复习:
正整数
0
负整数
1.有理数有哪些分类?
正分数
负分数
(1)
(2)
课前复习:
2.有理数与数轴上的点有什么关系?
任何有理数都可以用数轴上的一个点来表示;
但数轴上的点不一定都表示有理数。
请将下列分数写成小数的形式,你有什么发现?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
探索新知
你认为小数除了上述类型外,还会有什么类型的小数?
无限不循环的小数
探索新知
请两组同学按号互问互答,判断它们是有理数还是无理数?
无限不循环的小数 -- 叫做无理数.
举出一些无理数的例子 如:
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕
无理数的概念:无限不循环小数叫无理数.
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
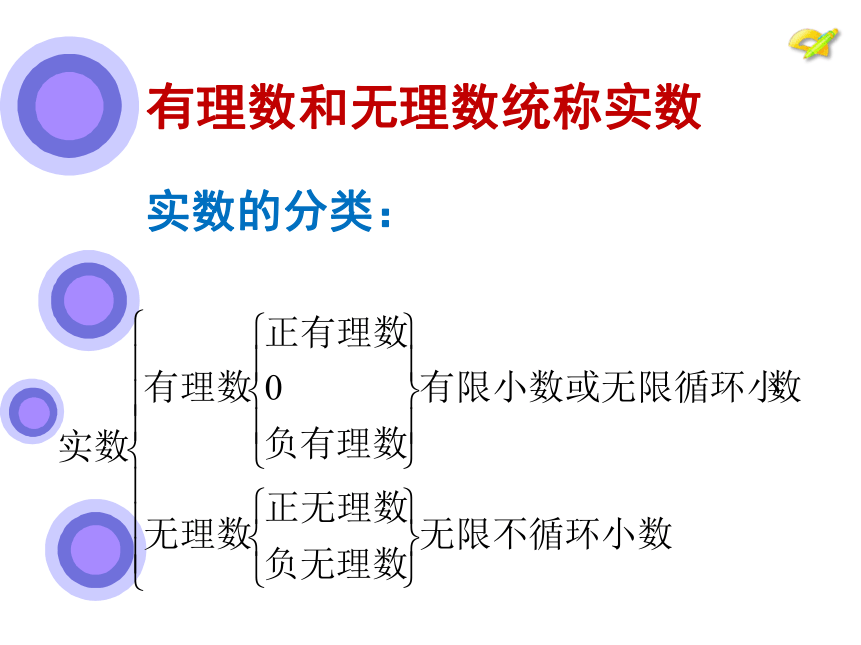
实数的分类:
有理数和无理数统称实数
因为非0有理数和无理数都有正负之分,那么你能类比有理数的分类方法,按大小关系对实数分类吗?
正有理数
正无理数
负有理数
负无理数
实数
有理数
无理数
无限不循环小数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
归纳实数的分类:
正有理数
正无理数
0
有限小数或无限循环小数
你能在数轴上找到表示π的点吗
0
1
2
4
3
-1
-2
π
如图,直径为1个单位长度的圆从原点沿数轴向右
滚动一周,圆上的一点由原点到达点 ,点 对应
的数是多少?
周长
无理数能否可以用数轴上的点表示出来?
可以看出 的长是这个圆的—— ,所以 点对应的数是 .
回忆一下拼成的面积为 2 的大正方形的边长应该是多少呢?
有多大呢?
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
事实上:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
试一试
你能把 在数轴上表示出来吗?请与同桌一起试一试。
结论:每一个有理数和无理数都可以用______上
的一个点表示出来.实数与数轴上的点就是
的,即每一个实数都可以用______上的点来表示;
反过来,数轴上的每一个点都是表示一个 .
实数与数轴上的点
数轴
一一对应
数轴
实数
5,3.14,0, , , , ,- π,
0.1010010001……(相邻两个1之间0的个数逐次加1).
练习1.下列实数中,哪些是有理数?哪些是无理数?
运用新知
练习2.判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
练习3.把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
运用新知
练习4、有下列说法:
①有理数和数轴上的点一一对应;
②不带根号的数一定是有理数;
③负数没有立方根;
④
是17的平方根。其中正确的有( ) (A)0个 (B)1个
(C)2个 (D)3个
运用新知
归纳小结
(1)实数
___________
_______________________________________
1、有理数和无理数统称为
2、实数的分类
(2)实数
_____实数
_____
_____实数
无理数
正有理数
负有理数
有限小数或无限循环小数
___________________________________________
正无理数
负无理数
无限不循环小数
正
0
负
实数
3、实数与数轴上的点是 ___ 的.
4、学习反思:________________________
_____________________________________.
一一对应
0
有理数
课后作业
1、若无理数a满足:1<a<4,请写出两个你熟
悉的无理数:_____,______.
必做题:
课后作业
6.3 实 数
有理数
整数
分数
无限不循环小数
有理数
正有理数
0
负有理数
正整数
正分数
负整数
负分数
课前复习:
正整数
0
负整数
1.有理数有哪些分类?
正分数
负分数
(1)
(2)
课前复习:
2.有理数与数轴上的点有什么关系?
任何有理数都可以用数轴上的一个点来表示;
但数轴上的点不一定都表示有理数。
请将下列分数写成小数的形式,你有什么发现?
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
探索新知
你认为小数除了上述类型外,还会有什么类型的小数?
无限不循环的小数
探索新知
请两组同学按号互问互答,判断它们是有理数还是无理数?
无限不循环的小数 -- 叫做无理数.
举出一些无理数的例子 如:
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕
无理数的概念:无限不循环小数叫无理数.
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
实数的分类:
有理数和无理数统称实数
因为非0有理数和无理数都有正负之分,那么你能类比有理数的分类方法,按大小关系对实数分类吗?
正有理数
正无理数
负有理数
负无理数
实数
有理数
无理数
无限不循环小数
实数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
归纳实数的分类:
正有理数
正无理数
0
有限小数或无限循环小数
你能在数轴上找到表示π的点吗
0
1
2
4
3
-1
-2
π
如图,直径为1个单位长度的圆从原点沿数轴向右
滚动一周,圆上的一点由原点到达点 ,点 对应
的数是多少?
周长
无理数能否可以用数轴上的点表示出来?
可以看出 的长是这个圆的—— ,所以 点对应的数是 .
回忆一下拼成的面积为 2 的大正方形的边长应该是多少呢?
有多大呢?
0
1
2
4
3
-1
-2
问题:边长为1的正方形,对角线长为多少
事实上:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
试一试
你能把 在数轴上表示出来吗?请与同桌一起试一试。
结论:每一个有理数和无理数都可以用______上
的一个点表示出来.实数与数轴上的点就是
的,即每一个实数都可以用______上的点来表示;
反过来,数轴上的每一个点都是表示一个 .
实数与数轴上的点
数轴
一一对应
数轴
实数
5,3.14,0, , , , ,- π,
0.1010010001……(相邻两个1之间0的个数逐次加1).
练习1.下列实数中,哪些是有理数?哪些是无理数?
运用新知
练习2.判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
练习3.把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.
运用新知
练习4、有下列说法:
①有理数和数轴上的点一一对应;
②不带根号的数一定是有理数;
③负数没有立方根;
④
是17的平方根。其中正确的有( ) (A)0个 (B)1个
(C)2个 (D)3个
运用新知
归纳小结
(1)实数
___________
_______________________________________
1、有理数和无理数统称为
2、实数的分类
(2)实数
_____实数
_____
_____实数
无理数
正有理数
负有理数
有限小数或无限循环小数
___________________________________________
正无理数
负无理数
无限不循环小数
正
0
负
实数
3、实数与数轴上的点是 ___ 的.
4、学习反思:________________________
_____________________________________.
一一对应
0
有理数
课后作业
1、若无理数a满足:1<a<4,请写出两个你熟
悉的无理数:_____,______.
必做题:
课后作业
