10.4中心对称同步练习2021—2022学年华东师大版数学七年级下册
文档属性
| 名称 | 10.4中心对称同步练习2021—2022学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 15:09:09 | ||
图片预览



文档简介
10.4中心对称
★在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
★中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.
★把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
★在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称。
★判断一个图形是不是中心对称图形,关键是找到对称中心,可以把图倒过来看(相当于旋转180°),如果看到的图形与原来的图形完全相同,就是中心对称图形,否则就不是。判断一个图形是不是轴对称图形,就是看是否存在一条直线(对称轴),使得这个图形沿这条直线对折后两边能否重合
★(1)画一个点关于某点(对称中心)的对称点的画法是先连结这个点与对称中心并延长一倍即可.
(2)画一个图形关于某点的对称图形的画法是先画出图形中的几个特殊点(如多边形的顶点、线段的端点、圆的圆心等)关于某点的对称点,然后再顺次连结有关对称点即可。
一.选择题(共11小题)
1.下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
A. B.
C. D.
2.下列四个图形中,既是轴对称图形又是中心对称图形的有( )个
A.0 B.1 C.2 D.3
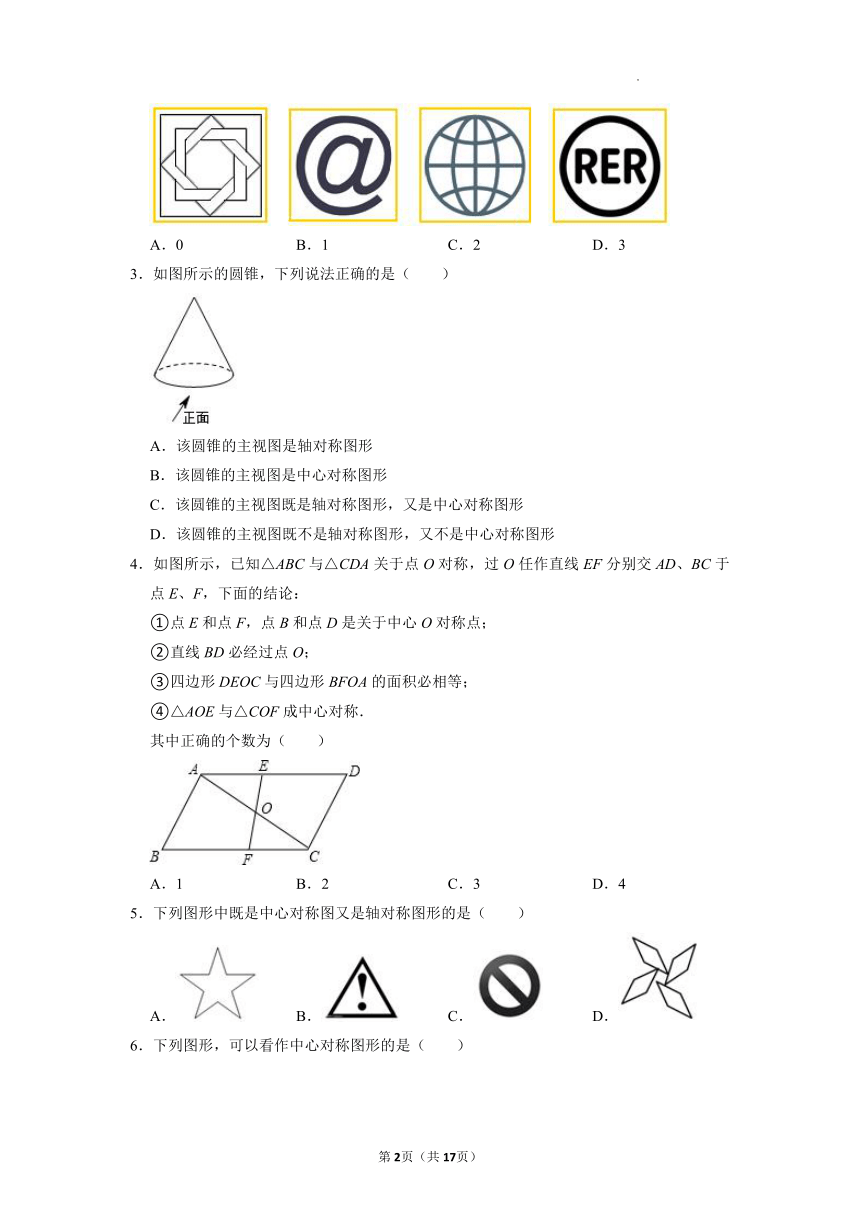
3.如图所示的圆锥,下列说法正确的是( )
A.该圆锥的主视图是轴对称图形
B.该圆锥的主视图是中心对称图形
C.该圆锥的主视图既是轴对称图形,又是中心对称图形
D.该圆锥的主视图既不是轴对称图形,又不是中心对称图形
4.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1 B.2 C.3 D.4
5.下列图形中既是中心对称图又是轴对称图形的是( )
A. B. C. D.
6.下列图形,可以看作中心对称图形的是( )
A. B.
C. D.
7.以下是我国部分博物馆标志的图案,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
8.四组图形中成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
9.下列说法中,正确的是( )
A.在成中心对称的图形中,连接对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连接对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点.那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
10.顺次连接正六边形的三个不相邻的顶点.得到如图所示的图形,该图形( )
A.既是轴对称图形也是中心对称图形
B.是轴对称图形但并不是中心对称图形
C.是中心对称图形但并不是轴对称图形
D.既不是轴对称图形也不是中心对称图形
11.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D都是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共3小题)
12.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE=OD,下列说法中:
①这两个“心”形关于点O成中心对称;
②点C,E是以点O为对称中心的一对对称点;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.
正确的有 .(只填你认为正确的说法的序号)
13.如图,△ABC与△DEF关于O点成中心对称.则AB DE,BC∥ ,AC= .
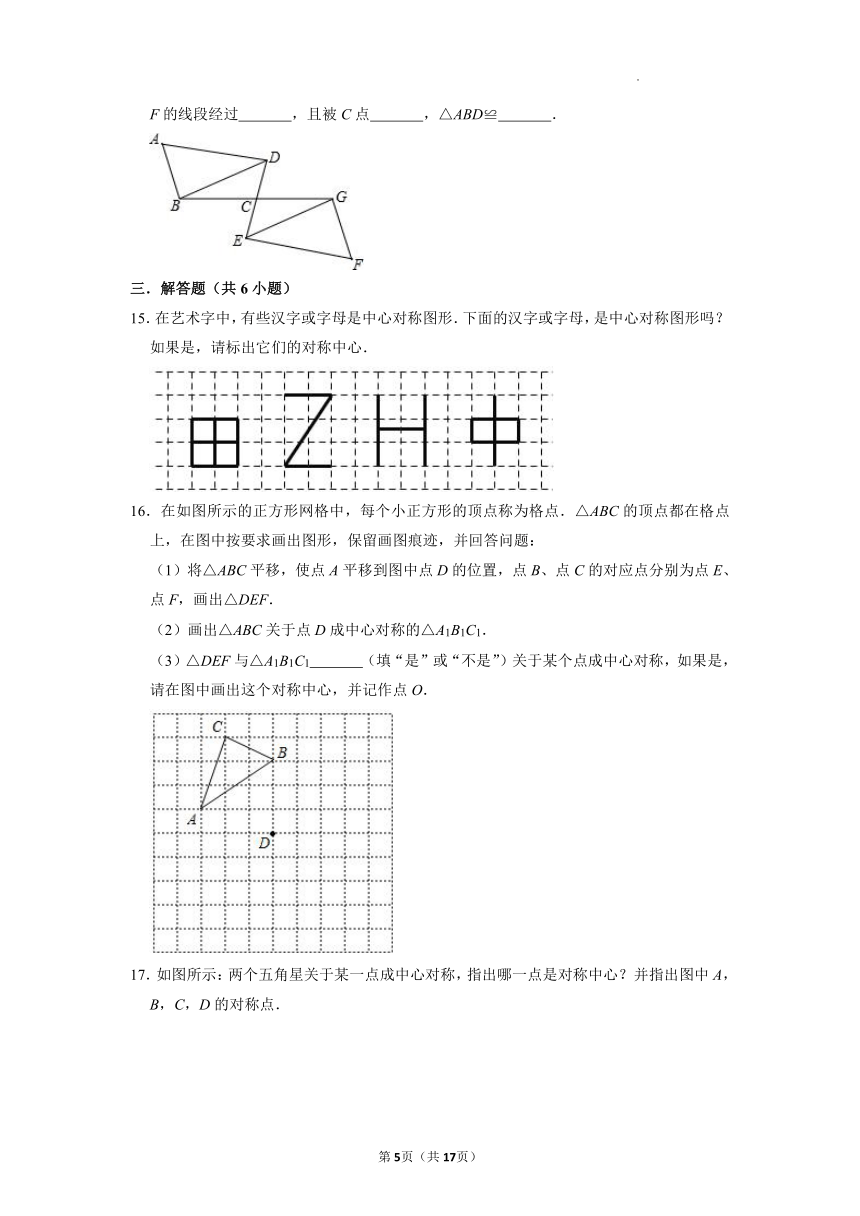
14.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是 ,点A的对称点是 ,E的对称点是 .BD∥ 且BD= .连接A,F的线段经过 ,且被C点 ,△ABD≌ .
三.解答题(共6小题)
15.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
16.在如图所示的正方形网格中,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,在图中按要求画出图形,保留画图痕迹,并回答问题:
(1)将△ABC平移,使点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1 (填“是”或“不是”)关于某个点成中心对称,如果是,请在图中画出这个对称中心,并记作点O.
17.如图所示:两个五角星关于某一点成中心对称,指出哪一点是对称中心?并指出图中A,B,C,D的对称点.
18.在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.
(1)画出此中心对称图形的对称中心O;
(2)画出将△A1B1C1沿直线DE方向向上平移5格得到的△A2B2C2;
(3)求出△CC1C2的面积.
19.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个面积相等的格点正方形,并涂上阴影,使这两个格点正方形无重叠(可以有一个点或一条边重合),且与原正方形组成的图形是轴对称图形,请问这个格点正方形的作法共有几种?并在下面两图中分别画出一种.
20.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 .
10.4中心对称
参考答案与试题解析
一.选择题(共11小题)
1.下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意;
D.不是中心对称图形,故本选项不合题意.
故选:C.
2.下列四个图形中,既是轴对称图形又是中心对称图形的有( )个
A.0 B.1 C.2 D.3
【解答】解:第1个图形,不是轴对称图形,是中心对称图形,故此选项不合题意;
第2个图形,既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
第3个图形,既是轴对称图形,又是中心对称图形,故此选项符合题意;
第4个图形,既不是轴对称图形,也不是中心对称图形,故此选项不合题意.
故选:B.
3.如图所示的圆锥,下列说法正确的是( )
A.该圆锥的主视图是轴对称图形
B.该圆锥的主视图是中心对称图形
C.该圆锥的主视图既是轴对称图形,又是中心对称图形
D.该圆锥的主视图既不是轴对称图形,又不是中心对称图形
【解答】解:圆锥的主视图是等腰三角形,是轴对称图形,但不是中心对称图形,
故选:A.
4.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1 B.2 C.3 D.4
【解答】解:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,
所以四边形ABCD是平行四边形,即点O就是 ABCD的对称中心,则有:
(1)点E和点F,B和D是关于中心O的对称点,正确;
(2)直线BD必经过点O,正确;
(3)四边形DEOC与四边形BFOA的面积必相等,正确;
(5)△AOE与△COF成中心对称,正确;
其中正确的个数为4个,
故选:D.
5.下列图形中既是中心对称图又是轴对称图形的是( )
A. B. C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.是轴对称图形,是中心对称图形,故本选项符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不合题意.
故选:C.
6.下列图形,可以看作中心对称图形的是( )
A. B.
C. D.
【解答】解:A、不是中心对称图形,故本选项不符合题意;
B、是中心对称图形,故本选项符合题意;
C、不是中心对称图形,故本选项不符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:B.
7.以下是我国部分博物馆标志的图案,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,又是中心对称图形,符合题意;
B.是轴对称图形,不是中心对称图形,不符合题意;
C.不是轴对称图形,是中心对称图形,不符合题意;
D.不是轴对称图形,又不是中心对称图形,不符合题意.
故选:A.
8.四组图形中成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
【解答】解:根据中心对称的定义,知(1)、(2)、(3)都成中心对称;(4)显然不是成中心对称.
故选:C.
9.下列说法中,正确的是( )
A.在成中心对称的图形中,连接对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连接对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点.那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
【解答】解:A、一定经过对称中心,错误;
B、正确;
C、必须被该点平分,才能够成中心对称,错误;
D、错误.
故选:B.
10.顺次连接正六边形的三个不相邻的顶点.得到如图所示的图形,该图形( )
A.既是轴对称图形也是中心对称图形
B.是轴对称图形但并不是中心对称图形
C.是中心对称图形但并不是轴对称图形
D.既不是轴对称图形也不是中心对称图形
【解答】解:此图形是等边三角形,等边三角形是轴对称图形但并不是中心对称图形,
故选:B.
11.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D都是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
【解答】解:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,
所以四边形ABCD是平行四边形,即点O就是 ABCD的对称中心,则有:
①点E和点F,B和D是关于中心O的对称点,正确;
②直线BD必经过点O,正确;
③四边形ABCD是中心对称图形,正确;
④∵四边形ABCD是平行四边形,
∴四边形DEOC与四边形BFOA成中心对称,
∴四边形DEOC与四边形BFOA的面积必相等,正确;
⑤△AOE与△COF成中心对称,正确;
其中正确的个数为5个,
故选:D.
二.填空题(共3小题)
12.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE=OD,下列说法中:
①这两个“心”形关于点O成中心对称;
②点C,E是以点O为对称中心的一对对称点;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.
正确的有 ② .(只填你认为正确的说法的序号)
【解答】解:①这两个“心”形关于点O成中心对称,该结论不一定成立;
②∵点C,O,E在同一条直线上,OC=OE,
∴点C,E是以点O为对称中心的一对对称点;说法正确;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB,该结论不一定成立;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形,该结论不一定成立.
所以正确的有②.
故答案为:②.
13.如图,△ABC与△DEF关于O点成中心对称.则AB = DE,BC∥ EF ,AC= DF .
【解答】解:∵△ABC与△DEF关于O点成中心对称
∴△ABC≌△DEF
AB=DE,AC=DF
又∵BO=OE,CO=OF,∠BOC=∠FOE
∴△BOC≌△EOF
∴∠BCO=∠OFE
BC∥EF
故填:=,EF,DF
14.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是 C ,点A的对称点是 F ,E的对称点是 D .BD∥ EG 且BD= EG .连接A,F的线段经过 C ,且被C点 平分 ,△ABD≌ △FGE .
【解答】解:四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是C,点A的对称点是F,E的对称点是D.
BD∥EG且BD=EG.
连接A,F的线段经过C,且被C点平分,△ABD≌△FGE.
故答案为:C、F、D、EG、EG、C、平分、△FGE.
三.解答题(共6小题)
15.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
【解答】解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.
16.在如图所示的正方形网格中,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,在图中按要求画出图形,保留画图痕迹,并回答问题:
(1)将△ABC平移,使点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1 是 (填“是”或“不是”)关于某个点成中心对称,如果是,请在图中画出这个对称中心,并记作点O.
【解答】解:(1)如图所示,△DEF即为所求.
(2)如图所示,△A1B1C1即为所求.
(3)如图所示,△DEF与△A1B1C1是关于点O成中心对称.
故答案为:是.
17.如图所示:两个五角星关于某一点成中心对称,指出哪一点是对称中心?并指出图中A,B,C,D的对称点.
【解答】解:点A是对称中心.
图中A,B,C,D的对称点分别是A、G、H、E.
18.在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.
(1)画出此中心对称图形的对称中心O;
(2)画出将△A1B1C1沿直线DE方向向上平移5格得到的△A2B2C2;
(3)求出△CC1C2的面积.
【解答】解:(1)连接CC1,BB1,交于点O,点O为所求的点;
(2)如图所示,△A2B2C2为所求的三角形;
(3)连接CC2,C1C2,如图所示,
则△CC1C2的面积S=×5×4=10.
19.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个面积相等的格点正方形,并涂上阴影,使这两个格点正方形无重叠(可以有一个点或一条边重合),且与原正方形组成的图形是轴对称图形,请问这个格点正方形的作法共有几种?并在下面两图中分别画出一种.
【解答】解:如图,由图易知这个格点正方形的作法共有4 种.
20.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 关于直线CO成轴对称 .
【解答】解:(1)如图,A1B1C1D1即为所求;
(2)如图,A2B2C2D2即为所求;
(3)关于直线CO成轴对称.
故答案为:关于直线CO成轴对称.
第1页(共1页)
★在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
★中心对称图形都是旋转对称图形,但旋转对称图形不一定是中心对称图形.
★把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
★在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分。
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称。
★判断一个图形是不是中心对称图形,关键是找到对称中心,可以把图倒过来看(相当于旋转180°),如果看到的图形与原来的图形完全相同,就是中心对称图形,否则就不是。判断一个图形是不是轴对称图形,就是看是否存在一条直线(对称轴),使得这个图形沿这条直线对折后两边能否重合
★(1)画一个点关于某点(对称中心)的对称点的画法是先连结这个点与对称中心并延长一倍即可.
(2)画一个图形关于某点的对称图形的画法是先画出图形中的几个特殊点(如多边形的顶点、线段的端点、圆的圆心等)关于某点的对称点,然后再顺次连结有关对称点即可。
一.选择题(共11小题)
1.下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
A. B.
C. D.
2.下列四个图形中,既是轴对称图形又是中心对称图形的有( )个
A.0 B.1 C.2 D.3
3.如图所示的圆锥,下列说法正确的是( )
A.该圆锥的主视图是轴对称图形
B.该圆锥的主视图是中心对称图形
C.该圆锥的主视图既是轴对称图形,又是中心对称图形
D.该圆锥的主视图既不是轴对称图形,又不是中心对称图形
4.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1 B.2 C.3 D.4
5.下列图形中既是中心对称图又是轴对称图形的是( )
A. B. C. D.
6.下列图形,可以看作中心对称图形的是( )
A. B.
C. D.
7.以下是我国部分博物馆标志的图案,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
8.四组图形中成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
9.下列说法中,正确的是( )
A.在成中心对称的图形中,连接对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连接对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点.那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
10.顺次连接正六边形的三个不相邻的顶点.得到如图所示的图形,该图形( )
A.既是轴对称图形也是中心对称图形
B.是轴对称图形但并不是中心对称图形
C.是中心对称图形但并不是轴对称图形
D.既不是轴对称图形也不是中心对称图形
11.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D都是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共3小题)
12.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE=OD,下列说法中:
①这两个“心”形关于点O成中心对称;
②点C,E是以点O为对称中心的一对对称点;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.
正确的有 .(只填你认为正确的说法的序号)
13.如图,△ABC与△DEF关于O点成中心对称.则AB DE,BC∥ ,AC= .
14.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是 ,点A的对称点是 ,E的对称点是 .BD∥ 且BD= .连接A,F的线段经过 ,且被C点 ,△ABD≌ .
三.解答题(共6小题)
15.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
16.在如图所示的正方形网格中,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,在图中按要求画出图形,保留画图痕迹,并回答问题:
(1)将△ABC平移,使点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1 (填“是”或“不是”)关于某个点成中心对称,如果是,请在图中画出这个对称中心,并记作点O.
17.如图所示:两个五角星关于某一点成中心对称,指出哪一点是对称中心?并指出图中A,B,C,D的对称点.
18.在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.
(1)画出此中心对称图形的对称中心O;
(2)画出将△A1B1C1沿直线DE方向向上平移5格得到的△A2B2C2;
(3)求出△CC1C2的面积.
19.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个面积相等的格点正方形,并涂上阴影,使这两个格点正方形无重叠(可以有一个点或一条边重合),且与原正方形组成的图形是轴对称图形,请问这个格点正方形的作法共有几种?并在下面两图中分别画出一种.
20.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 .
10.4中心对称
参考答案与试题解析
一.选择题(共11小题)
1.下列四幅图案是四所大学校徽的主体标识,其中是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意;
D.不是中心对称图形,故本选项不合题意.
故选:C.
2.下列四个图形中,既是轴对称图形又是中心对称图形的有( )个
A.0 B.1 C.2 D.3
【解答】解:第1个图形,不是轴对称图形,是中心对称图形,故此选项不合题意;
第2个图形,既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
第3个图形,既是轴对称图形,又是中心对称图形,故此选项符合题意;
第4个图形,既不是轴对称图形,也不是中心对称图形,故此选项不合题意.
故选:B.
3.如图所示的圆锥,下列说法正确的是( )
A.该圆锥的主视图是轴对称图形
B.该圆锥的主视图是中心对称图形
C.该圆锥的主视图既是轴对称图形,又是中心对称图形
D.该圆锥的主视图既不是轴对称图形,又不是中心对称图形
【解答】解:圆锥的主视图是等腰三角形,是轴对称图形,但不是中心对称图形,
故选:A.
4.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )
A.1 B.2 C.3 D.4
【解答】解:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,
所以四边形ABCD是平行四边形,即点O就是 ABCD的对称中心,则有:
(1)点E和点F,B和D是关于中心O的对称点,正确;
(2)直线BD必经过点O,正确;
(3)四边形DEOC与四边形BFOA的面积必相等,正确;
(5)△AOE与△COF成中心对称,正确;
其中正确的个数为4个,
故选:D.
5.下列图形中既是中心对称图又是轴对称图形的是( )
A. B. C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.是轴对称图形,是中心对称图形,故本选项符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不合题意.
故选:C.
6.下列图形,可以看作中心对称图形的是( )
A. B.
C. D.
【解答】解:A、不是中心对称图形,故本选项不符合题意;
B、是中心对称图形,故本选项符合题意;
C、不是中心对称图形,故本选项不符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:B.
7.以下是我国部分博物馆标志的图案,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,又是中心对称图形,符合题意;
B.是轴对称图形,不是中心对称图形,不符合题意;
C.不是轴对称图形,是中心对称图形,不符合题意;
D.不是轴对称图形,又不是中心对称图形,不符合题意.
故选:A.
8.四组图形中成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
【解答】解:根据中心对称的定义,知(1)、(2)、(3)都成中心对称;(4)显然不是成中心对称.
故选:C.
9.下列说法中,正确的是( )
A.在成中心对称的图形中,连接对称点的线段不一定都经过对称中心
B.在成中心对称的图形中,连接对称点的线段都被对称中心平分
C.若两个图形的对应点连成的线段都经过某一点.那么这两个图形一定关于这一点成中心对称
D.以上说法都正确
【解答】解:A、一定经过对称中心,错误;
B、正确;
C、必须被该点平分,才能够成中心对称,错误;
D、错误.
故选:B.
10.顺次连接正六边形的三个不相邻的顶点.得到如图所示的图形,该图形( )
A.既是轴对称图形也是中心对称图形
B.是轴对称图形但并不是中心对称图形
C.是中心对称图形但并不是轴对称图形
D.既不是轴对称图形也不是中心对称图形
【解答】解:此图形是等边三角形,等边三角形是轴对称图形但并不是中心对称图形,
故选:B.
11.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D都是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
【解答】解:△ABC与△CDA关于点O对称,则AB=CD、AD=BC,
所以四边形ABCD是平行四边形,即点O就是 ABCD的对称中心,则有:
①点E和点F,B和D是关于中心O的对称点,正确;
②直线BD必经过点O,正确;
③四边形ABCD是中心对称图形,正确;
④∵四边形ABCD是平行四边形,
∴四边形DEOC与四边形BFOA成中心对称,
∴四边形DEOC与四边形BFOA的面积必相等,正确;
⑤△AOE与△COF成中心对称,正确;
其中正确的个数为5个,
故选:D.
二.填空题(共3小题)
12.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE=OD,下列说法中:
①这两个“心”形关于点O成中心对称;
②点C,E是以点O为对称中心的一对对称点;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.
正确的有 ② .(只填你认为正确的说法的序号)
【解答】解:①这两个“心”形关于点O成中心对称,该结论不一定成立;
②∵点C,O,E在同一条直线上,OC=OE,
∴点C,E是以点O为对称中心的一对对称点;说法正确;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB,该结论不一定成立;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形,该结论不一定成立.
所以正确的有②.
故答案为:②.
13.如图,△ABC与△DEF关于O点成中心对称.则AB = DE,BC∥ EF ,AC= DF .
【解答】解:∵△ABC与△DEF关于O点成中心对称
∴△ABC≌△DEF
AB=DE,AC=DF
又∵BO=OE,CO=OF,∠BOC=∠FOE
∴△BOC≌△EOF
∴∠BCO=∠OFE
BC∥EF
故填:=,EF,DF
14.如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是 C ,点A的对称点是 F ,E的对称点是 D .BD∥ EG 且BD= EG .连接A,F的线段经过 C ,且被C点 平分 ,△ABD≌ △FGE .
【解答】解:四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是C,点A的对称点是F,E的对称点是D.
BD∥EG且BD=EG.
连接A,F的线段经过C,且被C点平分,△ABD≌△FGE.
故答案为:C、F、D、EG、EG、C、平分、△FGE.
三.解答题(共6小题)
15.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
【解答】解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.
16.在如图所示的正方形网格中,每个小正方形的顶点称为格点.△ABC的顶点都在格点上,在图中按要求画出图形,保留画图痕迹,并回答问题:
(1)将△ABC平移,使点A平移到图中点D的位置,点B、点C的对应点分别为点E、点F,画出△DEF.
(2)画出△ABC关于点D成中心对称的△A1B1C1.
(3)△DEF与△A1B1C1 是 (填“是”或“不是”)关于某个点成中心对称,如果是,请在图中画出这个对称中心,并记作点O.
【解答】解:(1)如图所示,△DEF即为所求.
(2)如图所示,△A1B1C1即为所求.
(3)如图所示,△DEF与△A1B1C1是关于点O成中心对称.
故答案为:是.
17.如图所示:两个五角星关于某一点成中心对称,指出哪一点是对称中心?并指出图中A,B,C,D的对称点.
【解答】解:点A是对称中心.
图中A,B,C,D的对称点分别是A、G、H、E.
18.在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心对称图形.
(1)画出此中心对称图形的对称中心O;
(2)画出将△A1B1C1沿直线DE方向向上平移5格得到的△A2B2C2;
(3)求出△CC1C2的面积.
【解答】解:(1)连接CC1,BB1,交于点O,点O为所求的点;
(2)如图所示,△A2B2C2为所求的三角形;
(3)连接CC2,C1C2,如图所示,
则△CC1C2的面积S=×5×4=10.
19.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个面积相等的格点正方形,并涂上阴影,使这两个格点正方形无重叠(可以有一个点或一条边重合),且与原正方形组成的图形是轴对称图形,请问这个格点正方形的作法共有几种?并在下面两图中分别画出一种.
【解答】解:如图,由图易知这个格点正方形的作法共有4 种.
20.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 关于直线CO成轴对称 .
【解答】解:(1)如图,A1B1C1D1即为所求;
(2)如图,A2B2C2D2即为所求;
(3)关于直线CO成轴对称.
故答案为:关于直线CO成轴对称.
第1页(共1页)
