10.3.1图形的旋转+同步练习++2021—2022学年华东师大版数学七年级下册
文档属性
| 名称 | 10.3.1图形的旋转+同步练习++2021—2022学年华东师大版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 15:33:20 | ||
图片预览



文档简介
10.3.1图形的旋转
★图形的旋转在平面内,将一个图形绕一个定点沿某个方向转动一个角度的图形变换叫做旋转,定点o叫做旋转中心,转动的角度叫做旋转角.如果图形上的点 P 经过旋转变为点 P ’,那么这两个点叫做这个旋转的对应点.
注:旋转中心、旋转方向 旋转角是确定旋转的关键,图形在旋转的过程中,只改变图形的位置而不改变其形状和大小.
★线段旋转90°后与原来的线段互相垂直.
★旋转变换中的“三点注意”:
在旋转的过程中,图形中位置不发生变化的点为旋转中心;
在旋转的过程中,有多个角都可以表示旋转角;
(3)旋转的范围是在平面内旋转,否则有可能旋转为立体图形、
一.选择题(共9小题)
1.将图绕中心按顺时针方向旋转60°后可得到的图形是( )
A. B.
C. D.
2.在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( )
A.顺时针旋转90°,向下平移
B.逆时针旋转90°,向下平移
C.顺时针旋转90°,向右平移
D.逆时针旋转90°,向右平移
3.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则其旋转中心一定是( )
A.点E B.点F C.点G D.点H
4.如图,四边形AOBC绕点O顺时针方向旋转得到四边形DOEF,下列说法正确的是( )
A.旋转角是∠BOD
B.AO=EO
C.若连接CO,FO,则CO=FO
D.四边形AOBC和四边形DOEF可能不全等
5.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转45° D.逆时针旋转45°
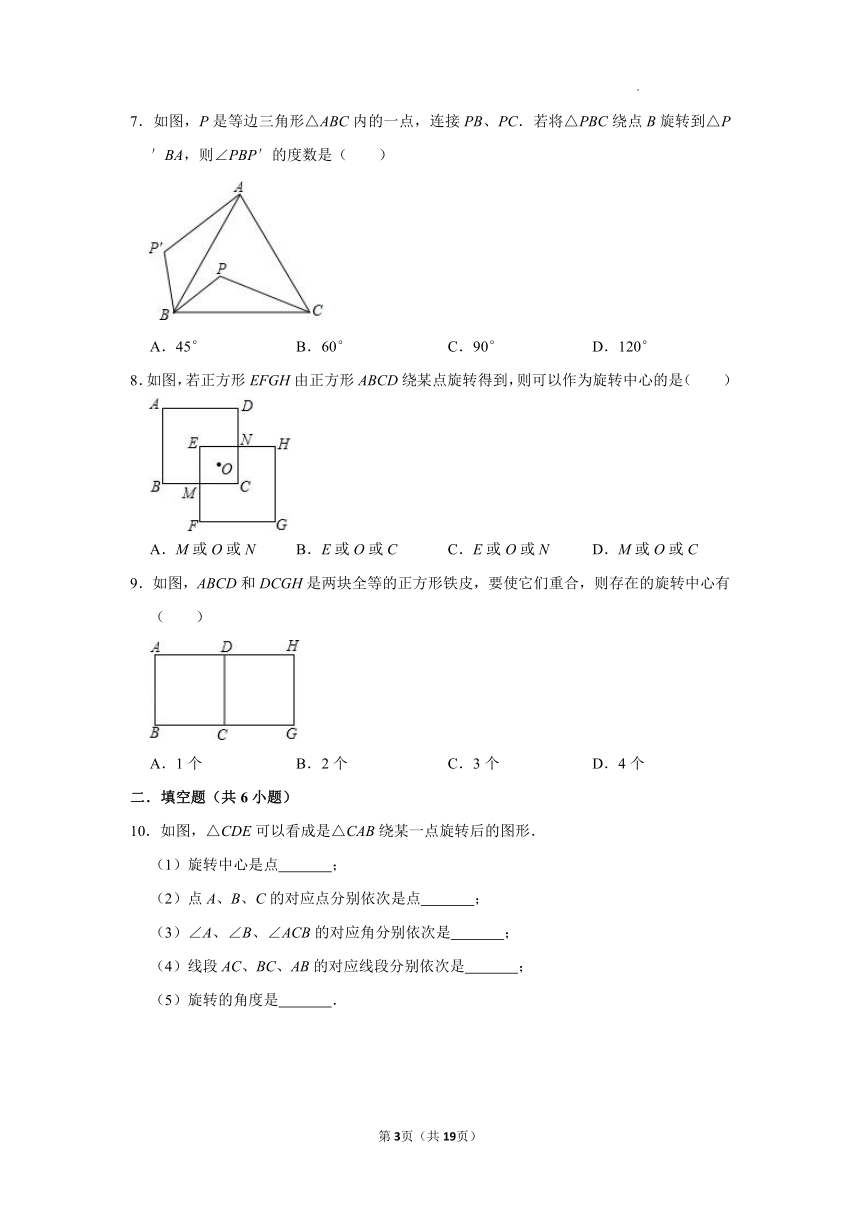
7.如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
A.45° B.60° C.90° D.120°
8.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.M或O或N B.E或O或C C.E或O或N D.M或O或C
9.如图,ABCD和DCGH是两块全等的正方形铁皮,要使它们重合,则存在的旋转中心有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题)
10.如图,△CDE可以看成是△CAB绕某一点旋转后的图形.
(1)旋转中心是点 ;
(2)点A、B、C的对应点分别依次是点 ;
(3)∠A、∠B、∠ACB的对应角分别依次是 ;
(4)线段AC、BC、AB的对应线段分别依次是 ;
(5)旋转的角度是 .
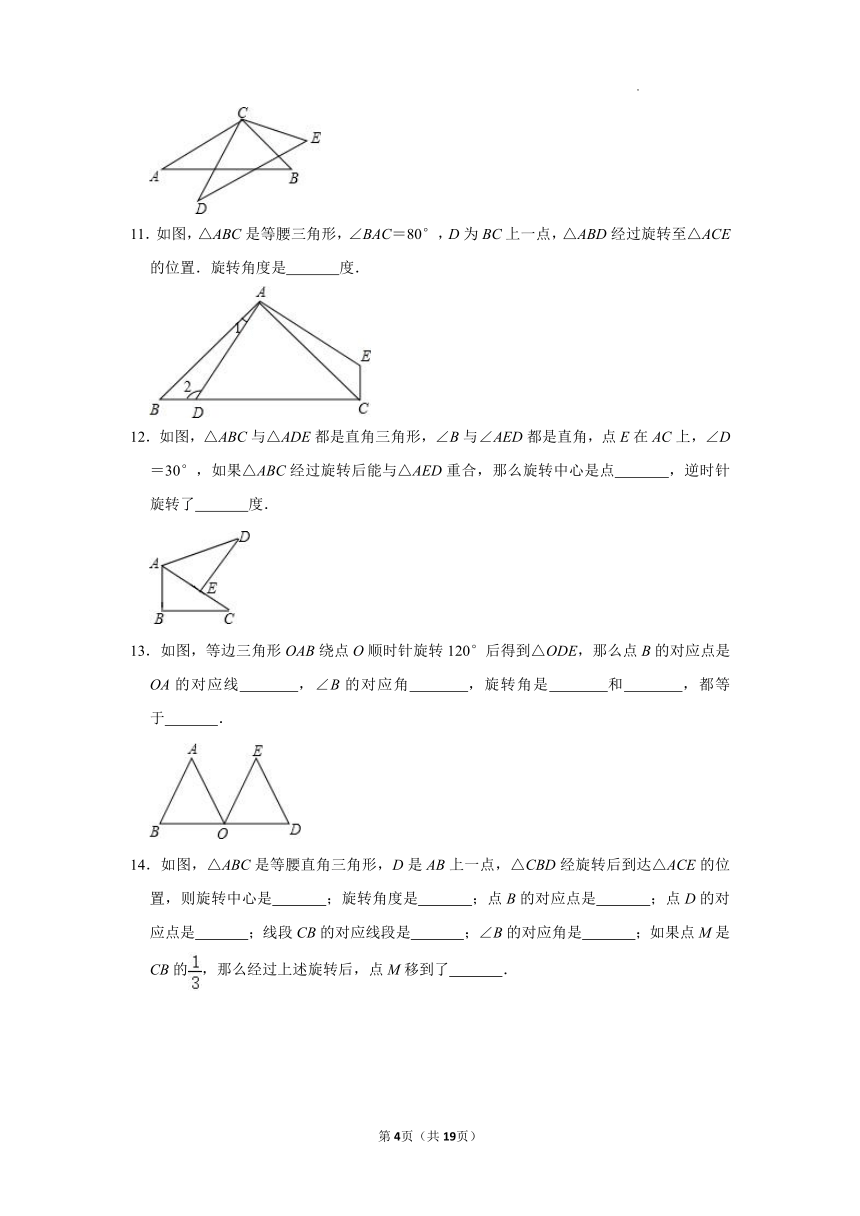
11.如图,△ABC是等腰三角形,∠BAC=80°,D为BC上一点,△ABD经过旋转至△ACE的位置.旋转角度是 度.
12.如图,△ABC与△ADE都是直角三角形,∠B与∠AED都是直角,点E在AC上,∠D=30°,如果△ABC经过旋转后能与△AED重合,那么旋转中心是点 ,逆时针旋转了 度.
13.如图,等边三角形OAB绕点O顺时针旋转120°后得到△ODE,那么点B的对应点是 OA的对应线 ,∠B的对应角 ,旋转角是 和 ,都等于 .
14.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△ACE的位置,则旋转中心是 ;旋转角度是 ;点B的对应点是 ;点D的对应点是 ;线段CB的对应线段是 ;∠B的对应角是 ;如果点M是CB的,那么经过上述旋转后,点M移到了 .
15.如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是 (在下列各图中选填正确图形的序号即可)
三.解答题(共6小题)
16.钟表的时针匀速旋转一周需要12小时,如图:
(1)指出它的旋转中心;
(2)经过5小时整,时针旋转了多少度?
17.如图,△ABC是等腰三角形,∠BAC=40°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M在AB上,且AM=BM,那么经过上述旋转后,点M转到了什么位置?
18.如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达△ACE的位置,那么:
(1)旋转中心是点 ;
(2)点B、D的对应点分别是点 ;
(3)线段AB、BD、DA的对应线段分别是 ;
(4)∠B的对应角是 ;
(5)旋转角度为 ;
(6)△ACE的形状为 .
19.如图所示,△ACD和△BCE都是等边三角形,△DCB经过旋转后得到△ACE.
(1)指出旋转中心是哪一点?
(2)旋转了多少度?
(3)图中还存在是旋转关系的三角形吗?
20.如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
(1)点A的对应点是点 ,线段AB的对应线段是 ,∠D的对应角是 ;
(2)旋转中心是 ,∠BCB'的大小是 ,四边形A′B′CD′的形状是 ;
(3)在四边形A′B′CD′中与线段AD相等的线段有 .
21.如图,△ABE为等腰三角形,经旋转后得到△FDG,其中四边形ABCD为正方形,
试问:
(1)旋转中心为哪个点?
(2)旋转角为多少度?
(3)指出∠E的对应角及BE的对应边.
10.3.1图形的旋转
参考答案与试题解析
一.选择题(共9小题)
1.将图绕中心按顺时针方向旋转60°后可得到的图形是( )
A. B.
C. D.
【解答】解:将图绕中心按顺时针方向旋转60°后得到的图形是.
故选:A.
2.在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( )
A.顺时针旋转90°,向下平移
B.逆时针旋转90°,向下平移
C.顺时针旋转90°,向右平移
D.逆时针旋转90°,向右平移
【解答】解:观察图形可知,出现的小方格需顺时针旋转90°,向右平移至边界.
故选:C.
3.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则其旋转中心一定是( )
A.点E B.点F C.点G D.点H
【解答】解:根据旋转的性质,知:旋转中心,一定在对应点所连线段的垂直平分线上.
则其旋转中心是NN1和PP1的垂直平分线的交点,即点G.
故选:C.
4.如图,四边形AOBC绕点O顺时针方向旋转得到四边形DOEF,下列说法正确的是( )
A.旋转角是∠BOD
B.AO=EO
C.若连接CO,FO,则CO=FO
D.四边形AOBC和四边形DOEF可能不全等
【解答】解:∵四边形AOBC绕点O顺时针方向旋转得到四边形DOEF,
∴旋转角是∠AOD,OA=OD,四边形AOBC和四边形DOEF全等,故A、B、D选项错误;
若连接CO,FO,则CO=FO,故C选项正确,
故选:C.
5.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
【解答】解:现将数字“69”旋转180°,得到的数字是:69.
故选:B.
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转45° D.逆时针旋转45°
【解答】解:根据图形可知:将△ABC绕点A逆时针旋转90°可得到△ADE.
故选:B.
7.如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
A.45° B.60° C.90° D.120°
【解答】解:∵将△PBC绕点B旋转到△P′BA,
∴∠ABP′=∠CBP,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABP′+∠ABP=60°,
∴∠PBP′=60°,
故选:B.
8.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.M或O或N B.E或O或C C.E或O或N D.M或O或C
【解答】解:若以M为旋转中心,把正方形ABCD顺时针旋转90°,A点对应点为H,B点对应点为E,C点对应点为F,D点对应点为G,则可得到正方形EFGH;
若以O为旋转中心,把正方形ABCD旋转180°,A点对应点为G,B点对应点为H,C点对应点为E,D点对应点为F,则可得到正方形EFGH;
若以N为旋转中心,把正方形ABCD逆时针旋转90°,A点对应点为F,B点对应点为G,C点对应点为H,D点对应点为E,则可得到正方形EFGH.
故选:A.
9.如图,ABCD和DCGH是两块全等的正方形铁皮,要使它们重合,则存在的旋转中心有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:根据旋转的性质,可得要使正方形ABCD和DCGH重合,有3种方法,可以分别绕D、C或CD的中点旋转,
即旋转中心有3个.故选C.
二.填空题(共6小题)
10.如图,△CDE可以看成是△CAB绕某一点旋转后的图形.
(1)旋转中心是点 C ;
(2)点A、B、C的对应点分别依次是点 D、E、C ;
(3)∠A、∠B、∠ACB的对应角分别依次是 ∠D、∠E、∠DCE ;
(4)线段AC、BC、AB的对应线段分别依次是 DC、EC、DE ;
(5)旋转的角度是 ∠ACD的度数(或∠BCE的度数) .
【解答】解:(1)旋转中心是点C;
(2)点A、B、C的对应点分别依次是点D、E、C;
(3)∠A、∠B、∠ACB的对应角分别依次是∠D、∠E、∠DCE;
(4)线段AC、BC、AB的对应线段分别依次是DC、EC、DE;
(5)旋转的角度是∠ACD的度数(或∠BCE的度数).
故答案为:(1)C;(2)D、E、C;(3)∠D、∠E、∠DCE;(4)DC、EC、DE;(5)∠ACD的度数(或∠BCE的度数).
11.如图,△ABC是等腰三角形,∠BAC=80°,D为BC上一点,△ABD经过旋转至△ACE的位置.旋转角度是 80 度.
【解答】解:∵△ABD经过旋转至△ACE的位置,
∴旋转后AB对应AC,则旋转角等于∠BAC;
∵∠BAC=80°,
∴旋转角度是80°.
故答案为80.
12.如图,△ABC与△ADE都是直角三角形,∠B与∠AED都是直角,点E在AC上,∠D=30°,如果△ABC经过旋转后能与△AED重合,那么旋转中心是点 A ,逆时针旋转了 60 度.
【解答】解:根据题意,得
AC的对应边是AD,因此旋转的中心是点A,
旋转的度数是∠EAD的度数,即∠EAD的度数=90°﹣30°=60°.
故答案为A,60;
13.如图,等边三角形OAB绕点O顺时针旋转120°后得到△ODE,那么点B的对应点是 点E OA的对应线 OD ,∠B的对应角 ∠E ,旋转角是 ∠BOE 和 ∠AOD ,都等于 120° .
【解答】解:如图,∵等边三角形OAB绕点O顺时针旋转120°后得到△ODE,
∴△OAB≌△ODE,∠AOD=∠BOE=120°,
∴OB=OE,OA=OD,∠B=∠E,
∴点B的对应点是点E,OA的对应线OD,∠B的对应角∠E,旋转角是∠BOE和∠AOD,都等于120°.
故答案是:点E,OD,∠E,∠BOE和∠AOD,120°.
14.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△ACE的位置,则旋转中心是 点C ;旋转角度是 90° ;点B的对应点是 点A ;点D的对应点是 点E ;线段CB的对应线段是 CA ;∠B的对应角是 ∠EAC ;如果点M是CB的,那么经过上述旋转后,点M移到了 点N处 .
【解答】解:根据图形分析可知,△CBD绕点C顺时针旋转90度后到达△ACE的位置,
故旋转中心是点C;
旋转角度是∠BCA=90°;
点B的对应点是点A;
点D的对应点是点E;
线段CB的对应点是CA;
∠B的对应角是∠EAC;
如果点M是CB的,那么经过上述旋转后,点M移到了点N处.
15.如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是 (4) (在下列各图中选填正确图形的序号即可)
【解答】解:观察图形,将图形(1)以点O为旋转中心,每次顺时针旋转90°,得到下一个图形,每旋转四次回到原来的位置,
而2015=503×4+3,
所以第2015次旋转后的图形与(4)一样.
故答案为(4).
三.解答题(共6小题)
16.钟表的时针匀速旋转一周需要12小时,如图:
(1)指出它的旋转中心;
(2)经过5小时整,时针旋转了多少度?
【解答】解:(1)钟表圆盘的中心位置;
(2)∵钟表上的刻度把圆周12等分.
∴每一等分所对的圆心角是360°÷12=30°.
时针经过5小时整,需要旋转5格,即旋转角为30°×5=150°.
17.如图,△ABC是等腰三角形,∠BAC=40°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M在AB上,且AM=BM,那么经过上述旋转后,点M转到了什么位置?
【解答】解:(1)因为△ABD经旋转后到达△ACE,它们的公共顶点为A,所以旋转中心是点A;
(2)线段AB旋转后,对应边是AC,∠BAC就是旋转角,因为∠BAC=40°,所以旋转了40°;
(3)因为旋转前后AB,AC是对应边,故AB的中点M,旋转后就是AC的中点了,所以点M转到了AC的中点.
18.如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达△ACE的位置,那么:
(1)旋转中心是点 A ;
(2)点B、D的对应点分别是点 C、E ;
(3)线段AB、BD、DA的对应线段分别是 线段AC、CE、EA ;
(4)∠B的对应角是 ∠ACE ;
(5)旋转角度为 60° ;
(6)△ACE的形状为 直角三角形 .
【解答】解:∵△ABD经过旋转后到达△ACE的位置,
∴(1)旋转中心是点A;
故答案为:A;
(2)点B、D的对应点分别是点C、E;
故答案为:点C、E;
(3)线段AB、BD、DA的对应线段分别是线段AC、CE、EA;
故答案为:线段AC、CE、EA;
(4)∠B的对应角是∠ACE;
故答案为:∠ACE;
(5)旋转角度为∠BAC=60°;
故答案为:60°;
(6)∵△ABC是等边三角形,D是BC边上的中点,
∴∠ADB=90°,
∴∠AEC=90°,
∴△ACE的形状为直角三角形.
故答案为:直角三角形.
19.如图所示,△ACD和△BCE都是等边三角形,△DCB经过旋转后得到△ACE.
(1)指出旋转中心是哪一点?
(2)旋转了多少度?
(3)图中还存在是旋转关系的三角形吗?
【解答】解:(1)∵△ACD和△BCE都是等边三角形,
∴CD=CA,CE=CB,∠ACD=∠BCE=60°,
∴△DCB绕点C逆时针旋转60°得到△ACE;
∴旋转中心为点C;
(2)旋转角为60°;
(3)△PCE绕点C顺时针旋转60°得到△QCB;△DCQ绕点C逆时针旋转60°得到△ACP.
20.如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
(1)点A的对应点是点 A′ ,线段AB的对应线段是 A′B′ ,∠D的对应角是 ∠D′ ;
(2)旋转中心是 点C ,∠BCB'的大小是 45° ,四边形A′B′CD′的形状是 长方形 ;
(3)在四边形A′B′CD′中与线段AD相等的线段有 A′D′、B′C .
【解答】解:(1)点A的对应点是点A',线段AB的对应线段是A'B',∠D的对应角是∠D';
(2)旋转中心是点C,∠BCB'的大小是45°,四边形A'B'CD'的形状是长方形;
(3)在四边形A'B'CD'中与线段AD相等的线段有A'D'、B'C.
21.如图,△ABE为等腰三角形,经旋转后得到△FDG,其中四边形ABCD为正方形,
试问:
(1)旋转中心为哪个点?
(2)旋转角为多少度?
(3)指出∠E的对应角及BE的对应边.
【解答】解:(1)如图所示:△ABE绕C点顺时针旋转90度,可得到△FDG,
即旋转中心为C点;
(2)△ABE绕C点顺时针旋转90度,可得到△FDG,
旋转角为90度;
(3)由(1)得:∠E的对应角为∠G,BE的对应边为DG.
第1页(共1页)
★图形的旋转在平面内,将一个图形绕一个定点沿某个方向转动一个角度的图形变换叫做旋转,定点o叫做旋转中心,转动的角度叫做旋转角.如果图形上的点 P 经过旋转变为点 P ’,那么这两个点叫做这个旋转的对应点.
注:旋转中心、旋转方向 旋转角是确定旋转的关键,图形在旋转的过程中,只改变图形的位置而不改变其形状和大小.
★线段旋转90°后与原来的线段互相垂直.
★旋转变换中的“三点注意”:
在旋转的过程中,图形中位置不发生变化的点为旋转中心;
在旋转的过程中,有多个角都可以表示旋转角;
(3)旋转的范围是在平面内旋转,否则有可能旋转为立体图形、
一.选择题(共9小题)
1.将图绕中心按顺时针方向旋转60°后可得到的图形是( )
A. B.
C. D.
2.在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( )
A.顺时针旋转90°,向下平移
B.逆时针旋转90°,向下平移
C.顺时针旋转90°,向右平移
D.逆时针旋转90°,向右平移
3.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则其旋转中心一定是( )
A.点E B.点F C.点G D.点H
4.如图,四边形AOBC绕点O顺时针方向旋转得到四边形DOEF,下列说法正确的是( )
A.旋转角是∠BOD
B.AO=EO
C.若连接CO,FO,则CO=FO
D.四边形AOBC和四边形DOEF可能不全等
5.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转45° D.逆时针旋转45°
7.如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
A.45° B.60° C.90° D.120°
8.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.M或O或N B.E或O或C C.E或O或N D.M或O或C
9.如图,ABCD和DCGH是两块全等的正方形铁皮,要使它们重合,则存在的旋转中心有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题)
10.如图,△CDE可以看成是△CAB绕某一点旋转后的图形.
(1)旋转中心是点 ;
(2)点A、B、C的对应点分别依次是点 ;
(3)∠A、∠B、∠ACB的对应角分别依次是 ;
(4)线段AC、BC、AB的对应线段分别依次是 ;
(5)旋转的角度是 .
11.如图,△ABC是等腰三角形,∠BAC=80°,D为BC上一点,△ABD经过旋转至△ACE的位置.旋转角度是 度.
12.如图,△ABC与△ADE都是直角三角形,∠B与∠AED都是直角,点E在AC上,∠D=30°,如果△ABC经过旋转后能与△AED重合,那么旋转中心是点 ,逆时针旋转了 度.
13.如图,等边三角形OAB绕点O顺时针旋转120°后得到△ODE,那么点B的对应点是 OA的对应线 ,∠B的对应角 ,旋转角是 和 ,都等于 .
14.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△ACE的位置,则旋转中心是 ;旋转角度是 ;点B的对应点是 ;点D的对应点是 ;线段CB的对应线段是 ;∠B的对应角是 ;如果点M是CB的,那么经过上述旋转后,点M移到了 .
15.如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是 (在下列各图中选填正确图形的序号即可)
三.解答题(共6小题)
16.钟表的时针匀速旋转一周需要12小时,如图:
(1)指出它的旋转中心;
(2)经过5小时整,时针旋转了多少度?
17.如图,△ABC是等腰三角形,∠BAC=40°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M在AB上,且AM=BM,那么经过上述旋转后,点M转到了什么位置?
18.如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达△ACE的位置,那么:
(1)旋转中心是点 ;
(2)点B、D的对应点分别是点 ;
(3)线段AB、BD、DA的对应线段分别是 ;
(4)∠B的对应角是 ;
(5)旋转角度为 ;
(6)△ACE的形状为 .
19.如图所示,△ACD和△BCE都是等边三角形,△DCB经过旋转后得到△ACE.
(1)指出旋转中心是哪一点?
(2)旋转了多少度?
(3)图中还存在是旋转关系的三角形吗?
20.如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
(1)点A的对应点是点 ,线段AB的对应线段是 ,∠D的对应角是 ;
(2)旋转中心是 ,∠BCB'的大小是 ,四边形A′B′CD′的形状是 ;
(3)在四边形A′B′CD′中与线段AD相等的线段有 .
21.如图,△ABE为等腰三角形,经旋转后得到△FDG,其中四边形ABCD为正方形,
试问:
(1)旋转中心为哪个点?
(2)旋转角为多少度?
(3)指出∠E的对应角及BE的对应边.
10.3.1图形的旋转
参考答案与试题解析
一.选择题(共9小题)
1.将图绕中心按顺时针方向旋转60°后可得到的图形是( )
A. B.
C. D.
【解答】解:将图绕中心按顺时针方向旋转60°后得到的图形是.
故选:A.
2.在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( )
A.顺时针旋转90°,向下平移
B.逆时针旋转90°,向下平移
C.顺时针旋转90°,向右平移
D.逆时针旋转90°,向右平移
【解答】解:观察图形可知,出现的小方格需顺时针旋转90°,向右平移至边界.
故选:C.
3.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1.则其旋转中心一定是( )
A.点E B.点F C.点G D.点H
【解答】解:根据旋转的性质,知:旋转中心,一定在对应点所连线段的垂直平分线上.
则其旋转中心是NN1和PP1的垂直平分线的交点,即点G.
故选:C.
4.如图,四边形AOBC绕点O顺时针方向旋转得到四边形DOEF,下列说法正确的是( )
A.旋转角是∠BOD
B.AO=EO
C.若连接CO,FO,则CO=FO
D.四边形AOBC和四边形DOEF可能不全等
【解答】解:∵四边形AOBC绕点O顺时针方向旋转得到四边形DOEF,
∴旋转角是∠AOD,OA=OD,四边形AOBC和四边形DOEF全等,故A、B、D选项错误;
若连接CO,FO,则CO=FO,故C选项正确,
故选:C.
5.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
【解答】解:现将数字“69”旋转180°,得到的数字是:69.
故选:B.
6.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转45° D.逆时针旋转45°
【解答】解:根据图形可知:将△ABC绕点A逆时针旋转90°可得到△ADE.
故选:B.
7.如图,P是等边三角形△ABC内的一点,连接PB、PC.若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )
A.45° B.60° C.90° D.120°
【解答】解:∵将△PBC绕点B旋转到△P′BA,
∴∠ABP′=∠CBP,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABP′+∠ABP=60°,
∴∠PBP′=60°,
故选:B.
8.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( )
A.M或O或N B.E或O或C C.E或O或N D.M或O或C
【解答】解:若以M为旋转中心,把正方形ABCD顺时针旋转90°,A点对应点为H,B点对应点为E,C点对应点为F,D点对应点为G,则可得到正方形EFGH;
若以O为旋转中心,把正方形ABCD旋转180°,A点对应点为G,B点对应点为H,C点对应点为E,D点对应点为F,则可得到正方形EFGH;
若以N为旋转中心,把正方形ABCD逆时针旋转90°,A点对应点为F,B点对应点为G,C点对应点为H,D点对应点为E,则可得到正方形EFGH.
故选:A.
9.如图,ABCD和DCGH是两块全等的正方形铁皮,要使它们重合,则存在的旋转中心有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:根据旋转的性质,可得要使正方形ABCD和DCGH重合,有3种方法,可以分别绕D、C或CD的中点旋转,
即旋转中心有3个.故选C.
二.填空题(共6小题)
10.如图,△CDE可以看成是△CAB绕某一点旋转后的图形.
(1)旋转中心是点 C ;
(2)点A、B、C的对应点分别依次是点 D、E、C ;
(3)∠A、∠B、∠ACB的对应角分别依次是 ∠D、∠E、∠DCE ;
(4)线段AC、BC、AB的对应线段分别依次是 DC、EC、DE ;
(5)旋转的角度是 ∠ACD的度数(或∠BCE的度数) .
【解答】解:(1)旋转中心是点C;
(2)点A、B、C的对应点分别依次是点D、E、C;
(3)∠A、∠B、∠ACB的对应角分别依次是∠D、∠E、∠DCE;
(4)线段AC、BC、AB的对应线段分别依次是DC、EC、DE;
(5)旋转的角度是∠ACD的度数(或∠BCE的度数).
故答案为:(1)C;(2)D、E、C;(3)∠D、∠E、∠DCE;(4)DC、EC、DE;(5)∠ACD的度数(或∠BCE的度数).
11.如图,△ABC是等腰三角形,∠BAC=80°,D为BC上一点,△ABD经过旋转至△ACE的位置.旋转角度是 80 度.
【解答】解:∵△ABD经过旋转至△ACE的位置,
∴旋转后AB对应AC,则旋转角等于∠BAC;
∵∠BAC=80°,
∴旋转角度是80°.
故答案为80.
12.如图,△ABC与△ADE都是直角三角形,∠B与∠AED都是直角,点E在AC上,∠D=30°,如果△ABC经过旋转后能与△AED重合,那么旋转中心是点 A ,逆时针旋转了 60 度.
【解答】解:根据题意,得
AC的对应边是AD,因此旋转的中心是点A,
旋转的度数是∠EAD的度数,即∠EAD的度数=90°﹣30°=60°.
故答案为A,60;
13.如图,等边三角形OAB绕点O顺时针旋转120°后得到△ODE,那么点B的对应点是 点E OA的对应线 OD ,∠B的对应角 ∠E ,旋转角是 ∠BOE 和 ∠AOD ,都等于 120° .
【解答】解:如图,∵等边三角形OAB绕点O顺时针旋转120°后得到△ODE,
∴△OAB≌△ODE,∠AOD=∠BOE=120°,
∴OB=OE,OA=OD,∠B=∠E,
∴点B的对应点是点E,OA的对应线OD,∠B的对应角∠E,旋转角是∠BOE和∠AOD,都等于120°.
故答案是:点E,OD,∠E,∠BOE和∠AOD,120°.
14.如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△ACE的位置,则旋转中心是 点C ;旋转角度是 90° ;点B的对应点是 点A ;点D的对应点是 点E ;线段CB的对应线段是 CA ;∠B的对应角是 ∠EAC ;如果点M是CB的,那么经过上述旋转后,点M移到了 点N处 .
【解答】解:根据图形分析可知,△CBD绕点C顺时针旋转90度后到达△ACE的位置,
故旋转中心是点C;
旋转角度是∠BCA=90°;
点B的对应点是点A;
点D的对应点是点E;
线段CB的对应点是CA;
∠B的对应角是∠EAC;
如果点M是CB的,那么经过上述旋转后,点M移到了点N处.
15.如图所示,将图形(1)以点O为旋转中心,每次旋转90°,则第2015次旋转后的图形是 (4) (在下列各图中选填正确图形的序号即可)
【解答】解:观察图形,将图形(1)以点O为旋转中心,每次顺时针旋转90°,得到下一个图形,每旋转四次回到原来的位置,
而2015=503×4+3,
所以第2015次旋转后的图形与(4)一样.
故答案为(4).
三.解答题(共6小题)
16.钟表的时针匀速旋转一周需要12小时,如图:
(1)指出它的旋转中心;
(2)经过5小时整,时针旋转了多少度?
【解答】解:(1)钟表圆盘的中心位置;
(2)∵钟表上的刻度把圆周12等分.
∴每一等分所对的圆心角是360°÷12=30°.
时针经过5小时整,需要旋转5格,即旋转角为30°×5=150°.
17.如图,△ABC是等腰三角形,∠BAC=40°,D是BC上一点,△ABD经过旋转后到达△ACE的位置,
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M在AB上,且AM=BM,那么经过上述旋转后,点M转到了什么位置?
【解答】解:(1)因为△ABD经旋转后到达△ACE,它们的公共顶点为A,所以旋转中心是点A;
(2)线段AB旋转后,对应边是AC,∠BAC就是旋转角,因为∠BAC=40°,所以旋转了40°;
(3)因为旋转前后AB,AC是对应边,故AB的中点M,旋转后就是AC的中点了,所以点M转到了AC的中点.
18.如图,△ABC是等边三角形,D是BC边上的中点,△ABD经过旋转后到达△ACE的位置,那么:
(1)旋转中心是点 A ;
(2)点B、D的对应点分别是点 C、E ;
(3)线段AB、BD、DA的对应线段分别是 线段AC、CE、EA ;
(4)∠B的对应角是 ∠ACE ;
(5)旋转角度为 60° ;
(6)△ACE的形状为 直角三角形 .
【解答】解:∵△ABD经过旋转后到达△ACE的位置,
∴(1)旋转中心是点A;
故答案为:A;
(2)点B、D的对应点分别是点C、E;
故答案为:点C、E;
(3)线段AB、BD、DA的对应线段分别是线段AC、CE、EA;
故答案为:线段AC、CE、EA;
(4)∠B的对应角是∠ACE;
故答案为:∠ACE;
(5)旋转角度为∠BAC=60°;
故答案为:60°;
(6)∵△ABC是等边三角形,D是BC边上的中点,
∴∠ADB=90°,
∴∠AEC=90°,
∴△ACE的形状为直角三角形.
故答案为:直角三角形.
19.如图所示,△ACD和△BCE都是等边三角形,△DCB经过旋转后得到△ACE.
(1)指出旋转中心是哪一点?
(2)旋转了多少度?
(3)图中还存在是旋转关系的三角形吗?
【解答】解:(1)∵△ACD和△BCE都是等边三角形,
∴CD=CA,CE=CB,∠ACD=∠BCE=60°,
∴△DCB绕点C逆时针旋转60°得到△ACE;
∴旋转中心为点C;
(2)旋转角为60°;
(3)△PCE绕点C顺时针旋转60°得到△QCB;△DCQ绕点C逆时针旋转60°得到△ACP.
20.如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
(1)点A的对应点是点 A′ ,线段AB的对应线段是 A′B′ ,∠D的对应角是 ∠D′ ;
(2)旋转中心是 点C ,∠BCB'的大小是 45° ,四边形A′B′CD′的形状是 长方形 ;
(3)在四边形A′B′CD′中与线段AD相等的线段有 A′D′、B′C .
【解答】解:(1)点A的对应点是点A',线段AB的对应线段是A'B',∠D的对应角是∠D';
(2)旋转中心是点C,∠BCB'的大小是45°,四边形A'B'CD'的形状是长方形;
(3)在四边形A'B'CD'中与线段AD相等的线段有A'D'、B'C.
21.如图,△ABE为等腰三角形,经旋转后得到△FDG,其中四边形ABCD为正方形,
试问:
(1)旋转中心为哪个点?
(2)旋转角为多少度?
(3)指出∠E的对应角及BE的对应边.
【解答】解:(1)如图所示:△ABE绕C点顺时针旋转90度,可得到△FDG,
即旋转中心为C点;
(2)△ABE绕C点顺时针旋转90度,可得到△FDG,
旋转角为90度;
(3)由(1)得:∠E的对应角为∠G,BE的对应边为DG.
第1页(共1页)
