10.1.1生活中的轴对称同步练习2021—2022学年华东师大版数学七年级下册
文档属性
| 名称 | 10.1.1生活中的轴对称同步练习2021—2022学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览



文档简介
10.1.1生活中的轴对称
★轴对称图形某个图形沿着一条直线对折,如果对折的两部分能够完全重合,那么这个图形称为轴对称图形,这条直线叫这个图形的对称轴
★两个图形成轴对称把一个图形沿着一条直线翻折过去,如果能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两图形重合时互相重合的点)叫做对称点
★轴对称图形的性质轴对称图形(或成轴对称的两个图形)的对应线段相等,对应角 相等.
一.选择题(共7小题)
1.下列不是轴对称图形的是( )
A. B. C. D.
2.如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条 B.3条 C.5条 D.无数条
3.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
4.新年伊始,虎年来临,大家都开始用上了虎的图腾与吉祥物.以下小老虎的表情设计没有利用轴对称的是( )
A. B.
C. D.
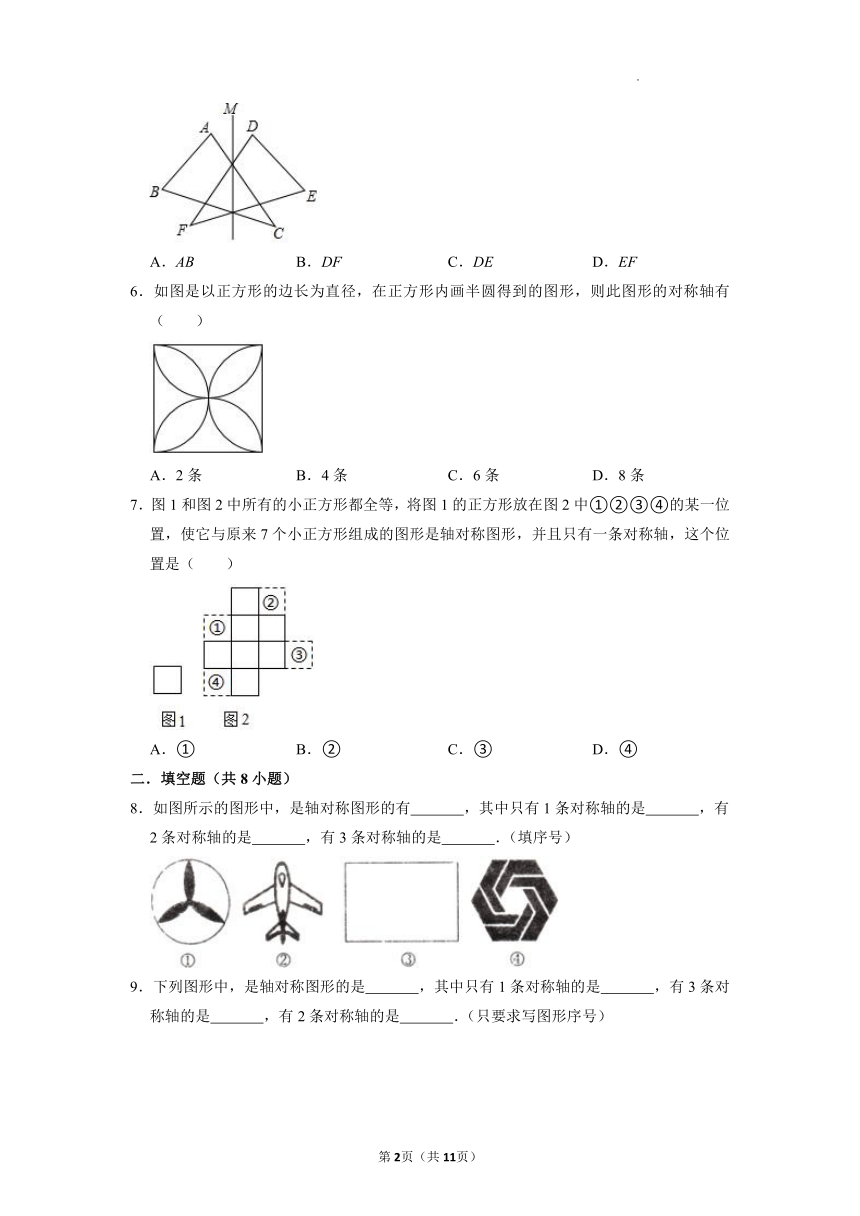
5.如图△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是( )
A.AB B.DF C.DE D.EF
6.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
7.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且只有一条对称轴,这个位置是( )
A.① B.② C.③ D.④
二.填空题(共8小题)
8.如图所示的图形中,是轴对称图形的有 ,其中只有1条对称轴的是 ,有2条对称轴的是 ,有3条对称轴的是 .(填序号)
9.下列图形中,是轴对称图形的是 ,其中只有1条对称轴的是 ,有3条对称轴的是 ,有2条对称轴的是 .(只要求写图形序号)
10.下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号)
11.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是 .
12.如图,△ABC和△A′B′C′关于直线m对称,∠C′=80°,∠A=50°,AB=a,B′C′=b,则∠C= ,∠B′= ,BC= ,A′B′= .
13.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为 度.
14.如图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm.则四边形ABCD的周长为 .
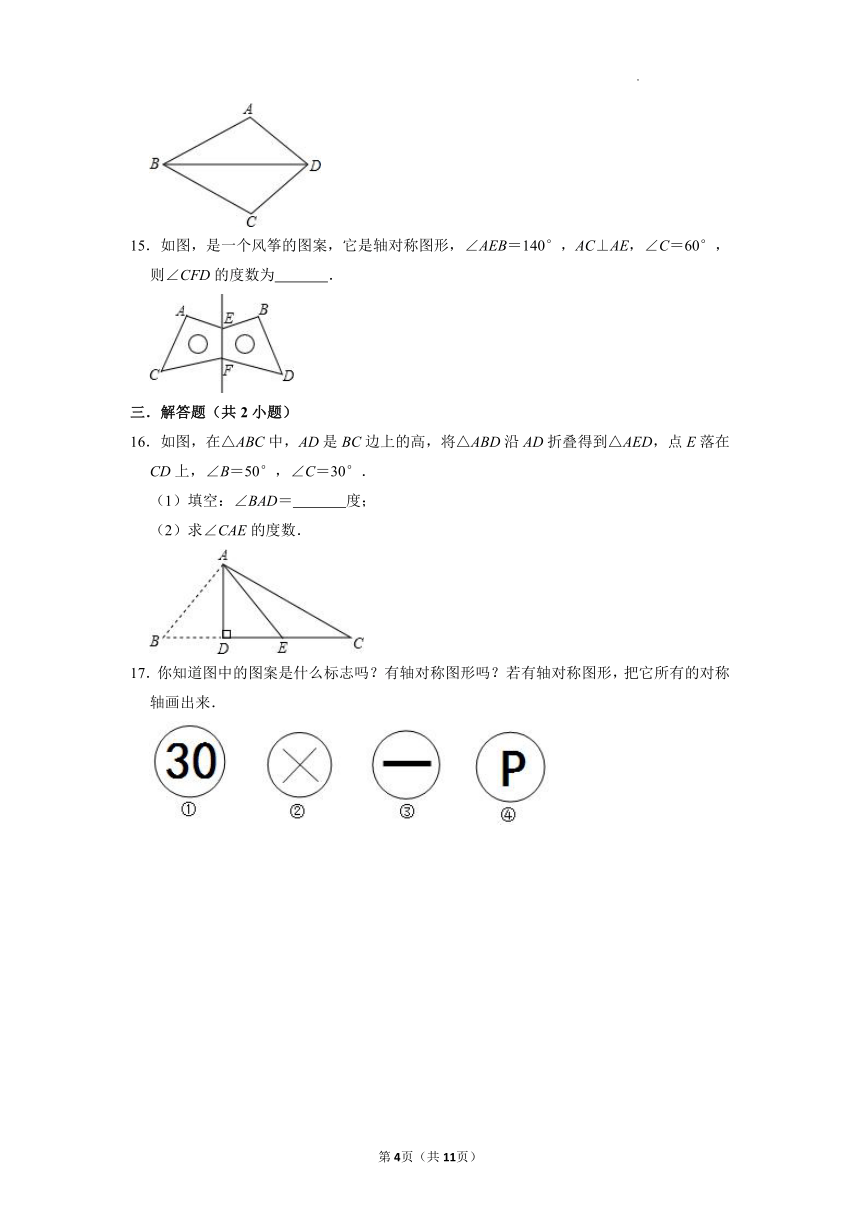
15.如图,是一个风筝的图案,它是轴对称图形,∠AEB=140°,AC⊥AE,∠C=60°,则∠CFD的度数为 .
三.解答题(共2小题)
16.如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 度;
(2)求∠CAE的度数.
17.你知道图中的图案是什么标志吗?有轴对称图形吗?若有轴对称图形,把它所有的对称轴画出来.
10.1.1生活中的轴对称
参考答案与试题解析
一.选择题(共7小题)
1.下列不是轴对称图形的是( )
A. B. C. D.
【解答】解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
2.如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条 B.3条 C.5条 D.无数条
【解答】解:五角星的对称轴共有5条,
故选:C.
3.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
【解答】解:选项B、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项A能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:A.
4.新年伊始,虎年来临,大家都开始用上了虎的图腾与吉祥物.以下小老虎的表情设计没有利用轴对称的是( )
A. B.
C. D.
【解答】解:根据对称轴两旁的部分能完全重合可知,B、C、D都利用了轴对称,A没有利用轴对称,
故选:A.
5.如图△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是( )
A.AB B.DF C.DE D.EF
【解答】解:∵△ABC与△DEF关于直线MN成轴对称,
∴AC=DF,
故选:B.
6.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
【解答】解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
所以此图形的对称轴有4条.
故选:B.
7.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且只有一条对称轴,这个位置是( )
A.① B.② C.③ D.④
【解答】解:A.是轴对称图形,但有两条对称轴,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.是轴对称图形,并且只有一条对称轴,故本选项符合题意;
D.不是轴对称图形,故本选项不合题意.
故选:C.
二.填空题(共8小题)
8.如图所示的图形中,是轴对称图形的有 ①②③ ,其中只有1条对称轴的是 ② ,有2条对称轴的是 ③ ,有3条对称轴的是 ① .(填序号)
【解答】解:是轴对称图形的有:①②③;
只有1条对称轴的是②,有2条对称轴的是③,有3条对称轴的①;
故答案为:①②③、②、③、①.
9.下列图形中,是轴对称图形的是 (1)(2)(3) ,其中只有1条对称轴的是 (1) ,有3条对称轴的是 (2) ,有2条对称轴的是 (3) .(只要求写图形序号)
【解答】解:是轴对称图形的是(1)(2)(3),其中只有1条对称轴的是(1),
有3条对称轴的是(2),有2条对称轴的是(3).
故答案为:(1)(2)(3),(1),(2),(3).
10.下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 ①②③④ (填序号)
【解答】解:根据轴对称图形的概念,可得出①②③④均为轴对称图形.
故答案为:①②③④.
11.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是 130° .
【解答】解:∵一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
∴∠D=40°,
∴∠BCD=360°﹣150°﹣40°﹣40°=130°.
故答案为:130°
12.如图,△ABC和△A′B′C′关于直线m对称,∠C′=80°,∠A=50°,AB=a,B′C′=b,则∠C= 80° ,∠B′= 50° ,BC= b ,A′B′= a .
【解答】解:如图,∵△ABC和△A′B′C′关于直线m对称,
∴∠C=∠C′,∠A=∠A′,∠B=∠B′.
又∵∠A+∠B+∠C=180°,∠C′=80°,∠A=50°,
∴∠C=∠C′=80°,∠B=∠B′=50°.
∵△ABC和△A′B′C′关于直线m对称,
∴AB=A′B′,BC=B′C′,
∵AB=a,B′C′=b,
∴A′B′=a,BC=b.
故答案是:80°;50°;b;a.
13.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为 54 度.
【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∵∠A=78°,∠C′=48°,
∴∠C=48°,
∴∠B=54°.
14.如图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm.则四边形ABCD的周长为 10.8cm .
【解答】解:∵四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm,
∴AB=BC=3.1cm,CD=AD=2.3cm,
则四边形ABCD的周长为:3.1+3.1+2.3+2.3=10.8(cm).
故答案为:10.8cm.
15.如图,是一个风筝的图案,它是轴对称图形,∠AEB=140°,AC⊥AE,∠C=60°,则∠CFD的度数为 160° .
【解答】解:∵EF为风筝的对称轴,
∴∠CFE=∠DFE,
∵∠AEB=140°,AC⊥AE,∠C=60°,
∴∠AEF=110°,
∴∠CFE=360°﹣90°﹣60°﹣110°=100°,
∴∠CFD=360°﹣2×100°=160°.
故答案为:160°.
三.解答题(共2小题)
16.如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 40 度;
(2)求∠CAE的度数.
【解答】解:(1)∵AD是BC边上的高,∠B=50°,
∴∠BAD=180°﹣90°﹣50°=40°.
故答案为:40;
(2)解法一:∵△AED是由△ABD折叠得到,
∴∠AED=∠B=50°,
∵∠AED是△ACE的外角,
∴∠AED=∠CAE+∠C,
∴∠CAE=∠AED﹣∠C=50°﹣30°=20°.
解法二:
∵△AED是由△ABD折叠得到,
∴∠EAD=∠BAD=40°,
∴∠BAE=80°,
∴∠CAE=180°﹣∠B﹣∠C﹣∠BAE=180°﹣50°﹣30°﹣80°=20°.
17.你知道图中的图案是什么标志吗?有轴对称图形吗?若有轴对称图形,把它所有的对称轴画出来.
【解答】解:如图所示:
①限速标志是轴对称图形,有1条对称轴;
②禁止停放标志是轴对称图形,有4条对称轴;
③禁止驶入标志是轴对称图形,有2条对称轴;
④停车场标志不是轴对称图形.
第1页(共1页)
★轴对称图形某个图形沿着一条直线对折,如果对折的两部分能够完全重合,那么这个图形称为轴对称图形,这条直线叫这个图形的对称轴
★两个图形成轴对称把一个图形沿着一条直线翻折过去,如果能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两图形重合时互相重合的点)叫做对称点
★轴对称图形的性质轴对称图形(或成轴对称的两个图形)的对应线段相等,对应角 相等.
一.选择题(共7小题)
1.下列不是轴对称图形的是( )
A. B. C. D.
2.如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条 B.3条 C.5条 D.无数条
3.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
4.新年伊始,虎年来临,大家都开始用上了虎的图腾与吉祥物.以下小老虎的表情设计没有利用轴对称的是( )
A. B.
C. D.
5.如图△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是( )
A.AB B.DF C.DE D.EF
6.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
7.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且只有一条对称轴,这个位置是( )
A.① B.② C.③ D.④
二.填空题(共8小题)
8.如图所示的图形中,是轴对称图形的有 ,其中只有1条对称轴的是 ,有2条对称轴的是 ,有3条对称轴的是 .(填序号)
9.下列图形中,是轴对称图形的是 ,其中只有1条对称轴的是 ,有3条对称轴的是 ,有2条对称轴的是 .(只要求写图形序号)
10.下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 (填序号)
11.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是 .
12.如图,△ABC和△A′B′C′关于直线m对称,∠C′=80°,∠A=50°,AB=a,B′C′=b,则∠C= ,∠B′= ,BC= ,A′B′= .
13.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为 度.
14.如图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm.则四边形ABCD的周长为 .
15.如图,是一个风筝的图案,它是轴对称图形,∠AEB=140°,AC⊥AE,∠C=60°,则∠CFD的度数为 .
三.解答题(共2小题)
16.如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 度;
(2)求∠CAE的度数.
17.你知道图中的图案是什么标志吗?有轴对称图形吗?若有轴对称图形,把它所有的对称轴画出来.
10.1.1生活中的轴对称
参考答案与试题解析
一.选择题(共7小题)
1.下列不是轴对称图形的是( )
A. B. C. D.
【解答】解:选项A、C、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
2.如图所示的五角星是轴对称图形,它的对称轴共有( )
A.1条 B.3条 C.5条 D.无数条
【解答】解:五角星的对称轴共有5条,
故选:C.
3.在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
【解答】解:选项B、C、D不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项A能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:A.
4.新年伊始,虎年来临,大家都开始用上了虎的图腾与吉祥物.以下小老虎的表情设计没有利用轴对称的是( )
A. B.
C. D.
【解答】解:根据对称轴两旁的部分能完全重合可知,B、C、D都利用了轴对称,A没有利用轴对称,
故选:A.
5.如图△ABC与△DEF关于直线MN成轴对称,那么线段AC的对应线段是( )
A.AB B.DF C.DE D.EF
【解答】解:∵△ABC与△DEF关于直线MN成轴对称,
∴AC=DF,
故选:B.
6.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
【解答】解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
所以此图形的对称轴有4条.
故选:B.
7.图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且只有一条对称轴,这个位置是( )
A.① B.② C.③ D.④
【解答】解:A.是轴对称图形,但有两条对称轴,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.是轴对称图形,并且只有一条对称轴,故本选项符合题意;
D.不是轴对称图形,故本选项不合题意.
故选:C.
二.填空题(共8小题)
8.如图所示的图形中,是轴对称图形的有 ①②③ ,其中只有1条对称轴的是 ② ,有2条对称轴的是 ③ ,有3条对称轴的是 ① .(填序号)
【解答】解:是轴对称图形的有:①②③;
只有1条对称轴的是②,有2条对称轴的是③,有3条对称轴的①;
故答案为:①②③、②、③、①.
9.下列图形中,是轴对称图形的是 (1)(2)(3) ,其中只有1条对称轴的是 (1) ,有3条对称轴的是 (2) ,有2条对称轴的是 (3) .(只要求写图形序号)
【解答】解:是轴对称图形的是(1)(2)(3),其中只有1条对称轴的是(1),
有3条对称轴的是(2),有2条对称轴的是(3).
故答案为:(1)(2)(3),(1),(2),(3).
10.下列图标是由我们熟悉的一些基本数学图形组成的,其中是轴对称图形的是 ①②③④ (填序号)
【解答】解:根据轴对称图形的概念,可得出①②③④均为轴对称图形.
故答案为:①②③④.
11.如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是 130° .
【解答】解:∵一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
∴∠D=40°,
∴∠BCD=360°﹣150°﹣40°﹣40°=130°.
故答案为:130°
12.如图,△ABC和△A′B′C′关于直线m对称,∠C′=80°,∠A=50°,AB=a,B′C′=b,则∠C= 80° ,∠B′= 50° ,BC= b ,A′B′= a .
【解答】解:如图,∵△ABC和△A′B′C′关于直线m对称,
∴∠C=∠C′,∠A=∠A′,∠B=∠B′.
又∵∠A+∠B+∠C=180°,∠C′=80°,∠A=50°,
∴∠C=∠C′=80°,∠B=∠B′=50°.
∵△ABC和△A′B′C′关于直线m对称,
∴AB=A′B′,BC=B′C′,
∵AB=a,B′C′=b,
∴A′B′=a,BC=b.
故答案是:80°;50°;b;a.
13.如图,△ABC与△A′B′C′关于直线l对称,且∠A=78°,∠C′=48°,则∠B的度数为 54 度.
【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∵∠A=78°,∠C′=48°,
∴∠C=48°,
∴∠B=54°.
14.如图,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm.则四边形ABCD的周长为 10.8cm .
【解答】解:∵四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=3.1cm,CD=2.3cm,
∴AB=BC=3.1cm,CD=AD=2.3cm,
则四边形ABCD的周长为:3.1+3.1+2.3+2.3=10.8(cm).
故答案为:10.8cm.
15.如图,是一个风筝的图案,它是轴对称图形,∠AEB=140°,AC⊥AE,∠C=60°,则∠CFD的度数为 160° .
【解答】解:∵EF为风筝的对称轴,
∴∠CFE=∠DFE,
∵∠AEB=140°,AC⊥AE,∠C=60°,
∴∠AEF=110°,
∴∠CFE=360°﹣90°﹣60°﹣110°=100°,
∴∠CFD=360°﹣2×100°=160°.
故答案为:160°.
三.解答题(共2小题)
16.如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
(1)填空:∠BAD= 40 度;
(2)求∠CAE的度数.
【解答】解:(1)∵AD是BC边上的高,∠B=50°,
∴∠BAD=180°﹣90°﹣50°=40°.
故答案为:40;
(2)解法一:∵△AED是由△ABD折叠得到,
∴∠AED=∠B=50°,
∵∠AED是△ACE的外角,
∴∠AED=∠CAE+∠C,
∴∠CAE=∠AED﹣∠C=50°﹣30°=20°.
解法二:
∵△AED是由△ABD折叠得到,
∴∠EAD=∠BAD=40°,
∴∠BAE=80°,
∴∠CAE=180°﹣∠B﹣∠C﹣∠BAE=180°﹣50°﹣30°﹣80°=20°.
17.你知道图中的图案是什么标志吗?有轴对称图形吗?若有轴对称图形,把它所有的对称轴画出来.
【解答】解:如图所示:
①限速标志是轴对称图形,有1条对称轴;
②禁止停放标志是轴对称图形,有4条对称轴;
③禁止驶入标志是轴对称图形,有2条对称轴;
④停车场标志不是轴对称图形.
第1页(共1页)
