10.1.2轴对称的再认识同步练习2021—2022学年华东师大版数学七年级下册
文档属性
| 名称 | 10.1.2轴对称的再认识同步练习2021—2022学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 174.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 15:35:21 | ||
图片预览


文档简介
10.1.2轴对称的再认识
★经过线段 中点且 垂直 于这条线段的直线,叫做这条线段的垂直平分线。
★线段是轴对称图形,它的对称轴是它的垂 平分线和线段所在的直线
★角是轴对称图形,它的对称轴是角平分线所在的直线
★如果一个图形是输对称图形,耶么连结对称点的线段的 垂直平分线就是该图形的对称轴
★轴对称图形的对称轴的画法
(1)找任意一组对称点,连结对称点;
(2)画出对称点所连线段的垂直平分线.
★作对称轴的“三字诀”:
(1)找:无论是作成轴对称的两个图形的对称轴,还是作轴对称图形的对称轴,其关键都是找出图形中的任意一对对称点;
(2)连:连结这对对称点;
(3)作:作所连线段的垂直平分线,该垂直平分线就是这两个成轴对称的图形或这个轴对称图形的一条对称轴
★在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等
一.选择题(共9小题)
1.下列轴对称图形中,只用一把无刻度的直尺不能画出对称轴的是( )
A.正方形 B.正五边形 C.等腰梯形 D.等腰三角形
2.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
3.下列说法正确的是( )
A.线段有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
4.下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
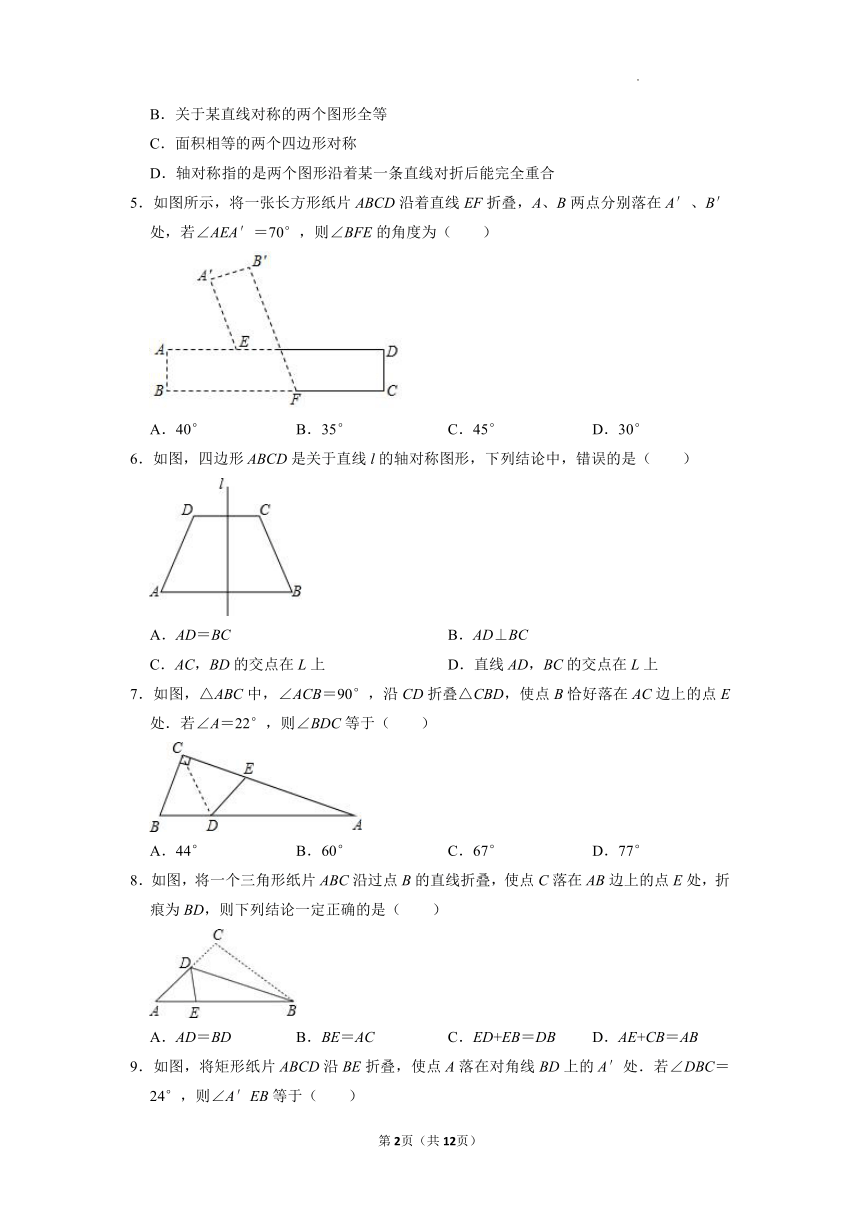
5.如图所示,将一张长方形纸片ABCD沿着直线EF折叠,A、B两点分别落在A′、B′处,若∠AEA′=70°,则∠BFE的角度为( )
A.40° B.35° C.45° D.30°
6.如图,四边形ABCD是关于直线l的轴对称图形,下列结论中,错误的是( )
A.AD=BC B.AD⊥BC
C.AC,BD的交点在L上 D.直线AD,BC的交点在L上
7.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A.44° B.60° C.67° D.77°
8.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.BE=AC C.ED+EB=DB D.AE+CB=AB
9.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A′处.若∠DBC=24°,则∠A′EB等于( )
A.24° B.33° C.57° D.66°
二.填空题(共4小题)
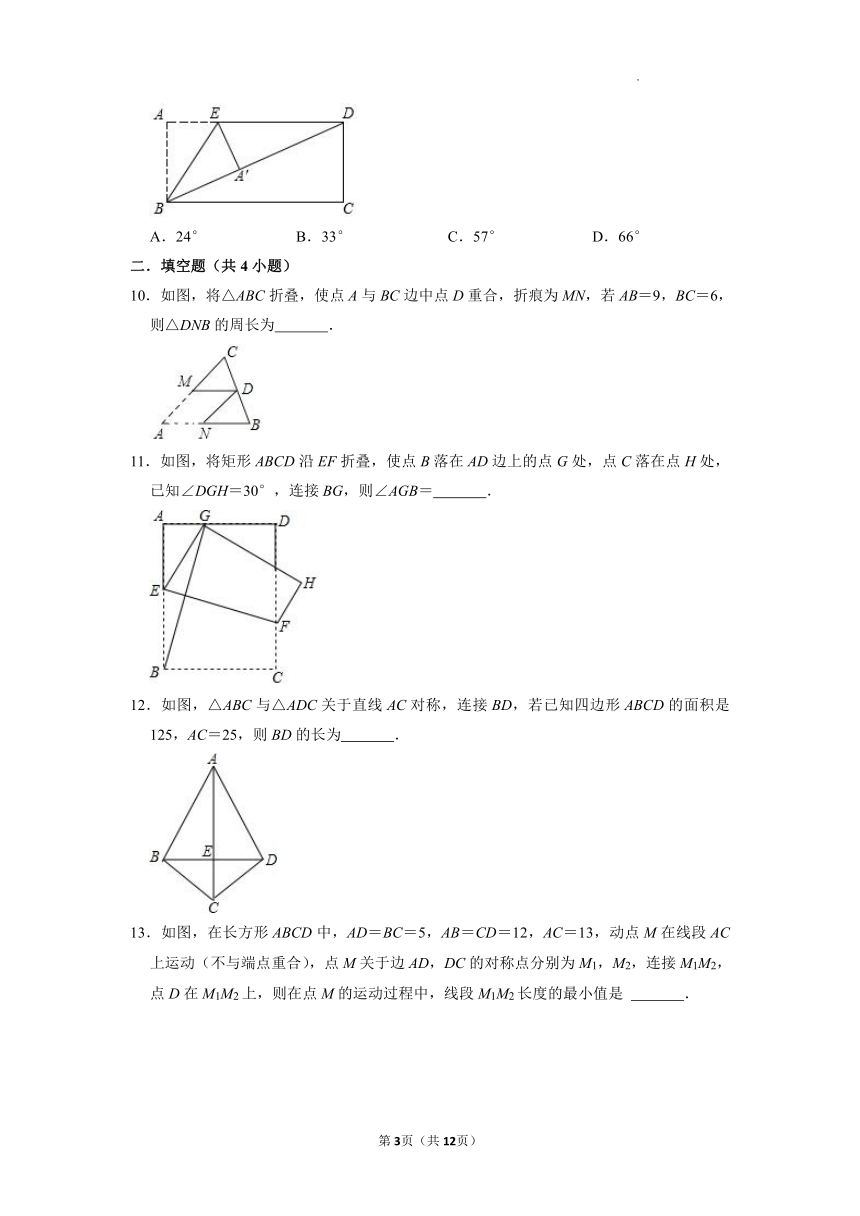
10.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为 .
11.如图,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处,已知∠DGH=30°,连接BG,则∠AGB= .
12.如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 .
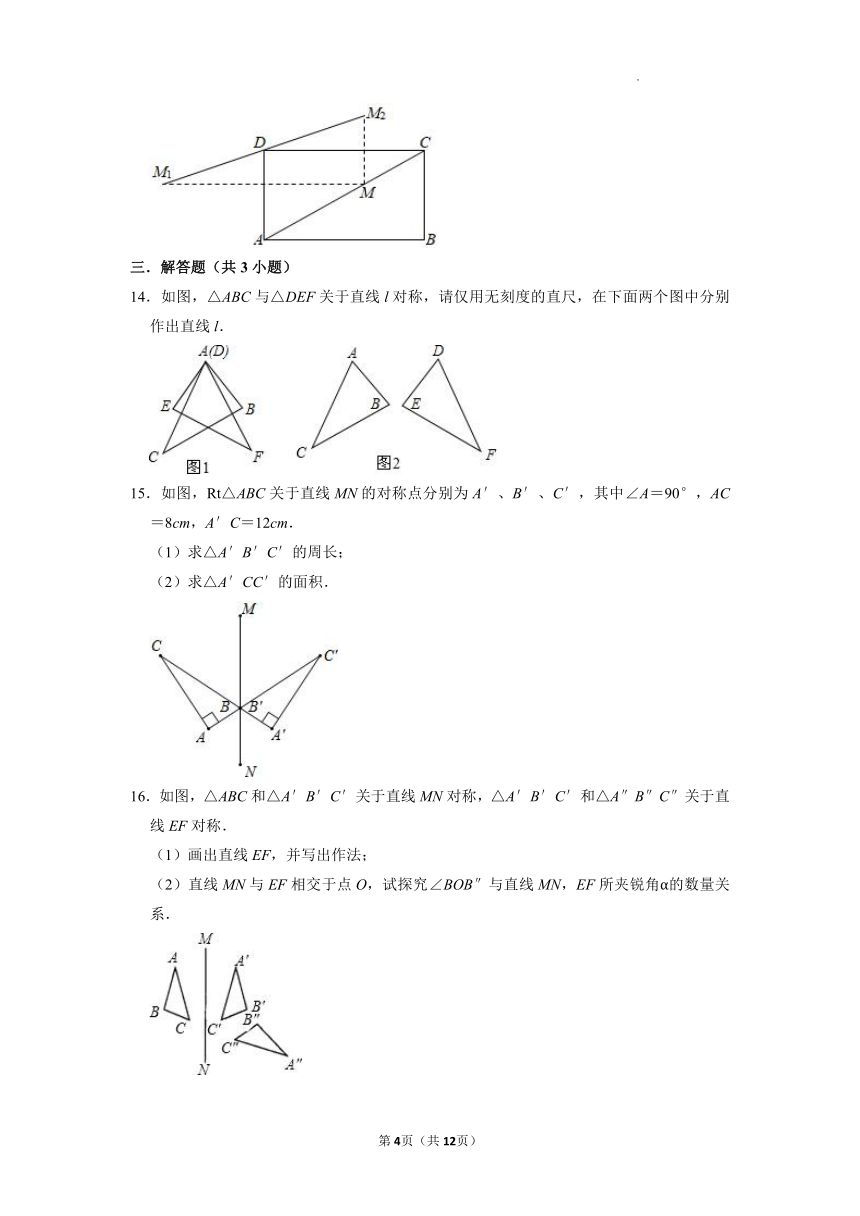
13.如图,在长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是 .
三.解答题(共3小题)
14.如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
15.如图,Rt△ABC关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8cm,A′C=12cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
16.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF,并写出作法;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
10.1.2轴对称的再认识
参考答案与试题解析
一.选择题(共9小题)
1.下列轴对称图形中,只用一把无刻度的直尺不能画出对称轴的是( )
A.正方形 B.正五边形 C.等腰梯形 D.等腰三角形
【解答】解:A、正方形,对角线所在的直线即为对称轴,可以用直尺画出,故A选项错误;
B、正五边形,作一条对角线把正五边形分成一等腰三角形与以等腰梯形,根据正五边形的对称性,过等腰三角形的顶点与梯形的对角线的交点的直线即为对称轴,故B选项错误;
C、等腰梯形,延长两腰相交于一点,作两对角线相交于一点,根据等腰梯形的对称性,过这两点的直线即为对称轴,故C选项错误;
D、等腰三角形,只用一把无刻度的直尺无法画出,故D选项正确.
故选:D.
2.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
【解答】解:∵△ABC与△A'B'C'关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=OB′,
故选项A,C,D正确,
故选:B.
3.下列说法正确的是( )
A.线段有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
【解答】解:A、根据线段有两条对称轴,故此选项错误;
B、根据垂直平分线段的直线就是线段的对称轴,故此选项错误;
C、根据角的对称轴是角的平分线所在直线,故此选项错误;
D、根据角平分线所在的直线是角的对称轴,故此选项正确;
故选:D.
4.下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
【解答】解:A、B、D都正确;
C、面积相等的两个四边形不一定全等,故不一定轴对称,错误.
故选:C.
5.如图所示,将一张长方形纸片ABCD沿着直线EF折叠,A、B两点分别落在A′、B′处,若∠AEA′=70°,则∠BFE的角度为( )
A.40° B.35° C.45° D.30°
【解答】解:
由平行线的性质得,∠AEA'=∠1=70°,
∵AD∥BC,
∴∠1=∠BFB'=70°,
由折叠性质得,∠BFE=∠EFB'=∠BFB'=35°,
故选:B.
6.如图,四边形ABCD是关于直线l的轴对称图形,下列结论中,错误的是( )
A.AD=BC B.AD⊥BC
C.AC,BD的交点在L上 D.直线AD,BC的交点在L上
【解答】解:A、四边形ABCD是关于直线L的轴对称图形,必有AD=BC,正确;
B、AD、BC与L的夹角相等,但不一定垂直,错误;
C、AC,BD的交点在L上,正确;
D、直线AD,BC的交点在L上,正确.
故选:B.
7.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A.44° B.60° C.67° D.77°
【解答】解:△ABC中,∠ACB=90°,∠A=22°,
∴∠B=90°﹣∠A=68°,
由折叠的性质可得:∠CED=∠B=68°,∠BDC=∠EDC,
∴∠ADE=∠CED﹣∠A=46°,
∴∠BDC==67°.
故选:C.
8.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.BE=AC C.ED+EB=DB D.AE+CB=AB
【解答】解析:∵△BDE是由△BDC翻折而成,
∴BE=BC,
∵AE+BE=AB,
∴AE+CB=AB,
故D正确,
无法得出AD=CD,AE=AD,AD=DE,
故选:D.
9.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A′处.若∠DBC=24°,则∠A′EB等于( )
A.24° B.33° C.57° D.66°
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD∥BC,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∵AD∥BC,
∴∠ADB=∠DBC=24°,
∴∠A'BE=∠ABE=(90°﹣∠ADB)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
二.填空题(共4小题)
10.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为 12 .
【解答】解:∵D为BC的中点,且BC=6,
∴BD=BC=3,
由折叠性质知NA=ND,
则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,
故答案为:12.
11.如图,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处,已知∠DGH=30°,连接BG,则∠AGB= 75° .
【解答】解:由折叠的性质可知:GE=BE,∠EGH=∠ABC=90°,
∴∠EBG=∠EGB.
∴∠EGH﹣∠EGB=∠EBC﹣∠EBG,即:∠GBC=∠BGH.
又∵AD∥BC,
∴∠AGB=∠GBC.
∴∠AGB=∠BGH.
∵∠DGH=30°,
∴∠AGH=150°,
∴∠AGB=∠AGH=75°,
故答案为:75°.
12.如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 10 .
【解答】解:∵△ABC与△ADC关于直线AC对称,
∴△ABC与△ADC的面积相等;
四边形ABCD的面积等于△ABC与△ADC的面积之和;
四边形ABCD的面积=AC×BD=125
AC=25,
则BD=10.
13.如图,在长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是 .
【解答】解:过D作DM'⊥AC于M',连接DM,如图:
长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,
∴S△ADC=AD CD=AC DM',
∴DM'==,
∵M关于边AD,DC的对称点分别为M1,M2,
∴DM1=DM=DM2,
∴M1M2=2DM,
线段M1M2长度最小即是DM长度最小,此时DM⊥AC,即M与M'重合,M1M2最小值为2DM'=.
故答案为:.
三.解答题(共3小题)
14.如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
【解答】解:如图所示.
15.如图,Rt△ABC关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8cm,A′C=12cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
【解答】解:(1)∵Rt△ABC关于直线MN的对称点分别为A′、B′、C′,AC=8cm,A′C=12cm,
∴AB=A′B′,BC=B′C′,
∴△A′B′C′的周长为:A′C′+B′C′+A′B′=A′C+AC=12+8=20(cm);
(2)由(1)得:△A′CC′的面积为:A′C×A′C′=×12×8=48(cm2).
16.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF,并写出作法;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
【解答】解:(1)
作法:连接B′B″,作线段B′B″的垂直平分线EF.
(2)连接B′O,
则α=∠MOB′+∠B′OE,∠BOB″=∠BOM+∠MOB′+∠B′OE+∠EOB″.
又因为△ABC与△A′B′C′关于直线MN对称,
△A′B′C′与△A″B″C″关于直线EF对称,
所以∠BOM=∠MOB′,∠B′OE=∠EOB″,
所以∠BOB″=2∠MOB′+2∠B′OE,
所以∠BOB″=2α.
第1页(共1页)
★经过线段 中点且 垂直 于这条线段的直线,叫做这条线段的垂直平分线。
★线段是轴对称图形,它的对称轴是它的垂 平分线和线段所在的直线
★角是轴对称图形,它的对称轴是角平分线所在的直线
★如果一个图形是输对称图形,耶么连结对称点的线段的 垂直平分线就是该图形的对称轴
★轴对称图形的对称轴的画法
(1)找任意一组对称点,连结对称点;
(2)画出对称点所连线段的垂直平分线.
★作对称轴的“三字诀”:
(1)找:无论是作成轴对称的两个图形的对称轴,还是作轴对称图形的对称轴,其关键都是找出图形中的任意一对对称点;
(2)连:连结这对对称点;
(3)作:作所连线段的垂直平分线,该垂直平分线就是这两个成轴对称的图形或这个轴对称图形的一条对称轴
★在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等
一.选择题(共9小题)
1.下列轴对称图形中,只用一把无刻度的直尺不能画出对称轴的是( )
A.正方形 B.正五边形 C.等腰梯形 D.等腰三角形
2.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
3.下列说法正确的是( )
A.线段有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
4.下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
5.如图所示,将一张长方形纸片ABCD沿着直线EF折叠,A、B两点分别落在A′、B′处,若∠AEA′=70°,则∠BFE的角度为( )
A.40° B.35° C.45° D.30°
6.如图,四边形ABCD是关于直线l的轴对称图形,下列结论中,错误的是( )
A.AD=BC B.AD⊥BC
C.AC,BD的交点在L上 D.直线AD,BC的交点在L上
7.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A.44° B.60° C.67° D.77°
8.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.BE=AC C.ED+EB=DB D.AE+CB=AB
9.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A′处.若∠DBC=24°,则∠A′EB等于( )
A.24° B.33° C.57° D.66°
二.填空题(共4小题)
10.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为 .
11.如图,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处,已知∠DGH=30°,连接BG,则∠AGB= .
12.如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 .
13.如图,在长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是 .
三.解答题(共3小题)
14.如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
15.如图,Rt△ABC关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8cm,A′C=12cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
16.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF,并写出作法;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
10.1.2轴对称的再认识
参考答案与试题解析
一.选择题(共9小题)
1.下列轴对称图形中,只用一把无刻度的直尺不能画出对称轴的是( )
A.正方形 B.正五边形 C.等腰梯形 D.等腰三角形
【解答】解:A、正方形,对角线所在的直线即为对称轴,可以用直尺画出,故A选项错误;
B、正五边形,作一条对角线把正五边形分成一等腰三角形与以等腰梯形,根据正五边形的对称性,过等腰三角形的顶点与梯形的对角线的交点的直线即为对称轴,故B选项错误;
C、等腰梯形,延长两腰相交于一点,作两对角线相交于一点,根据等腰梯形的对称性,过这两点的直线即为对称轴,故C选项错误;
D、等腰三角形,只用一把无刻度的直尺无法画出,故D选项正确.
故选:D.
2.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
【解答】解:∵△ABC与△A'B'C'关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=OB′,
故选项A,C,D正确,
故选:B.
3.下列说法正确的是( )
A.线段有且只有一条对称轴
B.垂直于线段的直线就是线段的对称轴
C.角的对称轴是角的平分线
D.角平分线所在的直线是角的对称轴
【解答】解:A、根据线段有两条对称轴,故此选项错误;
B、根据垂直平分线段的直线就是线段的对称轴,故此选项错误;
C、根据角的对称轴是角的平分线所在直线,故此选项错误;
D、根据角平分线所在的直线是角的对称轴,故此选项正确;
故选:D.
4.下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个四边形对称
D.轴对称指的是两个图形沿着某一条直线对折后能完全重合
【解答】解:A、B、D都正确;
C、面积相等的两个四边形不一定全等,故不一定轴对称,错误.
故选:C.
5.如图所示,将一张长方形纸片ABCD沿着直线EF折叠,A、B两点分别落在A′、B′处,若∠AEA′=70°,则∠BFE的角度为( )
A.40° B.35° C.45° D.30°
【解答】解:
由平行线的性质得,∠AEA'=∠1=70°,
∵AD∥BC,
∴∠1=∠BFB'=70°,
由折叠性质得,∠BFE=∠EFB'=∠BFB'=35°,
故选:B.
6.如图,四边形ABCD是关于直线l的轴对称图形,下列结论中,错误的是( )
A.AD=BC B.AD⊥BC
C.AC,BD的交点在L上 D.直线AD,BC的交点在L上
【解答】解:A、四边形ABCD是关于直线L的轴对称图形,必有AD=BC,正确;
B、AD、BC与L的夹角相等,但不一定垂直,错误;
C、AC,BD的交点在L上,正确;
D、直线AD,BC的交点在L上,正确.
故选:B.
7.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A.44° B.60° C.67° D.77°
【解答】解:△ABC中,∠ACB=90°,∠A=22°,
∴∠B=90°﹣∠A=68°,
由折叠的性质可得:∠CED=∠B=68°,∠BDC=∠EDC,
∴∠ADE=∠CED﹣∠A=46°,
∴∠BDC==67°.
故选:C.
8.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.BE=AC C.ED+EB=DB D.AE+CB=AB
【解答】解析:∵△BDE是由△BDC翻折而成,
∴BE=BC,
∵AE+BE=AB,
∴AE+CB=AB,
故D正确,
无法得出AD=CD,AE=AD,AD=DE,
故选:D.
9.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A′处.若∠DBC=24°,则∠A′EB等于( )
A.24° B.33° C.57° D.66°
【解答】解:∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD∥BC,
由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,
∵AD∥BC,
∴∠ADB=∠DBC=24°,
∴∠A'BE=∠ABE=(90°﹣∠ADB)=(90°﹣24°)=33°,
∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°.
故选:C.
二.填空题(共4小题)
10.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为 12 .
【解答】解:∵D为BC的中点,且BC=6,
∴BD=BC=3,
由折叠性质知NA=ND,
则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,
故答案为:12.
11.如图,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处,已知∠DGH=30°,连接BG,则∠AGB= 75° .
【解答】解:由折叠的性质可知:GE=BE,∠EGH=∠ABC=90°,
∴∠EBG=∠EGB.
∴∠EGH﹣∠EGB=∠EBC﹣∠EBG,即:∠GBC=∠BGH.
又∵AD∥BC,
∴∠AGB=∠GBC.
∴∠AGB=∠BGH.
∵∠DGH=30°,
∴∠AGH=150°,
∴∠AGB=∠AGH=75°,
故答案为:75°.
12.如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 10 .
【解答】解:∵△ABC与△ADC关于直线AC对称,
∴△ABC与△ADC的面积相等;
四边形ABCD的面积等于△ABC与△ADC的面积之和;
四边形ABCD的面积=AC×BD=125
AC=25,
则BD=10.
13.如图,在长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,动点M在线段AC上运动(不与端点重合),点M关于边AD,DC的对称点分别为M1,M2,连接M1M2,点D在M1M2上,则在点M的运动过程中,线段M1M2长度的最小值是 .
【解答】解:过D作DM'⊥AC于M',连接DM,如图:
长方形ABCD中,AD=BC=5,AB=CD=12,AC=13,
∴S△ADC=AD CD=AC DM',
∴DM'==,
∵M关于边AD,DC的对称点分别为M1,M2,
∴DM1=DM=DM2,
∴M1M2=2DM,
线段M1M2长度最小即是DM长度最小,此时DM⊥AC,即M与M'重合,M1M2最小值为2DM'=.
故答案为:.
三.解答题(共3小题)
14.如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
【解答】解:如图所示.
15.如图,Rt△ABC关于直线MN的对称点分别为A′、B′、C′,其中∠A=90°,AC=8cm,A′C=12cm.
(1)求△A′B′C′的周长;
(2)求△A′CC′的面积.
【解答】解:(1)∵Rt△ABC关于直线MN的对称点分别为A′、B′、C′,AC=8cm,A′C=12cm,
∴AB=A′B′,BC=B′C′,
∴△A′B′C′的周长为:A′C′+B′C′+A′B′=A′C+AC=12+8=20(cm);
(2)由(1)得:△A′CC′的面积为:A′C×A′C′=×12×8=48(cm2).
16.如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF,并写出作法;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN,EF所夹锐角α的数量关系.
【解答】解:(1)
作法:连接B′B″,作线段B′B″的垂直平分线EF.
(2)连接B′O,
则α=∠MOB′+∠B′OE,∠BOB″=∠BOM+∠MOB′+∠B′OE+∠EOB″.
又因为△ABC与△A′B′C′关于直线MN对称,
△A′B′C′与△A″B″C″关于直线EF对称,
所以∠BOM=∠MOB′,∠B′OE=∠EOB″,
所以∠BOB″=2∠MOB′+2∠B′OE,
所以∠BOB″=2α.
第1页(共1页)
