2021—2022学年华东师大版数学七年级下册 10.1.3画轴对称图形 同步练习(word版含解析)
文档属性
| 名称 | 2021—2022学年华东师大版数学七年级下册 10.1.3画轴对称图形 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览


文档简介
10.1.3画轴对称图形
★能按要求作出简单平面图形经过轴对称后的图形.
★画轴对称图形的基本步骤
(1)找特殊点(线段端点、角的顶点等);
(2)作特殊点关于直线 l 的对称点;
(3)连结所作各点得出轴对称图形.
注意:从图形上找到关键的顶点,分别向对称轴引垂线,并延长找到对称点,顺次连结.
★画一个图形关于某条直线对称的图形需要注意:(1)图形上的特殊点即有角的顶点,线段的端点等:(2)对称轴上的点的对称点是它本身;(3)找图形上的特殊点时,要找全,否则画出的对称图形不准确.
★镜子内的图形与物体成轴对称关系,关于竖直的一条直线对称.根据镜子中的像与实际时刻轴对称的规律,只要在右边画一条直线作为对称轴,然后画出各数字的对称图形即可.
一.选择题(共6小题)
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A. B.
C. D.
2.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1 B.2 C.3 D.4
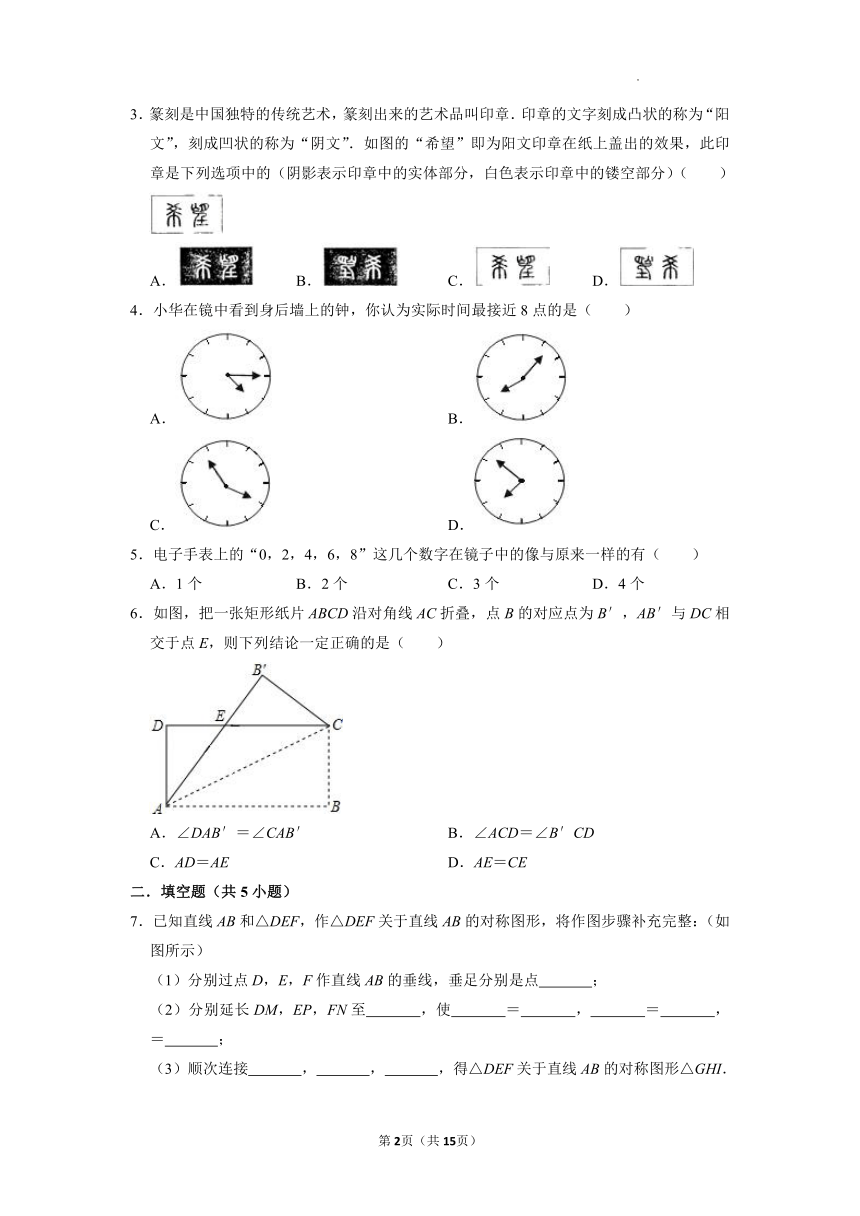
3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )
A. B. C. D.
4.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是( )
A. B.
C. D.
5.电子手表上的“0,2,4,6,8”这几个数字在镜子中的像与原来一样的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD
C.AD=AE D.AE=CE
二.填空题(共5小题)
7.已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:(如图所示)
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点 ;
(2)分别延长DM,EP,FN至 ,使 = , = , = ;
(3)顺次连接 , , ,得△DEF关于直线AB的对称图形△GHI.
8.一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 .
9.如图所示,有一个英语单词,四个字母都关于直线l对称,请依据轴对称的知识,写出这个单词所指的物品 .
10.在张纸上写着一窜数,其在镜子中形状如图,则纸上写的数字为 .
11.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
三.解答题(共7小题)
12.如图,已知△ABC.
(1)画出△ABC关于直线AC对称的△A1C1B1(不要求写画法);
(2)若∠BAC=35°,∠B=20°,求∠BCB1的大小.
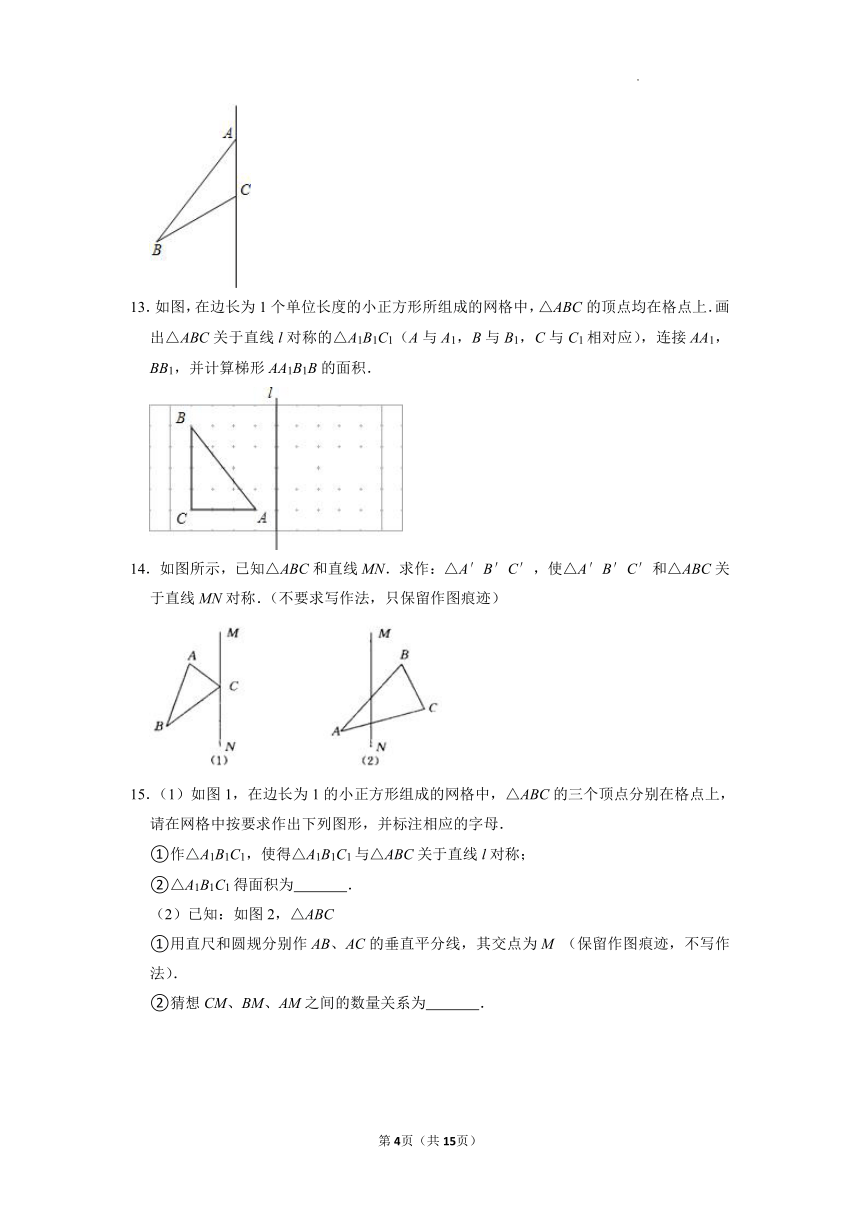
13.如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应),连接AA1,BB1,并计算梯形AA1B1B的面积.
14.如图所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
15.(1)如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
①作△A1B1C1,使得△A1B1C1与△ABC关于直线l对称;
②△A1B1C1得面积为 .
(2)已知:如图2,△ABC
①用直尺和圆规分别作AB、AC的垂直平分线,其交点为M (保留作图痕迹,不写作法).
②猜想CM、BM、AM之间的数量关系为 .
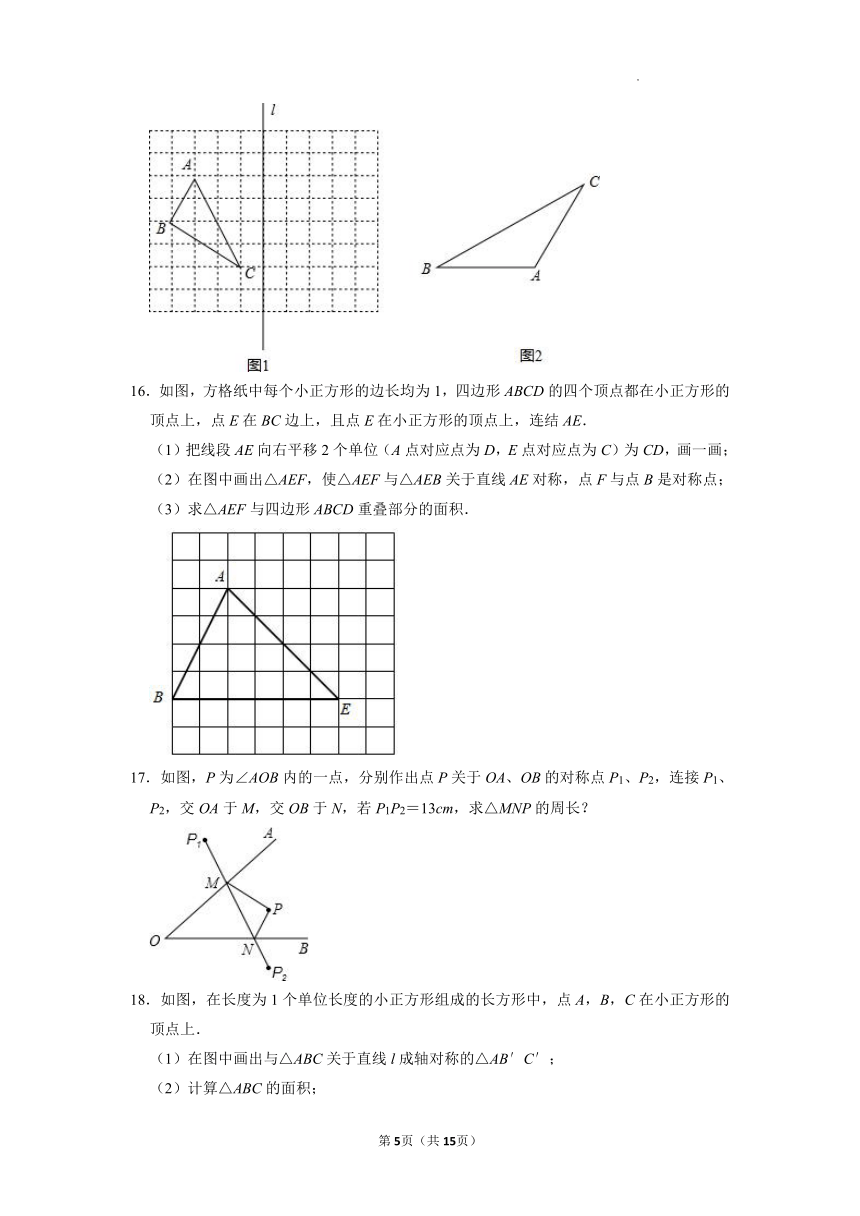
16.如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连结AE.
(1)把线段AE向右平移2个单位(A点对应点为D,E点对应点为C)为CD,画一画;
(2)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(3)求△AEF与四边形ABCD重叠部分的面积.
17.如图,P为∠AOB内的一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,若P1P2=13cm,求△MNP的周长?
18.如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
10.1.3画轴对称图形
参考答案与试题解析
一.选择题(共6小题)
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A. B.
C. D.
【解答】解:作△ABC关于直线MN的轴对称图形正确的是B选项,
故选:B.
2.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1 B.2 C.3 D.4
【解答】解:根据轴对称的性质可知,台球走过的路径为:
∴该球最后将落入的球袋是4号.
故选:D.
3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )
A. B. C. D.
【解答】解:易得“望”字应在左边,字以外的部分为镂空部分,故选D.
4.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是( )
A. B.
C. D.
【解答】解:实际时间为8点的时针关于过12时、6时的直线的对称点是4点,
那么8点的时钟在镜子中看来应该是4点的样子.
故选:C.
5.电子手表上的“0,2,4,6,8”这几个数字在镜子中的像与原来一样的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:电子手表上的“0,2,4,6,8”这几个数字在镜子中的像与原来一样的有“0,8”共2个,故选B.
6.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD
C.AD=AE D.AE=CE
【解答】解:∵矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,
∴∠BAC=∠CAB′,
∵AB∥CD,
∴∠BAC=∠ACD,
∴∠ACD=∠CAB′,
∴AE=CE,
所以,结论正确的是D选项.
故选:D.
二.填空题(共5小题)
7.已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:(如图所示)
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点 M,P,N ;
(2)分别延长DM,EP,FN至 点G,H,I ,使 MG = DM , PH = EP , NI = FN ;
(3)顺次连接 GH , HI , IG ,得△DEF关于直线AB的对称图形△GHI.
【解答】解:依据轴对称的性质得:
(1)M,P,N;
(2)点G,H,L
MG=DMPH=EPNL=FN;
(3)GH,HL,LG.
8.一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 BA629 .
【解答】解:关于镜面对称,也可以看成是关于某条直线对称,
∴关于某条直线对称的数字依次是BA629.
故答案为BA629.
9.如图所示,有一个英语单词,四个字母都关于直线l对称,请依据轴对称的知识,写出这个单词所指的物品 书 .
【解答】解:根据轴对称的知识,这个单词是book,
这个单词所指的物品是书,
故答案为:书
10.在张纸上写着一窜数,其在镜子中形状如图,则纸上写的数字为 21518 .
【解答】解:由图分析可得题中所给的“81215”与“21518”成轴对称,这时的时间应是21518.
故本题答案为:21518.
11.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 3 cm.
【解答】解:将△ADE沿直线DE折叠,点A落在点A′处,
所以AD=A′D,AE=A′E.
则阴影部分图形的周长等于BC+BD+CE+A′D+A′E,
=BC+BD+CE+AD+AE,
=BC+AB+AC,
=3cm.
故答案为:3.
三.解答题(共7小题)
12.如图,已知△ABC.
(1)画出△ABC关于直线AC对称的△A1C1B1(不要求写画法);
(2)若∠BAC=35°,∠B=20°,求∠BCB1的大小.
【解答】解:(1)所画图形如下所示:
(2)∵∠BCO=∠BAC+∠B=55°,
∴∠BCB1=2∠BCO=110°.
13.如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应),连接AA1,BB1,并计算梯形AA1B1B的面积.
【解答】解:△A1B1C1如图所示,
梯形AA1B1B的面积=×(2+8)×4=20.
14.如图所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
【解答】解:
不限定用尺规作图.
画第(1)个图(2),
画第(2)个图(3),
写出结论(1).
15.(1)如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
①作△A1B1C1,使得△A1B1C1与△ABC关于直线l对称;
②△A1B1C1得面积为 4 .
(2)已知:如图2,△ABC
①用直尺和圆规分别作AB、AC的垂直平分线,其交点为M (保留作图痕迹,不写作法).
②猜想CM、BM、AM之间的数量关系为 AM=BM=CM .
【解答】解:(1)①如图1所示:
②△A1B1C1得面积:3×4﹣×2×4﹣×2×1﹣×2×3=4,
故答案为:4;
(2)①如图2所示:
②连接BM、AM、CM,
∵MN是AB的垂直平分线,
∴MA=MB,
∵ME是AC的垂直平分线,
∴MA=MC,
∴AM=BM=CM,
故答案为:AM=BM=CM.
16.如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连结AE.
(1)把线段AE向右平移2个单位(A点对应点为D,E点对应点为C)为CD,画一画;
(2)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(3)求△AEF与四边形ABCD重叠部分的面积.
【解答】解:(1)如图,CD为所作;
(2)如图,△AEF为所作;
(3)△AEF与四边形ABCD重叠部分的面积=×6×4﹣×2×4﹣×2×2=6.
17.如图,P为∠AOB内的一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,若P1P2=13cm,求△MNP的周长?
【解答】解:∵点P关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△MNP的周长等于P1P2=13cm.
18.如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
【解答】解:(1)△AB′C′如图所示;
(2)△ABC的面积=3×4﹣×2×3﹣×1×4﹣×1×3,
=12﹣3﹣2﹣1.5,
=12﹣6.5,
=5.5;
(3)点P如图所示.
第1页(共1页)
★能按要求作出简单平面图形经过轴对称后的图形.
★画轴对称图形的基本步骤
(1)找特殊点(线段端点、角的顶点等);
(2)作特殊点关于直线 l 的对称点;
(3)连结所作各点得出轴对称图形.
注意:从图形上找到关键的顶点,分别向对称轴引垂线,并延长找到对称点,顺次连结.
★画一个图形关于某条直线对称的图形需要注意:(1)图形上的特殊点即有角的顶点,线段的端点等:(2)对称轴上的点的对称点是它本身;(3)找图形上的特殊点时,要找全,否则画出的对称图形不准确.
★镜子内的图形与物体成轴对称关系,关于竖直的一条直线对称.根据镜子中的像与实际时刻轴对称的规律,只要在右边画一条直线作为对称轴,然后画出各数字的对称图形即可.
一.选择题(共6小题)
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A. B.
C. D.
2.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1 B.2 C.3 D.4
3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )
A. B. C. D.
4.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是( )
A. B.
C. D.
5.电子手表上的“0,2,4,6,8”这几个数字在镜子中的像与原来一样的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD
C.AD=AE D.AE=CE
二.填空题(共5小题)
7.已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:(如图所示)
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点 ;
(2)分别延长DM,EP,FN至 ,使 = , = , = ;
(3)顺次连接 , , ,得△DEF关于直线AB的对称图形△GHI.
8.一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 .
9.如图所示,有一个英语单词,四个字母都关于直线l对称,请依据轴对称的知识,写出这个单词所指的物品 .
10.在张纸上写着一窜数,其在镜子中形状如图,则纸上写的数字为 .
11.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 cm.
三.解答题(共7小题)
12.如图,已知△ABC.
(1)画出△ABC关于直线AC对称的△A1C1B1(不要求写画法);
(2)若∠BAC=35°,∠B=20°,求∠BCB1的大小.
13.如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应),连接AA1,BB1,并计算梯形AA1B1B的面积.
14.如图所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
15.(1)如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
①作△A1B1C1,使得△A1B1C1与△ABC关于直线l对称;
②△A1B1C1得面积为 .
(2)已知:如图2,△ABC
①用直尺和圆规分别作AB、AC的垂直平分线,其交点为M (保留作图痕迹,不写作法).
②猜想CM、BM、AM之间的数量关系为 .
16.如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连结AE.
(1)把线段AE向右平移2个单位(A点对应点为D,E点对应点为C)为CD,画一画;
(2)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(3)求△AEF与四边形ABCD重叠部分的面积.
17.如图,P为∠AOB内的一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,若P1P2=13cm,求△MNP的周长?
18.如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
10.1.3画轴对称图形
参考答案与试题解析
一.选择题(共6小题)
1.下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
A. B.
C. D.
【解答】解:作△ABC关于直线MN的轴对称图形正确的是B选项,
故选:B.
2.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1 B.2 C.3 D.4
【解答】解:根据轴对称的性质可知,台球走过的路径为:
∴该球最后将落入的球袋是4号.
故选:D.
3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )
A. B. C. D.
【解答】解:易得“望”字应在左边,字以外的部分为镂空部分,故选D.
4.小华在镜中看到身后墙上的钟,你认为实际时间最接近8点的是( )
A. B.
C. D.
【解答】解:实际时间为8点的时针关于过12时、6时的直线的对称点是4点,
那么8点的时钟在镜子中看来应该是4点的样子.
故选:C.
5.电子手表上的“0,2,4,6,8”这几个数字在镜子中的像与原来一样的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:电子手表上的“0,2,4,6,8”这几个数字在镜子中的像与原来一样的有“0,8”共2个,故选B.
6.如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD
C.AD=AE D.AE=CE
【解答】解:∵矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,
∴∠BAC=∠CAB′,
∵AB∥CD,
∴∠BAC=∠ACD,
∴∠ACD=∠CAB′,
∴AE=CE,
所以,结论正确的是D选项.
故选:D.
二.填空题(共5小题)
7.已知直线AB和△DEF,作△DEF关于直线AB的对称图形,将作图步骤补充完整:(如图所示)
(1)分别过点D,E,F作直线AB的垂线,垂足分别是点 M,P,N ;
(2)分别延长DM,EP,FN至 点G,H,I ,使 MG = DM , PH = EP , NI = FN ;
(3)顺次连接 GH , HI , IG ,得△DEF关于直线AB的对称图形△GHI.
【解答】解:依据轴对称的性质得:
(1)M,P,N;
(2)点G,H,L
MG=DMPH=EPNL=FN;
(3)GH,HL,LG.
8.一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是 BA629 .
【解答】解:关于镜面对称,也可以看成是关于某条直线对称,
∴关于某条直线对称的数字依次是BA629.
故答案为BA629.
9.如图所示,有一个英语单词,四个字母都关于直线l对称,请依据轴对称的知识,写出这个单词所指的物品 书 .
【解答】解:根据轴对称的知识,这个单词是book,
这个单词所指的物品是书,
故答案为:书
10.在张纸上写着一窜数,其在镜子中形状如图,则纸上写的数字为 21518 .
【解答】解:由图分析可得题中所给的“81215”与“21518”成轴对称,这时的时间应是21518.
故本题答案为:21518.
11.如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为 3 cm.
【解答】解:将△ADE沿直线DE折叠,点A落在点A′处,
所以AD=A′D,AE=A′E.
则阴影部分图形的周长等于BC+BD+CE+A′D+A′E,
=BC+BD+CE+AD+AE,
=BC+AB+AC,
=3cm.
故答案为:3.
三.解答题(共7小题)
12.如图,已知△ABC.
(1)画出△ABC关于直线AC对称的△A1C1B1(不要求写画法);
(2)若∠BAC=35°,∠B=20°,求∠BCB1的大小.
【解答】解:(1)所画图形如下所示:
(2)∵∠BCO=∠BAC+∠B=55°,
∴∠BCB1=2∠BCO=110°.
13.如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应),连接AA1,BB1,并计算梯形AA1B1B的面积.
【解答】解:△A1B1C1如图所示,
梯形AA1B1B的面积=×(2+8)×4=20.
14.如图所示,已知△ABC和直线MN.求作:△A′B′C′,使△A′B′C′和△ABC关于直线MN对称.(不要求写作法,只保留作图痕迹)
【解答】解:
不限定用尺规作图.
画第(1)个图(2),
画第(2)个图(3),
写出结论(1).
15.(1)如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
①作△A1B1C1,使得△A1B1C1与△ABC关于直线l对称;
②△A1B1C1得面积为 4 .
(2)已知:如图2,△ABC
①用直尺和圆规分别作AB、AC的垂直平分线,其交点为M (保留作图痕迹,不写作法).
②猜想CM、BM、AM之间的数量关系为 AM=BM=CM .
【解答】解:(1)①如图1所示:
②△A1B1C1得面积:3×4﹣×2×4﹣×2×1﹣×2×3=4,
故答案为:4;
(2)①如图2所示:
②连接BM、AM、CM,
∵MN是AB的垂直平分线,
∴MA=MB,
∵ME是AC的垂直平分线,
∴MA=MC,
∴AM=BM=CM,
故答案为:AM=BM=CM.
16.如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连结AE.
(1)把线段AE向右平移2个单位(A点对应点为D,E点对应点为C)为CD,画一画;
(2)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(3)求△AEF与四边形ABCD重叠部分的面积.
【解答】解:(1)如图,CD为所作;
(2)如图,△AEF为所作;
(3)△AEF与四边形ABCD重叠部分的面积=×6×4﹣×2×4﹣×2×2=6.
17.如图,P为∠AOB内的一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,若P1P2=13cm,求△MNP的周长?
【解答】解:∵点P关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△MNP的周长等于P1P2=13cm.
18.如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
【解答】解:(1)△AB′C′如图所示;
(2)△ABC的面积=3×4﹣×2×3﹣×1×4﹣×1×3,
=12﹣3﹣2﹣1.5,
=12﹣6.5,
=5.5;
(3)点P如图所示.
第1页(共1页)
