10.2.2平移的特征同步练习2021—2022学年华东师大版数学七年级下册
文档属性
| 名称 | 10.2.2平移的特征同步练习2021—2022学年华东师大版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 214.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 15:39:59 | ||
图片预览



文档简介
10.2.2平移的特征
★平移后的图形与原来图形的对应线段平行并且相等,对应角相等,图形的形状与大小不变
★平移后对应点所连的线段平行(或在同一条直线上)并且相等
★平移作图的两种基本方法
(1)作出一条对应点所连的线段后,再作出以另外一些对应点为端点,与已作线段平行且相等的线段,再连结作出的线段的另一端;
(2)作出平移前的图形的一些对应线段,得出平移后的图形.
平移作图时,找关键点的对应点是十分重要的一步。平移作图的一般步骤为:
①先确定平移的方向和距离,即确定一组对应点;
②确定图形中的关键点;
利用第一组对应点和平移的性质确定图中所有关键点的对应点;
④按原图形顺序依次连结对应点,所得到的图形即为平移后的图形.
一.选择题(共8小题)
1.如图,△ABC经过平移到△DEF的位置,则下列四个“说法”中正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④BC∥EF,BC=EF
A.1个 B.2个 C.3个 D.4个
2.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
3.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
4.如图所示,是两个重叠的直角三角形,将其中的△ABC沿着BC方向平移BE的长得到△DEF,已知AB=8,BE=5,DH=3,则CF的长是( )
A.4 B.5 C.3 D.无法确定
5.如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16 cm B.18 cm C.20 cm D.21 cm
6.如图,矩形ABCD经过平移后成为矩形EFGH,矩形长AD和宽AB分别为6和4,图中DE=5,那么矩形ABCD平移的距离为( )
A.11 B.10 C.6 D.4
7.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是( )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1=2S2
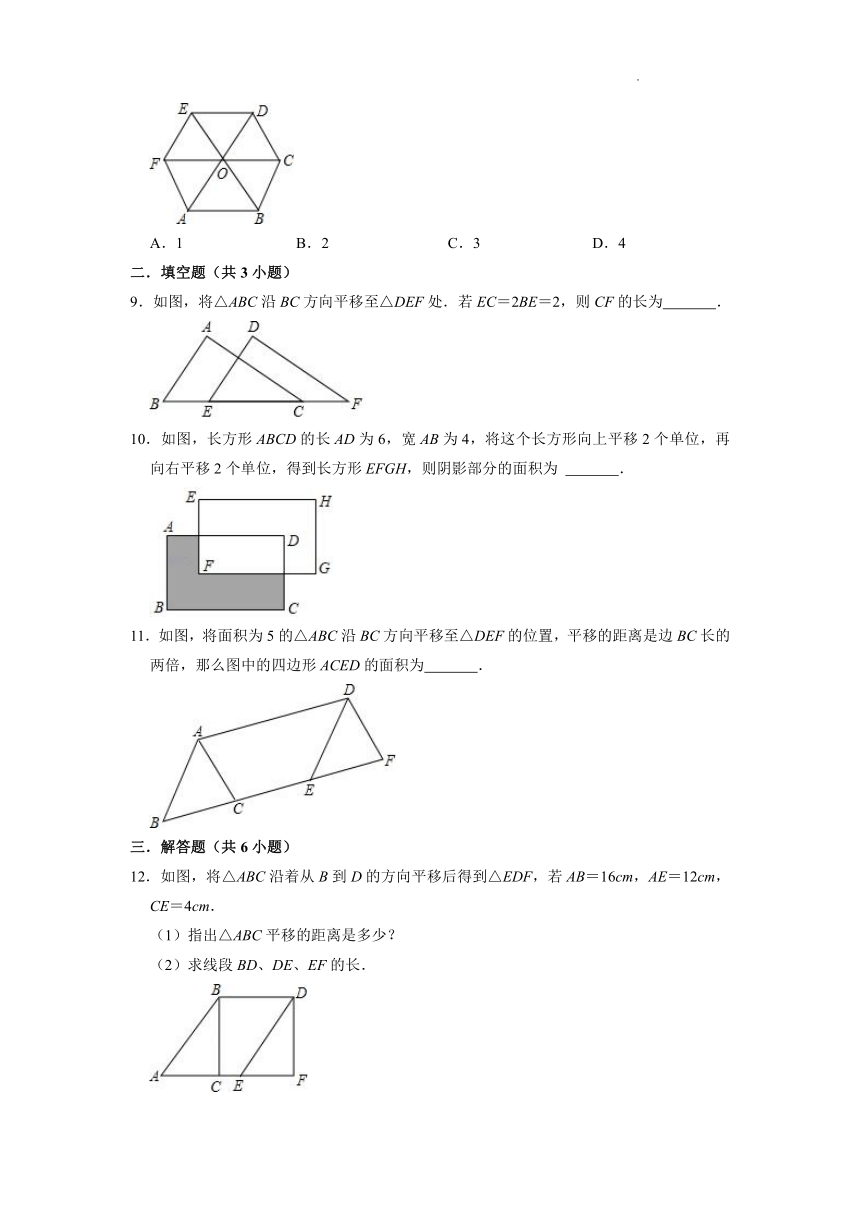
8.如图,O是正六边形ABCDEF的中心,在这个正六边形中,可以由△OBC平移得到的三角形的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共3小题)
9.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为 .
10.如图,长方形ABCD的长AD为6,宽AB为4,将这个长方形向上平移2个单位,再向右平移2个单位,得到长方形EFGH,则阴影部分的面积为 .
11.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .
三.解答题(共6小题)
12.如图,将△ABC沿着从B到D的方向平移后得到△EDF,若AB=16cm,AE=12cm,CE=4cm.
(1)指出△ABC平移的距离是多少?
(2)求线段BD、DE、EF的长.
13.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
14.如图,在边长为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点C移到了点C′的位置.
(1)画出平移后的△A′B′C′(点A′与点A对应,点B′与点B对应)
(2)指出平移的方向和平移的距离.
15.顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△A2B2C2;
(3)在(1)中△ABC向上平移过程中,边AC所扫过区域的面积是 .
16.如图:将四边形ABCD进行平移后,使点A的对应点为点A′,请你画出平移后所得的四边形A′B′C′D′(画图工具不限).
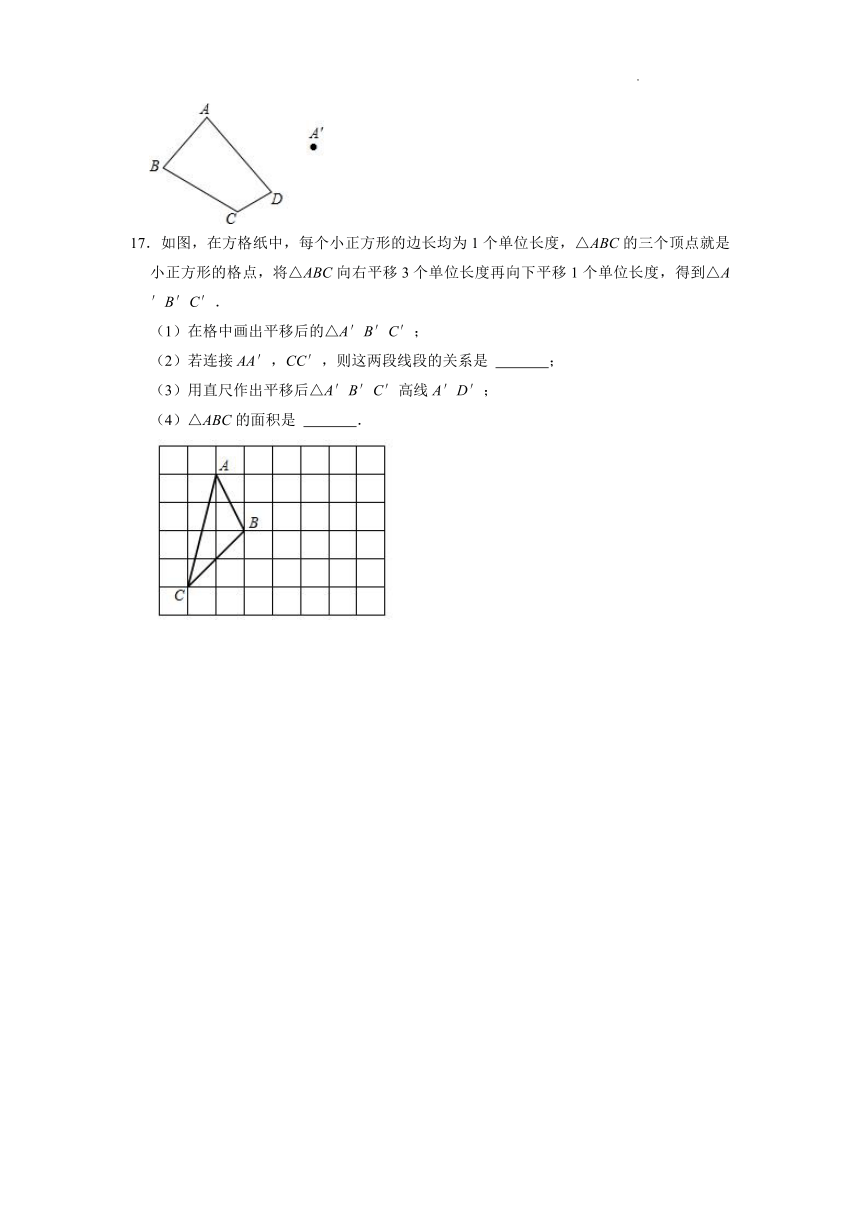
17.如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 .
10.2.2平移的特征
参考答案与试题解析
一.选择题(共8小题)
1.如图,△ABC经过平移到△DEF的位置,则下列四个“说法”中正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④BC∥EF,BC=EF
A.1个 B.2个 C.3个 D.4个
【解答】解:①根据平移的性质可知AB∥DE,AB=DE正确;
②根据平移的性质可AD∥BE∥CF,AD=BE=CF正确;
③根据平移的性质可知AC∥DF,AC=DF正确;
④根据平移的性质可知BC∥EF,BC=EF正确.
故正确有个数有四个.
故选:D.
2.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
【解答】解:在四边形EFGH,EH是AD的对应边,∠F是∠B的对应角,
∵AD=5,∠B=70°,故EH=5,∠F=70°.
故选:B.
3.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
【解答】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
故选:A.
4.如图所示,是两个重叠的直角三角形,将其中的△ABC沿着BC方向平移BE的长得到△DEF,已知AB=8,BE=5,DH=3,则CF的长是( )
A.4 B.5 C.3 D.无法确定
【解答】解:根据平移的性质,
易得CF=BE=5,
故选:B.
5.如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16 cm B.18 cm C.20 cm D.21 cm
【解答】解:∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴四边形ABFD的周长=AB+BE+DF+AD+EF,
=AB+BE+AE+AD+EF,
=△ABE的周长+AD+EF,
∵平移距离为2cm,
∴AD=EF=2cm,
∵△ABE的周长是16cm,
∴四边形ABFD的周长=16+2+2=20cm.
故选:C.
6.如图,矩形ABCD经过平移后成为矩形EFGH,矩形长AD和宽AB分别为6和4,图中DE=5,那么矩形ABCD平移的距离为( )
A.11 B.10 C.6 D.4
【解答】解:由图可知,对应点A、E间的距离为平移距离,
∵AD=6,DE=5,
∴AE=AD+DE=6+5=11.
故选:A.
7.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是( )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1=2S2
【解答】解:
∵△ABC沿着BC方向平移得到△A′B′C′,
∴AA′∥BC′,
∵点P是直线AA′上任意一点,
∴△ABC,△PB′C′的高相等,
∴S1=S2,
故选:C.
8.如图,O是正六边形ABCDEF的中心,在这个正六边形中,可以由△OBC平移得到的三角形的个数是( )
A.1 B.2 C.3 D.4
【解答】解:△COD方向发生了变化,不属于平移得到;
△EOD形状和大小没有变化,属于平移得到;
△EOF方向发生了变化,不属于平移得到;
△FAO形状和大小没有变化,属于平移得到;
△ABO方向发生了变化,不属于平移得到.
∴可以由△OBC平移得到的是△EOD,△FAO.
故正确的有2个.
故选:B.
二.填空题(共3小题)
9.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为 1 .
【解答】解:∵△ABC沿BC方向平移至△DEF处.
∴BE=CF,
∵EC=2BE=2,
∴BE=1,
∴CF=1.
故答案为1.
10.如图,长方形ABCD的长AD为6,宽AB为4,将这个长方形向上平移2个单位,再向右平移2个单位,得到长方形EFGH,则阴影部分的面积为 16 .
【解答】解:过点F作FN⊥BC于N,
由平移可得:AM=2,FN=2,
∴MD=AD﹣AM=6﹣2=4,MF=AB﹣FN=4﹣2=2,
∴阴影部分的面积=S矩形ABCD﹣S矩形MFQD=4×6﹣2×4=16,
故答案为:16.
11.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 15 .
【解答】解:设点A到BC的距离为h,则S△ABC=BC h=5,
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积=(AD+CE) h=(2BC+BC) h=3×BC h=3×5=15.
故答案为:15.
三.解答题(共6小题)
12.如图,将△ABC沿着从B到D的方向平移后得到△EDF,若AB=16cm,AE=12cm,CE=4cm.
(1)指出△ABC平移的距离是多少?
(2)求线段BD、DE、EF的长.
【解答】解:(1)∵AE=12cm,
∴平移的距离=AE=12cm;
(2)∵三角形ABC沿着从B到D的方向平移后得到三角形EDF,
∴BD=AE=12cm,DE=AB=16cm,EF=AC=AE﹣CE=16﹣4=8cm.
13.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= 6 cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
【解答】解:(1)∵将△ABC沿直线AB向右平移得到△BDE,
∴△ABC≌△BDE,
∴BE=AC=6cm,
故答案为:6;
(2)由(1)知△ABC≌△BDE,
∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,
∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.
14.如图,在边长为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点C移到了点C′的位置.
(1)画出平移后的△A′B′C′(点A′与点A对应,点B′与点B对应)
(2)指出平移的方向和平移的距离.
【解答】解:(1)如图所示:△A′B′C′即为所求;
(2)如图连接CC′,平移方向是点C到点C′的方向,
平移距离为:CC′==.
15.顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△A2B2C2;
(3)在(1)中△ABC向上平移过程中,边AC所扫过区域的面积是 8 .
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图所示:△AB2C2即为所求;
(3)∵△ABC向上平移4个单位后得到的△A1B1C1,△ABC向上平移过程中,边AC所扫过区域是以4为边长,以2为高的平行四边形,
∴边AC所扫过区域的面积=4×2=8.
故答案为:8.
16.如图:将四边形ABCD进行平移后,使点A的对应点为点A′,请你画出平移后所得的四边形A′B′C′D′(画图工具不限).
【解答】解:
分别画四条平行线各(1分),共(4分),
连接四个顶点(2分).
17.如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 平行且相等. ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 3 .
【解答】解:(1)如图,△A′B′C′即为所求.
(2)如图,AA′∥CC′.
故答案为:平行且相等.
(3)如图,线段A′D′即为所求.
(4)△ABC的面积=2×4﹣×1×4﹣×1×2﹣×2×2=3,
故答案为:3.
★平移后的图形与原来图形的对应线段平行并且相等,对应角相等,图形的形状与大小不变
★平移后对应点所连的线段平行(或在同一条直线上)并且相等
★平移作图的两种基本方法
(1)作出一条对应点所连的线段后,再作出以另外一些对应点为端点,与已作线段平行且相等的线段,再连结作出的线段的另一端;
(2)作出平移前的图形的一些对应线段,得出平移后的图形.
平移作图时,找关键点的对应点是十分重要的一步。平移作图的一般步骤为:
①先确定平移的方向和距离,即确定一组对应点;
②确定图形中的关键点;
利用第一组对应点和平移的性质确定图中所有关键点的对应点;
④按原图形顺序依次连结对应点,所得到的图形即为平移后的图形.
一.选择题(共8小题)
1.如图,△ABC经过平移到△DEF的位置,则下列四个“说法”中正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④BC∥EF,BC=EF
A.1个 B.2个 C.3个 D.4个
2.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
3.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
4.如图所示,是两个重叠的直角三角形,将其中的△ABC沿着BC方向平移BE的长得到△DEF,已知AB=8,BE=5,DH=3,则CF的长是( )
A.4 B.5 C.3 D.无法确定
5.如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16 cm B.18 cm C.20 cm D.21 cm
6.如图,矩形ABCD经过平移后成为矩形EFGH,矩形长AD和宽AB分别为6和4,图中DE=5,那么矩形ABCD平移的距离为( )
A.11 B.10 C.6 D.4
7.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是( )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1=2S2
8.如图,O是正六边形ABCDEF的中心,在这个正六边形中,可以由△OBC平移得到的三角形的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共3小题)
9.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为 .
10.如图,长方形ABCD的长AD为6,宽AB为4,将这个长方形向上平移2个单位,再向右平移2个单位,得到长方形EFGH,则阴影部分的面积为 .
11.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .
三.解答题(共6小题)
12.如图,将△ABC沿着从B到D的方向平移后得到△EDF,若AB=16cm,AE=12cm,CE=4cm.
(1)指出△ABC平移的距离是多少?
(2)求线段BD、DE、EF的长.
13.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
14.如图,在边长为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点C移到了点C′的位置.
(1)画出平移后的△A′B′C′(点A′与点A对应,点B′与点B对应)
(2)指出平移的方向和平移的距离.
15.顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△A2B2C2;
(3)在(1)中△ABC向上平移过程中,边AC所扫过区域的面积是 .
16.如图:将四边形ABCD进行平移后,使点A的对应点为点A′,请你画出平移后所得的四边形A′B′C′D′(画图工具不限).
17.如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 .
10.2.2平移的特征
参考答案与试题解析
一.选择题(共8小题)
1.如图,△ABC经过平移到△DEF的位置,则下列四个“说法”中正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;③AC∥DF,AC=DF;④BC∥EF,BC=EF
A.1个 B.2个 C.3个 D.4个
【解答】解:①根据平移的性质可知AB∥DE,AB=DE正确;
②根据平移的性质可AD∥BE∥CF,AD=BE=CF正确;
③根据平移的性质可知AC∥DF,AC=DF正确;
④根据平移的性质可知BC∥EF,BC=EF正确.
故正确有个数有四个.
故选:D.
2.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
【解答】解:在四边形EFGH,EH是AD的对应边,∠F是∠B的对应角,
∵AD=5,∠B=70°,故EH=5,∠F=70°.
故选:B.
3.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
【解答】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
故选:A.
4.如图所示,是两个重叠的直角三角形,将其中的△ABC沿着BC方向平移BE的长得到△DEF,已知AB=8,BE=5,DH=3,则CF的长是( )
A.4 B.5 C.3 D.无法确定
【解答】解:根据平移的性质,
易得CF=BE=5,
故选:B.
5.如图,将△ABE向右平移2cm得到△DCF.如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16 cm B.18 cm C.20 cm D.21 cm
【解答】解:∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴四边形ABFD的周长=AB+BE+DF+AD+EF,
=AB+BE+AE+AD+EF,
=△ABE的周长+AD+EF,
∵平移距离为2cm,
∴AD=EF=2cm,
∵△ABE的周长是16cm,
∴四边形ABFD的周长=16+2+2=20cm.
故选:C.
6.如图,矩形ABCD经过平移后成为矩形EFGH,矩形长AD和宽AB分别为6和4,图中DE=5,那么矩形ABCD平移的距离为( )
A.11 B.10 C.6 D.4
【解答】解:由图可知,对应点A、E间的距离为平移距离,
∵AD=6,DE=5,
∴AE=AD+DE=6+5=11.
故选:A.
7.如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是( )
A.S1>S2 B.S1<S2 C.S1=S2 D.S1=2S2
【解答】解:
∵△ABC沿着BC方向平移得到△A′B′C′,
∴AA′∥BC′,
∵点P是直线AA′上任意一点,
∴△ABC,△PB′C′的高相等,
∴S1=S2,
故选:C.
8.如图,O是正六边形ABCDEF的中心,在这个正六边形中,可以由△OBC平移得到的三角形的个数是( )
A.1 B.2 C.3 D.4
【解答】解:△COD方向发生了变化,不属于平移得到;
△EOD形状和大小没有变化,属于平移得到;
△EOF方向发生了变化,不属于平移得到;
△FAO形状和大小没有变化,属于平移得到;
△ABO方向发生了变化,不属于平移得到.
∴可以由△OBC平移得到的是△EOD,△FAO.
故正确的有2个.
故选:B.
二.填空题(共3小题)
9.如图,将△ABC沿BC方向平移至△DEF处.若EC=2BE=2,则CF的长为 1 .
【解答】解:∵△ABC沿BC方向平移至△DEF处.
∴BE=CF,
∵EC=2BE=2,
∴BE=1,
∴CF=1.
故答案为1.
10.如图,长方形ABCD的长AD为6,宽AB为4,将这个长方形向上平移2个单位,再向右平移2个单位,得到长方形EFGH,则阴影部分的面积为 16 .
【解答】解:过点F作FN⊥BC于N,
由平移可得:AM=2,FN=2,
∴MD=AD﹣AM=6﹣2=4,MF=AB﹣FN=4﹣2=2,
∴阴影部分的面积=S矩形ABCD﹣S矩形MFQD=4×6﹣2×4=16,
故答案为:16.
11.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 15 .
【解答】解:设点A到BC的距离为h,则S△ABC=BC h=5,
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积=(AD+CE) h=(2BC+BC) h=3×BC h=3×5=15.
故答案为:15.
三.解答题(共6小题)
12.如图,将△ABC沿着从B到D的方向平移后得到△EDF,若AB=16cm,AE=12cm,CE=4cm.
(1)指出△ABC平移的距离是多少?
(2)求线段BD、DE、EF的长.
【解答】解:(1)∵AE=12cm,
∴平移的距离=AE=12cm;
(2)∵三角形ABC沿着从B到D的方向平移后得到三角形EDF,
∴BD=AE=12cm,DE=AB=16cm,EF=AC=AE﹣CE=16﹣4=8cm.
13.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE= 6 cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
【解答】解:(1)∵将△ABC沿直线AB向右平移得到△BDE,
∴△ABC≌△BDE,
∴BE=AC=6cm,
故答案为:6;
(2)由(1)知△ABC≌△BDE,
∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,
∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.
14.如图,在边长为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点C移到了点C′的位置.
(1)画出平移后的△A′B′C′(点A′与点A对应,点B′与点B对应)
(2)指出平移的方向和平移的距离.
【解答】解:(1)如图所示:△A′B′C′即为所求;
(2)如图连接CC′,平移方向是点C到点C′的方向,
平移距离为:CC′==.
15.顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△A2B2C2;
(3)在(1)中△ABC向上平移过程中,边AC所扫过区域的面积是 8 .
【解答】解:(1)如图,△A1B1C1即为所求;
(2)如图所示:△AB2C2即为所求;
(3)∵△ABC向上平移4个单位后得到的△A1B1C1,△ABC向上平移过程中,边AC所扫过区域是以4为边长,以2为高的平行四边形,
∴边AC所扫过区域的面积=4×2=8.
故答案为:8.
16.如图:将四边形ABCD进行平移后,使点A的对应点为点A′,请你画出平移后所得的四边形A′B′C′D′(画图工具不限).
【解答】解:
分别画四条平行线各(1分),共(4分),
连接四个顶点(2分).
17.如图,在方格纸中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点就是小正方形的格点,将△ABC向右平移3个单位长度再向下平移1个单位长度,得到△A′B′C′.
(1)在格中画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两段线段的关系是 平行且相等. ;
(3)用直尺作出平移后△A′B′C′高线A′D′;
(4)△ABC的面积是 3 .
【解答】解:(1)如图,△A′B′C′即为所求.
(2)如图,AA′∥CC′.
故答案为:平行且相等.
(3)如图,线段A′D′即为所求.
(4)△ABC的面积=2×4﹣×1×4﹣×1×2﹣×2×2=3,
故答案为:3.
