人教版版七年级数学上册1.3.1有理数的加法(第2课时)课件(共34张PPT)
文档属性
| 名称 | 人教版版七年级数学上册1.3.1有理数的加法(第2课时)课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 16:05:17 | ||
图片预览









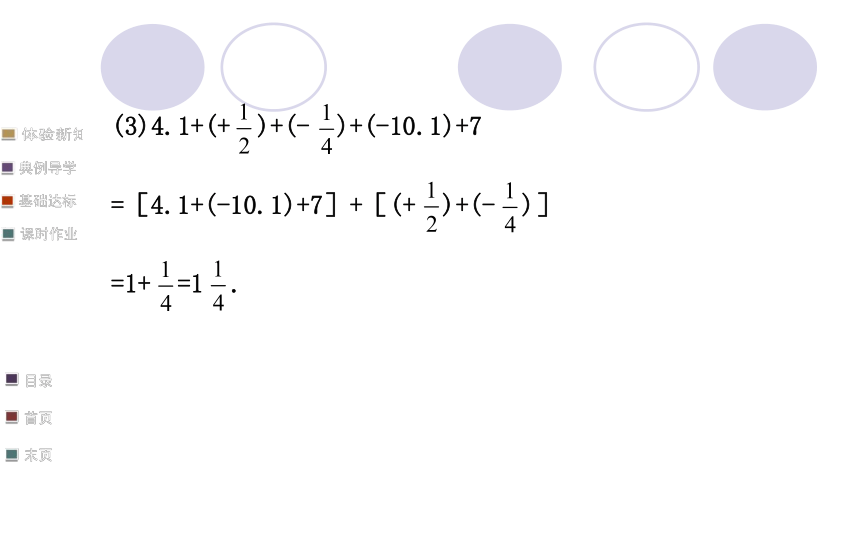
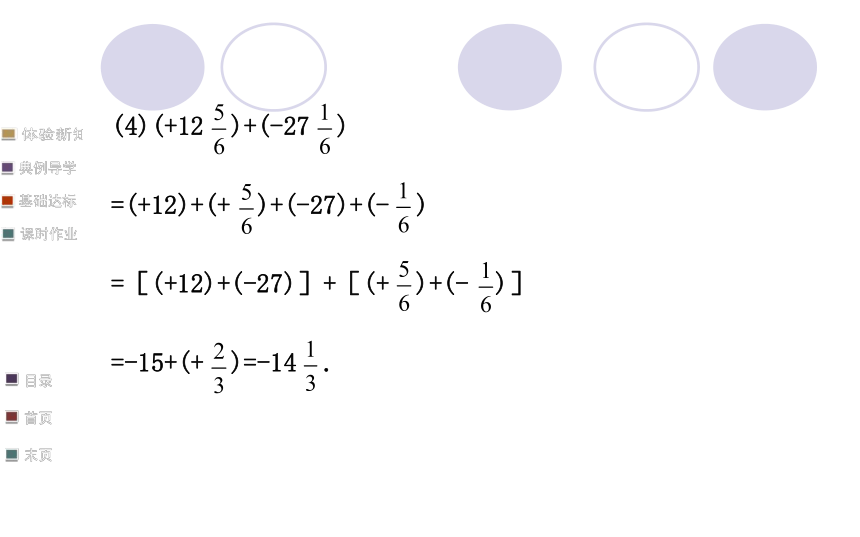

文档简介
(共34张PPT)
1.3.1 有理数的加法
第2课时
1.掌握有理数加法的运算律.(重点)
2.灵活运用运算律进行有理数的加法运算.(重点、难点)
3.会用有理数的加法解决实际问题.(难点)
填空:
(1)(-15)+4=____,4+(-15)=____,
于是(-15)+4__4+(-15).
(2)4+(-7)=___,(-7)+4=___,
于是4+(-7)__(-7)+4.
-11
-11
=
-3
-3
=
(3)[2+(-3)]+(-8)=___,
2+[(-3)+(-8)]=___,
于是[2+(-3)]+(-8)__2+[(-3)+(-8)].
(4)7+[(-7)+(-5)]=___,
[7+(-7)]+(-5)=___,
于是7+[(-7)+(-5)]__[7+(-7)]+(-5).
-9
-9
=
-5
-5
=
【归纳】1.有理数的加法中,两个数相加,交换加数的位置,和
_____.加法交换律: a+b=____.
2.有理数的加法中,三个数相加,先把前两个数相加,或者先把
后两个数相加,和_____.
加法结合律:(a+b)+c=________.
不变
b+a
不变
a+(b+c)
(打“√”或“×”)
(1)有理数的加法运算律中的a,b,c表示任意有理数.( )
(2)进行有理数的加法运算时,必须运用运算律.( )
(3)三个以上有理数相加,可以任意交换加数的位置,也可以
先把其中的几个数相加.( )
√
×
√
知识点 1 加法运算律的运用
【例1】计算:
(1)(-83)+(+26)+(-17)+(-26)+(+15).
(2) +(- )+(- )+(+ ).
(3)
(4)(+12 )+(-27 ).
【思路点拨】观察加数的特点→确定哪些数结合→运用运算律计算
【自主解答】(1)(-83)+(+26)+(-17)+(-26)+(+15)
=[(-83)+(-17)]+[(+26)+(-26)]+15
=(-100)+15=-85.
(2) +(- )+(- )+(+ )
=[ +(- )]+[(- )+(+ )]
=(- )+(+ )=- .
(3)4.1+(+ )+(- )+(-10.1)+7
=[4.1+(-10.1)+7]+[(+ )+(- )]
=1+ =1 .
(4)(+12 )+(-27 )
=(+12)+(+ )+(-27)+(- )
=[(+12)+(-27)]+[(+ )+(- )]
=-15+(+ )=-14 .
【总结提升】运用加法运算律时,有以下五个规律
1.互为相反数的两数,可先加——相反数结合法.
2.符号相同的数,可先加——同号结合法.
3.分母相同的分数,可先加——同形结合法.
4.几个数相加能得到整数的,可先加——凑整法.
5.带分数相加时,可先拆成整数和分数,再利用加法运算律相加——拆项结合法.
知识点 2 有理数加法的实际应用
【例2】有一批食品罐头,标准质量为每听454克.现抽取10听
样品进行检测,结果如表(单位:克):
这10听罐头的总质量是多少?请尝试用简便方法解决.
听号 1 2 3 4 5
质量 444 459 454 459 454
听号 6 7 8 9 10
质量 454 449 454 459 464
【解题探究】(1)标准质量为每听454克,如何表示所抽取的10
听样品与标准质量的差值?
提示:超过标准质量的克数记作正数,不足的克数记作负数.
即-10,+5,0,+5,0,0,-5,0,+5,+10.
(2)这10听罐头与标准质量差值的和为:
____________________________
_____________________________
_________,
因此,这10听罐头的总质量为:
______________________________.
(-10)+5+0+5+0+0+(-5)+0+5+10
=[(-10)+10]+[5+(-5)]+5+5
=10(克)
454×10+10=4 540+10=4 550(克)
【互动探究】如果这10听罐头与标准质量的差值和为0,那么
这10听罐头的总质量是多少克?
提示:这10听罐头的总质量是454×10+0=4 540(克).
【总结提升】有理数加法在实际中的应用
1.将实际问题转化为数学问题.
2.弄清问题的实质,列式计算,解答实际问题.
题组一:加法运算律的运用
1.7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应
用了( )
A.加法交换律 B.加法结合律
C.符号化简 D.加法交换律与结合律
【解析】选D.观察所给式子可知,在运算过程中应用了加法交
换律与结合律.
2.计算33+(-32)+7+(-8)的结果为( )
A.0 B.2 C.-1 D.5
【解析】选A. 33+(-32)+7+(-8)
=(33+7)+[(-32)+(-8)]
=40+(-40)=0.
3.计算: +(- )+ +(- )+(- )的正确结果是_________.
【解析】 +(- )+ +(- )+(- )
= +[(- )+(- )]+[ +(- )]
= +(-1)+0=- .
答案: -
4.绝对值大于5且小于10的所有整数的和为________.
【解析】绝对值大于5且小于10的所有整数有:
±6,±7,±8,±9,它们的和为0.
答案:0
5.计算下列各题:
(1) + +(- )+(- ).
(2)0.75+(-2 )+(-3 )+1.25.
【解析】(1) + +(- )+(- )
=[ +(- )]+[ +(- )]
=- + =- .
(2)0.75+(-2 )+(-3 )+1.25
=(0.75+1.25)+[(-2 )+(-3 )]
=2+(-6 )=-4 .
题组二:有理数加法的实际应用
1.七年级(1)班一学期班费收支情况如下(收入为正):+250
元,-55元,-120元,+7元.该班期末时班费增加了( )
A.82元 B.85元 C.90元 D.95元
【解析】选A.250+(-55)+(-120)+7
=250+7+[(-55)+(-120)]
=257+(-175)=82(元).
2.某天早晨气温是-3 ℃,到中午升高了5 ℃,傍晚又降低了
3 ℃,到午夜又降低了4 ℃,午夜的气温为( )
A.5 ℃ B.15 ℃ C.-5 ℃ D.-1 ℃
【解析】选C.由题意得,午夜的气温为:
(-3)+(+5)+(-3)+(-4)=-5(℃).
3.王老师2013年3月份打在工资卡上的工资是2 990元,同月用于买东西取出了1 500元,4月份打在工资卡上的工资是2 990元,同月用于买东西取出了1 900元,这两个月王老师的工资卡上一共多了(存入为正,取出为负)( )
A.2 370元 B.2 270元
C.2 360元 D.2 580元
【解析】选D.由题意得,
2 990+(-1 500)+2 990+(-1 900)=2 580(元).
4.五袋大米以每袋50千克为准,超过的记为正,不足的记为负,称重记录如下:+4.5,-4,+2.3,-3.5,+2.5,这五袋大米共超过标准_________千克,总质量是_________千克.
【解析】4.5+(-4)+2.3+(-3.5)+2.5
=[4.5+2.5+(-3.5)]+[(-4)+2.3]
=3.5+(-1.7)=1.8(千克),
50×5+1.8=251.8(千克).
答案:1.8 251.8
5.小明用32元钱买了8条毛巾,准备以一定的价格出售,如果每条毛巾以5元的价格为标准,超出部分记作正数,不足部分记作负数,记录如下:
0.5,-1,-1.5,1,-2,-1,2,0
当小明卖完毛巾后是盈利了还是亏损了 盈利或亏损多少元
【解析】超出部分与不足部分的总和为:
0.5+(-1)+(-1.5)+1+(-2)+(-1)+2+0=-2.
所以他实际总共卖了5×8+(-2)=38(元).
因为38>32,38-32=6,
所以小明卖完毛巾后盈利了6元.
6.有一批味精,标准质量为每袋100 g,现抽取10袋样品进行检测,其结果是:99,102,101,101,98,99,100,97,99,103(单位:g),用简便方法求这10袋味精的总质量是多少?
【解析】规定超过100 g的记为正,不足的记为负.则这10袋
味精与标准的差累计是:(-1)+(+2)+(+1)+(+1)+(-2)+(-1)+
0+(-3)+(-1)+(+3)=[(-1)+(+1)+(+2)+(-2)+(+1)+(-1)+
(-3)+(+3)]+[0+(-1)]=0+(-1)=-1(g).
所以100×10+(-1)=999(g).
答:这10袋味精的总质量是999 g.
【想一想错在哪?】计算:3 +(-2 )+5 +(-8 ).
提示:应用加法交换律时符号错,交换加数的位置时要连同符
号一起交换.
1.3.1 有理数的加法
第2课时
1.掌握有理数加法的运算律.(重点)
2.灵活运用运算律进行有理数的加法运算.(重点、难点)
3.会用有理数的加法解决实际问题.(难点)
填空:
(1)(-15)+4=____,4+(-15)=____,
于是(-15)+4__4+(-15).
(2)4+(-7)=___,(-7)+4=___,
于是4+(-7)__(-7)+4.
-11
-11
=
-3
-3
=
(3)[2+(-3)]+(-8)=___,
2+[(-3)+(-8)]=___,
于是[2+(-3)]+(-8)__2+[(-3)+(-8)].
(4)7+[(-7)+(-5)]=___,
[7+(-7)]+(-5)=___,
于是7+[(-7)+(-5)]__[7+(-7)]+(-5).
-9
-9
=
-5
-5
=
【归纳】1.有理数的加法中,两个数相加,交换加数的位置,和
_____.加法交换律: a+b=____.
2.有理数的加法中,三个数相加,先把前两个数相加,或者先把
后两个数相加,和_____.
加法结合律:(a+b)+c=________.
不变
b+a
不变
a+(b+c)
(打“√”或“×”)
(1)有理数的加法运算律中的a,b,c表示任意有理数.( )
(2)进行有理数的加法运算时,必须运用运算律.( )
(3)三个以上有理数相加,可以任意交换加数的位置,也可以
先把其中的几个数相加.( )
√
×
√
知识点 1 加法运算律的运用
【例1】计算:
(1)(-83)+(+26)+(-17)+(-26)+(+15).
(2) +(- )+(- )+(+ ).
(3)
(4)(+12 )+(-27 ).
【思路点拨】观察加数的特点→确定哪些数结合→运用运算律计算
【自主解答】(1)(-83)+(+26)+(-17)+(-26)+(+15)
=[(-83)+(-17)]+[(+26)+(-26)]+15
=(-100)+15=-85.
(2) +(- )+(- )+(+ )
=[ +(- )]+[(- )+(+ )]
=(- )+(+ )=- .
(3)4.1+(+ )+(- )+(-10.1)+7
=[4.1+(-10.1)+7]+[(+ )+(- )]
=1+ =1 .
(4)(+12 )+(-27 )
=(+12)+(+ )+(-27)+(- )
=[(+12)+(-27)]+[(+ )+(- )]
=-15+(+ )=-14 .
【总结提升】运用加法运算律时,有以下五个规律
1.互为相反数的两数,可先加——相反数结合法.
2.符号相同的数,可先加——同号结合法.
3.分母相同的分数,可先加——同形结合法.
4.几个数相加能得到整数的,可先加——凑整法.
5.带分数相加时,可先拆成整数和分数,再利用加法运算律相加——拆项结合法.
知识点 2 有理数加法的实际应用
【例2】有一批食品罐头,标准质量为每听454克.现抽取10听
样品进行检测,结果如表(单位:克):
这10听罐头的总质量是多少?请尝试用简便方法解决.
听号 1 2 3 4 5
质量 444 459 454 459 454
听号 6 7 8 9 10
质量 454 449 454 459 464
【解题探究】(1)标准质量为每听454克,如何表示所抽取的10
听样品与标准质量的差值?
提示:超过标准质量的克数记作正数,不足的克数记作负数.
即-10,+5,0,+5,0,0,-5,0,+5,+10.
(2)这10听罐头与标准质量差值的和为:
____________________________
_____________________________
_________,
因此,这10听罐头的总质量为:
______________________________.
(-10)+5+0+5+0+0+(-5)+0+5+10
=[(-10)+10]+[5+(-5)]+5+5
=10(克)
454×10+10=4 540+10=4 550(克)
【互动探究】如果这10听罐头与标准质量的差值和为0,那么
这10听罐头的总质量是多少克?
提示:这10听罐头的总质量是454×10+0=4 540(克).
【总结提升】有理数加法在实际中的应用
1.将实际问题转化为数学问题.
2.弄清问题的实质,列式计算,解答实际问题.
题组一:加法运算律的运用
1.7+(-3)+(-4)+18+(-11)=(7+18)+[(-3)+(-4)+(-11)]是应
用了( )
A.加法交换律 B.加法结合律
C.符号化简 D.加法交换律与结合律
【解析】选D.观察所给式子可知,在运算过程中应用了加法交
换律与结合律.
2.计算33+(-32)+7+(-8)的结果为( )
A.0 B.2 C.-1 D.5
【解析】选A. 33+(-32)+7+(-8)
=(33+7)+[(-32)+(-8)]
=40+(-40)=0.
3.计算: +(- )+ +(- )+(- )的正确结果是_________.
【解析】 +(- )+ +(- )+(- )
= +[(- )+(- )]+[ +(- )]
= +(-1)+0=- .
答案: -
4.绝对值大于5且小于10的所有整数的和为________.
【解析】绝对值大于5且小于10的所有整数有:
±6,±7,±8,±9,它们的和为0.
答案:0
5.计算下列各题:
(1) + +(- )+(- ).
(2)0.75+(-2 )+(-3 )+1.25.
【解析】(1) + +(- )+(- )
=[ +(- )]+[ +(- )]
=- + =- .
(2)0.75+(-2 )+(-3 )+1.25
=(0.75+1.25)+[(-2 )+(-3 )]
=2+(-6 )=-4 .
题组二:有理数加法的实际应用
1.七年级(1)班一学期班费收支情况如下(收入为正):+250
元,-55元,-120元,+7元.该班期末时班费增加了( )
A.82元 B.85元 C.90元 D.95元
【解析】选A.250+(-55)+(-120)+7
=250+7+[(-55)+(-120)]
=257+(-175)=82(元).
2.某天早晨气温是-3 ℃,到中午升高了5 ℃,傍晚又降低了
3 ℃,到午夜又降低了4 ℃,午夜的气温为( )
A.5 ℃ B.15 ℃ C.-5 ℃ D.-1 ℃
【解析】选C.由题意得,午夜的气温为:
(-3)+(+5)+(-3)+(-4)=-5(℃).
3.王老师2013年3月份打在工资卡上的工资是2 990元,同月用于买东西取出了1 500元,4月份打在工资卡上的工资是2 990元,同月用于买东西取出了1 900元,这两个月王老师的工资卡上一共多了(存入为正,取出为负)( )
A.2 370元 B.2 270元
C.2 360元 D.2 580元
【解析】选D.由题意得,
2 990+(-1 500)+2 990+(-1 900)=2 580(元).
4.五袋大米以每袋50千克为准,超过的记为正,不足的记为负,称重记录如下:+4.5,-4,+2.3,-3.5,+2.5,这五袋大米共超过标准_________千克,总质量是_________千克.
【解析】4.5+(-4)+2.3+(-3.5)+2.5
=[4.5+2.5+(-3.5)]+[(-4)+2.3]
=3.5+(-1.7)=1.8(千克),
50×5+1.8=251.8(千克).
答案:1.8 251.8
5.小明用32元钱买了8条毛巾,准备以一定的价格出售,如果每条毛巾以5元的价格为标准,超出部分记作正数,不足部分记作负数,记录如下:
0.5,-1,-1.5,1,-2,-1,2,0
当小明卖完毛巾后是盈利了还是亏损了 盈利或亏损多少元
【解析】超出部分与不足部分的总和为:
0.5+(-1)+(-1.5)+1+(-2)+(-1)+2+0=-2.
所以他实际总共卖了5×8+(-2)=38(元).
因为38>32,38-32=6,
所以小明卖完毛巾后盈利了6元.
6.有一批味精,标准质量为每袋100 g,现抽取10袋样品进行检测,其结果是:99,102,101,101,98,99,100,97,99,103(单位:g),用简便方法求这10袋味精的总质量是多少?
【解析】规定超过100 g的记为正,不足的记为负.则这10袋
味精与标准的差累计是:(-1)+(+2)+(+1)+(+1)+(-2)+(-1)+
0+(-3)+(-1)+(+3)=[(-1)+(+1)+(+2)+(-2)+(+1)+(-1)+
(-3)+(+3)]+[0+(-1)]=0+(-1)=-1(g).
所以100×10+(-1)=999(g).
答:这10袋味精的总质量是999 g.
【想一想错在哪?】计算:3 +(-2 )+5 +(-8 ).
提示:应用加法交换律时符号错,交换加数的位置时要连同符
号一起交换.
