二元一次不等式和线性规划
图片预览





文档简介
课件27张PPT。二元一次不等式(组)与平面区域二元一次不等式(组) 一家银行的信贷部计划年初投入25 000 000元用于企业投资和个人贷款,希望这笔资金至少可带来30 000元的收益,其中从企业贷款中获益12﹪,从个人贷款中获益10﹪,那么信贷部应该如何分配资金呢?二元一次不等式:含有两个未知数,并且未知数的最高次数是1的不等式
二元一次不等式组:由几个二元一次不等式组成的不等式组
二元一次不等式(组)的解集:满足二元一次不等式(组)的有序实数对(x,y)构成的集合
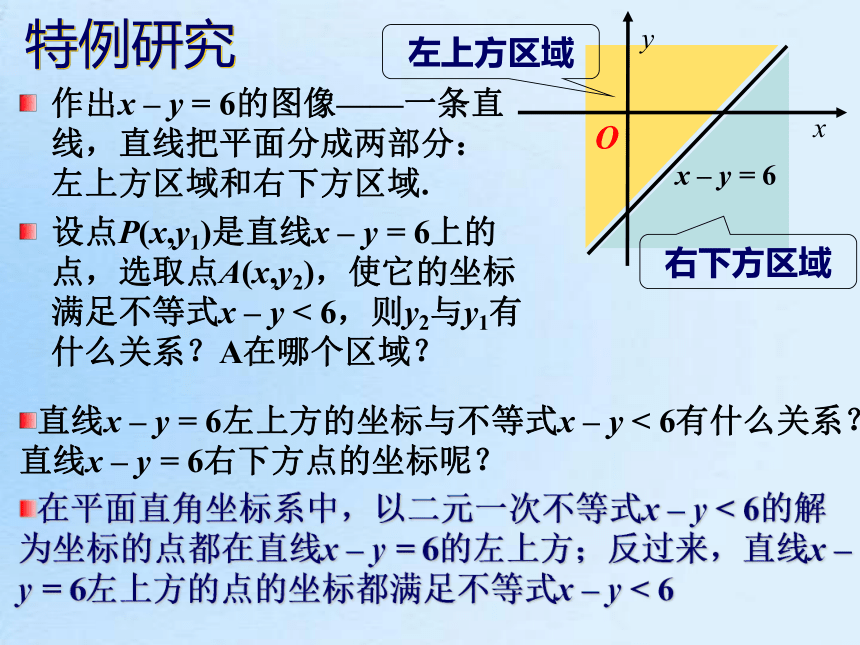
二元一次不等式(组)的解集可以看成是直角坐标系内的点构成的集合类比推广回忆:一元一次不等式(组)的解集所表示的图形数轴上的区间,一维思考:二元一次不等式(组)的解集表示什么图形? 猜想:平面区域,二维具体问题:二元一次不等式x – y < 6的解集所表示的图形特例研究作出x – y = 6的图像——一条直线,直线把平面分成两部分: 左上方区域和右下方区域.
设点P(x,y1)是直线x – y = 6上的点,选取点A(x,y2),使它的坐标满足不等式x – y < 6,则y2与y1有什么关系?A在哪个区域?
左上方区域右下方区域直线x – y = 6左上方的坐标与不等式x – y < 6有什么关系?直线x – y = 6右下方点的坐标呢?
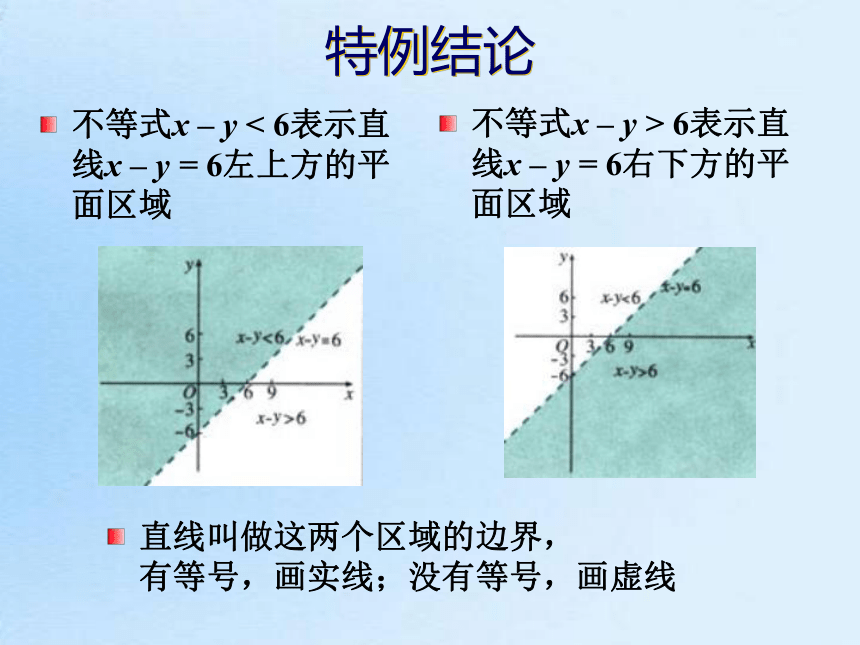
在平面直角坐标系中,以二元一次不等式x – y < 6的解为坐标的点都在直线x – y = 6的左上方;反过来,直线x – y = 6左上方的点的坐标都满足不等式x – y < 6 特例结论不等式x – y < 6表示直线x – y = 6左上方的平面区域不等式x – y > 6表示直线x – y = 6右下方的平面区域直线叫做这两个区域的边界, 有等号,画实线;没有等号,画虚线二元一次不等式表示的平面区域结论1:二元一次不等式表示相应直线的某一侧区域
二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域(虚线表示区域不包括边界直线)
结论2:直线定界,特殊点定域
直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域,C≠0时,常把原点作为特殊点
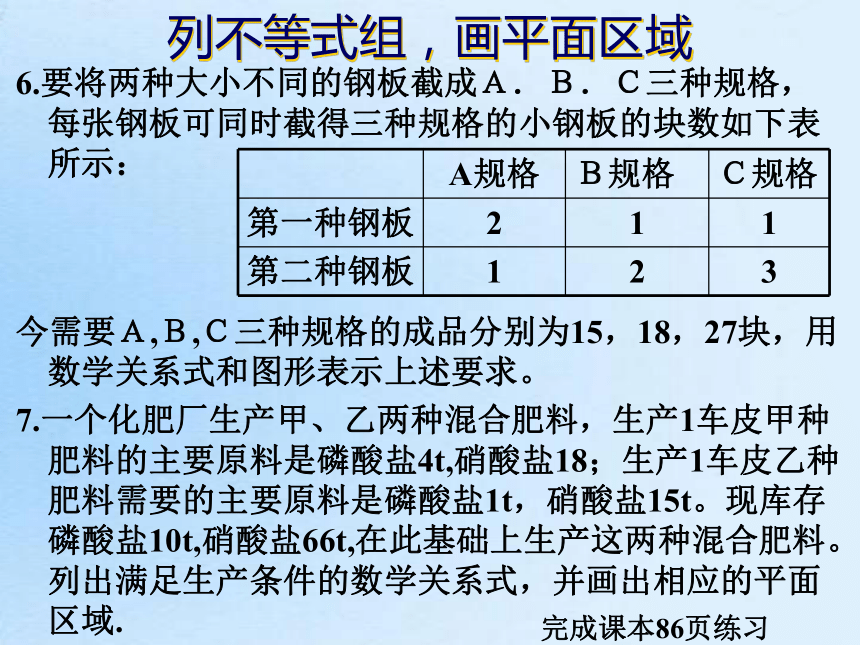
注意所求区域是否包括边界直线(实线与虚线)画平面区域列不等式组,画平面区域6.要将两种大小不同的钢板截成A.B.C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
今需要A,B,C三种规格的成品分别为15,18,27块,用数学关系式和图形表示上述要求。
7.一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域.完成课本86页练习逆向:写不等式(组)8.用不等式组表示下列平面区域练习完成《创新》随堂反馈练习简单的线性规划问题引例 一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。若生产1车皮甲种肥料获利1万元;生产1车皮乙种肥料获利0.5万元。那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?
如何求z的最大值?温故而知新回顾与圆有关的最值问题原理类比:圆→平面区域M(2,2)相关概念及变式M(2,2)线性约束条件目标函数可行域最优解在线性约束条件下求目标函数的最值——线性规划比较目标函数的斜率与区域边界直线的斜率,确定最优解线性规划相关概念由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。
欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y的一次目标函数称为线性目标函数。
求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。
满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。
使目标函数取得最大值或最小值的可行解称为最优解。线性规划基础练习比较目标函数的斜率与区域边界直线的斜率,确定最优解解决线性规划问题的基本步骤画:画出线性约束条件所表示的可行域;
移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
求:通过解方程组求出最优解;
答:作出答案。1、线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得。
2、比较目标函数的斜率与区域边界直线的斜率,确定最优解。线性规划应用题类型一:在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务.
课本例题:某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h;该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算。若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
线性规划应用题类型二:给定一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务.
课本例题:营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?应用题练习1.《创新》某企业生产A,B两种产品,每生产一吨产品所需要的劳动力和煤、电如下表:
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200度,试问该企业生产A,B两种产品各多少吨时,才能获得最大利润?最大利润为多少?2.某公司仓库A存有货物12吨,仓库B存有货物8吨,现按7吨、8吨和5吨把货物分别调运给甲、乙、丙三个商店,从仓库A运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元;从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元. 问应如何安排调运方案,才能使得从两个仓库运货物到三个商店的总运费最少?
3.某运输公司有7辆载重6t的A型卡车,4辆载重10t的B型卡车,有9名驾驶员。在建造某段高速公路中,公司承包了每天至少运输沥青360t的任务。已知每辆卡车每天往返次数为A型8次,B型6次,每天运输成本为A型160元,B型252元。每天应派出A型、B型车各多少辆,能使公司总成本最低?线性规划问题的几个难点研究目标函数最优解(06重庆)变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2,若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围是______.
在如图所示的可行域内(阴影部分且包括边界),目标函数z=x+ay取得最小值的最优解有无数个,则a的一个可能值为( ) A.-3 B.3 C.-1 D.1整点找整点,先求出边界点的坐标,再逐一定x(或y)的值,按竖线(或横线)找可行域面积综合运用最优整数解问题2.课本例题:要将两种大小不同的钢板截成A,B,C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张,使所用钢板张数最少?先按常规方法求出z最值,再对z取整,得到x与y的等量关系,代入约束条件,解得最优整点坐标.
二元一次不等式组:由几个二元一次不等式组成的不等式组
二元一次不等式(组)的解集:满足二元一次不等式(组)的有序实数对(x,y)构成的集合
二元一次不等式(组)的解集可以看成是直角坐标系内的点构成的集合类比推广回忆:一元一次不等式(组)的解集所表示的图形数轴上的区间,一维思考:二元一次不等式(组)的解集表示什么图形? 猜想:平面区域,二维具体问题:二元一次不等式x – y < 6的解集所表示的图形特例研究作出x – y = 6的图像——一条直线,直线把平面分成两部分: 左上方区域和右下方区域.
设点P(x,y1)是直线x – y = 6上的点,选取点A(x,y2),使它的坐标满足不等式x – y < 6,则y2与y1有什么关系?A在哪个区域?
左上方区域右下方区域直线x – y = 6左上方的坐标与不等式x – y < 6有什么关系?直线x – y = 6右下方点的坐标呢?
在平面直角坐标系中,以二元一次不等式x – y < 6的解为坐标的点都在直线x – y = 6的左上方;反过来,直线x – y = 6左上方的点的坐标都满足不等式x – y < 6 特例结论不等式x – y < 6表示直线x – y = 6左上方的平面区域不等式x – y > 6表示直线x – y = 6右下方的平面区域直线叫做这两个区域的边界, 有等号,画实线;没有等号,画虚线二元一次不等式表示的平面区域结论1:二元一次不等式表示相应直线的某一侧区域
二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域(虚线表示区域不包括边界直线)
结论2:直线定界,特殊点定域
直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域,C≠0时,常把原点作为特殊点
注意所求区域是否包括边界直线(实线与虚线)画平面区域列不等式组,画平面区域6.要将两种大小不同的钢板截成A.B.C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
今需要A,B,C三种规格的成品分别为15,18,27块,用数学关系式和图形表示上述要求。
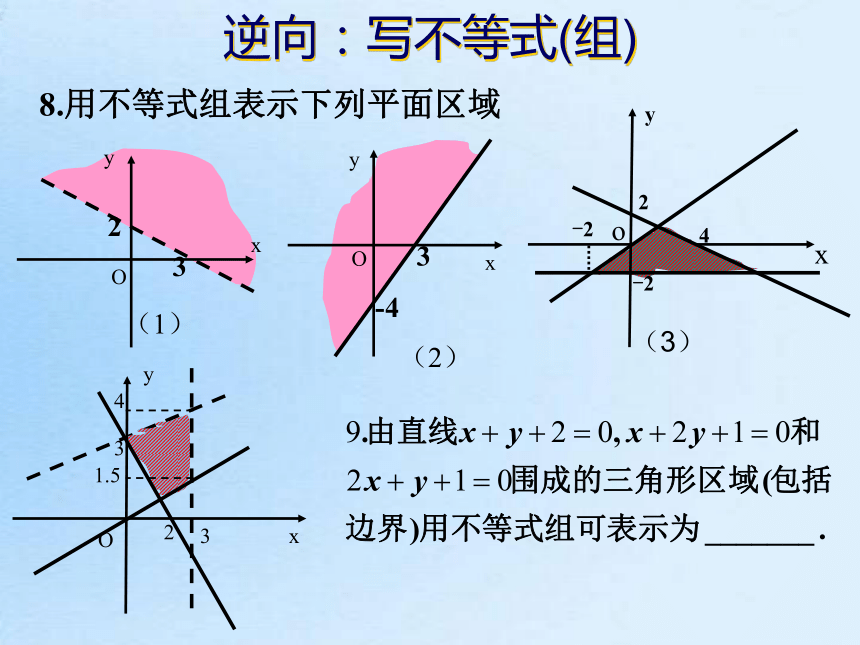
7.一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。列出满足生产条件的数学关系式,并画出相应的平面区域.完成课本86页练习逆向:写不等式(组)8.用不等式组表示下列平面区域练习完成《创新》随堂反馈练习简单的线性规划问题引例 一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18;生产1车皮乙种肥料需要的主要原料是磷酸盐1t,硝酸盐15t。现库存磷酸盐10t,硝酸盐66t,在此基础上生产这两种混合肥料。若生产1车皮甲种肥料获利1万元;生产1车皮乙种肥料获利0.5万元。那么分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?
如何求z的最大值?温故而知新回顾与圆有关的最值问题原理类比:圆→平面区域M(2,2)相关概念及变式M(2,2)线性约束条件目标函数可行域最优解在线性约束条件下求目标函数的最值——线性规划比较目标函数的斜率与区域边界直线的斜率,确定最优解线性规划相关概念由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。
欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y的一次目标函数称为线性目标函数。
求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。
满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。
使目标函数取得最大值或最小值的可行解称为最优解。线性规划基础练习比较目标函数的斜率与区域边界直线的斜率,确定最优解解决线性规划问题的基本步骤画:画出线性约束条件所表示的可行域;
移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
求:通过解方程组求出最优解;
答:作出答案。1、线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得。
2、比较目标函数的斜率与区域边界直线的斜率,确定最优解。线性规划应用题类型一:在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务.
课本例题:某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h;该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算。若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
线性规划应用题类型二:给定一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务.
课本例题:营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?应用题练习1.《创新》某企业生产A,B两种产品,每生产一吨产品所需要的劳动力和煤、电如下表:
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200度,试问该企业生产A,B两种产品各多少吨时,才能获得最大利润?最大利润为多少?2.某公司仓库A存有货物12吨,仓库B存有货物8吨,现按7吨、8吨和5吨把货物分别调运给甲、乙、丙三个商店,从仓库A运货物到商店甲、乙、丙,每吨货物的运费分别为8元、6元、9元;从仓库B运货物到商店甲、乙、丙,每吨货物的运费分别为3元、4元、5元. 问应如何安排调运方案,才能使得从两个仓库运货物到三个商店的总运费最少?
3.某运输公司有7辆载重6t的A型卡车,4辆载重10t的B型卡车,有9名驾驶员。在建造某段高速公路中,公司承包了每天至少运输沥青360t的任务。已知每辆卡车每天往返次数为A型8次,B型6次,每天运输成本为A型160元,B型252元。每天应派出A型、B型车各多少辆,能使公司总成本最低?线性规划问题的几个难点研究目标函数最优解(06重庆)变量x,y满足约束条件1≤x+y≤4,-2≤x-y≤2,若目标函数z=ax+y(其中a>0)仅在点(3,1)处取得最大值,则a的取值范围是______.
在如图所示的可行域内(阴影部分且包括边界),目标函数z=x+ay取得最小值的最优解有无数个,则a的一个可能值为( ) A.-3 B.3 C.-1 D.1整点找整点,先求出边界点的坐标,再逐一定x(或y)的值,按竖线(或横线)找可行域面积综合运用最优整数解问题2.课本例题:要将两种大小不同的钢板截成A,B,C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张,使所用钢板张数最少?先按常规方法求出z最值,再对z取整,得到x与y的等量关系,代入约束条件,解得最优整点坐标.
