初中数学人教版九年级下册27.2.3 相似三角形的应用举例 教案(表格式)
文档属性
| 名称 | 初中数学人教版九年级下册27.2.3 相似三角形的应用举例 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览

文档简介
课题 27.2.3 相似三角形的应用(第一课时)
上课教师 上课时间 第 周 第 节
教学 目标 理解并掌握测量不可及物体的高度、宽度时通常是利用相似三角形的性质 即对应线段的比相等来解决. 理解并掌握利用相似三角形解决实际问题的核心是构造相似三角形,在构造的 三角形中被测物体的高或宽是其中- -边. 准确理解题意,把实际问题转化为数学问题,运用数学建模思想和数形结合思想 灵活地解决问题.
教学 重点 运用两个三角形相似解决实际问题
教学 难点 在实际问题中建立数学模型
教 学 过 程
环节 教师活动 学生活动 设计意图
课前预习 1、布置学生的课前预习任务; 2、进行预习方法指导; 3、对学生预习任务进行检查与评定。 1、认真阅读教材39---40页例4、例5,用铅笔勾画重点、疑点; 2、完成《练习册》例1、例2。 培养学生课前预习习惯,提升学生自主学习能力。
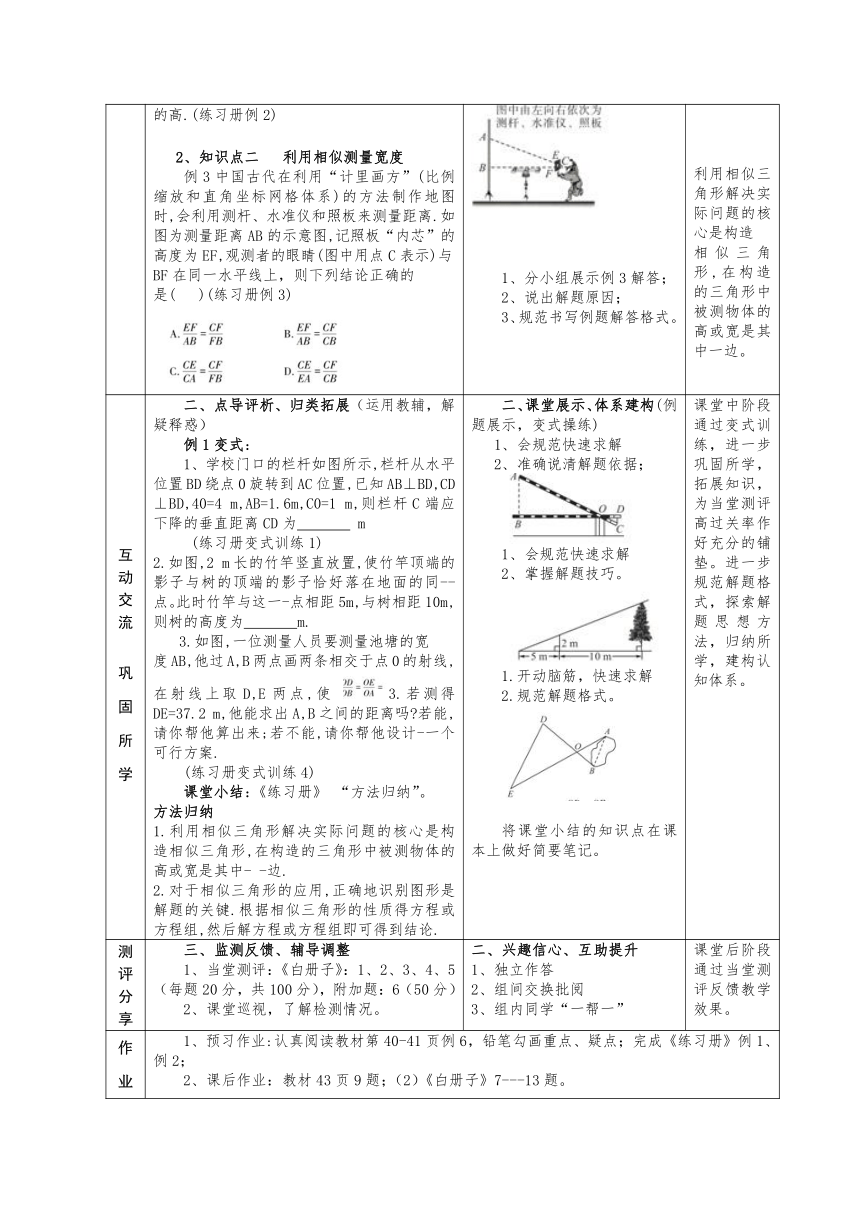
自主学习 理解新知 一、师生互动、引问激思(运用教材,梳理知识) 1、知识点一 利用相似测量高度 例1如图,学校平房的窗外有一路灯AB, 路灯的光能通过窗户CD照到平房内EF处,经 过测量得到窗户距地面的高0D=1.5 m,窗户高 度DC=0.8 m,OE=1 m,OF=3 m,求路灯AB的高. (练习册例1) 例2如图, 小华和小康想用标杆来测量河 对岸的树AB的高。在确保无安全隐患的情况下。小康在F处竖立了一根标杆EF,小华站立在C处看到标杆顶端E和树的顶端B在-条直线上.此时测得小华的眼睛到地面的距离DC=1.6 m然后,小华在C处蹲下,小康平移标杆到H处.时,小华恰好看到标杆頂端C和树的頂端B在一条直线上,此时测得小华的眼睛 到地面的距离MC=0.8 m.已知EF =CH=24m.CF =2 m.FH=1.6m,点C,F,H,A在-条直线上,点M在CD上.CD⊥AC,EF⊥AC. GH⊥AC.AB⊥AC,根 据以上测量过程及测量数据,请你求出树AB 的高.(练习册例2) 2、知识点二 利用相似测量宽度 例3中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.如图为测量距离AB的示意图,记照板“内芯”的高度为EF,观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论正确的 是( )(练习册例3) 一、进入情境、领会所学(理解教材,领悟新知) 1、分小组分享例1、例2解答; 2、在课本上用红色笔勾画标记解决问题的过程,体会利用三角形的相似,如何解决一些不能直接测量的物体的长度的问题? 1、分小组展示例3解答; 2、说出解题原因; 3、规范书写例题解答格式。 课堂前阶段通过师生互动,学生温故知新,领会利用三角形的相似,如何解决一些不能直接测量的物体的长度的问题。 类比例1,修订不规范解答,为后续变式练习作铺垫。 利用相似三角形解决实际问题的核心是构造 相似三角形,在构造的三角形中被测物体的高或宽是其中一边。
互动交流 巩固所学 二、点导评析、归类拓展(运用教辅,解疑释惑) 例1变式: 1、学校门口的栏杆如图所示,栏杆从水平位置BD绕点0旋转到AC位置,已知AB⊥BD,CD⊥BD,40=4 m,AB=1.6m,C0=1 m,则栏杆C端应下降的垂直距离CD为 m (练习册变式训练1) 2.如图,2 m长的竹竿竖直放置,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同--点。此时竹竿与这一-点相距5m,与树相距10m,则树的高度为 m. 3.如图,一位测量人员要测量池塘的宽 度AB,他过A,B两点画两条相交于点0的射线,在射线上取D,E两点,使 3.若测得DE=37.2 m,他能求出A,B之间的距离吗 若能,请你帮他算出来;若不能,请你帮他设计-一个可行方案. (练习册变式训练4) 课堂小结:《练习册》 “方法归纳”。 方法归纳 1.利用相似三角形解决实际问题的核心是构造相似三角形,在构造的三角形中被测物体的高或宽是其中- -边. 2.对于相似三角形的应用,正确地识别图形是解题的关键.根据相似三角形的性质得方程或方程组,然后解方程或方程组即可得到结论. 二、课堂展示、体系建构(例题展示,变式操练) 1、会规范快速求解 2、准确说清解题依据; 会规范快速求解 2、掌握解题技巧。 1.开动脑筋,快速求解 2.规范解题格式。 将课堂小结的知识点在课本上做好简要笔记。 课堂中阶段通过变式训练,进一步巩固所学,拓展知识,为当堂测评高过关率作好充分的铺垫。进一步规范解题格式,探索解题思想方法,归纳所学,建构认知体系。
测评分享 三、监测反馈、辅导调整 1、当堂测评:《白册子》:1、2、3、4、5(每题20分,共100分),附加题:6(50分) 课堂巡视,了解检测情况。 兴趣信心、互助提升 1、独立作答 2、组间交换批阅 3、组内同学“一帮一” 课堂后阶段通过当堂测评反馈教学效果。
作业 1、预习作业:认真阅读教材第40-41页例6,铅笔勾画重点、疑点;完成《练习册》例1、例2; 2、课后作业:教材43页9题;(2)《白册子》7---13题。
反思
课题 27.2.3 相似三角形的应用(第二课时)
上课教师 上课时间 第 周 第 节
教学 目标 1.进一步巩固相似三角形的相关知识. 2.能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题.测量河宽问题、盲区问题)等的一些实际问题. 3.通过把实际问题转化成与相似三角形有关的数学模型,进-一步了解数学建模思想,培养学生分析问题、解决问题的能力.
教学 重点 运用两个三角形相似解决实际问题
教学 难点 在实际问题中建立数学模型
教 学 过 程
环节 教师活动 学生活动 设计意图
课前预习 1.布置学生的课前预习任务; 2.进行预习方法指导; 3.对学生预习任务进行检查与评定。 1、认真阅读教材40---41页例6,用铅笔勾画重点、疑点; 2、完成《练习册》例1、例2。 培养学生课前预习习惯,提升学生自主学习能力。
自主学习 理解新知 师生互动、引问激思 1、知识点一:利用影长、平面镜测量物体高度 例1如图,小颍为测量学校旗杆AB的高度,她在E处放置-块镜子.然后退到C处站立.刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D 离地面的高度CD=1.5 m,她离镜子的水平距离CE =0.5 m,镜子E离旗杆的底部A处的距离AE=2 m,且A,C,E三点在同-水平直线上,则旗杆AB的高度为( ) A.4.0 m B.4.8 m C.5.5 m D.6 m(练习册例1) 例2 如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC =2 m,BD =2.1m.如果小明眼睛距地面高度BF=DG=1. 6 m,试确定楼的高度OE.(练习册例2) 2、知识点二:相似三角形在实际问题中的应用 例3如图. 在相对的两栋楼中间有一堵墙,甲.乙两人分别在这两栋楼内观察这堵墙.视线如图①所示根据实际情况画出平而图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以 看到点G处,乙从点E可以看到点D处,点B是 DF的中点,墙AB高5.5 m,DF=100 m, BG=10.5 m.求甲,乙两人的观测点到地面的距离之差(结果精确到0.1 m)(练习册例3) 一、进入情境、领会所学(理解教材,领悟新知) 1、分小组分享例1、例2解答; 2、在课本上用红色笔勾画标记解决问题的过程,体会实际问题中建立数学模型思想。 1、分小组展示例3解答; 2、说出解题原因; 3、规范书写例题解答格式。 课堂前阶段通过师生互动,学生温故知新,领会利用三角形的相似,如何解决一些不能直接测量的物体的长度的问题。 类比例1,修订不规范解答,为后续变式练习作铺垫。 利用相似三角形解决实际问题的核心是构造 相似三角形,在构造的三角形中被测物体的高或宽是其中一边.
互动交流 巩固所学 二、点导评析、归类拓展(运用教辅,解疑释惑) 例1变式: 1.如图是小明设计用手电简来测量某古城墙高度的示意图.在地面上点P处放一-水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD, CD⊥BD,且测得AB=1.2 m,BP=1.8m,PD= 18 m,那么古城墙的高度是( ) A.6m B.8m C.12m D.24m(练习册变式训练1) 2.某小组想利用镜子与皮尺测量大树AB的高 度,因大树底部有障碍物,无法直接测量到大树底部的距离.小颍借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时.刚好看到大树的顶端,沿大树方向向前走2.8 m,到达点D处.将镜子放在点N处时.刚好看到大树的顶端(点F.M,D,N,B在同一条直线上).若测得FM =1.5 m,DN=1.1 m,测量者眼睛到地面的距离为1.6 m,求大树AB的高度.(练习册变式训练2) 3.如图,为了估计河的寬度,在河的对岸选定 一个目标点P,在近岸取点Q和S.使点P,Q.S在一条直线上,且直线PS与河岸垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60 m,ST=120m,QR=80m,则河的宽度PQ为( )(练习册变式训练3) A.40m B.60m C.120m D. 180 m . 课堂小结:《练习册》 “方法归纳”。 方法归纳 1.对于相似三角形的应用,解题的关键是从实际问题中找出相似三角形.可借助标杆或直尺,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度. 2.可利用影长测量物体的高度,利用相似测量河的宽度(测量距离).解题的关键是根据实际问题抽象出几何图形,再利用相似三角形知识解题,要注意数形结合思想的应用. 二、课堂展示、体系建构(例题展示,变式操练) 会规范快速求解 2、准确说清解题依据; 会规范快速求解 2、掌握解题技巧。 1.开动脑筋,快速求解 2.规范解题格式。 将课堂小结的知识点在课本上做好简要笔记。 课堂中阶段通过变式训练,进一步巩固所学,拓展知识,为当堂测评高过关率作好充分的铺垫。进一步规范解题格式,探索解题思想方法,归纳所学,建构认知体系。
测评分享 三、监测反馈、辅导调整 1、当堂测评:《白册子》:1、2、3、4、5(每题20分,共100分),附加题:6(50分) 2.课堂巡视,了解检测情况。 三、兴趣信心、互助提升(满意高分,组间争雄) 独立作答 组间交换批阅 3、组内同学“一帮一” 及时解决存在问题
作业 预习作业:认真阅读教材第47-48页内容,铅笔勾画重点、疑点;完成《练习册》例1、例2; 课后作业:(1)教材43页10题;(2)《白册子》7---13题。
反思
上课教师 上课时间 第 周 第 节
教学 目标 理解并掌握测量不可及物体的高度、宽度时通常是利用相似三角形的性质 即对应线段的比相等来解决. 理解并掌握利用相似三角形解决实际问题的核心是构造相似三角形,在构造的 三角形中被测物体的高或宽是其中- -边. 准确理解题意,把实际问题转化为数学问题,运用数学建模思想和数形结合思想 灵活地解决问题.
教学 重点 运用两个三角形相似解决实际问题
教学 难点 在实际问题中建立数学模型
教 学 过 程
环节 教师活动 学生活动 设计意图
课前预习 1、布置学生的课前预习任务; 2、进行预习方法指导; 3、对学生预习任务进行检查与评定。 1、认真阅读教材39---40页例4、例5,用铅笔勾画重点、疑点; 2、完成《练习册》例1、例2。 培养学生课前预习习惯,提升学生自主学习能力。
自主学习 理解新知 一、师生互动、引问激思(运用教材,梳理知识) 1、知识点一 利用相似测量高度 例1如图,学校平房的窗外有一路灯AB, 路灯的光能通过窗户CD照到平房内EF处,经 过测量得到窗户距地面的高0D=1.5 m,窗户高 度DC=0.8 m,OE=1 m,OF=3 m,求路灯AB的高. (练习册例1) 例2如图, 小华和小康想用标杆来测量河 对岸的树AB的高。在确保无安全隐患的情况下。小康在F处竖立了一根标杆EF,小华站立在C处看到标杆顶端E和树的顶端B在-条直线上.此时测得小华的眼睛到地面的距离DC=1.6 m然后,小华在C处蹲下,小康平移标杆到H处.时,小华恰好看到标杆頂端C和树的頂端B在一条直线上,此时测得小华的眼睛 到地面的距离MC=0.8 m.已知EF =CH=24m.CF =2 m.FH=1.6m,点C,F,H,A在-条直线上,点M在CD上.CD⊥AC,EF⊥AC. GH⊥AC.AB⊥AC,根 据以上测量过程及测量数据,请你求出树AB 的高.(练习册例2) 2、知识点二 利用相似测量宽度 例3中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.如图为测量距离AB的示意图,记照板“内芯”的高度为EF,观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论正确的 是( )(练习册例3) 一、进入情境、领会所学(理解教材,领悟新知) 1、分小组分享例1、例2解答; 2、在课本上用红色笔勾画标记解决问题的过程,体会利用三角形的相似,如何解决一些不能直接测量的物体的长度的问题? 1、分小组展示例3解答; 2、说出解题原因; 3、规范书写例题解答格式。 课堂前阶段通过师生互动,学生温故知新,领会利用三角形的相似,如何解决一些不能直接测量的物体的长度的问题。 类比例1,修订不规范解答,为后续变式练习作铺垫。 利用相似三角形解决实际问题的核心是构造 相似三角形,在构造的三角形中被测物体的高或宽是其中一边。
互动交流 巩固所学 二、点导评析、归类拓展(运用教辅,解疑释惑) 例1变式: 1、学校门口的栏杆如图所示,栏杆从水平位置BD绕点0旋转到AC位置,已知AB⊥BD,CD⊥BD,40=4 m,AB=1.6m,C0=1 m,则栏杆C端应下降的垂直距离CD为 m (练习册变式训练1) 2.如图,2 m长的竹竿竖直放置,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同--点。此时竹竿与这一-点相距5m,与树相距10m,则树的高度为 m. 3.如图,一位测量人员要测量池塘的宽 度AB,他过A,B两点画两条相交于点0的射线,在射线上取D,E两点,使 3.若测得DE=37.2 m,他能求出A,B之间的距离吗 若能,请你帮他算出来;若不能,请你帮他设计-一个可行方案. (练习册变式训练4) 课堂小结:《练习册》 “方法归纳”。 方法归纳 1.利用相似三角形解决实际问题的核心是构造相似三角形,在构造的三角形中被测物体的高或宽是其中- -边. 2.对于相似三角形的应用,正确地识别图形是解题的关键.根据相似三角形的性质得方程或方程组,然后解方程或方程组即可得到结论. 二、课堂展示、体系建构(例题展示,变式操练) 1、会规范快速求解 2、准确说清解题依据; 会规范快速求解 2、掌握解题技巧。 1.开动脑筋,快速求解 2.规范解题格式。 将课堂小结的知识点在课本上做好简要笔记。 课堂中阶段通过变式训练,进一步巩固所学,拓展知识,为当堂测评高过关率作好充分的铺垫。进一步规范解题格式,探索解题思想方法,归纳所学,建构认知体系。
测评分享 三、监测反馈、辅导调整 1、当堂测评:《白册子》:1、2、3、4、5(每题20分,共100分),附加题:6(50分) 课堂巡视,了解检测情况。 兴趣信心、互助提升 1、独立作答 2、组间交换批阅 3、组内同学“一帮一” 课堂后阶段通过当堂测评反馈教学效果。
作业 1、预习作业:认真阅读教材第40-41页例6,铅笔勾画重点、疑点;完成《练习册》例1、例2; 2、课后作业:教材43页9题;(2)《白册子》7---13题。
反思
课题 27.2.3 相似三角形的应用(第二课时)
上课教师 上课时间 第 周 第 节
教学 目标 1.进一步巩固相似三角形的相关知识. 2.能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题.测量河宽问题、盲区问题)等的一些实际问题. 3.通过把实际问题转化成与相似三角形有关的数学模型,进-一步了解数学建模思想,培养学生分析问题、解决问题的能力.
教学 重点 运用两个三角形相似解决实际问题
教学 难点 在实际问题中建立数学模型
教 学 过 程
环节 教师活动 学生活动 设计意图
课前预习 1.布置学生的课前预习任务; 2.进行预习方法指导; 3.对学生预习任务进行检查与评定。 1、认真阅读教材40---41页例6,用铅笔勾画重点、疑点; 2、完成《练习册》例1、例2。 培养学生课前预习习惯,提升学生自主学习能力。
自主学习 理解新知 师生互动、引问激思 1、知识点一:利用影长、平面镜测量物体高度 例1如图,小颍为测量学校旗杆AB的高度,她在E处放置-块镜子.然后退到C处站立.刚好从镜子中看到旗杆的顶部B.已知小颖的眼睛D 离地面的高度CD=1.5 m,她离镜子的水平距离CE =0.5 m,镜子E离旗杆的底部A处的距离AE=2 m,且A,C,E三点在同-水平直线上,则旗杆AB的高度为( ) A.4.0 m B.4.8 m C.5.5 m D.6 m(练习册例1) 例2 如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC =2 m,BD =2.1m.如果小明眼睛距地面高度BF=DG=1. 6 m,试确定楼的高度OE.(练习册例2) 2、知识点二:相似三角形在实际问题中的应用 例3如图. 在相对的两栋楼中间有一堵墙,甲.乙两人分别在这两栋楼内观察这堵墙.视线如图①所示根据实际情况画出平而图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以 看到点G处,乙从点E可以看到点D处,点B是 DF的中点,墙AB高5.5 m,DF=100 m, BG=10.5 m.求甲,乙两人的观测点到地面的距离之差(结果精确到0.1 m)(练习册例3) 一、进入情境、领会所学(理解教材,领悟新知) 1、分小组分享例1、例2解答; 2、在课本上用红色笔勾画标记解决问题的过程,体会实际问题中建立数学模型思想。 1、分小组展示例3解答; 2、说出解题原因; 3、规范书写例题解答格式。 课堂前阶段通过师生互动,学生温故知新,领会利用三角形的相似,如何解决一些不能直接测量的物体的长度的问题。 类比例1,修订不规范解答,为后续变式练习作铺垫。 利用相似三角形解决实际问题的核心是构造 相似三角形,在构造的三角形中被测物体的高或宽是其中一边.
互动交流 巩固所学 二、点导评析、归类拓展(运用教辅,解疑释惑) 例1变式: 1.如图是小明设计用手电简来测量某古城墙高度的示意图.在地面上点P处放一-水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD, CD⊥BD,且测得AB=1.2 m,BP=1.8m,PD= 18 m,那么古城墙的高度是( ) A.6m B.8m C.12m D.24m(练习册变式训练1) 2.某小组想利用镜子与皮尺测量大树AB的高 度,因大树底部有障碍物,无法直接测量到大树底部的距离.小颍借鉴《海岛算经》的测量方法设计出如图所示的测量方案:测量者站在点F处,将镜子放在点M处时.刚好看到大树的顶端,沿大树方向向前走2.8 m,到达点D处.将镜子放在点N处时.刚好看到大树的顶端(点F.M,D,N,B在同一条直线上).若测得FM =1.5 m,DN=1.1 m,测量者眼睛到地面的距离为1.6 m,求大树AB的高度.(练习册变式训练2) 3.如图,为了估计河的寬度,在河的对岸选定 一个目标点P,在近岸取点Q和S.使点P,Q.S在一条直线上,且直线PS与河岸垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60 m,ST=120m,QR=80m,则河的宽度PQ为( )(练习册变式训练3) A.40m B.60m C.120m D. 180 m . 课堂小结:《练习册》 “方法归纳”。 方法归纳 1.对于相似三角形的应用,解题的关键是从实际问题中找出相似三角形.可借助标杆或直尺,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度. 2.可利用影长测量物体的高度,利用相似测量河的宽度(测量距离).解题的关键是根据实际问题抽象出几何图形,再利用相似三角形知识解题,要注意数形结合思想的应用. 二、课堂展示、体系建构(例题展示,变式操练) 会规范快速求解 2、准确说清解题依据; 会规范快速求解 2、掌握解题技巧。 1.开动脑筋,快速求解 2.规范解题格式。 将课堂小结的知识点在课本上做好简要笔记。 课堂中阶段通过变式训练,进一步巩固所学,拓展知识,为当堂测评高过关率作好充分的铺垫。进一步规范解题格式,探索解题思想方法,归纳所学,建构认知体系。
测评分享 三、监测反馈、辅导调整 1、当堂测评:《白册子》:1、2、3、4、5(每题20分,共100分),附加题:6(50分) 2.课堂巡视,了解检测情况。 三、兴趣信心、互助提升(满意高分,组间争雄) 独立作答 组间交换批阅 3、组内同学“一帮一” 及时解决存在问题
作业 预习作业:认真阅读教材第47-48页内容,铅笔勾画重点、疑点;完成《练习册》例1、例2; 课后作业:(1)教材43页10题;(2)《白册子》7---13题。
反思
