5.2弧、弦、圆心角

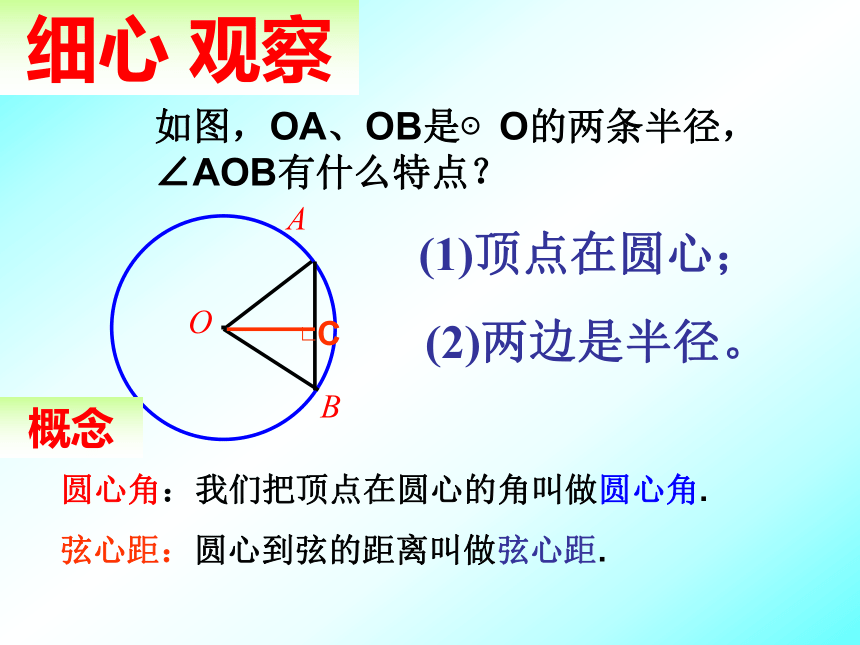
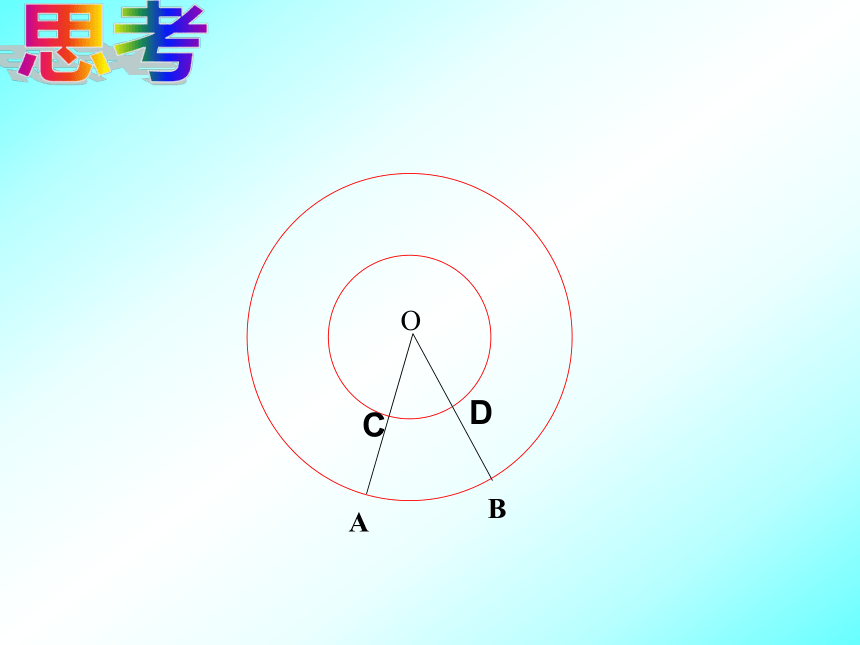
课件31张PPT。5.2 弧、弦、圆心角细心 观察如图，OA、OB是⊙O的两条半径，∠AOB有什么特点？(1)顶点在圆心；(2)两边是半径。弦心距：圆心到弦的距离叫做弦心距.
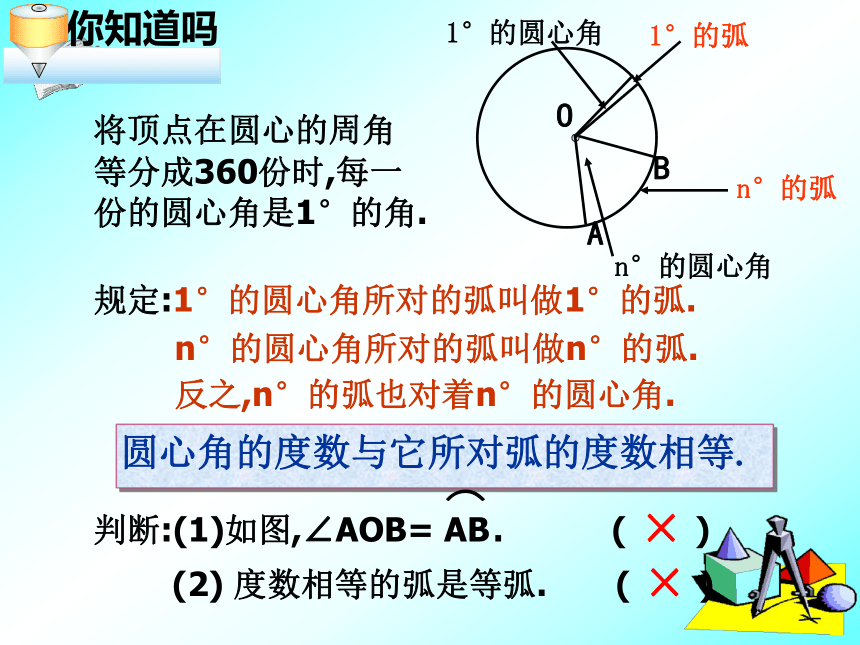
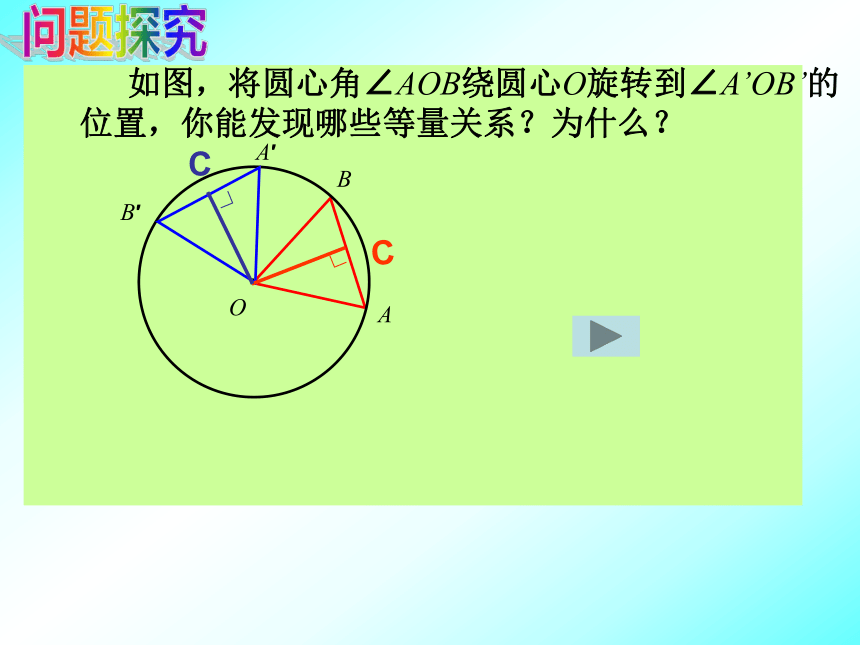
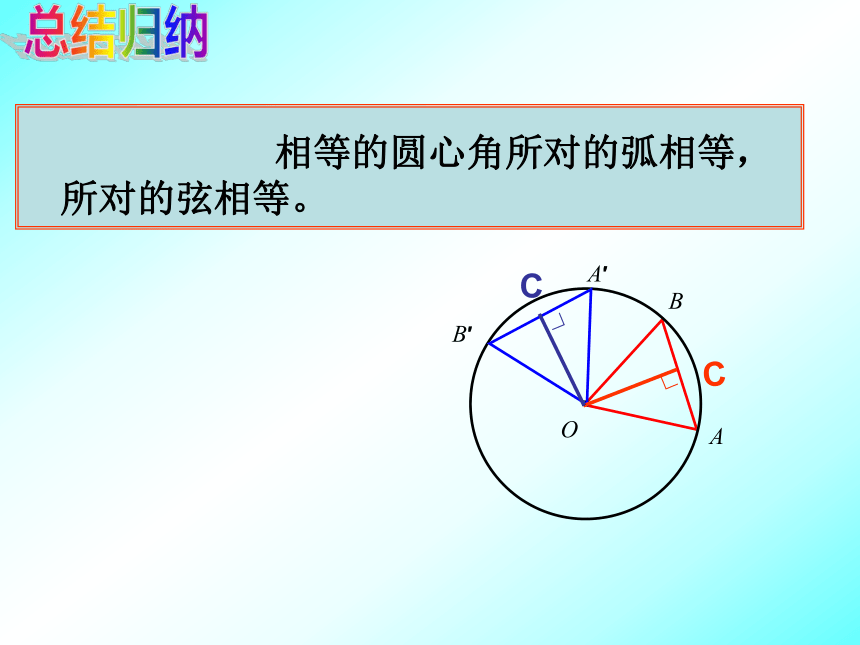
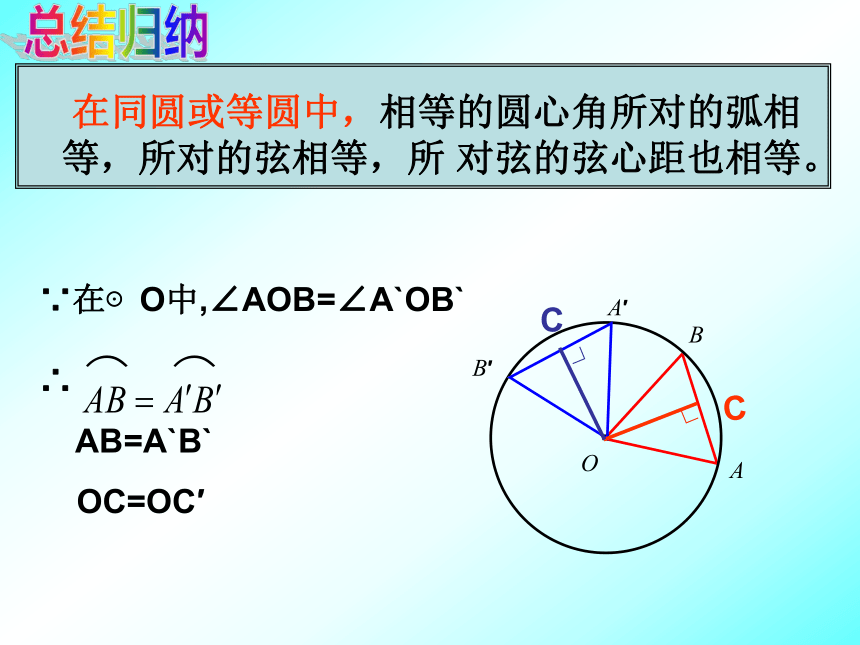
O1°的圆心角1°的弧n°的弧将顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.规定:1°的圆心角所对的弧叫做1°的弧.n°的圆心角所对的弧叫做n°的弧.反之,n°的弧也对着n°的圆心角.(2) 度数相等的弧是等弧. ( )×× 如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？问题探究 相等的圆心角所对的弧相等，所对的弦相等。总结归纳思考总结归纳∴
AB=A`B`
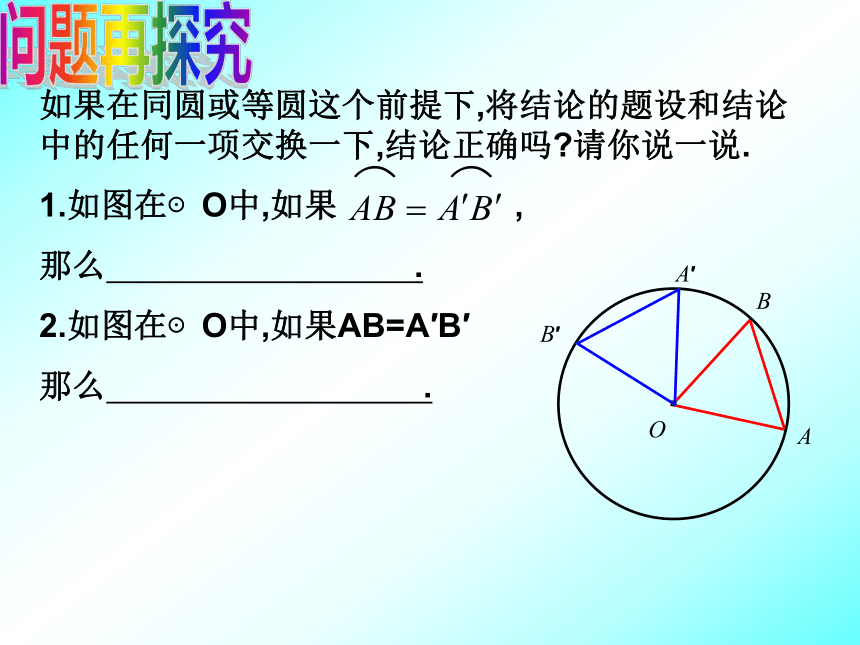
OC=OC′∵在⊙O中,∠AOB=∠A`OB`·OABA′B′问题再探究如果在同圆或等圆这个前提下,将结论的题设和结论中的任何一项交换一下,结论正确吗?请你说一说.
1.如图在⊙O中,如果 ,
那么 .
2.如图在⊙O中,如果AB=A′B′
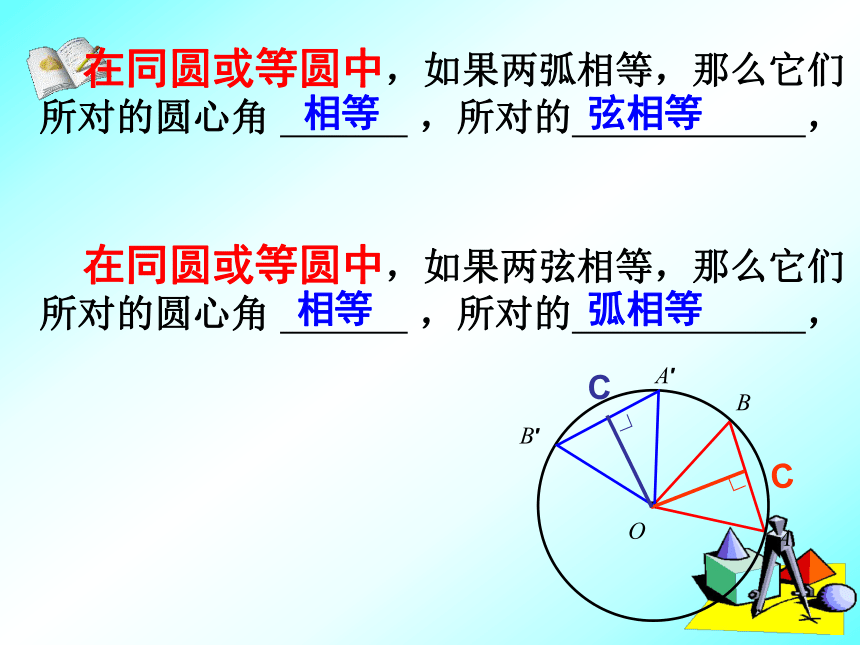
那么 . 在同圆或等圆中，如果两弧相等，那么它们所对的圆心角 ，所对的 ， 在同圆或等圆中，如果两弦相等，那么它们所对的圆心角 ，所对的 ，相等弦相等相等弧相等(1)圆心角
(2)圆心角所对的弧
(3)圆心角所对的弦
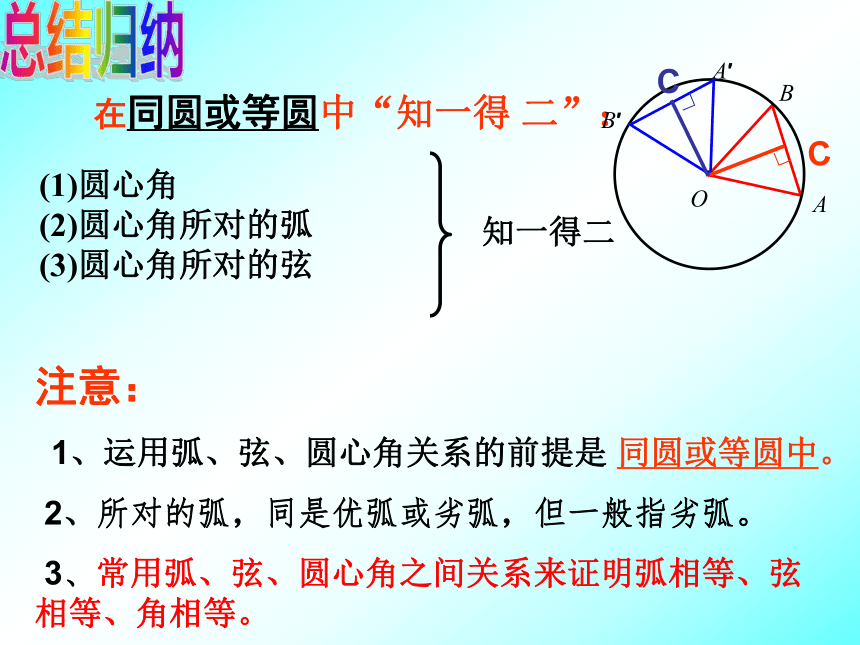
知一得二在同圆或等圆中“知一得 二”：总结归纳注意：
1、运用弧、弦、圆心角关系的前提是 同圆或等圆中。
2、所对的弧，同是优弧或劣弧，但一般指劣弧。
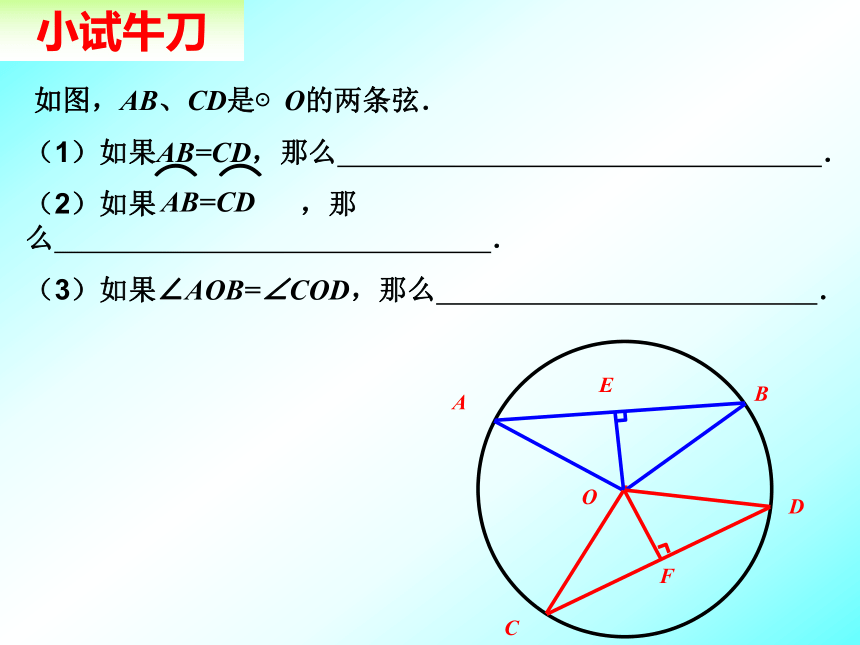
3、常用弧、弦、圆心角之间关系来证明弧相等、弦相等、角相等。 如图，AB、CD是⊙O的两条弦．
（1）如果AB=CD，那么 ．
（2）如果 ，那么 ．
（3）如果∠AOB=∠COD，那么 ．
小试牛刀AB=CD⌒⌒2.下列说法正确的是（ ）
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心角相等，所对的弦相等
D.弦相等所对的圆心角相等 B例题1变:如图,在⊙O中,∠AOC=∠BOC,
(1)∠ABC与∠BAC相等吗?为什么?(2)在图中,你还能得到哪些结论?(3)请你添加一个条件,使四边形OACB成为菱形.E1、如图，AB是⊙O 的直径， ∠COD=35°，求∠AOE 的度数．解：练习BC=CD=DE⌒⌒⌒∵2、AB为直径，AD=DC=BC,则∠CBA= .O 3、在⊙O中，已知AB = 2CD , 则弦AB与2CD的大小关系为 。⌒⌒4、在三个等圆上各有一条劣弧AB、CD、EF，如果AB + CD = EF ,那么AB + CD 与 EF 的关系是（ ）⌒⌒⌒⌒⌒⌒A AB + CD = EFB AB + CD > EFC AB + CD < EFD 不能确定应用新知OABCD例2 已知：如图，在⊙O中，AD=BC。
求证：AB=CD。⌒⌒已知：如图，在⊙O中，AD=BC。
求证：AB=CD。OABCD变式1：变式2：已知：如图，在⊙O中，AB=CD。
求证：AD=BC。OABCD变式3：已知：如图，在⊙O中，AB=CD。
求证：∠AOD=∠BOC。OABCD1.如图，AB是⊙O的直径，AC是弦， OD∥AC.
求证：BD=CD⌒⌒ABCDOABCDMN2.如图，AB,CD是⊙O的弦，点M,N分别为AB,CD的中点，且∠AMN=∠CNM
求证：AB=CD．O感悟与收获谈谈你这节课的收获？你对圆的对称性有什么认识？1、圆具有旋转不变性，中心对称性是它的特例.2、在同圆或等圆中,圆心角、弦、弧具有下列关系：转化1、在⊙O与⊙O`中，若∠AOB=∠A`O`B` , 则有（ ）D AB、A`B`大小无法比较⌒⌒巩固练习： 2、在同圆中，圆心角∠AOB= 2∠COD，则两条弧AB与CD的关系是（ ）⌒⌒ D 不能确定3，如果圆中弦长恰好等于半径长，那么这条弦所对的圆心角是______.
4.若一条弦把圆分成1：3的两部分，则劣弧所对的圆心角为_______.5、已知AB是⊙O的直径，M，N分别是OA、OB的中点，CM⊥AB, DN⊥AB，垂足为M、N。求证：AC=BD⌒⌒OABC⌒如图，A、B、C是⊙O上的三点，且有AB=BC=CA，连接AB、BC、CA 。
(1)试确定△ABC的形状；
(2) 若AB=a，求⊙O的半径。