9.3.2用正多边形拼地版
图片预览










文档简介
课件32张PPT。9.3.2用多种正多边形拼地板复习:
1、在正三角形、正方形、正五边形、正六边形、正八边形中取一种,可以铺满地板的有哪些?
2、用同种正多边形瓷砖能不留空隙,不重叠地铺满地板的关键是什么?
模型:
正多边形个数×正多边形内角度数=360o
正三角形、正方形、正六边形围绕一点拼在一起的正多边形的内角之和为360o 学习目标理解多种正多边形能够铺满地面的道理.
欣赏丰富多彩的图案,提高审美情趣.
了解即使满足“围绕一点拼在一起的几种正多边形的内角之和为一个圆周”的条件,也不一定能铺满地面.
自学提示阅读教材,思考下列问题:
1.你知道有哪几种正多边形在一起能够拼成一个平面图形?这些正多边形在一起能够拼成一个平面图形的理由是什么?
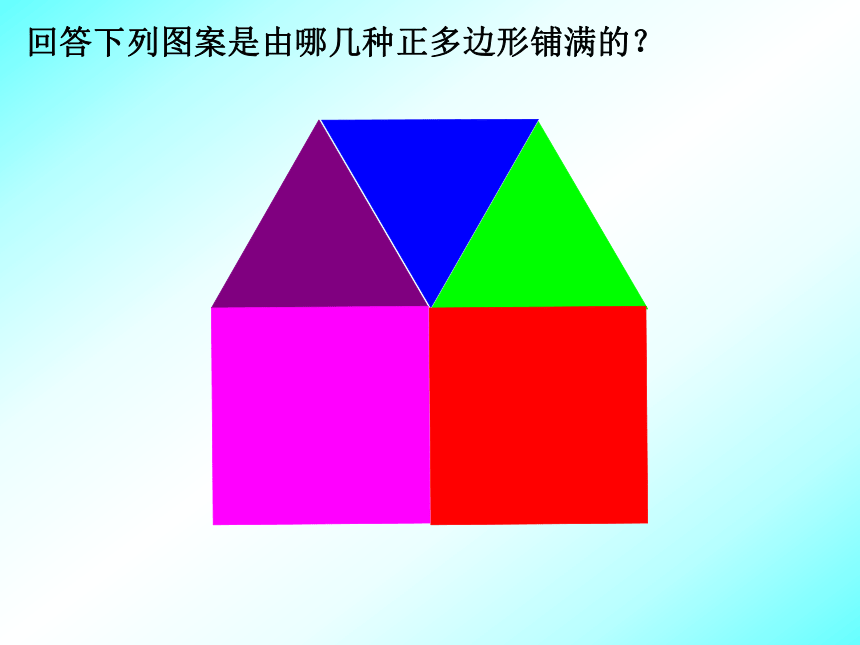
2.几个正多边形只要能够拼成一个平面图形,是不是一定能够铺满地面?你能举例说明吗?回答下列图案是由哪几种正多边形铺满的? 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形中任取两种进行组合是否能铺满地面呢?正方形、正三角形正六边形、正三角形正六边形、正方形、正三角形正十二边形、正三角形正八边形、正方形小结:如果几个多边形的内角加在一起恰好能组成一个周角的话,它们就能够拼成一个平面图形。
正五边形、正十边形围绕一点能拼成360o,但能扩展到整个平面,即铺满地面吗?尽管能围绕一点拼成360o,但不能扩展到整个平面。正十二边形、正方形、正六边形正十二边形、正方形、正三角形两种正多边形拼地板:围绕 一点拼在一起的两种正多边形的
内角之和为360o。关键:模型:
正多边形1个数×正多边形1内角度数 +
正多边形2个数×正多边形2内角度数=360 o
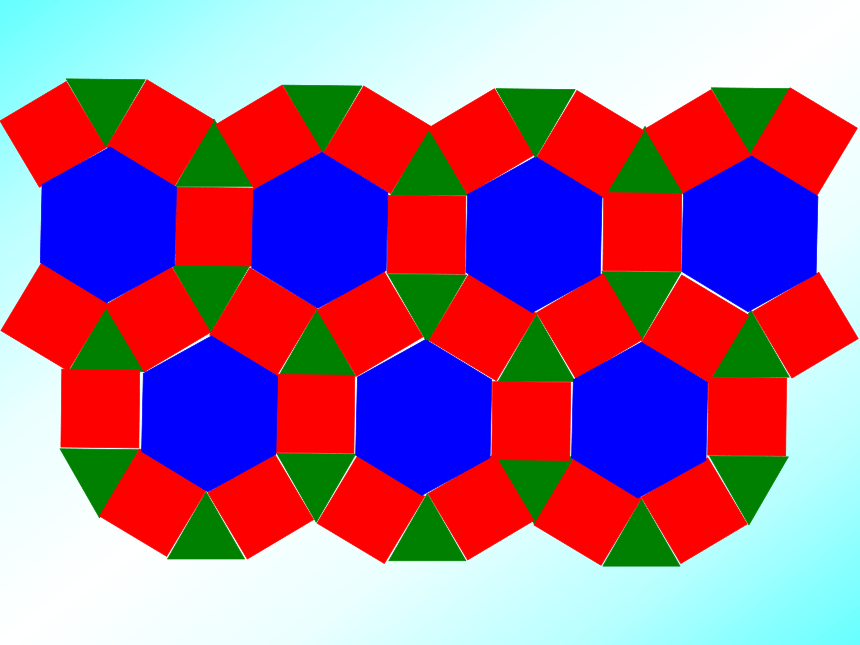
观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。小结 如果几个多边形的内角加在一起恰好
组成一个周角的话,它们就能够拼成一个
平面图形。
注意:有时几种正多边形的组合能围绕一点拼成
周角,但不能扩展到整个平面,即不能铺
满平面。如:正五边形与正十边形的组合。作业用多种正多边形拼用同种正多边形拼地板,你知道有哪几种正多边形可以铺满地面?
地板,你能设计出与本节所见到的不一样的图案吗?
用多种正多边形拼地板,你知道有哪几种正多边形可以铺满地面? 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。
2、用同种正多边形瓷砖能不留空隙,不重叠地铺满地板的关键是什么?
模型:
正多边形个数×正多边形内角度数=360o
正三角形、正方形、正六边形围绕一点拼在一起的正多边形的内角之和为360o 学习目标理解多种正多边形能够铺满地面的道理.
欣赏丰富多彩的图案,提高审美情趣.
了解即使满足“围绕一点拼在一起的几种正多边形的内角之和为一个圆周”的条件,也不一定能铺满地面.
自学提示阅读教材,思考下列问题:
1.你知道有哪几种正多边形在一起能够拼成一个平面图形?这些正多边形在一起能够拼成一个平面图形的理由是什么?
2.几个正多边形只要能够拼成一个平面图形,是不是一定能够铺满地面?你能举例说明吗?回答下列图案是由哪几种正多边形铺满的? 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形中任取两种进行组合是否能铺满地面呢?正方形、正三角形正六边形、正三角形正六边形、正方形、正三角形正十二边形、正三角形正八边形、正方形小结:如果几个多边形的内角加在一起恰好能组成一个周角的话,它们就能够拼成一个平面图形。
正五边形、正十边形围绕一点能拼成360o,但能扩展到整个平面,即铺满地面吗?尽管能围绕一点拼成360o,但不能扩展到整个平面。正十二边形、正方形、正六边形正十二边形、正方形、正三角形两种正多边形拼地板:围绕 一点拼在一起的两种正多边形的
内角之和为360o。关键:模型:
正多边形1个数×正多边形1内角度数 +
正多边形2个数×正多边形2内角度数=360 o
观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。小结 如果几个多边形的内角加在一起恰好
组成一个周角的话,它们就能够拼成一个
平面图形。
注意:有时几种正多边形的组合能围绕一点拼成
周角,但不能扩展到整个平面,即不能铺
满平面。如:正五边形与正十边形的组合。作业用多种正多边形拼用同种正多边形拼地板,你知道有哪几种正多边形可以铺满地面?
地板,你能设计出与本节所见到的不一样的图案吗?
用多种正多边形拼地板,你知道有哪几种正多边形可以铺满地面? 观察下面这些瓷砖的图案,分别说出它们是由哪些图形构成,以及它们能铺满地面的理由?。
