18.2.3正方形同步练习2021-2022学年人教版八年级数学下册(word,有答案)
文档属性
| 名称 | 18.2.3正方形同步练习2021-2022学年人教版八年级数学下册(word,有答案) | 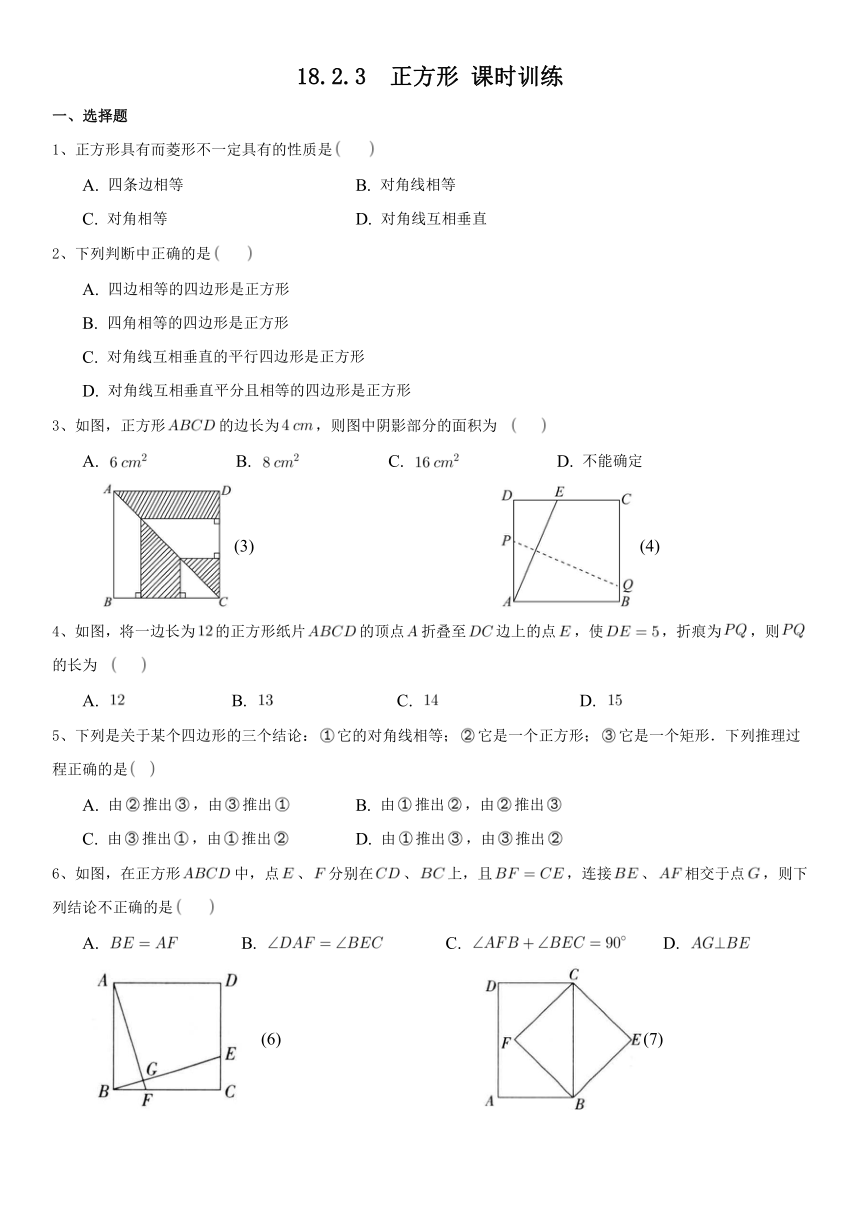 | |
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-31 22:17:00 | ||
图片预览


文档简介
18.2.3 正方形 课时训练
一、选择题
1、正方形具有而菱形不一定具有的性质是
A. 四条边相等 B. 对角线相等
C. 对角相等 D. 对角线互相垂直
2、下列判断中正确的是
A. 四边相等的四边形是正方形
B. 四角相等的四边形是正方形
C. 对角线互相垂直的平行四边形是正方形
D. 对角线互相垂直平分且相等的四边形是正方形
3、如图,正方形的边长为,则图中阴影部分的面积为
A. B. C. D. 不能确定
(3) (4)
4、如图,将一边长为的正方形纸片的顶点折叠至边上的点,使,折痕为,则的长为
A. B. C. D.
5、下列是关于某个四边形的三个结论:它的对角线相等;它是一个正方形;它是一个矩形.下列推理过程正确的是
A. 由推出,由推出 B. 由推出,由推出
C. 由推出,由推出 D. 由推出,由推出
6、如图,在正方形中,点、分别在、上,且,连接、相交于点,则下列结论不正确的是
A. B. C. D.
(6) (7)
7、如图,在矩形内有一点,与分别平分和,点为矩形外一点,连接,现添加下列条件:
,;
,;
,;
,,
其中能判定四边形是正方形的共有
A. 个 B. 个 C. 个 D. 个
8、有一边长为的正方形纸片,先将正方形对折,设折痕为如下图,再沿过点的折痕将角翻折,使得点落在的上如下图,折痕交于点,则的长度为
A. B. C. D.
9、如图,正方形中,点在上,,,垂足分别为、,,则的长为
A. B. C. D.
10、如图,在正方形中,,点,分别在边,上,若将四边形沿折叠,点恰好落在边上,则的长度为
A. B. C. D.
(9) (10)
二、填空题
11、为正方形对角线上一点,且,则_______度.
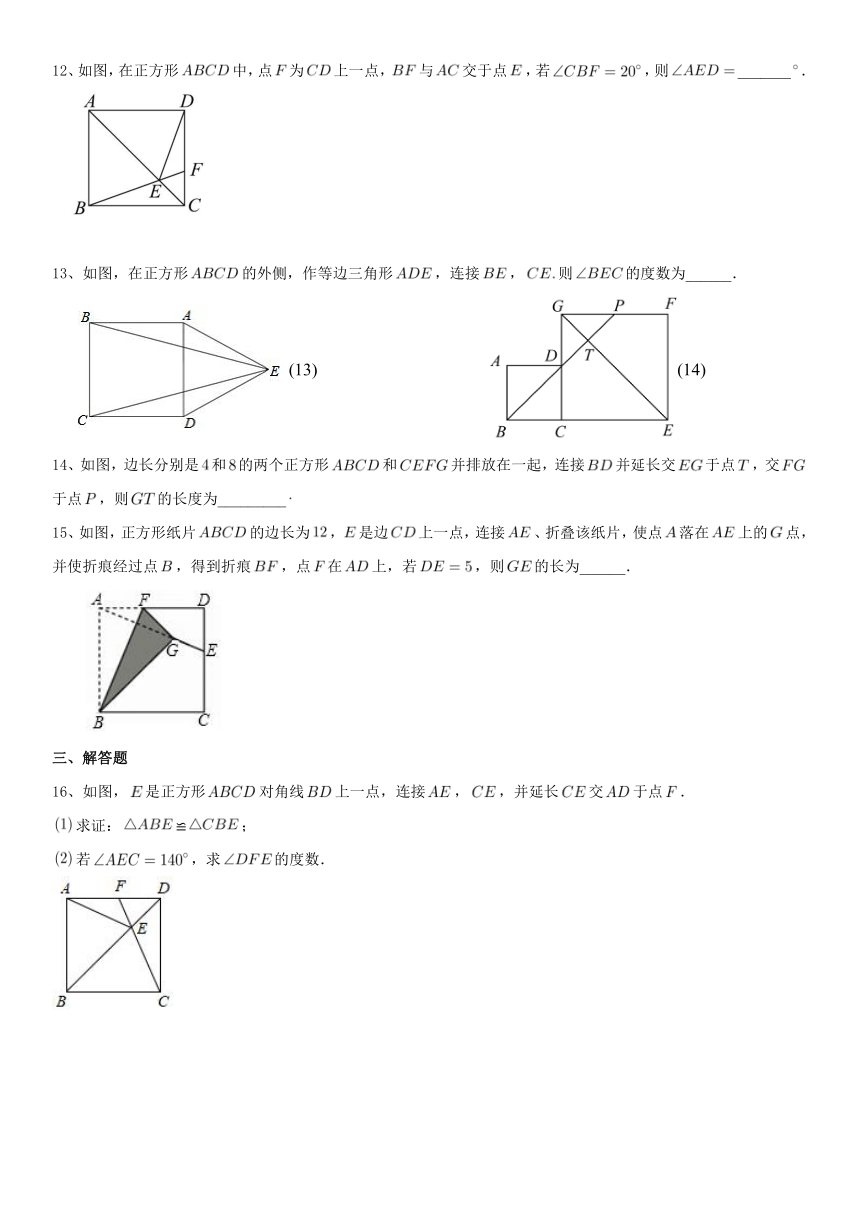
12、如图,在正方形中,点为上一点,与交于点,若,则_______.
13、如图,在正方形的外侧,作等边三角形,连接,则的度数为______.
(13) (14)
14、如图,边长分别是和的两个正方形和并排放在一起,连接并延长交于点,交于点,则的长度为_________
15、如图,正方形纸片的边长为,是边上一点,连接、折叠该纸片,使点落在上的点,并使折痕经过点,得到折痕,点在上,若,则的长为______.
三、解答题
16、如图,是正方形对角线上一点,连接,,并延长交于点.
求证:≌;
若,求的度数.
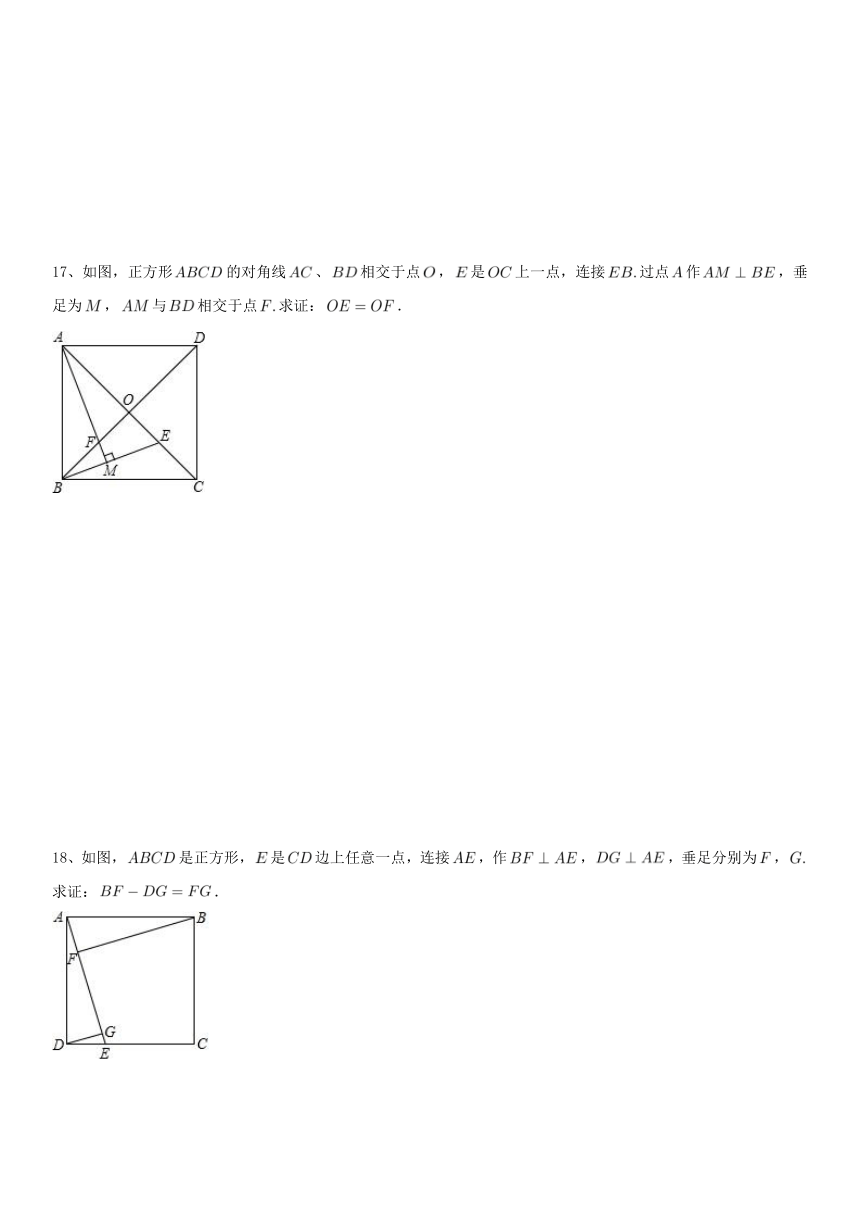
17、如图,正方形的对角线、相交于点,是上一点,连接过点作,垂足为,与相交于点求证:.
18、如图,是正方形,是边上任意一点,连接,作,,垂足分别为,求证:.
19、已知:如图,在正方形中,对角线,相交于点,点,分别是边,上的点,且.
求证:.
20、如图,在正方形中,点,分别在,上,且.
试探索线段,的大小关系,写出你的结论并说明理由;
连接,,分别取,,,的中点,,,,顺次连接,得到四边形:
请在图中补全图形;
四边形是什么特殊平行四边形?请说明理由.
答案和解析
选择题
1-10
二、填空题
11、
12、
13、
14、
15、
三、解答题
16、证明:四边形是正方形,
,,,
在和中,,≌;
≌,,
又,,
,,
,.
17、证明:四边形是正方形.,.
又,,
.≌..
18、证明:四边形是正方形,,,
,,,
,
,
在和中,
≌,
,,
,
,
.
19、解:四边形为正方形,
,,,
,即,
,
≌,
.
20、解:.
四边形是正方形,
,,
又,≌..
画出图形如下图所示:
四边形是正方形.
理由如下:
,,,分别是,,,的中点,
,.
,
.
四边形是菱形.
≌,.
,..
又,,
.
四边形是正方形.
一、选择题
1、正方形具有而菱形不一定具有的性质是
A. 四条边相等 B. 对角线相等
C. 对角相等 D. 对角线互相垂直
2、下列判断中正确的是
A. 四边相等的四边形是正方形
B. 四角相等的四边形是正方形
C. 对角线互相垂直的平行四边形是正方形
D. 对角线互相垂直平分且相等的四边形是正方形
3、如图,正方形的边长为,则图中阴影部分的面积为
A. B. C. D. 不能确定
(3) (4)
4、如图,将一边长为的正方形纸片的顶点折叠至边上的点,使,折痕为,则的长为
A. B. C. D.
5、下列是关于某个四边形的三个结论:它的对角线相等;它是一个正方形;它是一个矩形.下列推理过程正确的是
A. 由推出,由推出 B. 由推出,由推出
C. 由推出,由推出 D. 由推出,由推出
6、如图,在正方形中,点、分别在、上,且,连接、相交于点,则下列结论不正确的是
A. B. C. D.
(6) (7)
7、如图,在矩形内有一点,与分别平分和,点为矩形外一点,连接,现添加下列条件:
,;
,;
,;
,,
其中能判定四边形是正方形的共有
A. 个 B. 个 C. 个 D. 个
8、有一边长为的正方形纸片,先将正方形对折,设折痕为如下图,再沿过点的折痕将角翻折,使得点落在的上如下图,折痕交于点,则的长度为
A. B. C. D.
9、如图,正方形中,点在上,,,垂足分别为、,,则的长为
A. B. C. D.
10、如图,在正方形中,,点,分别在边,上,若将四边形沿折叠,点恰好落在边上,则的长度为
A. B. C. D.
(9) (10)
二、填空题
11、为正方形对角线上一点,且,则_______度.
12、如图,在正方形中,点为上一点,与交于点,若,则_______.
13、如图,在正方形的外侧,作等边三角形,连接,则的度数为______.
(13) (14)
14、如图,边长分别是和的两个正方形和并排放在一起,连接并延长交于点,交于点,则的长度为_________
15、如图,正方形纸片的边长为,是边上一点,连接、折叠该纸片,使点落在上的点,并使折痕经过点,得到折痕,点在上,若,则的长为______.
三、解答题
16、如图,是正方形对角线上一点,连接,,并延长交于点.
求证:≌;
若,求的度数.
17、如图,正方形的对角线、相交于点,是上一点,连接过点作,垂足为,与相交于点求证:.
18、如图,是正方形,是边上任意一点,连接,作,,垂足分别为,求证:.
19、已知:如图,在正方形中,对角线,相交于点,点,分别是边,上的点,且.
求证:.
20、如图,在正方形中,点,分别在,上,且.
试探索线段,的大小关系,写出你的结论并说明理由;
连接,,分别取,,,的中点,,,,顺次连接,得到四边形:
请在图中补全图形;
四边形是什么特殊平行四边形?请说明理由.
答案和解析
选择题
1-10
二、填空题
11、
12、
13、
14、
15、
三、解答题
16、证明:四边形是正方形,
,,,
在和中,,≌;
≌,,
又,,
,,
,.
17、证明:四边形是正方形.,.
又,,
.≌..
18、证明:四边形是正方形,,,
,,,
,
,
在和中,
≌,
,,
,
,
.
19、解:四边形为正方形,
,,,
,即,
,
≌,
.
20、解:.
四边形是正方形,
,,
又,≌..
画出图形如下图所示:
四边形是正方形.
理由如下:
,,,分别是,,,的中点,
,.
,
.
四边形是菱形.
≌,.
,..
又,,
.
四边形是正方形.
