第一章动量守恒定律章练习 (word版含答案)
文档属性
| 名称 | 第一章动量守恒定律章练习 (word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 351.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-31 00:00:00 | ||
图片预览


文档简介
汽开三中高二物理动量章练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
一个质量为0.18kg的垒球以20m/s的水平速度向右飞向球棒,被球棒打击后反向水平飞回,速度大小变为40m/s,则这一过程动量的变化量为()
A. 大小10.8kg m/s,方向向右 B. 大小10.8 kg m/s,方向向左
C. 大小3.6 kg m/s,方向向右 D. 大小3.6 kg m/s,方向向左
如图所示,两个质量相等的物体A、B从同一高度沿倾角不同的两固定光滑斜面由静止自由滑下,在到达斜面底端的过程中,下列说法中正确的是( )
A. 两物体所受重力的冲量相同
B. 两物体所受合外力的冲量相同
C. 两物体到达斜面底端时的动量不同
D. 两物体到达斜面底端时的动量水平分量相同
一个质量为0.5 kg的小钢球竖直下落,落地时速度大小为1m/s,与地面作用0.1s后以等大的动量被反弹。小钢球在与地面碰撞的过程中,下列说法中正确的是()
A. 小钢球重力的冲量是0.1 kg·m/s
B. 若选向上为正方向,则小钢球的动量变化量为-1kg·m/s
C. 若选向上为正方向,则小钢球受到的合力冲量是-1 N·s
D. 若小钢球受到的支持力不变,小钢球受到的支持力为15N
如图所示,质量为的半圆轨道小车静止在光滑的水平地面上,其水平直径长度为,现将质量也为的小球从距点正上方高处由静止释放,然后由点经过半圆轨道后从冲出,在空中能上升到距点所在水平线的最大高度为处不计空气阻力,小球可视为质点,则( )
A. 小球和小车组成的系统动量守恒
B. 小球离开小车后做斜向上抛运动
C. 小车向左运动的最大距离为
D. 小球第二次在空中能上升到距点所在水平线的最大高度为
如图所示,一个质量为m1=50 kg的人抓在一只大气球下方,气球下面有一根长绳。气球和长绳的总质量为m2=20 kg,长绳的下端刚好和水平面接触。当静止时人离地面的高度为h=5 m。如果这个人开始沿绳向下滑,当他滑到绳下端时,他离地面高度是(可以把人看作质点) ( )
A. 5 m
B. 3.6 m
C. 2.6 m
D. 8 m
如图所示,质量为的小车和质量为的滑块均静止在光滑水平面上,小车紧靠滑块(不粘连),在小车上固定的轻杆顶端系细绳,绳的末端拴一质量为m的小球,将小球向右拉至细绳水平且绷直后释放,在小球从释放至第一次达到左侧最高点的过程中,下列说法正确的是( )。
A. 小球与小车组成的系统机械能守恒
B. 小球、小车组成的系统在水平方向动量守恒
C. 小球运动至最低点时,小车和滑块分离
D. 小球一定能向左摆到释放时的高度
如图所示,质量为m的A球以速度v0在光滑水平面上运动,与原来静止的质量为4m的B球碰撞,碰撞后A球以v=av0(待定系数a<1)的速率弹回,并与挡板P发生完全弹性碰撞,若要使A球能追上B球再次相撞,则a的取值范围为( )
A. < a< B. < a< C. < a< D. < a≤
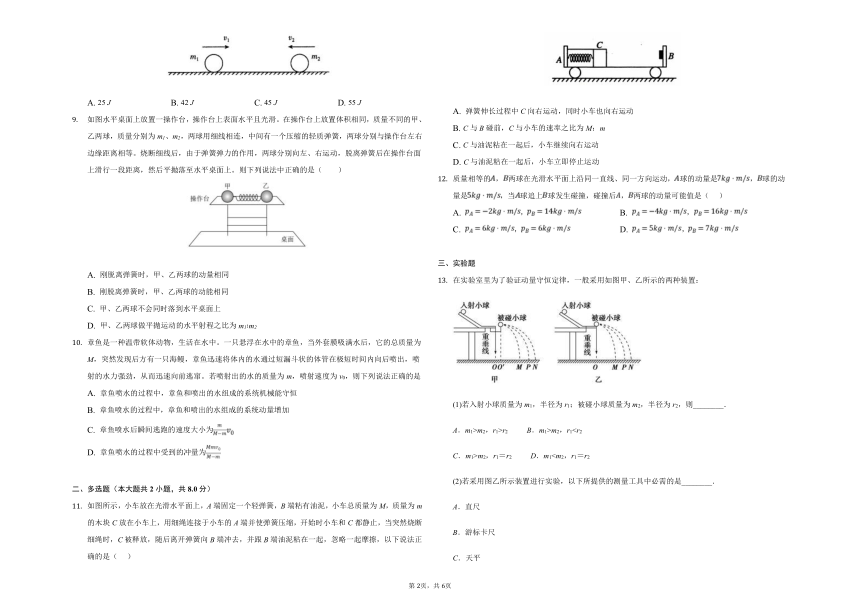
如图,两质量分别为和小球在光滑水平面上相向而行,速度大小分别为和,发生碰撞后,系统损失的机械能可能是( )
A. 25 J B. 42 J C. 45 J D. 55 J
如图水平桌面上放置一操作台,操作台上表面水平且光滑。在操作台上放置体积相同,质量不同的甲、乙两球,质量分别为m1、m2,两球用细线相连,中间有一个压缩的轻质弹簧,两球分别与操作台左右边缘距离相等。烧断细线后,由于弹簧弹力的作用,两球分别向左、右运动,脱离弹簧后在操作台面上滑行一段距离,然后平抛落至水平桌面上。则下列说法中正确的是( )
A. 刚脱离弹簧时,甲、乙两球的动量相同
B. 刚脱离弹簧时,甲、乙两球的动能相同
C. 甲、乙两球不会同时落到水平桌面上
D. 甲、乙两球做平抛运动的水平射程之比为m1∶m2
章鱼是一种温带软体动物,生活在水中。一只悬浮在水中的章鱼,当外套膜吸满水后,它的总质量为M,突然发现后方有一只海鳗,章鱼迅速将体内的水通过短漏斗状的体管在极短时间内向后喷出,喷射的水力强劲,从而迅速向前逃窜。若喷射出的水的质量为m,喷射速度为v0,则下列说法正确的是
A. 章鱼喷水的过程中,章鱼和喷出的水组成的系统机械能守恒
B. 章鱼喷水的过程中,章鱼和喷出的水组成的系统动量增加
C. 章鱼喷水后瞬间逃跑的速度大小为
D. 章鱼喷水的过程中受到的冲量为
二、多选题(本大题共2小题,共8.0分)
如图所示,小车放在光滑水平面上,A端固定一个轻弹簧,B端粘有油泥,小车总质量为M,质量为m的木块C放在小车上,用细绳连接于小车的A端并使弹簧压缩,开始时小车和C都静止,当突然烧断细绳时,C被释放,随后离开弹簧向B端冲去,并跟B端油泥粘在一起,忽略一起摩擦,以下说法正确的是( )
A. 弹簧伸长过程中C向右运动,同时小车也向右运动
B. C与B碰前,C与小车的速率之比为M:m
C. C与油泥粘在一起后,小车继续向右运动
D. C与油泥粘在一起后,小车立即停止运动
质量相等的,两球在光滑水平面上沿同一直线、同一方向运动,球的动量是,球的动量是,当球追上球发生碰撞,碰撞后,两球的动量可能值是( )
A. , B. ,
C. , D. ,
三、实验题
在实验室里为了验证动量守恒定律,一般采用如图甲、乙所示的两种装置:
(1)若入射小球质量为m1,半径为r1;被碰小球质量为m2,半径为r2,则________.
A.m1>m2,r1>r2 B.m1>m2,r1C.m1>m2,r1=r2 D.m1(2)若采用图乙所示装置进行实验,以下所提供的测量工具中必需的是________.
A.直尺
B.游标卡尺
C.天平
D.弹簧测力计
E.秒表
(3)设入射小球的质量为m1,被碰小球的质量为m2,则在用图甲所示装置进行实验时(P为碰前入射小球落点的平均位置),所得“验证动量守恒定律”的结论为______________.(用装置图中的字母表示)
四、计算题
如图所示,在光滑水平面上有两个木块A、B,木块B左端放置小物块C并保持静止,已知,,现木块A以初速度沿水平方向向右滑动,木块A与B相碰后具有共同速度但不粘连,C与A、B间均有摩擦.求:
木块A与B相碰瞬间A木块及小物块C的速度大小;
设木块A足够长,求小物块C的最终速度.
如图所示,光滑水平面上有一质量为2M、半径为R(R足够大)的圆弧曲面C,质量为M的小球B置于其底端,另一个小球A质量为,以v0=6m/s的速度向B运动,并与B发生弹性碰撞,不计一切摩擦,小球均视为质点,求:
(1)小球B的最大速率;
(2)小球B运动到圆弧曲面最高点时的速率;
(3)通过计算判断小球B能否与小球A再次发生碰撞。
答案和解析
1.【答案】B
规定水平向右为正方向,则初动量p1=mv1=0.18kg×20m/s=3.6kg m/s;
打击后动量为:p2=mv2=0.18kg×(-40m/s)=-7.2kg m/s;
故动量变化为:△p=p2-p1=-10.8kg m/s,负号表示方向与规定的正方向相反,即向左;
故选B。
2.【答案】C
解:物体在下滑中只有重力做功,而重力做功只与高度差有关,故两种情况下重力做功相等,由mgh=mv2得两种情况下到达斜面底端的速度的大小是相等的;
A、两种情况下到达斜面底端的速度的大小是相等,又因长的斜面倾角小,物体的加速度小,所以斜面越长下滑的时间越长,所以两种情况下重力作用的时间不相等,重力的冲量也不相等.故A错误;
B、物体在两种情况下到达斜面底端的速度的大小是相等的,而速度的方向不同,所以两种情况下物体的末动量不同.根据动量定理:I=△P=mv-0,所以合力的冲量大小相等,方向是不同的.故B错误;
C、物体在两种情况下到达斜面底端的速度的大小是相等的,方向不同,所以两物体到达斜面底端时的动量不同.故C正确;
D、物体在两种情况下到达斜面底端的速度的大小是相等的,而速度的方向不同,所以两物体到达斜面底端时的动量水平分量不同.故D错误.
故选:C
3.【答案】D
A.根据冲量的定义可知:,故 A错误;
B.若选向上为正方向,则小钢球的动量变化量为,故B错误;
C.根据动量定理,合力冲量等于动量的变化量,所以若选向上为正方向,则小钢球受到的合力冲量是,故 C错误;
D.若选向上为正方向,根据动量定理可得:,解得:,故D正确。
4.【答案】C
A.小球与小车组成的系统在水平方向不受外力,水平方向系统动量守恒,竖直方向小球有加速度,所以系统整体所受合外力不为零,系统动量不守恒,故A错误;
B.小球与小车组成的系统在水平方向动量守恒,小球由B点离开小车时系统水平方向动量为零,小球与小车水平方向速度为零,小球离开小车后做竖直上抛运动,故B错误;
C.设小车向左的最大距离为x,系统水平方向动量守恒,以向右为正方向,在水平方向,由动量守恒定律得:,即,解得,,故C正确;
D.小球第一次车中运动过程中,由动能定理得:,Wf为小球克服摩擦力做功大小,解得:,即小球第一次在车中滚动损失的机械能为:,由于小球第二次在车中滚动时,对应位置处速度变小,因此小车给小球的弹力变小,摩擦力变小,摩擦力做功小于,机械能损失小于,因此小球再次离开小车时,能上升的高度大于:,而小于,故D错误。
5.【答案】B
设人的速度v1,气球的速度v2,根据人和气球动量守恒得
则m1v1=m2v2,
所以v1=v2,
气球和人运动的路程之和为h=5m,则s1=m,s2=m,
即人下滑m,气球上升m,
所以人离地高度为m,约等于3.6m。故B正确,ACD错误。
故选:B。
6.【答案】C
A.对小球、小车和滑块组成的系统,只有重力做功,机械能守恒,因为在整个过程中滑块获得了动能,则小球和小车组成的系统机械能不守恒,故A错误;
B.对小球、小车和滑块组成的系统,在水平方向上不受外力,则在水平方向上动量守恒,小球、小车组成的系统在水平方向动量不守恒,故B错误;
C.小球向左摆到最低点的过程中,速度增大,水平方向上的动量增大,根据动量守恒定律,小车和滑块向右的动量增大,可知向右的速度增大,小球从最低点向左摆时,速度减小,水平方向上的动量减小,则小车向右的动量减小,速度减小,与滑块发生分离,C正确;
D.小球、小车和滑块组成的系统在水平方向上动量守恒,最终滑块的速度不为零,则当小球向左摆到最高点时,水平速度不为零,根据机械能守恒定律知,小球不能摆到释放时的高度,故D错误。
7.【答案】D
A、B碰撞过程中,以v0方向为正方向,根据动量守恒定律得:mv0=-m av0+4mvB
A与挡板P碰撞后能追上B发生再碰的条件是:av0>vB,解得a>
碰撞过程中损失的机械能△E=mv02-[m(av0)2+mvB2]≥0,解得a≤。
所以a满足的条件是<a≤.故ABC错误,D正确。
故选D。
8.【答案】A
当两球发生完全非弹性碰撞时,根据动量守恒有:m1v1-m2v2=(m1+m2)v
解得:v==-4m/s
则损失的最大机械能△E=m1v12+m2v22 (m1+m2)v2=40J
故A正确,BCD错误。
故选A
9.【答案】C
A.取向左为正方向,由动量守恒定律得:p甲+p乙=0,得p甲=-p乙,则刚脱离弹簧时,甲、乙两球的动量大小相等,方向相反,动量不同,故A错误;
B.刚脱离弹簧时,甲、乙两球的动能之比为==,动能不同,故B错误;
C.根据p=mv知,刚脱离弹簧时,甲、乙两球的动量大小相等,质量不同,则刚脱离弹簧时,甲、乙两球的速度大小不等,两球分别与操作台左右边缘距离相等,则两球离开弹簧后在操作台运动的时间不等。两球离开操作台后做平抛运动,两球平抛运动下落的高度相同,则两球平抛运动的时间相同,所以两球不会同时落到水平桌面上,故C正确;
D.甲、乙两球做平抛运动的初速度大小之比v1:v2=||:||=m2:m1,甲、乙两球做平抛运动的水平射程之比为x1:x2=v1t:v2t=m2:m1,故D错误。
故选:C。
10.【答案】C
A、在章鱼喷水的过程中,章鱼的生物能转化为机械能,系统机械能增加,A项错误;
B、章鱼喷水过程所用的时间极短,内力远大于外力,章鱼和喷出的水组成的系统动量守恒,B项错误;
C、由动量守恒定律得0=(M-m)v-,可得章鱼喷水后瞬间逃跑的速度大小为v=,C项正确;
D、章鱼喷水的过程中受到的冲量大小等于喷出的水的动量大小,D项错误。
11.【答案】BD
A.小车与木块C以及弹簧组成的系统在水平方向上动量守恒,C向右运动时,小车应向左运动,故A错误.
B.设碰前C的速率为v1,小车的速率为v2,则0=mv1-Mv2,得=,故B正确.
CD.设C与油泥粘在一起后,小车、C的共同速度为v共,则0=(M+m)v共,得v共=0,故D正确,C错误.
12.【答案】CD
以两物体组成的系统为研究对象,以A的初速度方向为正方向,两个物体的质量均为m,碰撞前系统的总动量:p=7kg m/s+5kg m/s=12kg m/s;
系统的总动能:Ek=。
A.若碰后A、B两球动量为:pA=-2kg m/s,pB=14kg m/s,系统的总动量p′=-2+14=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能增大,是不可能发生的,故A错误;
B.若碰后A、B两球动量为:pA=-4kg m/s,pB=16kg m/s,系统的总动量p′=-4+16=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能增大,是不可能发生的,故B错误;
C.若碰后A、B两球动量为:pA=6kg m/s,pB=6kg m/s,系统的总动量 p′=6+6=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能减小,并且不会发生二次碰撞,是可能发生的,故C正确;
D.若碰后A、B两球动量为:pA=5kg m/s,pB=7kg m/s,系统的总动量 p′=5+7=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能不变,属于弹性碰撞,是可能发生的,故D正确。
故选CD。
13.【答案】(1)C;
(2)AC;
(3)。
(1)为保证两球发生对心正碰,两球的半径应相等,为防止碰撞后入射球反弹,入射球的质量应大于被碰球的质量,故选C;
(2)小球离开轨道后做平抛运动,由得小球做平抛运动的时间,由于小球做平抛运动时抛出点的高度h相同,则它们在空中的运动时间t相等,验证碰撞中的动量守恒,需要验证:m1v1=m1v1′+m2v2,
则:m1v1t=m1v1′t+m2v2t,m1x1=m1x1′+m2x2,由图乙所示可知,需要验证:,
因此实验需要测量的量有:①入射小球的质量,②被碰小球的质量,③入射小球碰前平抛的水平位移,④入射小球碰后平抛的水平位移,⑤被碰小球碰后平抛的水平位移.实验需要刻度尺与天平,故选AC;
(3)若选用甲所示装置,验证碰撞中的动量守恒,需要验证:。
14.【答案】解:(1)木块A与B相碰瞬间,时间很短,B、C之间的摩擦力冲量几乎为零。则C的速度为零,木块A、B的速度相同,则由动量守恒定律得:
解得:;
(2)C滑上A后,摩擦力使C加速、使A减速,直至A、C具有共同速度,以A、C为系统,由动量守恒定律得:
解得:
15.【答案】解:(1)A与B发生弹性碰撞,取水平向右为正方向,根据动量守恒定律和机械能守恒得:
v0=vA+MvB;
由机械能守恒得: v02= vA2+MvB2;
解得vA=-2m/s,vB=4m/s
故B的最大速率为4m/s;
(2)B冲上C并运动到最高点时二者共速设为v,则
MvB=(M+2M)v
可以得到:v=m/s;
(3)从B冲上C然后又滑下的过程,设BC分离时速度分别为vB′、vC′.
由水平动量守恒有
MvB=MvB′+2MvC′
机械能也守恒,有MvB2=MvB′2+ 2MvC′2
联立可以得到:vB′=-m/s
由于|vB′|<|vA|,所有二者不会再次发生碰撞。
答:(1)小球B的最大速率是4m/s;
(2)小球B运动到圆弧曲面最高点时的速率是m/s;
(3)小球B不能与小球A再次发生碰撞。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
一个质量为0.18kg的垒球以20m/s的水平速度向右飞向球棒,被球棒打击后反向水平飞回,速度大小变为40m/s,则这一过程动量的变化量为()
A. 大小10.8kg m/s,方向向右 B. 大小10.8 kg m/s,方向向左
C. 大小3.6 kg m/s,方向向右 D. 大小3.6 kg m/s,方向向左
如图所示,两个质量相等的物体A、B从同一高度沿倾角不同的两固定光滑斜面由静止自由滑下,在到达斜面底端的过程中,下列说法中正确的是( )
A. 两物体所受重力的冲量相同
B. 两物体所受合外力的冲量相同
C. 两物体到达斜面底端时的动量不同
D. 两物体到达斜面底端时的动量水平分量相同
一个质量为0.5 kg的小钢球竖直下落,落地时速度大小为1m/s,与地面作用0.1s后以等大的动量被反弹。小钢球在与地面碰撞的过程中,下列说法中正确的是()
A. 小钢球重力的冲量是0.1 kg·m/s
B. 若选向上为正方向,则小钢球的动量变化量为-1kg·m/s
C. 若选向上为正方向,则小钢球受到的合力冲量是-1 N·s
D. 若小钢球受到的支持力不变,小钢球受到的支持力为15N
如图所示,质量为的半圆轨道小车静止在光滑的水平地面上,其水平直径长度为,现将质量也为的小球从距点正上方高处由静止释放,然后由点经过半圆轨道后从冲出,在空中能上升到距点所在水平线的最大高度为处不计空气阻力,小球可视为质点,则( )
A. 小球和小车组成的系统动量守恒
B. 小球离开小车后做斜向上抛运动
C. 小车向左运动的最大距离为
D. 小球第二次在空中能上升到距点所在水平线的最大高度为
如图所示,一个质量为m1=50 kg的人抓在一只大气球下方,气球下面有一根长绳。气球和长绳的总质量为m2=20 kg,长绳的下端刚好和水平面接触。当静止时人离地面的高度为h=5 m。如果这个人开始沿绳向下滑,当他滑到绳下端时,他离地面高度是(可以把人看作质点) ( )
A. 5 m
B. 3.6 m
C. 2.6 m
D. 8 m
如图所示,质量为的小车和质量为的滑块均静止在光滑水平面上,小车紧靠滑块(不粘连),在小车上固定的轻杆顶端系细绳,绳的末端拴一质量为m的小球,将小球向右拉至细绳水平且绷直后释放,在小球从释放至第一次达到左侧最高点的过程中,下列说法正确的是( )。
A. 小球与小车组成的系统机械能守恒
B. 小球、小车组成的系统在水平方向动量守恒
C. 小球运动至最低点时,小车和滑块分离
D. 小球一定能向左摆到释放时的高度
如图所示,质量为m的A球以速度v0在光滑水平面上运动,与原来静止的质量为4m的B球碰撞,碰撞后A球以v=av0(待定系数a<1)的速率弹回,并与挡板P发生完全弹性碰撞,若要使A球能追上B球再次相撞,则a的取值范围为( )
A. < a< B. < a< C. < a< D. < a≤
如图,两质量分别为和小球在光滑水平面上相向而行,速度大小分别为和,发生碰撞后,系统损失的机械能可能是( )
A. 25 J B. 42 J C. 45 J D. 55 J
如图水平桌面上放置一操作台,操作台上表面水平且光滑。在操作台上放置体积相同,质量不同的甲、乙两球,质量分别为m1、m2,两球用细线相连,中间有一个压缩的轻质弹簧,两球分别与操作台左右边缘距离相等。烧断细线后,由于弹簧弹力的作用,两球分别向左、右运动,脱离弹簧后在操作台面上滑行一段距离,然后平抛落至水平桌面上。则下列说法中正确的是( )
A. 刚脱离弹簧时,甲、乙两球的动量相同
B. 刚脱离弹簧时,甲、乙两球的动能相同
C. 甲、乙两球不会同时落到水平桌面上
D. 甲、乙两球做平抛运动的水平射程之比为m1∶m2
章鱼是一种温带软体动物,生活在水中。一只悬浮在水中的章鱼,当外套膜吸满水后,它的总质量为M,突然发现后方有一只海鳗,章鱼迅速将体内的水通过短漏斗状的体管在极短时间内向后喷出,喷射的水力强劲,从而迅速向前逃窜。若喷射出的水的质量为m,喷射速度为v0,则下列说法正确的是
A. 章鱼喷水的过程中,章鱼和喷出的水组成的系统机械能守恒
B. 章鱼喷水的过程中,章鱼和喷出的水组成的系统动量增加
C. 章鱼喷水后瞬间逃跑的速度大小为
D. 章鱼喷水的过程中受到的冲量为
二、多选题(本大题共2小题,共8.0分)
如图所示,小车放在光滑水平面上,A端固定一个轻弹簧,B端粘有油泥,小车总质量为M,质量为m的木块C放在小车上,用细绳连接于小车的A端并使弹簧压缩,开始时小车和C都静止,当突然烧断细绳时,C被释放,随后离开弹簧向B端冲去,并跟B端油泥粘在一起,忽略一起摩擦,以下说法正确的是( )
A. 弹簧伸长过程中C向右运动,同时小车也向右运动
B. C与B碰前,C与小车的速率之比为M:m
C. C与油泥粘在一起后,小车继续向右运动
D. C与油泥粘在一起后,小车立即停止运动
质量相等的,两球在光滑水平面上沿同一直线、同一方向运动,球的动量是,球的动量是,当球追上球发生碰撞,碰撞后,两球的动量可能值是( )
A. , B. ,
C. , D. ,
三、实验题
在实验室里为了验证动量守恒定律,一般采用如图甲、乙所示的两种装置:
(1)若入射小球质量为m1,半径为r1;被碰小球质量为m2,半径为r2,则________.
A.m1>m2,r1>r2 B.m1>m2,r1
A.直尺
B.游标卡尺
C.天平
D.弹簧测力计
E.秒表
(3)设入射小球的质量为m1,被碰小球的质量为m2,则在用图甲所示装置进行实验时(P为碰前入射小球落点的平均位置),所得“验证动量守恒定律”的结论为______________.(用装置图中的字母表示)
四、计算题
如图所示,在光滑水平面上有两个木块A、B,木块B左端放置小物块C并保持静止,已知,,现木块A以初速度沿水平方向向右滑动,木块A与B相碰后具有共同速度但不粘连,C与A、B间均有摩擦.求:
木块A与B相碰瞬间A木块及小物块C的速度大小;
设木块A足够长,求小物块C的最终速度.
如图所示,光滑水平面上有一质量为2M、半径为R(R足够大)的圆弧曲面C,质量为M的小球B置于其底端,另一个小球A质量为,以v0=6m/s的速度向B运动,并与B发生弹性碰撞,不计一切摩擦,小球均视为质点,求:
(1)小球B的最大速率;
(2)小球B运动到圆弧曲面最高点时的速率;
(3)通过计算判断小球B能否与小球A再次发生碰撞。
答案和解析
1.【答案】B
规定水平向右为正方向,则初动量p1=mv1=0.18kg×20m/s=3.6kg m/s;
打击后动量为:p2=mv2=0.18kg×(-40m/s)=-7.2kg m/s;
故动量变化为:△p=p2-p1=-10.8kg m/s,负号表示方向与规定的正方向相反,即向左;
故选B。
2.【答案】C
解:物体在下滑中只有重力做功,而重力做功只与高度差有关,故两种情况下重力做功相等,由mgh=mv2得两种情况下到达斜面底端的速度的大小是相等的;
A、两种情况下到达斜面底端的速度的大小是相等,又因长的斜面倾角小,物体的加速度小,所以斜面越长下滑的时间越长,所以两种情况下重力作用的时间不相等,重力的冲量也不相等.故A错误;
B、物体在两种情况下到达斜面底端的速度的大小是相等的,而速度的方向不同,所以两种情况下物体的末动量不同.根据动量定理:I=△P=mv-0,所以合力的冲量大小相等,方向是不同的.故B错误;
C、物体在两种情况下到达斜面底端的速度的大小是相等的,方向不同,所以两物体到达斜面底端时的动量不同.故C正确;
D、物体在两种情况下到达斜面底端的速度的大小是相等的,而速度的方向不同,所以两物体到达斜面底端时的动量水平分量不同.故D错误.
故选:C
3.【答案】D
A.根据冲量的定义可知:,故 A错误;
B.若选向上为正方向,则小钢球的动量变化量为,故B错误;
C.根据动量定理,合力冲量等于动量的变化量,所以若选向上为正方向,则小钢球受到的合力冲量是,故 C错误;
D.若选向上为正方向,根据动量定理可得:,解得:,故D正确。
4.【答案】C
A.小球与小车组成的系统在水平方向不受外力,水平方向系统动量守恒,竖直方向小球有加速度,所以系统整体所受合外力不为零,系统动量不守恒,故A错误;
B.小球与小车组成的系统在水平方向动量守恒,小球由B点离开小车时系统水平方向动量为零,小球与小车水平方向速度为零,小球离开小车后做竖直上抛运动,故B错误;
C.设小车向左的最大距离为x,系统水平方向动量守恒,以向右为正方向,在水平方向,由动量守恒定律得:,即,解得,,故C正确;
D.小球第一次车中运动过程中,由动能定理得:,Wf为小球克服摩擦力做功大小,解得:,即小球第一次在车中滚动损失的机械能为:,由于小球第二次在车中滚动时,对应位置处速度变小,因此小车给小球的弹力变小,摩擦力变小,摩擦力做功小于,机械能损失小于,因此小球再次离开小车时,能上升的高度大于:,而小于,故D错误。
5.【答案】B
设人的速度v1,气球的速度v2,根据人和气球动量守恒得
则m1v1=m2v2,
所以v1=v2,
气球和人运动的路程之和为h=5m,则s1=m,s2=m,
即人下滑m,气球上升m,
所以人离地高度为m,约等于3.6m。故B正确,ACD错误。
故选:B。
6.【答案】C
A.对小球、小车和滑块组成的系统,只有重力做功,机械能守恒,因为在整个过程中滑块获得了动能,则小球和小车组成的系统机械能不守恒,故A错误;
B.对小球、小车和滑块组成的系统,在水平方向上不受外力,则在水平方向上动量守恒,小球、小车组成的系统在水平方向动量不守恒,故B错误;
C.小球向左摆到最低点的过程中,速度增大,水平方向上的动量增大,根据动量守恒定律,小车和滑块向右的动量增大,可知向右的速度增大,小球从最低点向左摆时,速度减小,水平方向上的动量减小,则小车向右的动量减小,速度减小,与滑块发生分离,C正确;
D.小球、小车和滑块组成的系统在水平方向上动量守恒,最终滑块的速度不为零,则当小球向左摆到最高点时,水平速度不为零,根据机械能守恒定律知,小球不能摆到释放时的高度,故D错误。
7.【答案】D
A、B碰撞过程中,以v0方向为正方向,根据动量守恒定律得:mv0=-m av0+4mvB
A与挡板P碰撞后能追上B发生再碰的条件是:av0>vB,解得a>
碰撞过程中损失的机械能△E=mv02-[m(av0)2+mvB2]≥0,解得a≤。
所以a满足的条件是<a≤.故ABC错误,D正确。
故选D。
8.【答案】A
当两球发生完全非弹性碰撞时,根据动量守恒有:m1v1-m2v2=(m1+m2)v
解得:v==-4m/s
则损失的最大机械能△E=m1v12+m2v22 (m1+m2)v2=40J
故A正确,BCD错误。
故选A
9.【答案】C
A.取向左为正方向,由动量守恒定律得:p甲+p乙=0,得p甲=-p乙,则刚脱离弹簧时,甲、乙两球的动量大小相等,方向相反,动量不同,故A错误;
B.刚脱离弹簧时,甲、乙两球的动能之比为==,动能不同,故B错误;
C.根据p=mv知,刚脱离弹簧时,甲、乙两球的动量大小相等,质量不同,则刚脱离弹簧时,甲、乙两球的速度大小不等,两球分别与操作台左右边缘距离相等,则两球离开弹簧后在操作台运动的时间不等。两球离开操作台后做平抛运动,两球平抛运动下落的高度相同,则两球平抛运动的时间相同,所以两球不会同时落到水平桌面上,故C正确;
D.甲、乙两球做平抛运动的初速度大小之比v1:v2=||:||=m2:m1,甲、乙两球做平抛运动的水平射程之比为x1:x2=v1t:v2t=m2:m1,故D错误。
故选:C。
10.【答案】C
A、在章鱼喷水的过程中,章鱼的生物能转化为机械能,系统机械能增加,A项错误;
B、章鱼喷水过程所用的时间极短,内力远大于外力,章鱼和喷出的水组成的系统动量守恒,B项错误;
C、由动量守恒定律得0=(M-m)v-,可得章鱼喷水后瞬间逃跑的速度大小为v=,C项正确;
D、章鱼喷水的过程中受到的冲量大小等于喷出的水的动量大小,D项错误。
11.【答案】BD
A.小车与木块C以及弹簧组成的系统在水平方向上动量守恒,C向右运动时,小车应向左运动,故A错误.
B.设碰前C的速率为v1,小车的速率为v2,则0=mv1-Mv2,得=,故B正确.
CD.设C与油泥粘在一起后,小车、C的共同速度为v共,则0=(M+m)v共,得v共=0,故D正确,C错误.
12.【答案】CD
以两物体组成的系统为研究对象,以A的初速度方向为正方向,两个物体的质量均为m,碰撞前系统的总动量:p=7kg m/s+5kg m/s=12kg m/s;
系统的总动能:Ek=。
A.若碰后A、B两球动量为:pA=-2kg m/s,pB=14kg m/s,系统的总动量p′=-2+14=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能增大,是不可能发生的,故A错误;
B.若碰后A、B两球动量为:pA=-4kg m/s,pB=16kg m/s,系统的总动量p′=-4+16=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能增大,是不可能发生的,故B错误;
C.若碰后A、B两球动量为:pA=6kg m/s,pB=6kg m/s,系统的总动量 p′=6+6=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能减小,并且不会发生二次碰撞,是可能发生的,故C正确;
D.若碰后A、B两球动量为:pA=5kg m/s,pB=7kg m/s,系统的总动量 p′=5+7=12kg m/s,遵守动量守恒定律。Ek′=,故碰撞后动能不变,属于弹性碰撞,是可能发生的,故D正确。
故选CD。
13.【答案】(1)C;
(2)AC;
(3)。
(1)为保证两球发生对心正碰,两球的半径应相等,为防止碰撞后入射球反弹,入射球的质量应大于被碰球的质量,故选C;
(2)小球离开轨道后做平抛运动,由得小球做平抛运动的时间,由于小球做平抛运动时抛出点的高度h相同,则它们在空中的运动时间t相等,验证碰撞中的动量守恒,需要验证:m1v1=m1v1′+m2v2,
则:m1v1t=m1v1′t+m2v2t,m1x1=m1x1′+m2x2,由图乙所示可知,需要验证:,
因此实验需要测量的量有:①入射小球的质量,②被碰小球的质量,③入射小球碰前平抛的水平位移,④入射小球碰后平抛的水平位移,⑤被碰小球碰后平抛的水平位移.实验需要刻度尺与天平,故选AC;
(3)若选用甲所示装置,验证碰撞中的动量守恒,需要验证:。
14.【答案】解:(1)木块A与B相碰瞬间,时间很短,B、C之间的摩擦力冲量几乎为零。则C的速度为零,木块A、B的速度相同,则由动量守恒定律得:
解得:;
(2)C滑上A后,摩擦力使C加速、使A减速,直至A、C具有共同速度,以A、C为系统,由动量守恒定律得:
解得:
15.【答案】解:(1)A与B发生弹性碰撞,取水平向右为正方向,根据动量守恒定律和机械能守恒得:
v0=vA+MvB;
由机械能守恒得: v02= vA2+MvB2;
解得vA=-2m/s,vB=4m/s
故B的最大速率为4m/s;
(2)B冲上C并运动到最高点时二者共速设为v,则
MvB=(M+2M)v
可以得到:v=m/s;
(3)从B冲上C然后又滑下的过程,设BC分离时速度分别为vB′、vC′.
由水平动量守恒有
MvB=MvB′+2MvC′
机械能也守恒,有MvB2=MvB′2+ 2MvC′2
联立可以得到:vB′=-m/s
由于|vB′|<|vA|,所有二者不会再次发生碰撞。
答:(1)小球B的最大速率是4m/s;
(2)小球B运动到圆弧曲面最高点时的速率是m/s;
(3)小球B不能与小球A再次发生碰撞。
第2页,共2页
第1页,共1页
