9.1.1 不等式及其解集 课件(共27张PPT)
文档属性
| 名称 | 9.1.1 不等式及其解集 课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 08:27:57 | ||
图片预览







文档简介
(共27张PPT)
第九章 不等式与不等式组
9.1 不等式
9.1.1 不等式及其解集
人教版数学七年级下册 同步课件
1.了解不等式及其解的概念;
2.学会并准确运用不等式表示数量关系,形成在表
达中渗透数形结合的思想;(难点)
3.理解不等式的解集及解不等式的意义.(重点)
学习目标
谁长谁短
谁快谁慢
谁重谁轻
谁赢谁输
新课导入
新课导入
现实生活中, 数量之间存在着相等与不相等的关系.
例如, 小明的身高为155cm, 小美的身高为156cm.
则我们可以用不等号 “>” 或 “<” 来表示他们的身高之间
的关系.
如: 156 > 155或155 < 156.
155cm
156cm
不等式的概念
问题1 如图所示,处于平衡状态的托盘天平的右盘放上一质量为50g的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量x g与质量为50g的砝码之间具有怎样的关系?
我们很容易知道圆球的质量大于砝码的质量,即x > 50.
探究新知
一辆匀速行驶的汽车在11:20距离A地50km, 要12:00之前驶过A地, 车速应满足什么条件?
A
50km
11:20
12:00
40min= h
若设车速为 x km/h, 你能用一个式子表示吗?
x >50.
从路程看
以这个速度行驶 h的路程要超过50km.
从时间看
以这个速度行驶50km所用的时间不到 h.
.
探究新知
思考: 下列式子有什么区别?
区别:
①只有(4)的式子里含有 “=” 符号;
②除了(4)的式子里都含有 “>” 或 “<” 或 “≥” 或 “≤” 或 “≠” 符号.
我们把像156>155, 155<156, x>50 这样, 用符号 “>” 或 “<”连接而成的式子叫做不等式. 像a≠2这样的式子也叫做不等式.
探究新知
判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4)x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式;
(3)(4)不是不等式.
针对练习
用不等式表示数量关系
例1 用不等式表示下列数量关系:
(1)x的5倍大于-7;
(2)a与b的和的一半小于-1;
(3)长、宽分别为xcm,ycm的长方形的面积小于
边长为acm的正方形的面积.
5x >-7
xy < a2
探究新知
例2 已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解 3x+10(x+y)<50
探究新知
交流: 下面给出的数中, 能使不等式 x>50成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
当x=20, 20<50, 不成立;
当x=40, 40<50, 不成立;
当x=50, 50=50, 不成立;
当x=100, 100>50, 成立.
解:
代入法是检验某个值是否是不等式的解的简单、实用的方法.
探究新知
不等式的解与解集
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解.
例如:100是x>50的解.
概念学习
判断下列数中哪些是不等式 的解:60,73,74.9,75.1,76,79,80,90.你还能找出这个不等式的其他解吗?这个不等式有多少个解?
(2)你从表格中发现了什么规律?
(1)你发现了哪些数是这个不等式的解?
xx 60 73 74.9 75.1 76 79 80 90
不
是
是
是
不是
不是
是
是
是
无数个
探究新知
解含有未知数的不等式的所有解组成这个不等式的解集.
求不等式解集的过程叫做解不等式.
探究新知
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
问题1 如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
在数轴上表示不等式的解集
探究新知
解集的表示方法:
第一种:用式子(如x>2),即用最简形式的不等式
(如x>a或x第二种:用数轴,一般标出数轴上某一区间,其中的
点对应的数值都是不等式的解.
用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 ; (2) x< .
0
-1
0
1
变式:
已知x的解集在数轴上表示如图,你能写出x的
解集吗
0
-2
x<-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
用数轴表示不等式的解集,应记住下面的规律:
1.大于向右画,小于向左画;
2.>,<画空心圆圈.
总结归纳
例3 直接写出x+4<6的解集,并在数轴上表示出来.
0
1
2
解:x<2.
这个解集可以在数轴上表示为:
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
变式1:已知x的解集如图所示,你能写出x的解集吗
1.下列式子中,不成立的是( )
A.-2>-1 B.3>2
C.0>-1 D.2>-1
2.在式子-3<0,x≥2,x=a,x2-2x,x≠3,x+1>y中,是不等式的有( )
A.2个 B.3个 C.4个 D.5个
3.某市最高气温是33 ℃,最低气温是24 ℃,则该市气温t(℃)的变化范围是( )
A.t>33 ℃ B.t≤24 ℃
C.24 ℃A
C
D
课堂练习
C
-36.如果a>b,那么下列不等式中一定成立的是( )
A.a2>b2 B.1-a>1-b
C.1+a>1-b D.1+a>b-1
7.下列不等式中,不含有x=-1这个解的是( )
A.2x+1≤-3 B.2x-1≥-3
C.-2x+1≥3 D.-2x-1≤3
8.如果不等式(a+1)x1,那么a的取值范围是____________.
D
A
a<-1
课堂小结
不等式及其解集
我们把用符号 “>” 或 “<” 连接而成的式子叫做不等式. 像a≠2这样的式子也叫做不等.
能使不等式成立的未知数的值叫不等式的解.
解含有未知数的不等式的所有解组成这个不等式的解集.
求不等式解集的过程叫做解不等式.
解集表示方式: ①不等式; ②数轴.
https://www.21cnjy.com/help/help_extract.php
第九章 不等式与不等式组
9.1 不等式
9.1.1 不等式及其解集
人教版数学七年级下册 同步课件
1.了解不等式及其解的概念;
2.学会并准确运用不等式表示数量关系,形成在表
达中渗透数形结合的思想;(难点)
3.理解不等式的解集及解不等式的意义.(重点)
学习目标
谁长谁短
谁快谁慢
谁重谁轻
谁赢谁输
新课导入
新课导入
现实生活中, 数量之间存在着相等与不相等的关系.
例如, 小明的身高为155cm, 小美的身高为156cm.
则我们可以用不等号 “>” 或 “<” 来表示他们的身高之间
的关系.
如: 156 > 155或155 < 156.
155cm
156cm
不等式的概念
问题1 如图所示,处于平衡状态的托盘天平的右盘放上一质量为50g的砝码,左盘放上一个圆球后向左倾斜,问圆球的质量x g与质量为50g的砝码之间具有怎样的关系?
我们很容易知道圆球的质量大于砝码的质量,即x > 50.
探究新知
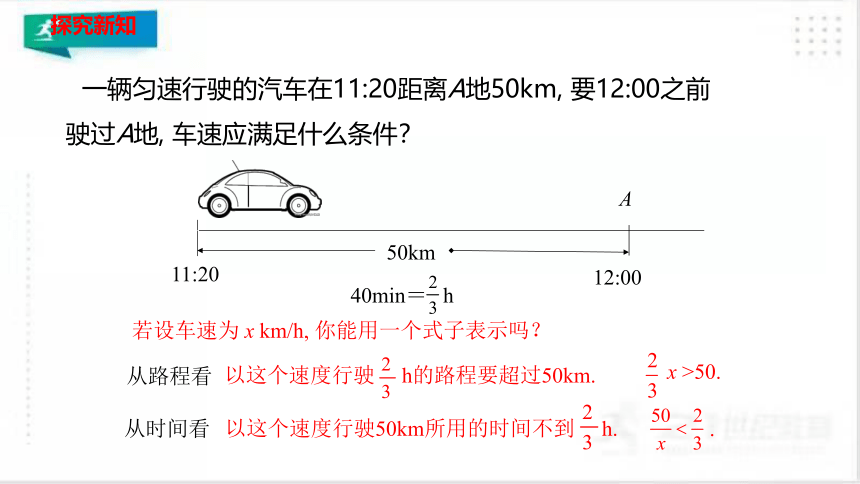
一辆匀速行驶的汽车在11:20距离A地50km, 要12:00之前驶过A地, 车速应满足什么条件?
A
50km
11:20
12:00
40min= h
若设车速为 x km/h, 你能用一个式子表示吗?
x >50.
从路程看
以这个速度行驶 h的路程要超过50km.
从时间看
以这个速度行驶50km所用的时间不到 h.
.
探究新知
思考: 下列式子有什么区别?
区别:
①只有(4)的式子里含有 “=” 符号;
②除了(4)的式子里都含有 “>” 或 “<” 或 “≥” 或 “≤” 或 “≠” 符号.
我们把像156>155, 155<156, x>50 这样, 用符号 “>” 或 “<”连接而成的式子叫做不等式. 像a≠2这样的式子也叫做不等式.
探究新知
判断下列式子是不是不等式:
(1)-3>0; (2)4x+3y<0;
(3)x=3; (4)x2+xy+y2;
(5)x≠5; (6)x+2>y+5.
解 : (1)(2)(5)(6)是不等式;
(3)(4)不是不等式.
针对练习
用不等式表示数量关系
例1 用不等式表示下列数量关系:
(1)x的5倍大于-7;
(2)a与b的和的一半小于-1;
(3)长、宽分别为xcm,ycm的长方形的面积小于
边长为acm的正方形的面积.
5x >-7
xy < a2
探究新知
例2 已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解 3x+10(x+y)<50
探究新知
交流: 下面给出的数中, 能使不等式 x>50成立吗?你还能找出其他的数吗?
20, 40, 50, 100.
当x=20, 20<50, 不成立;
当x=40, 40<50, 不成立;
当x=50, 50=50, 不成立;
当x=100, 100>50, 成立.
解:
代入法是检验某个值是否是不等式的解的简单、实用的方法.
探究新知
不等式的解与解集
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解.
例如:100是x>50的解.
概念学习
判断下列数中哪些是不等式 的解:60,73,74.9,75.1,76,79,80,90.你还能找出这个不等式的其他解吗?这个不等式有多少个解?
(2)你从表格中发现了什么规律?
(1)你发现了哪些数是这个不等式的解?
xx 60 73 74.9 75.1 76 79 80 90
不
是
是
是
不是
不是
是
是
是
无数个
探究新知
解含有未知数的不等式的所有解组成这个不等式的解集.
求不等式解集的过程叫做解不等式.
探究新知
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
问题1 如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2 的点A 画成空心圆圈,表示解集不包括2.
在数轴上表示不等式的解集
探究新知
解集的表示方法:
第一种:用式子(如x>2),即用最简形式的不等式
(如x>a或x
点对应的数值都是不等式的解.
用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 ; (2) x< .
0
-1
0
1
变式:
已知x的解集在数轴上表示如图,你能写出x的
解集吗
0
-2
x<-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
用数轴表示不等式的解集,应记住下面的规律:
1.大于向右画,小于向左画;
2.>,<画空心圆圈.
总结归纳
例3 直接写出x+4<6的解集,并在数轴上表示出来.
0
1
2
解:x<2.
这个解集可以在数轴上表示为:
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
变式1:已知x的解集如图所示,你能写出x的解集吗
1.下列式子中,不成立的是( )
A.-2>-1 B.3>2
C.0>-1 D.2>-1
2.在式子-3<0,x≥2,x=a,x2-2x,x≠3,x+1>y中,是不等式的有( )
A.2个 B.3个 C.4个 D.5个
3.某市最高气温是33 ℃,最低气温是24 ℃,则该市气温t(℃)的变化范围是( )
A.t>33 ℃ B.t≤24 ℃
C.24 ℃
C
D
课堂练习
C
-3
A.a2>b2 B.1-a>1-b
C.1+a>1-b D.1+a>b-1
7.下列不等式中,不含有x=-1这个解的是( )
A.2x+1≤-3 B.2x-1≥-3
C.-2x+1≥3 D.-2x-1≤3
8.如果不等式(a+1)x
D
A
a<-1
课堂小结
不等式及其解集
我们把用符号 “>” 或 “<” 连接而成的式子叫做不等式. 像a≠2这样的式子也叫做不等.
能使不等式成立的未知数的值叫不等式的解.
解含有未知数的不等式的所有解组成这个不等式的解集.
求不等式解集的过程叫做解不等式.
解集表示方式: ①不等式; ②数轴.
https://www.21cnjy.com/help/help_extract.php
