4.2万有引力定律的应用 同步练习(Word版含解析)
文档属性
| 名称 | 4.2万有引力定律的应用 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-01 04:43:00 | ||
图片预览




文档简介
鲁科版 (2019)必修第二册 4.2 万有引力定律的应用 同步练习
一、单选题
1.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原地。若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。已知该星球的半径与地球半径之比为R星∶R地=1∶4,地球表面重力加速度为g,设该星球表面附近的重力加速度为g′,空气阻力不计。则( )
A.g′∶g=1∶5 B.g′∶g=5∶2
C.M星∶M地=1∶20 D.M星∶M地=80∶1
2.2020年12月1日,嫦娥五号探测器着陆月球,持续约2天的月面工作,采集2千克左右的月球样品。嫦娥五号探测器在着陆之前先贴近月球表面做匀速圆周运动,测得探测器绕月运行周期为。已知引力常量为,由以上数据能求出的物理量是( )
A.地球的质量 B.月球的质量
C.月球表面的重力加速度 D.月球的密度
3.百余年前,爱因斯坦广义相对论率先对黑洞作出预言。时至今日,全球多地天文学家同步公布了人类首张黑洞照片。若某小型黑洞的半径R约45km,质量M和半径R的关系满足(其中c为真空中的光速,G为引力常量),则该黑洞表面重力加速度的数量级为( )
A. B. C. D.
4.一火箭以a=的加速度竖直升空。为了监测火箭到达的高度,可以观察火箭上搭载物视重的变化。如果火箭上搭载的一物体的质量为m=1.6kg,当检测仪器显示物体的视重为F=9N时,火箭距离地面的高度h与地球半径R的关系为(取g=10m/s2)( )
A.h=R B.h=2R C.h=3R D.h=4R
5.已知万有引力常量,地球中心到球的距离约为地球半径的60倍,你也可以利用自己掌握的万有引力的知识估算地球的平均密度。当然你也可以利用自己掌握的其它知识估算地球的平均密度。通过估算可得地球的平均密度最接近下列哪个值( )
A.5×102kg/m3 B.6×103kg/m3 C.5×104kg/m3 D.6×105kg/m3
6.在半径为 R1的 K 星球表面竖直向上提起一质量为 m1的物体,拉力 F 与物体加速度 a 的关系如图线 1 所示。在半径为 R2的 T 星球表面竖直向上提起一质量为 m2的物体,拉力 F 与物体加速度 a 的关系如图线 2 所示。设两星球密度相等,质量分布均匀。则 ( )
A.m1 : m2=3 : 1,R1 : R2=1 : 2 B.m1 : m2=3 : 2,R1 : R2=3 : 1
C.m1 : m2=3 : 1,R1 : R2=2 : 3 D.m1 : m2=3 : 2,R1 : R2=2 : 1
7.2021年5月22日10时40分,随着火星探测器“祝融”号的成功登陆,我国成为世界上第二个登陆火星的国家。祝融号质量约,高,设计寿命约92天,静置时其在火星对火星表面的压力约。下列相关说法正确的是( )
A.、、是国际单位制中的基本单位
B.“2021年5月22日10时40分”指的是时间
C.祝融号对火星的压力与火星对祝融号的支持力是一对平衡力
D.祝融号在火星上受到火星的引力比其在地球上受到的地球引力小
8.宇航员在月球上将一小石块水平抛出,最后落在月球表面上,如果已知月球半径为R、引力常量为G。要估算月球质量,还需测量出小石块运动的物理量是( )
A.抛出的高度h和水平位移x
B.抛出的高度h和运动时间t
C.水平位移x和运动时间t
D.抛出的高度h和抛出点到落地点的距离L
9.假设某探测器在着陆火星前贴近火星表面运行一周用时为T,已知火星的半径为R1,地球的半径为R2,地球的质量为M,地球表面的重力加速度为g,引力常量为G,则火星的质量为( )
A. B.
C. D.
10.月球绕地球公转做匀速圆周运动的向心加速度大小为a,在月球绕地球运行的轨道处由地球引力产生的加速度大小为g1,月球表面的重力加速度为g2,(月球距离地球较远,分析月球表面重力加速度时可不考虑地球引力影响),以下关系正确的是( )
A. B. C. D.
11.已知某半径为r0的质量分布均匀的天体,测得它的一个卫星的圆轨道的半径为r,卫星运行的周期为T。假设在该天体表面沿竖直方向以初速度v0向上抛出一个物体,不计阻力,求它可以到达的最大高度h是( )
A. B. C. D.
12.有A、B两颗绕地球运动的人造卫星,其轨道分别为如图所示的Ⅰ和Ⅱ,轨道Ⅰ为半径为R的圆。轨道Ⅱ为长轴等于的椭圆,O点为地球球心位置,已知地球质量为M,万有引力常量为G。下列说法正确的是( )
A.B从c经b到d的过程,速率先增大再减小
B.若A的运行速率为,设B经过b点时的速率为v1,则
C.若,则B经过b点时的加速度与A的加速度之比为9∶4
D.A、B运行周期之比
13.火星探测器着陆火星时,就可以用下面方法测量的火星的半径:先让飞船在火星引力的作用下在火星表面附近绕火星做匀速圆周运动,记下环绕一周所用的时间T,然后回到火星表面,从高h处自由落下一个小球,记录小球下落的时间t,由此可测得火星的半径为( )
A. B. C. D.
14.2021年10月16日神舟十三号载人飞船顺利发射升空,翟志刚、王亚平、叶光富3名航天员开启了为期6个月的天宫空间站之旅。神舟十三号飞船在经历上升、入轨交会飞行后,与空间站天和核心舱对接,组合体在距离地球表面400公里的轨道运行。下列说法正确的是( )
A.组合体的周期大于24小时
B.组合体的线速度小于第一宇宙速度
C.组合体的角速度小于同步卫星的角速度
D.神舟十三号加速上升阶段,航天员有失重感觉
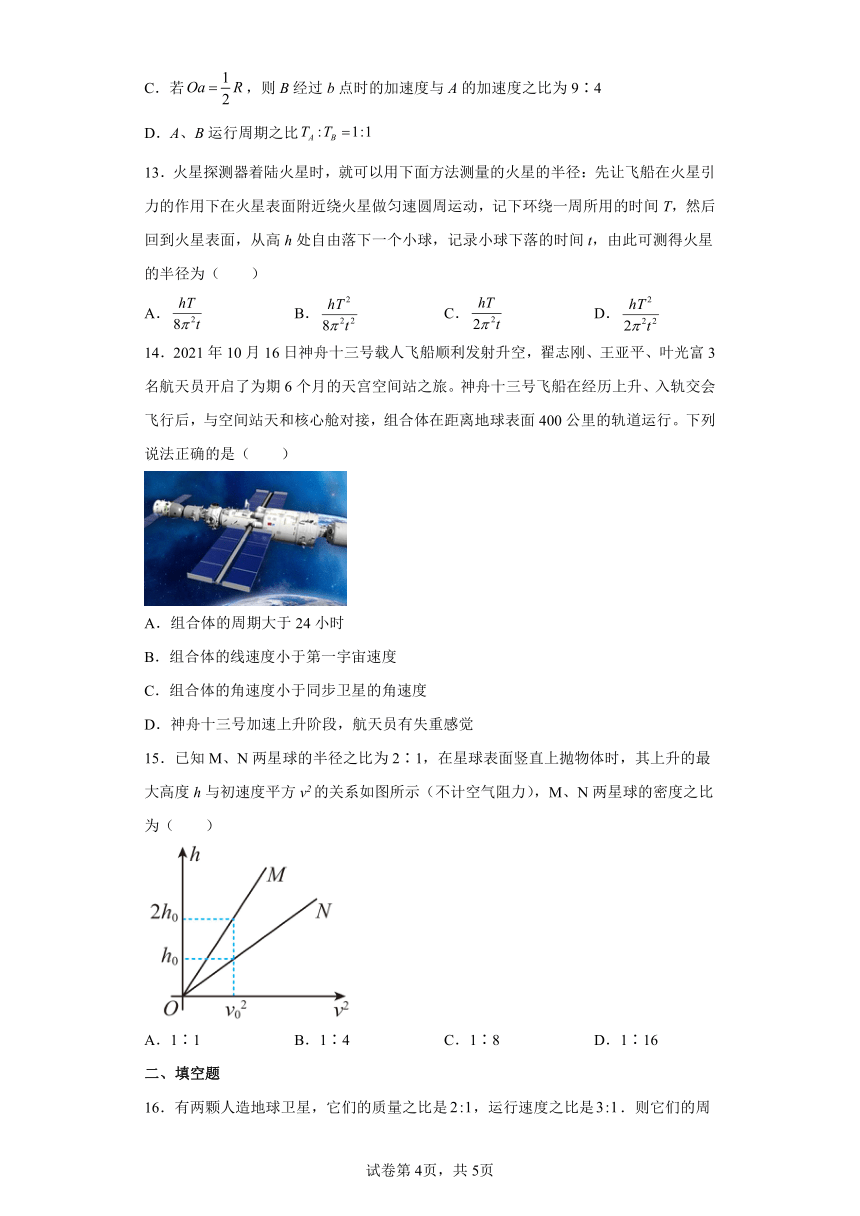
15.已知M、N两星球的半径之比为2∶1,在星球表面竖直上抛物体时,其上升的最大高度h与初速度平方v2的关系如图所示(不计空气阻力),M、N两星球的密度之比为( )
A.1∶1 B.1∶4 C.1∶8 D.1∶16
二、填空题
16.有两颗人造地球卫星,它们的质量之比是,运行速度之比是.则它们的周期之比________;轨道半径之比________;所受向心力之比________.
17.当在地球表面物体的重力等于引力时,可推导“黄金代换”公式:______________;
18.已知引力常量,重力加速度g=9.8m/s2,地球半径为R=6.4×106m,则可知地球质量为________kg.
三、解答题
19.某人造地球卫星沿圆轨道运行,轨道半径是,周期是s。试从这些数据估算地球的质量。
20.地球赤道上的物体,由于地球自转产生的向心加速度,赤道上的重力加速度,试问:质量为的物体在地球赤道上所受地球的万有引力为多大?
21.如图所示,一个质量为M的匀质实心球,半径为R。如果通过球心挖去一个直径为R的小实心球,然后置于相距为d的地方,试计算空心球与小实心球之间的万有引力。
22.如果你站在月球上,能否用一把刻度尺和一块秒表估测月球的质量?如果能,请设计实验,并说出需要测量的数据和月球质量的计算式。已知月球的半径为R。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
AB.由速度对称性知竖直上抛的小球在空中运动时间
因此得
A正确;B错误;
CD.由
得
因而
CD错误;
故选A。
2.D
【解析】
【详解】
A.题干给出的是嫦娥五号绕月运动的相关信息,无法求得地球的质量,故A不符合题意;
BCD.设月球和探测器的质量分别为M、m,月球的半径为R,月球表面的重力加速度为g,由题意,根据牛顿第二定律有
月球的体积为
月球的密度为
联立以上三式解得
由于R未知,所以M和g均无法求出,故BC不符合题意,D符合题意。
故选D。
3.C
【解析】
【分析】
【详解】
由
可知黑洞表面的加速度
故选C。
4.C
【解析】
【详解】
设火箭距离地面的高度为h,该处的重力加速度为g′,地球的半径为R。根据牛顿第二定律,有
F-mg′=ma
即
g′==0.625m/s2
根据万有引力定律,有
所以
即
所以火箭距离地面的高度h=3R,故ABD错误,C选项正确。
故选:C。
5.B
【解析】
【分析】
【详解】
设质量为m的物体放在地球的表面,地球的质量为M,根据物体的重力等于地球对物体的万有引力
地球的半径 ,地球表面的重力加速度为 ,则
地球的体积
根据
故选B。
6.A
【解析】
【详解】
物体在星球表面竖直向上加速,根据牛顿第二定律有
变形得
则图线的斜率表示物体的质量,则有
,
故
当时,拉力等于物体的重力,则有
、
则重力加速度之比为
根据物体在星球表面上,万有引力等于重力,则有
又
联立解得
故
故选A。
7.D
【解析】
【详解】
A.、是国际单位制中的基本单位,是导出单位,故A错误;
B.“2021年5月22日10时40分”指的是一个瞬间,为时刻,故B错误;
C.祝融号对火星的压力与火星对祝融号的支持力是一对作用力与反作用力,故C错误;
D.祝融号质量约,由于它在地球表面上受到的万有引力大小近似等于重力,可知约为;根据祝融号在火星表面静置时其对火星表面的压力约,可知它在火星表面上受到的重力约等于,也即祝融号在火星上受到火星的引力约为,所以祝融号在火星上受到火星的引力比其在地球上受到的地球引力小,故D正确。
故选D。
8.B
【解析】
【详解】
由
G=mg
得
M=
对平抛运动,水平位移
x=v0t
竖直位移
h=gt2
得
g=
因此得
M=
或
M=
要估算月球质量,还需测量出小石块运动的物理量是抛出的高度h和运动时间t,或者测出抛出的高度h和水平位移x以及初速度v0;
故选B。
9.A
【解析】
【详解】
绕地球表面运动的物体,由牛顿第二定律可知
绕火星表面运动的探测器
解得
故选A。
10.B
【解析】
【详解】
月球绕地球公转做匀速圆周运动,它的向心力由地球引起的,所以在月球绕地球运行的轨道处由地球引力产生的加速度大小就等于月球绕地球做匀速圆周运动的向心力加速度大小,即
根据万有引力等于重力得,在月球表面处由月球引力产生的加速度大小等于月球表面的加速度大小,所以g1、g2、a之间无直接关系。
故选B。
11.D
【解析】
【详解】
由万有引力提供向心力得
①
在天体表面有
②
在该天体表面沿竖直方向以初速度v0向上抛出一个物体,不计阻力,物体上升的过程中的机械能守恒,由机械能守恒定律有
③
由①②③式可知,物体可以到达的最大高度
故选D。
12.D
【解析】
【详解】
A.根据开普勒第二定律可知,B从c经b到d的过程中,速率先减小后增大,故A错误;
B.设地球的质量为M,卫星的质量为m,卫星在半径为r的圆轨道做匀速圆周运动时的速率为v,则根据牛顿第二定律有
解得
设卫星在以Ob为半径的圆轨道上做匀速圆周运动的速率为v2,则由上式可知
根据卫星的变轨特点可知
所以
故B错误;
C.根据牛顿第二定律可知B经过b点时的加速度与A的加速度之比为
故C错误;
D.根据开普勒第三定律可知
故D正确。
故选D。
13.D
【解析】
【详解】
因为飞船在火星表面附近绕火星做匀速圆周运动时,满足
又在天体表面满足
又由自由落体运动规律得
联立解得
故选D。
14.B
【解析】
【详解】
ABC.设地球质量为M,质量为m的物体绕地球做轨道半径为r、周期为T、角速度为ω、线速度为v的匀速圆周运动,根据牛顿第二定律有
分别解得
①
②
③
由于地球同步卫星的轨道高度约为36000km,远大于组合体的轨道高度,根据③式可知组合体的周期小于24小时;根据②式可知组合体的角速度大于同步卫星的角速度;第一宇宙速度是物体在地球表面附近绕地球做匀速圆周运动的速度,而组合体轨道半径大于地球半径,根据①式可知组合体的线速度小于第一宇宙速度,故AC错误,B正确;
D.神舟十三号加速上升阶段,航天员的加速度方向向上,有超重感觉,故D错误。
故选B。
15.B
【解析】
【详解】
由竖直上抛运动和题图可知
,
所以
根据
, ,
得
所以
故选B。
16.
【解析】
【详解】
卫星做圆周运动万有引力提供向心力:,解得:,轨道半径之比;根据万有引力提供向心力:,解得:,它们的周期之比;万有引力为,所受向心力之比.
17.
【解析】
【详解】
根据 ,可得 ,从而知道黄金代换公式.
18.
【解析】
【详解】
物体在地球表面,当忽略自转作用时,所受的万有引力即为重力,有,可得.
【点睛】
掌握求中心天体的质量的两类方法;一是用,二是用环绕天体的转动;解决本题的关键掌握万有引力等于重力这一理论,并能灵活运用.
19.
【解析】
【详解】
设某人造地球卫星质量为m,地球质量为M,沿圆轨道运行时由万有引力提供向心力可得
解得
代入数据解得
20.
【解析】
【分析】
【详解】
在赤道上,万有引力一部分分解为重力,另一部分提供向心力,则有
21.
【解析】
【分析】
实心球挖去一个半径为的小实心球后,质量分布不均匀。因此挖去小实心球剩余的部分,不能看成质量集中于球心的质点,直接求空心球和小实心球之间的万有引力很困难。
【详解】
假设用与挖去的小实心球完全相同的球填补挖去的位置,则空心球变成一个实心球,可看作质量集中于球心的质点,则大、小实心球之间的万有引力为
F=G
小实心球的质量为
m=ρ·π=ρ·πR3=M
代入上式得
F=G
填入的小实心球与挖去的小实心球之间的万有引力为
F1=G=·=
设空心球与小实心球之间的万有引力为F2,则有F=F1+F2因此,空心球与小实心球之间的万有引力为
F2=F-F1=-
22.能,下落的高度和所需时间,
【解析】
【详解】
能估计测出月球的质量
在月球表面用让一重物做自由落体运动,用刻度尺测出下落的高度h,用秒表测量出下落的时间t,根据
求得月球表面的重力加速度,即
根据万有引力等于重力得
月球的质量
答案第1页,共2页
答案第1页,共2页
一、单选题
1.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原地。若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。已知该星球的半径与地球半径之比为R星∶R地=1∶4,地球表面重力加速度为g,设该星球表面附近的重力加速度为g′,空气阻力不计。则( )
A.g′∶g=1∶5 B.g′∶g=5∶2
C.M星∶M地=1∶20 D.M星∶M地=80∶1
2.2020年12月1日,嫦娥五号探测器着陆月球,持续约2天的月面工作,采集2千克左右的月球样品。嫦娥五号探测器在着陆之前先贴近月球表面做匀速圆周运动,测得探测器绕月运行周期为。已知引力常量为,由以上数据能求出的物理量是( )
A.地球的质量 B.月球的质量
C.月球表面的重力加速度 D.月球的密度
3.百余年前,爱因斯坦广义相对论率先对黑洞作出预言。时至今日,全球多地天文学家同步公布了人类首张黑洞照片。若某小型黑洞的半径R约45km,质量M和半径R的关系满足(其中c为真空中的光速,G为引力常量),则该黑洞表面重力加速度的数量级为( )
A. B. C. D.
4.一火箭以a=的加速度竖直升空。为了监测火箭到达的高度,可以观察火箭上搭载物视重的变化。如果火箭上搭载的一物体的质量为m=1.6kg,当检测仪器显示物体的视重为F=9N时,火箭距离地面的高度h与地球半径R的关系为(取g=10m/s2)( )
A.h=R B.h=2R C.h=3R D.h=4R
5.已知万有引力常量,地球中心到球的距离约为地球半径的60倍,你也可以利用自己掌握的万有引力的知识估算地球的平均密度。当然你也可以利用自己掌握的其它知识估算地球的平均密度。通过估算可得地球的平均密度最接近下列哪个值( )
A.5×102kg/m3 B.6×103kg/m3 C.5×104kg/m3 D.6×105kg/m3
6.在半径为 R1的 K 星球表面竖直向上提起一质量为 m1的物体,拉力 F 与物体加速度 a 的关系如图线 1 所示。在半径为 R2的 T 星球表面竖直向上提起一质量为 m2的物体,拉力 F 与物体加速度 a 的关系如图线 2 所示。设两星球密度相等,质量分布均匀。则 ( )
A.m1 : m2=3 : 1,R1 : R2=1 : 2 B.m1 : m2=3 : 2,R1 : R2=3 : 1
C.m1 : m2=3 : 1,R1 : R2=2 : 3 D.m1 : m2=3 : 2,R1 : R2=2 : 1
7.2021年5月22日10时40分,随着火星探测器“祝融”号的成功登陆,我国成为世界上第二个登陆火星的国家。祝融号质量约,高,设计寿命约92天,静置时其在火星对火星表面的压力约。下列相关说法正确的是( )
A.、、是国际单位制中的基本单位
B.“2021年5月22日10时40分”指的是时间
C.祝融号对火星的压力与火星对祝融号的支持力是一对平衡力
D.祝融号在火星上受到火星的引力比其在地球上受到的地球引力小
8.宇航员在月球上将一小石块水平抛出,最后落在月球表面上,如果已知月球半径为R、引力常量为G。要估算月球质量,还需测量出小石块运动的物理量是( )
A.抛出的高度h和水平位移x
B.抛出的高度h和运动时间t
C.水平位移x和运动时间t
D.抛出的高度h和抛出点到落地点的距离L
9.假设某探测器在着陆火星前贴近火星表面运行一周用时为T,已知火星的半径为R1,地球的半径为R2,地球的质量为M,地球表面的重力加速度为g,引力常量为G,则火星的质量为( )
A. B.
C. D.
10.月球绕地球公转做匀速圆周运动的向心加速度大小为a,在月球绕地球运行的轨道处由地球引力产生的加速度大小为g1,月球表面的重力加速度为g2,(月球距离地球较远,分析月球表面重力加速度时可不考虑地球引力影响),以下关系正确的是( )
A. B. C. D.
11.已知某半径为r0的质量分布均匀的天体,测得它的一个卫星的圆轨道的半径为r,卫星运行的周期为T。假设在该天体表面沿竖直方向以初速度v0向上抛出一个物体,不计阻力,求它可以到达的最大高度h是( )
A. B. C. D.
12.有A、B两颗绕地球运动的人造卫星,其轨道分别为如图所示的Ⅰ和Ⅱ,轨道Ⅰ为半径为R的圆。轨道Ⅱ为长轴等于的椭圆,O点为地球球心位置,已知地球质量为M,万有引力常量为G。下列说法正确的是( )
A.B从c经b到d的过程,速率先增大再减小
B.若A的运行速率为,设B经过b点时的速率为v1,则
C.若,则B经过b点时的加速度与A的加速度之比为9∶4
D.A、B运行周期之比
13.火星探测器着陆火星时,就可以用下面方法测量的火星的半径:先让飞船在火星引力的作用下在火星表面附近绕火星做匀速圆周运动,记下环绕一周所用的时间T,然后回到火星表面,从高h处自由落下一个小球,记录小球下落的时间t,由此可测得火星的半径为( )
A. B. C. D.
14.2021年10月16日神舟十三号载人飞船顺利发射升空,翟志刚、王亚平、叶光富3名航天员开启了为期6个月的天宫空间站之旅。神舟十三号飞船在经历上升、入轨交会飞行后,与空间站天和核心舱对接,组合体在距离地球表面400公里的轨道运行。下列说法正确的是( )
A.组合体的周期大于24小时
B.组合体的线速度小于第一宇宙速度
C.组合体的角速度小于同步卫星的角速度
D.神舟十三号加速上升阶段,航天员有失重感觉
15.已知M、N两星球的半径之比为2∶1,在星球表面竖直上抛物体时,其上升的最大高度h与初速度平方v2的关系如图所示(不计空气阻力),M、N两星球的密度之比为( )
A.1∶1 B.1∶4 C.1∶8 D.1∶16
二、填空题
16.有两颗人造地球卫星,它们的质量之比是,运行速度之比是.则它们的周期之比________;轨道半径之比________;所受向心力之比________.
17.当在地球表面物体的重力等于引力时,可推导“黄金代换”公式:______________;
18.已知引力常量,重力加速度g=9.8m/s2,地球半径为R=6.4×106m,则可知地球质量为________kg.
三、解答题
19.某人造地球卫星沿圆轨道运行,轨道半径是,周期是s。试从这些数据估算地球的质量。
20.地球赤道上的物体,由于地球自转产生的向心加速度,赤道上的重力加速度,试问:质量为的物体在地球赤道上所受地球的万有引力为多大?
21.如图所示,一个质量为M的匀质实心球,半径为R。如果通过球心挖去一个直径为R的小实心球,然后置于相距为d的地方,试计算空心球与小实心球之间的万有引力。
22.如果你站在月球上,能否用一把刻度尺和一块秒表估测月球的质量?如果能,请设计实验,并说出需要测量的数据和月球质量的计算式。已知月球的半径为R。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
AB.由速度对称性知竖直上抛的小球在空中运动时间
因此得
A正确;B错误;
CD.由
得
因而
CD错误;
故选A。
2.D
【解析】
【详解】
A.题干给出的是嫦娥五号绕月运动的相关信息,无法求得地球的质量,故A不符合题意;
BCD.设月球和探测器的质量分别为M、m,月球的半径为R,月球表面的重力加速度为g,由题意,根据牛顿第二定律有
月球的体积为
月球的密度为
联立以上三式解得
由于R未知,所以M和g均无法求出,故BC不符合题意,D符合题意。
故选D。
3.C
【解析】
【分析】
【详解】
由
可知黑洞表面的加速度
故选C。
4.C
【解析】
【详解】
设火箭距离地面的高度为h,该处的重力加速度为g′,地球的半径为R。根据牛顿第二定律,有
F-mg′=ma
即
g′==0.625m/s2
根据万有引力定律,有
所以
即
所以火箭距离地面的高度h=3R,故ABD错误,C选项正确。
故选:C。
5.B
【解析】
【分析】
【详解】
设质量为m的物体放在地球的表面,地球的质量为M,根据物体的重力等于地球对物体的万有引力
地球的半径 ,地球表面的重力加速度为 ,则
地球的体积
根据
故选B。
6.A
【解析】
【详解】
物体在星球表面竖直向上加速,根据牛顿第二定律有
变形得
则图线的斜率表示物体的质量,则有
,
故
当时,拉力等于物体的重力,则有
、
则重力加速度之比为
根据物体在星球表面上,万有引力等于重力,则有
又
联立解得
故
故选A。
7.D
【解析】
【详解】
A.、是国际单位制中的基本单位,是导出单位,故A错误;
B.“2021年5月22日10时40分”指的是一个瞬间,为时刻,故B错误;
C.祝融号对火星的压力与火星对祝融号的支持力是一对作用力与反作用力,故C错误;
D.祝融号质量约,由于它在地球表面上受到的万有引力大小近似等于重力,可知约为;根据祝融号在火星表面静置时其对火星表面的压力约,可知它在火星表面上受到的重力约等于,也即祝融号在火星上受到火星的引力约为,所以祝融号在火星上受到火星的引力比其在地球上受到的地球引力小,故D正确。
故选D。
8.B
【解析】
【详解】
由
G=mg
得
M=
对平抛运动,水平位移
x=v0t
竖直位移
h=gt2
得
g=
因此得
M=
或
M=
要估算月球质量,还需测量出小石块运动的物理量是抛出的高度h和运动时间t,或者测出抛出的高度h和水平位移x以及初速度v0;
故选B。
9.A
【解析】
【详解】
绕地球表面运动的物体,由牛顿第二定律可知
绕火星表面运动的探测器
解得
故选A。
10.B
【解析】
【详解】
月球绕地球公转做匀速圆周运动,它的向心力由地球引起的,所以在月球绕地球运行的轨道处由地球引力产生的加速度大小就等于月球绕地球做匀速圆周运动的向心力加速度大小,即
根据万有引力等于重力得,在月球表面处由月球引力产生的加速度大小等于月球表面的加速度大小,所以g1、g2、a之间无直接关系。
故选B。
11.D
【解析】
【详解】
由万有引力提供向心力得
①
在天体表面有
②
在该天体表面沿竖直方向以初速度v0向上抛出一个物体,不计阻力,物体上升的过程中的机械能守恒,由机械能守恒定律有
③
由①②③式可知,物体可以到达的最大高度
故选D。
12.D
【解析】
【详解】
A.根据开普勒第二定律可知,B从c经b到d的过程中,速率先减小后增大,故A错误;
B.设地球的质量为M,卫星的质量为m,卫星在半径为r的圆轨道做匀速圆周运动时的速率为v,则根据牛顿第二定律有
解得
设卫星在以Ob为半径的圆轨道上做匀速圆周运动的速率为v2,则由上式可知
根据卫星的变轨特点可知
所以
故B错误;
C.根据牛顿第二定律可知B经过b点时的加速度与A的加速度之比为
故C错误;
D.根据开普勒第三定律可知
故D正确。
故选D。
13.D
【解析】
【详解】
因为飞船在火星表面附近绕火星做匀速圆周运动时,满足
又在天体表面满足
又由自由落体运动规律得
联立解得
故选D。
14.B
【解析】
【详解】
ABC.设地球质量为M,质量为m的物体绕地球做轨道半径为r、周期为T、角速度为ω、线速度为v的匀速圆周运动,根据牛顿第二定律有
分别解得
①
②
③
由于地球同步卫星的轨道高度约为36000km,远大于组合体的轨道高度,根据③式可知组合体的周期小于24小时;根据②式可知组合体的角速度大于同步卫星的角速度;第一宇宙速度是物体在地球表面附近绕地球做匀速圆周运动的速度,而组合体轨道半径大于地球半径,根据①式可知组合体的线速度小于第一宇宙速度,故AC错误,B正确;
D.神舟十三号加速上升阶段,航天员的加速度方向向上,有超重感觉,故D错误。
故选B。
15.B
【解析】
【详解】
由竖直上抛运动和题图可知
,
所以
根据
, ,
得
所以
故选B。
16.
【解析】
【详解】
卫星做圆周运动万有引力提供向心力:,解得:,轨道半径之比;根据万有引力提供向心力:,解得:,它们的周期之比;万有引力为,所受向心力之比.
17.
【解析】
【详解】
根据 ,可得 ,从而知道黄金代换公式.
18.
【解析】
【详解】
物体在地球表面,当忽略自转作用时,所受的万有引力即为重力,有,可得.
【点睛】
掌握求中心天体的质量的两类方法;一是用,二是用环绕天体的转动;解决本题的关键掌握万有引力等于重力这一理论,并能灵活运用.
19.
【解析】
【详解】
设某人造地球卫星质量为m,地球质量为M,沿圆轨道运行时由万有引力提供向心力可得
解得
代入数据解得
20.
【解析】
【分析】
【详解】
在赤道上,万有引力一部分分解为重力,另一部分提供向心力,则有
21.
【解析】
【分析】
实心球挖去一个半径为的小实心球后,质量分布不均匀。因此挖去小实心球剩余的部分,不能看成质量集中于球心的质点,直接求空心球和小实心球之间的万有引力很困难。
【详解】
假设用与挖去的小实心球完全相同的球填补挖去的位置,则空心球变成一个实心球,可看作质量集中于球心的质点,则大、小实心球之间的万有引力为
F=G
小实心球的质量为
m=ρ·π=ρ·πR3=M
代入上式得
F=G
填入的小实心球与挖去的小实心球之间的万有引力为
F1=G=·=
设空心球与小实心球之间的万有引力为F2,则有F=F1+F2因此,空心球与小实心球之间的万有引力为
F2=F-F1=-
22.能,下落的高度和所需时间,
【解析】
【详解】
能估计测出月球的质量
在月球表面用让一重物做自由落体运动,用刻度尺测出下落的高度h,用秒表测量出下落的时间t,根据
求得月球表面的重力加速度,即
根据万有引力等于重力得
月球的质量
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
