人教版数学八年级下册 第十八章 平行四边形 小结与复习课件 (共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册 第十八章 平行四边形 小结与复习课件 (共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 393.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 21:18:47 | ||
图片预览



文档简介
(共15张PPT)
第十八章 平行四边形
小结与复习
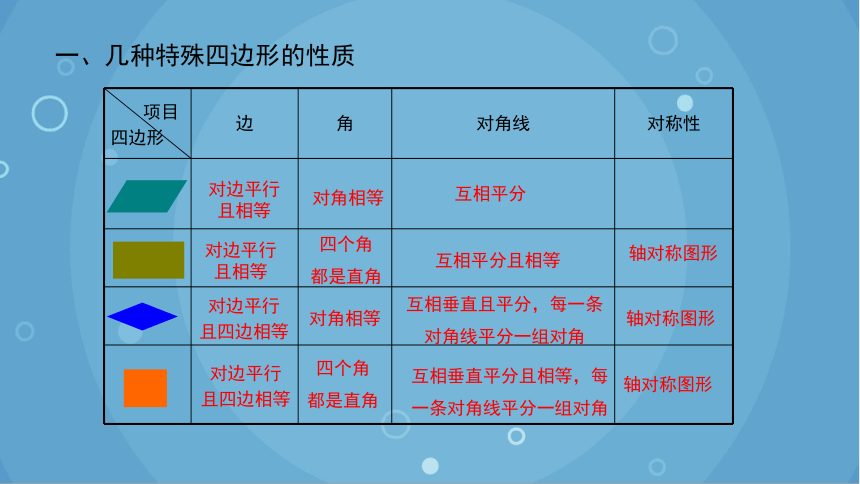
一、几种特殊四边形的性质
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
四边形 条件
平行 四边形
矩形
菱形
正方形
二、几种特殊四边形的常用判定方法:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形,3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
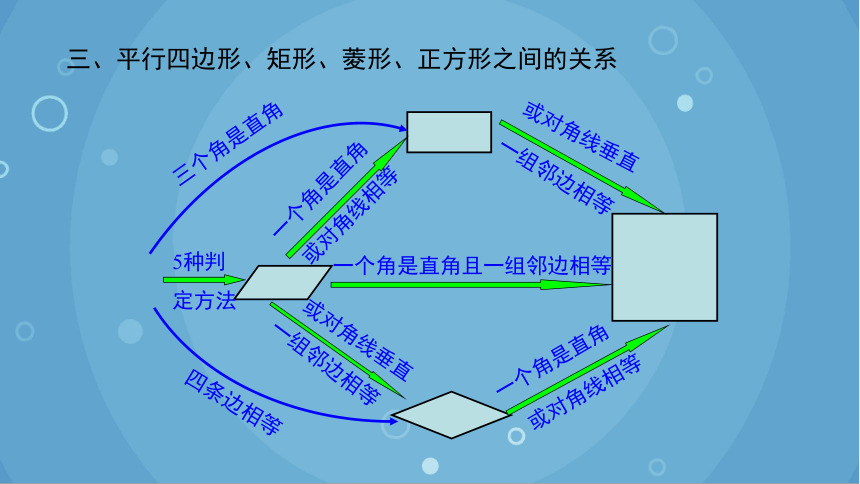
三、平行四边形、矩形、菱形、正方形之间的关系
四、其他重要概念及性质
1.两条平行线之间的距离:
2.三角形的中位线定理:
两条平行线中,一条直线上任意一点到另一条直线的距离叫做两条平行线之间的距离.
三角形的中位线平行于第三边,并且等于第三边的一半.
3.直角三角形斜边上的中线:
直角三角形斜边上的中线等于斜边的一半.
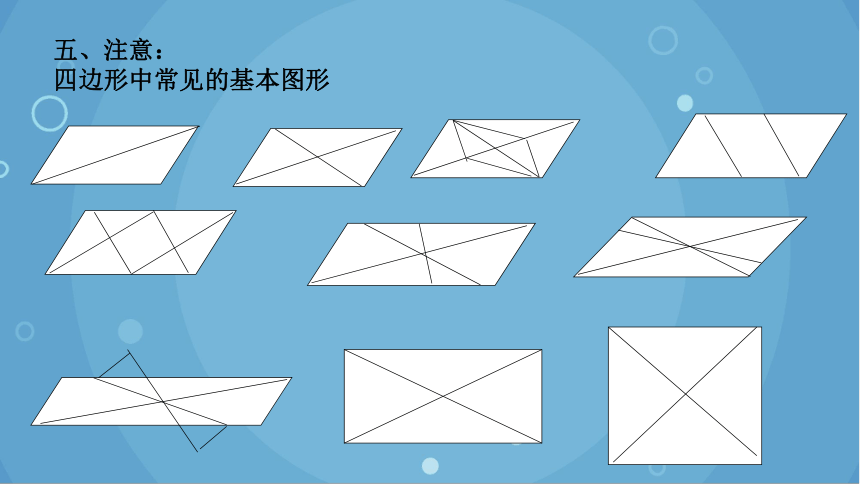
五、注意:
四边形中常见的基本图形
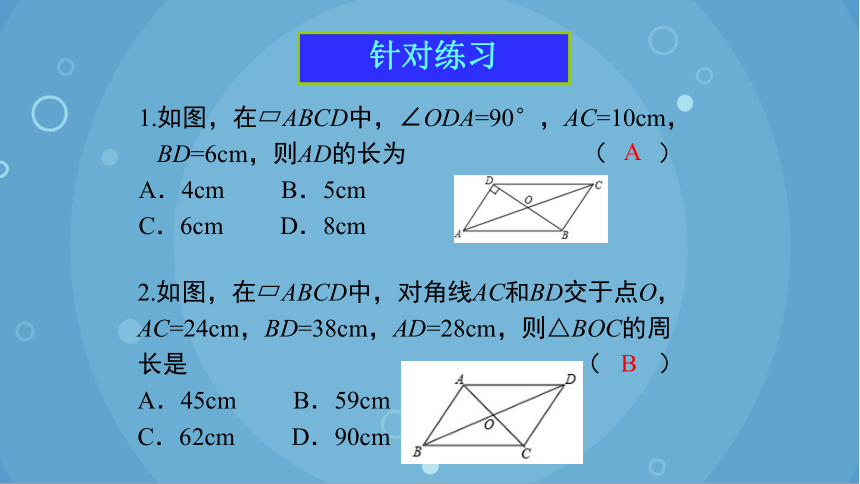
针对练习
2.如图,在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是 ( )
A.45cm B.59cm
C.62cm D.90cm
B
1.如图,在 ABCD中,∠ODA=90°,AC=10cm,
BD=6cm,则AD的长为 ( )
A.4cm B.5cm
C.6cm D.8cm
A
4.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=4m,∠A=30°,则DE等于 ( )
A.1m B.2m
C.3m D.4m
A
3.如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
A.150° B.120°
C.60° D.30°
B
5.如图,两个含有30°角的完全相同的三角板ABC和DEF沿直线FC滑动,下列说法错误的是( )
A.四边形ACDF是平行四边形
B.当点E为BC中点时,四边形ACDF是矩形
C.当点B与点E重合时,四边形ACDF是菱形
D.四边形ACDF不可能是正方形
B
6.如图,在菱形ABCD中,对角线AC=10,BD=6,则菱形ABCD的面积为______.
30
A
B
C
O
D
7.如图 是某公交汽车挡风玻璃的雨刮器,其工作原理如图 .雨刷EF⊥AD,垂足为A,AB=CD,且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC.
又∵EF⊥AD,
∴EF⊥BC.
图
图
8.如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
(1)证明:∵四边形ABCD是正方形,
∴AB=AD.
在△ABE和△DAF中,
∴△ABE≌△DAF.
(2) 解:∵四边形ABCD是正方形,
∴∠1+∠4=90°.
∵∠3=∠4,∴∠1+∠3=90°,
∴∠AFD=90°.
在正方形ABCD中, AD∥BC,
∴∠1=∠AGB=30°.
在Rt△ADF中,∠AFD=90°,AD=2,
∴DF=1,AF= .
由(1)得△ABE≌△DAF,
∴AE=DF=1,
∴EF=AF-AE= -1.
9.如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:
(1)FC的长;(2)EF的长.
解:(1)由题意得AF=AD=10cm,
在Rt△ABF中,∵AB=8,∴BF=6cm,
∴FC=BC-BF=10-6=4(cm).
(2)由题意可得EF=DE,可设DE的长为x,
在Rt△EFC中,(8-x)2+42=x2,
解得x=5,即EF的长为5cm.
10.如图,平行四边形ABCD中,AC、BD为对角线,其交点为O,若BC=6,BC边上的高为4,试求阴影部分的面积.
解:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵AB∥CD,
∴∠EAO=∠HCO.
又∵ ∠AOE=∠COH,
∴△AEO≌△CHO(ASA),
同理可得△OAQ≌△OCG,△OPD≌△OFB,
∴S阴影=S△BCD= S平行四边形ABCD= ×6×4=12.
Q
G
E
H
F
P
11. 在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少.
解:如图,∵在平行四边形ABCD中,AB=CD,AD=BC,AD∥BC,∴∠AEB=∠CBE.
又∵∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE.
(1)当AE=2时,则平行四边形的周长=2×(2+5)=14.
(2)当AE=3时,则平行四边形的周长=2×(3+5)=16.
第十八章 平行四边形
小结与复习
一、几种特殊四边形的性质
项目 四边形 边 角 对角线 对称性
对边平行且相等
对边平行且相等
对边平行
且四边相等
对边平行
且四边相等
对角相等
四个角
都是直角
对角相等
四个角
都是直角
互相平分
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
轴对称图形
轴对称图形
轴对称图形
互相垂直且平分,每一条对角线平分一组对角
四边形 条件
平行 四边形
矩形
菱形
正方形
二、几种特殊四边形的常用判定方法:
1.定义:两组对边分别平行 2.两组对边分别相等
3.两组对角分别相等 4.对角线互相平分
5.一组对边平行且相等
1.定义:有一个角是直角的平行四边形
2.对角线相等的平行四边形
3.有三个角是直角的四边形
1.定义:一组邻边相等的平行四边形 ;2.对角线互相垂直的平行四边形,3.四条边都相等的四边形
1.定义:一组邻边相等且有一个角是直角的平行四边形
2.有一组邻边相等的矩形 3.有一个角是直角的菱形
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
三、平行四边形、矩形、菱形、正方形之间的关系
四、其他重要概念及性质
1.两条平行线之间的距离:
2.三角形的中位线定理:
两条平行线中,一条直线上任意一点到另一条直线的距离叫做两条平行线之间的距离.
三角形的中位线平行于第三边,并且等于第三边的一半.
3.直角三角形斜边上的中线:
直角三角形斜边上的中线等于斜边的一半.
五、注意:
四边形中常见的基本图形
针对练习
2.如图,在 ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是 ( )
A.45cm B.59cm
C.62cm D.90cm
B
1.如图,在 ABCD中,∠ODA=90°,AC=10cm,
BD=6cm,则AD的长为 ( )
A.4cm B.5cm
C.6cm D.8cm
A
4.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=4m,∠A=30°,则DE等于 ( )
A.1m B.2m
C.3m D.4m
A
3.如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
A.150° B.120°
C.60° D.30°
B
5.如图,两个含有30°角的完全相同的三角板ABC和DEF沿直线FC滑动,下列说法错误的是( )
A.四边形ACDF是平行四边形
B.当点E为BC中点时,四边形ACDF是矩形
C.当点B与点E重合时,四边形ACDF是菱形
D.四边形ACDF不可能是正方形
B
6.如图,在菱形ABCD中,对角线AC=10,BD=6,则菱形ABCD的面积为______.
30
A
B
C
O
D
7.如图 是某公交汽车挡风玻璃的雨刮器,其工作原理如图 .雨刷EF⊥AD,垂足为A,AB=CD,且AD=BC,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
证明:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC.
又∵EF⊥AD,
∴EF⊥BC.
图
图
8.如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
(1)证明:∵四边形ABCD是正方形,
∴AB=AD.
在△ABE和△DAF中,
∴△ABE≌△DAF.
(2) 解:∵四边形ABCD是正方形,
∴∠1+∠4=90°.
∵∠3=∠4,∴∠1+∠3=90°,
∴∠AFD=90°.
在正方形ABCD中, AD∥BC,
∴∠1=∠AGB=30°.
在Rt△ADF中,∠AFD=90°,AD=2,
∴DF=1,AF= .
由(1)得△ABE≌△DAF,
∴AE=DF=1,
∴EF=AF-AE= -1.
9.如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:
(1)FC的长;(2)EF的长.
解:(1)由题意得AF=AD=10cm,
在Rt△ABF中,∵AB=8,∴BF=6cm,
∴FC=BC-BF=10-6=4(cm).
(2)由题意可得EF=DE,可设DE的长为x,
在Rt△EFC中,(8-x)2+42=x2,
解得x=5,即EF的长为5cm.
10.如图,平行四边形ABCD中,AC、BD为对角线,其交点为O,若BC=6,BC边上的高为4,试求阴影部分的面积.
解:∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵AB∥CD,
∴∠EAO=∠HCO.
又∵ ∠AOE=∠COH,
∴△AEO≌△CHO(ASA),
同理可得△OAQ≌△OCG,△OPD≌△OFB,
∴S阴影=S△BCD= S平行四边形ABCD= ×6×4=12.
Q
G
E
H
F
P
11. 在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少.
解:如图,∵在平行四边形ABCD中,AB=CD,AD=BC,AD∥BC,∴∠AEB=∠CBE.
又∵∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE.
(1)当AE=2时,则平行四边形的周长=2×(2+5)=14.
(2)当AE=3时,则平行四边形的周长=2×(3+5)=16.
