人教版数学八年级下册专题课堂(二)——利用勾股定理解决问题课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级下册专题课堂(二)——利用勾股定理解决问题课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 365.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 22:40:55 | ||
图片预览



文档简介
(共17张PPT)
数学 八年级下册 人教版
第十七章 勾股定理
专题课堂(二) 利用勾股定理解决问题
一、利用勾股定理解决折叠问题
【例1】如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则AM的长为____.
分析:连接BM,B′M,设AM=A′M=x,在△ABM和△B′DM中,由折叠的性质得BM=B′M,则有x2+92=(9-x)2+(9-3)2,解方程即可得解.
2
【对应训练】
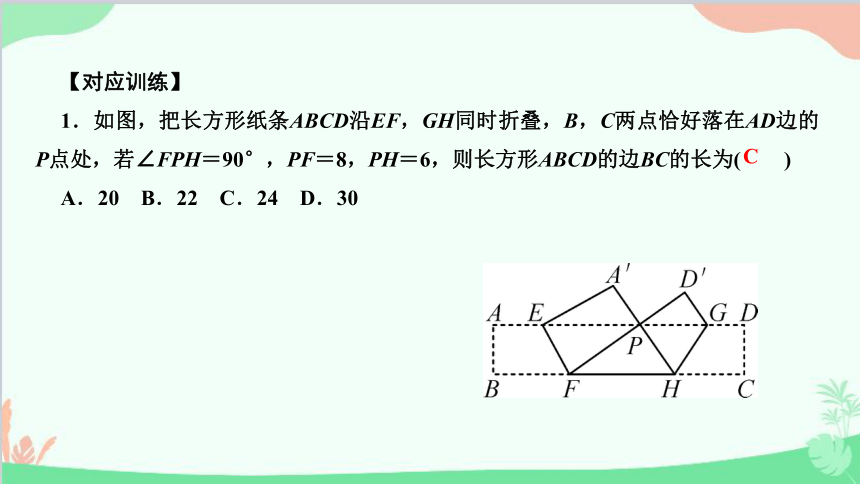
1.如图,把长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的边BC的长为( )
A.20 B.22 C.24 D.30
C
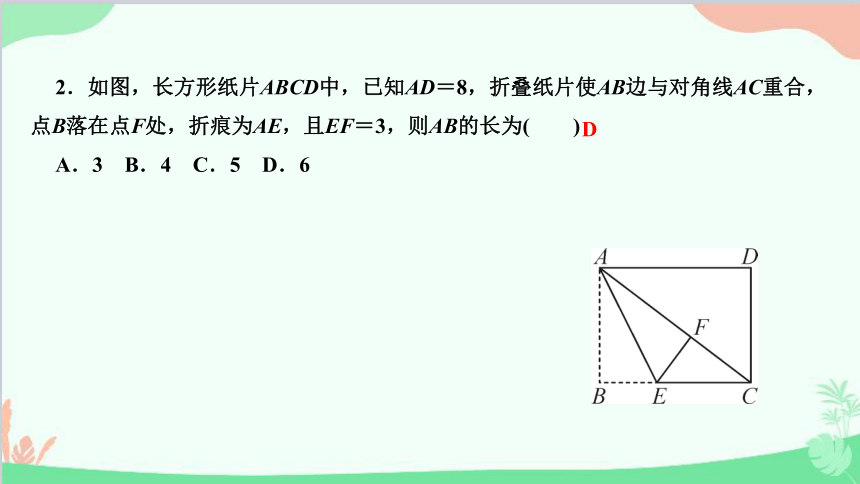
2.如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
D
C
C
A
A
7.如图,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于点E,若AD=8,AB=4,则△BED的面积为______.
10
C
【对应训练】
8.如图,已知∠AOB=45°,点A1,A2,A3……在射线OA上,点B1,B2,B3……在射线OB上,且A1B1⊥OA,A2B2⊥OA,…,AnBn⊥OA;A2B1⊥OB,A3B2⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6……).若OA1=1,则A6B6的长是_____.
32
三、利用勾股定理解决最短路径问题
【例3】如图①,圆柱形玻璃杯的高为12 cm,底面周长为18 cm.在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜处的最短路程为_____ cm.
分析:如图②,将圆柱展开,得到一个长方形,在上面找到A,C两点的位置,根据轴对称的性质和“两点之间,线段最短”可得A′C即为蚂蚁到达蜂蜜处的最短“路线”,再利用勾股定理求出A′C的长度即可.
15
【对应训练】
9.如图,在一个长为2 m,宽为1 m的长方形场地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达点C处需要走的最短路程是_____m.
2.6
10.如图①的正方体木块棱长为6 cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短路程为__________cm.
四、利用勾股定理的逆定理判定三角形的形状
【例4】已知两条线段的长分别为15和8,当第三条线段取整数____时,这三条线段能围成一个直角三角形.
分析:由于直角三角形的斜边不能确定,故应分15为直角边和斜边两种情况进行讨论.
17
【对应训练】
11.若三角形的三边长为a,b,c,且满足等式(a+b)2-c2=2ab,则此三角形是_______三角形.(填“直角”“锐角”或“钝角”)
12.若边长为a的正方形的面积等于长为b+c,宽为b-c的长方形的面积,则以a,b,c为三边长的三角形是_______三角形.
13.已知△ABC的三边为a,b,c,且a+b=7,ab=12,c=5,试判定△ABC的形状.
解:∵a2+b2=(a+b)2-2ab=25,c2=25,∴a2+b2=c2,∴△ABC是直角三角形
直角
直角
数学 八年级下册 人教版
第十七章 勾股定理
专题课堂(二) 利用勾股定理解决问题
一、利用勾股定理解决折叠问题
【例1】如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则AM的长为____.
分析:连接BM,B′M,设AM=A′M=x,在△ABM和△B′DM中,由折叠的性质得BM=B′M,则有x2+92=(9-x)2+(9-3)2,解方程即可得解.
2
【对应训练】
1.如图,把长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的边BC的长为( )
A.20 B.22 C.24 D.30
C
2.如图,长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3 B.4 C.5 D.6
D
C
C
A
A
7.如图,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于点E,若AD=8,AB=4,则△BED的面积为______.
10
C
【对应训练】
8.如图,已知∠AOB=45°,点A1,A2,A3……在射线OA上,点B1,B2,B3……在射线OB上,且A1B1⊥OA,A2B2⊥OA,…,AnBn⊥OA;A2B1⊥OB,A3B2⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6……).若OA1=1,则A6B6的长是_____.
32
三、利用勾股定理解决最短路径问题
【例3】如图①,圆柱形玻璃杯的高为12 cm,底面周长为18 cm.在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜处的最短路程为_____ cm.
分析:如图②,将圆柱展开,得到一个长方形,在上面找到A,C两点的位置,根据轴对称的性质和“两点之间,线段最短”可得A′C即为蚂蚁到达蜂蜜处的最短“路线”,再利用勾股定理求出A′C的长度即可.
15
【对应训练】
9.如图,在一个长为2 m,宽为1 m的长方形场地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达点C处需要走的最短路程是_____m.
2.6
10.如图①的正方体木块棱长为6 cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短路程为__________cm.
四、利用勾股定理的逆定理判定三角形的形状
【例4】已知两条线段的长分别为15和8,当第三条线段取整数____时,这三条线段能围成一个直角三角形.
分析:由于直角三角形的斜边不能确定,故应分15为直角边和斜边两种情况进行讨论.
17
【对应训练】
11.若三角形的三边长为a,b,c,且满足等式(a+b)2-c2=2ab,则此三角形是_______三角形.(填“直角”“锐角”或“钝角”)
12.若边长为a的正方形的面积等于长为b+c,宽为b-c的长方形的面积,则以a,b,c为三边长的三角形是_______三角形.
13.已知△ABC的三边为a,b,c,且a+b=7,ab=12,c=5,试判定△ABC的形状.
解:∵a2+b2=(a+b)2-2ab=25,c2=25,∴a2+b2=c2,∴△ABC是直角三角形
直角
直角
