北师大版数学八年级下册 1.1等腰三角形的判定(第3课时)课件 (共16张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 1.1等腰三角形的判定(第3课时)课件 (共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 07:55:11 | ||
图片预览




文档简介
(共17张PPT)
第一章 三角形的证明
1.1 等腰三角形
第3课时 等腰三角形的判定
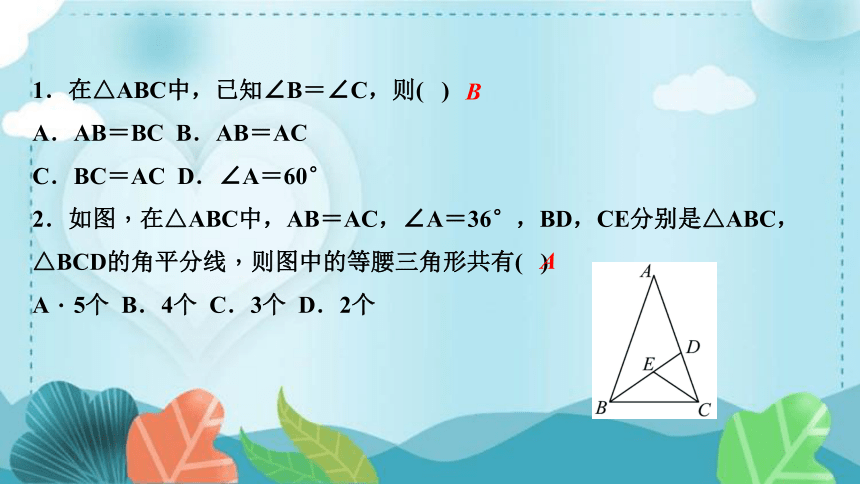
1.在△ABC中,已知∠B=∠C,则( )
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别是△ABC,△BCD的角平分线,则图中的等腰三角形共有( )
A.5个 B.4个 C.3个 D.2个
B
A
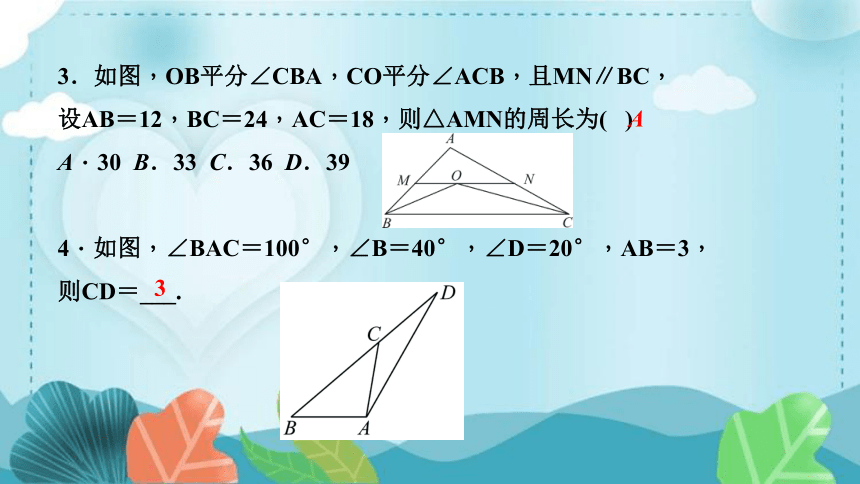
3.如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,
设AB=12,BC=24,AC=18,则△AMN的周长为( )
A.30 B.33 C.36 D.39
4.如图,∠BAC=100°,∠B=40°,∠D=20°,AB=3,
则CD=___.
A
3
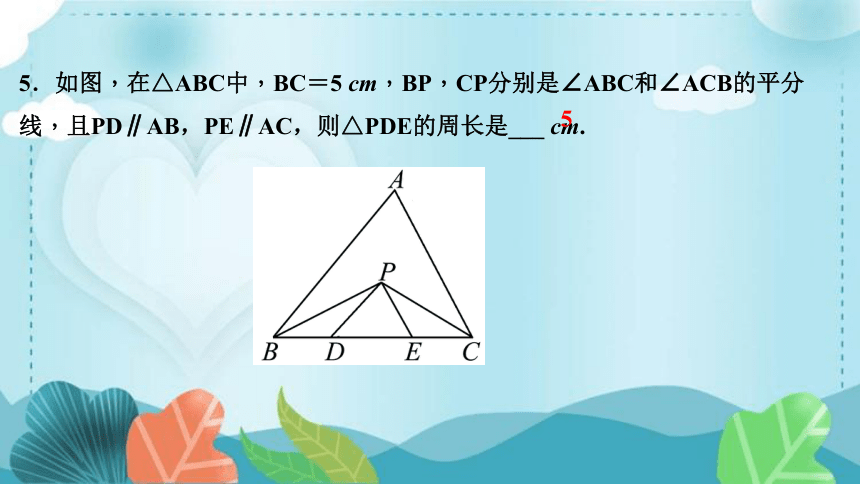
5.如图,在△ABC中,BC=5 cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是___ cm.
5
6.用反证法证明命题“在三角形中,至多有一个内角是直角”时,
应先假设( )
A.至少有一个内角是直角
B.至少有两个内角是直角
C.至多有一个内角是直角
D.至多有两个内角是直角
7.请举反例说明命题“对于任意实数x,x2+5x+5的值总是正数”
是假命题.你举的反例是____.(写出一个x的值即可)
B
-2
8.用反证法证明:等腰三角形的两底角必为锐角.
已知:△ABC,AB=AC.
求证:∠B,∠C都是锐角.
证明:①假设等腰三角形的底角∠B,∠C都是直角,
则_________________,
从而___________________>180°,
这与___________________矛盾;
∠B+∠C=180°
∠A+∠B+∠C
三角形内角和定理
②设等腰三角形的底角∠B,∠C都是钝角,
则_______________________,
从而___________________________,
这与______________________矛盾.
综上所述,假设①,②_______,
所以∠B,∠C只能为_____,
故等腰三角形的两底角必为锐角.
∠B+∠C>180°
∠A+∠B+∠C>180°
三角形内角和定理
不成立
锐角
C
10.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
A.40海里 B.60海里 C.70海里 D.80海里
D
11.如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.
给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):______________.
①③或②③
12.用反证法证明:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC
求证:∠A,∠B,∠C中至少有一个角小于或等于60°.
证明:假设∠A,∠B,∠C中没有一个内角小于或等于60°.
即∠A____60°,∠B____60°,∠C____60°,
∴∠A+∠B+∠C___180°,这与三角形的内角和等于180°____,
∴∠A,∠B,∠C中至少有一个内角小于或等于60°.
>
>
>
>
矛盾
13.如图,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
解:OE和AB相互垂直.理由:在△ABC和△BAD中,AB=BA,
∠BAC=∠ABD,AC=BD,∴△ABC≌△BAD(SAS),
∴∠ABC=∠BAD,∴OA=OB,∵点E是AB的中点,∴OE⊥AB
14.如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
证明:
∵DE∥AC,∴∠1=∠3,∵AD平分∠BAC,
∴∠1=∠2,∴∠2=∠3,∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°,
∴∠B=∠BDE,∴BE=DE,∴△BDE是等腰三角形
15.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=________,∠DEC=________;点D从B向C运动时,∠BDA逐渐变________(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?
若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
解:(1)25° 115° 小
(2)当DC=2时,△ABD≌△DCE.理由:∵∠C=40°,
∴∠DEC+∠EDC=140°.又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC.
又∵AB=DC=2,∴△ABD≌△DCE(AAS)
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
理由:当∠BDA=110°时,∠ADC=70°.∵∠C=40°,
∴∠DAC=180°-∠ADC-∠C=180°-70°-40°=70°,
∴∠AED=180°-∠DAC-∠ADE=180°-70°-40°=70°,
∴∠AED=∠DAE,∴AD=ED,∴△ADE的形状是等腰三角形.
当∠BDA=80°时,∠ADC=100°.
∴∠DAC=180°-∠ADC-∠C=180°-100°-40°=40°,
∴∠DAE=∠ADE,∴AE=DE,∴△ADE的形状是等腰三角形
第一章 三角形的证明
1.1 等腰三角形
第3课时 等腰三角形的判定
1.在△ABC中,已知∠B=∠C,则( )
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别是△ABC,△BCD的角平分线,则图中的等腰三角形共有( )
A.5个 B.4个 C.3个 D.2个
B
A
3.如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,
设AB=12,BC=24,AC=18,则△AMN的周长为( )
A.30 B.33 C.36 D.39
4.如图,∠BAC=100°,∠B=40°,∠D=20°,AB=3,
则CD=___.
A
3
5.如图,在△ABC中,BC=5 cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是___ cm.
5
6.用反证法证明命题“在三角形中,至多有一个内角是直角”时,
应先假设( )
A.至少有一个内角是直角
B.至少有两个内角是直角
C.至多有一个内角是直角
D.至多有两个内角是直角
7.请举反例说明命题“对于任意实数x,x2+5x+5的值总是正数”
是假命题.你举的反例是____.(写出一个x的值即可)
B
-2
8.用反证法证明:等腰三角形的两底角必为锐角.
已知:△ABC,AB=AC.
求证:∠B,∠C都是锐角.
证明:①假设等腰三角形的底角∠B,∠C都是直角,
则_________________,
从而___________________>180°,
这与___________________矛盾;
∠B+∠C=180°
∠A+∠B+∠C
三角形内角和定理
②设等腰三角形的底角∠B,∠C都是钝角,
则_______________________,
从而___________________________,
这与______________________矛盾.
综上所述,假设①,②_______,
所以∠B,∠C只能为_____,
故等腰三角形的两底角必为锐角.
∠B+∠C>180°
∠A+∠B+∠C>180°
三角形内角和定理
不成立
锐角
C
10.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
A.40海里 B.60海里 C.70海里 D.80海里
D
11.如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.
给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):______________.
①③或②③
12.用反证法证明:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC
求证:∠A,∠B,∠C中至少有一个角小于或等于60°.
证明:假设∠A,∠B,∠C中没有一个内角小于或等于60°.
即∠A____60°,∠B____60°,∠C____60°,
∴∠A+∠B+∠C___180°,这与三角形的内角和等于180°____,
∴∠A,∠B,∠C中至少有一个内角小于或等于60°.
>
>
>
>
矛盾
13.如图,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
解:OE和AB相互垂直.理由:在△ABC和△BAD中,AB=BA,
∠BAC=∠ABD,AC=BD,∴△ABC≌△BAD(SAS),
∴∠ABC=∠BAD,∴OA=OB,∵点E是AB的中点,∴OE⊥AB
14.如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
证明:
∵DE∥AC,∴∠1=∠3,∵AD平分∠BAC,
∴∠1=∠2,∴∠2=∠3,∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°,
∴∠B=∠BDE,∴BE=DE,∴△BDE是等腰三角形
15.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=________,∠DEC=________;点D从B向C运动时,∠BDA逐渐变________(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?
若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
解:(1)25° 115° 小
(2)当DC=2时,△ABD≌△DCE.理由:∵∠C=40°,
∴∠DEC+∠EDC=140°.又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC.
又∵AB=DC=2,∴△ABD≌△DCE(AAS)
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
理由:当∠BDA=110°时,∠ADC=70°.∵∠C=40°,
∴∠DAC=180°-∠ADC-∠C=180°-70°-40°=70°,
∴∠AED=180°-∠DAC-∠ADE=180°-70°-40°=70°,
∴∠AED=∠DAE,∴AD=ED,∴△ADE的形状是等腰三角形.
当∠BDA=80°时,∠ADC=100°.
∴∠DAC=180°-∠ADC-∠C=180°-100°-40°=40°,
∴∠DAE=∠ADE,∴AE=DE,∴△ADE的形状是等腰三角形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
