贵州省湄潭中学2013届高三上学期期末考试 文数试题 无答案
文档属性
| 名称 | 贵州省湄潭中学2013届高三上学期期末考试 文数试题 无答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-21 00:00:00 | ||
图片预览




文档简介
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷
命题人:简仕扬
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x},B={x}},则AB=
(A) {x} (B){x} (C){x} (D){x}
2.若,为虚数单位,且则
A., B. C. D.
3. “”是“” 的
A.充分不必要条件 B.必要不充分条件
C. 充分必要条件 D.既不充分又不必要条件
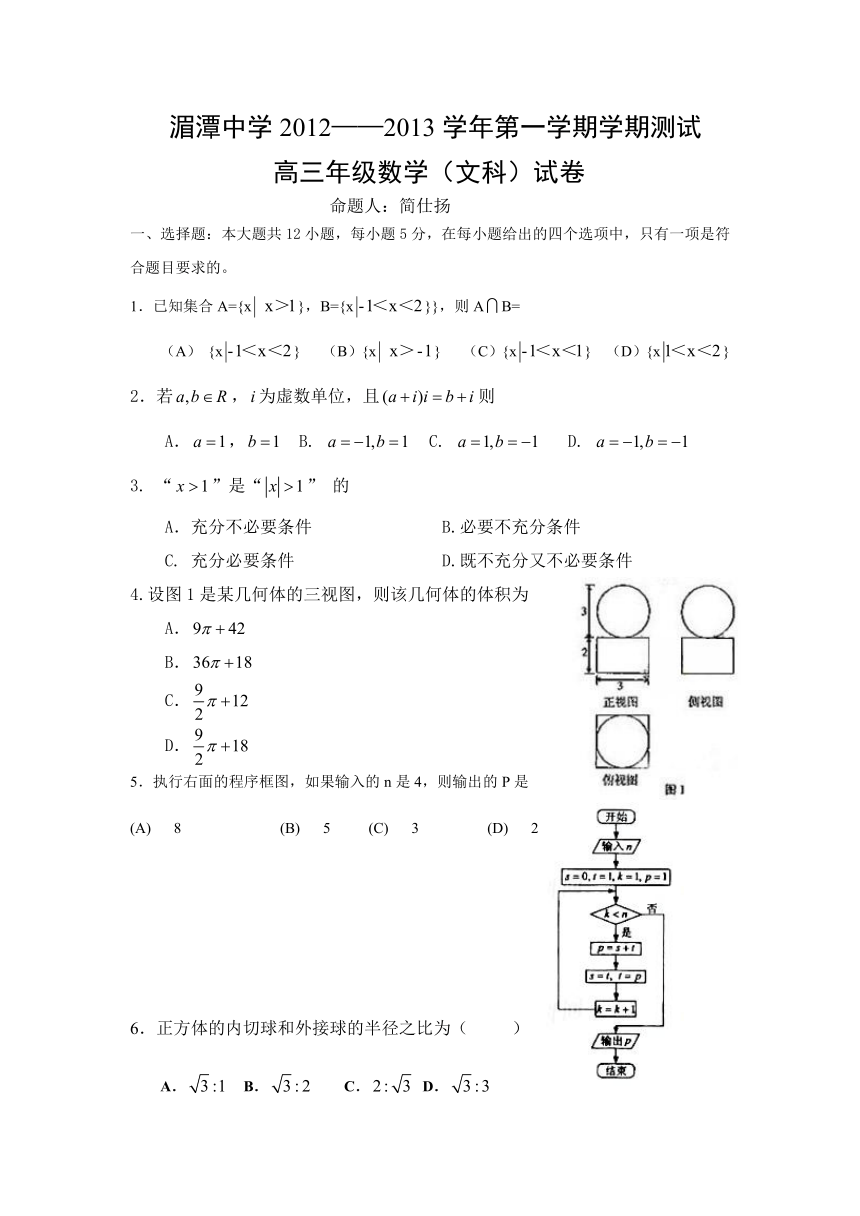
4.设图1是某几何体的三视图,则该几何体的体积为
A.
B.
C.
D.
5.执行右面的程序框图,如果输入的n是4,则输出的P是
(A) 8 (B) 5 (C) 3 (D) 2
6.正方体的内切球和外接球的半径之比为( )
A. B. C. D.
7.在中,,.若点满足,则( )
A. B. C. D.
8.已知等差数列满足,,则它的前10项的和( )
A.138 B.135 C.95 D.23
9.设曲线在点处的切线与直线垂直,则( )
A.2 B. C. D.
10.容量为的样本数据,按从小到大的顺序分为组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是 ( )
A.和 B.和 C. 和 D. 和
11.双曲线的渐近线与圆相切,则r=
(A) (B)2 (C)3 (D)6
12.已知直线与抛物线C:相交A、B两点,F为C的焦点。若,则k=
(A) (B) (C) (D)
二、填空题:(每小题5分,共20分,把答案填在答题卡中对应号后的横线上。)
13.在区间中随机地取出两个数,则两数之和小于的概率是______________。
14.已知辆汽车通过某一段公路时的时速的频率
分布直方图如右图所示,则时速在的汽车
大约有__辆。
15.如果,则的最大值是______________。
16.设是球的半径,是的中点,过且与成45°角的平面截球的表面得到圆。若圆的面积等于,则球的表面积等于. ______________。
三.解答题:本大题共6小题,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足c.sinA=a.cosC.
求角C的大小;
求sinA-cos (B+)的最大值,并求取得最大值时角A、B的大小。
18.(本小题满分12分)
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD。
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
19.(本小题满分12分)
某车间甲组有10名工人,其中有3名女工人;乙组有5名工人,其中有3名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
20. 如图,设P是圆上的动点,点D是P在x轴上的投影,M为PD上一点,且
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为的直线被C所截线段的长度
21.已知数列满足:,且
(1)设,证明数列是等差数列;
(2)求数列、的通项公式;
22.设.
(1)若在上存在单调递增区间,求的取值范围;
(2)当时,在上的最小值为,求在该区间上的最大值.
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷考试试题答题卡
一.选择题.(每小题5分)
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题5分)
1,——, 2,——
3,—— 4,——
三、解答题(1题10分,其余每个12分)
17.(本小题满分10分)
18.(本小题满分12分)
19.
20
21.
22
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷
命题人:简仕扬
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x},B={x}},则AB=
(A) {x} (B){x} (C){x} (D){x}
2.若,为虚数单位,且则
A., B. C. D.
3. “”是“” 的
A.充分不必要条件 B.必要不充分条件
C. 充分必要条件 D.既不充分又不必要条件
4.设图1是某几何体的三视图,则该几何体的体积为
A.
B.
C.
D.
5.执行右面的程序框图,如果输入的n是4,则输出的P是
(A) 8 (B) 5 (C) 3 (D) 2
6.正方体的内切球和外接球的半径之比为( )
A. B. C. D.
7.在中,,.若点满足,则( )
A. B. C. D.
8.已知等差数列满足,,则它的前10项的和( )
A.138 B.135 C.95 D.23
9.设曲线在点处的切线与直线垂直,则( )
A.2 B. C. D.
10.容量为的样本数据,按从小到大的顺序分为组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是 ( )
A.和 B.和 C. 和 D. 和
11.双曲线的渐近线与圆相切,则r=
(A) (B)2 (C)3 (D)6
12.已知直线与抛物线C:相交A、B两点,F为C的焦点。若,则k=
(A) (B) (C) (D)
二、填空题:(每小题5分,共20分,把答案填在答题卡中对应号后的横线上。)
13.在区间中随机地取出两个数,则两数之和小于的概率是______________。
14.已知辆汽车通过某一段公路时的时速的频率
分布直方图如右图所示,则时速在的汽车
大约有__辆。
15.如果,则的最大值是______________。
16.设是球的半径,是的中点,过且与成45°角的平面截球的表面得到圆。若圆的面积等于,则球的表面积等于. ______________。
三.解答题:本大题共6小题,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足c.sinA=a.cosC.
求角C的大小;
求sinA-cos (B+)的最大值,并求取得最大值时角A、B的大小。
18.(本小题满分12分)
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD。
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
19.(本小题满分12分)
某车间甲组有10名工人,其中有3名女工人;乙组有5名工人,其中有3名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
20. 如图,设P是圆上的动点,点D是P在x轴上的投影,M为PD上一点,且
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为的直线被C所截线段的长度
21.已知数列满足:,且
(1)设,证明数列是等差数列;
(2)求数列、的通项公式;
22.设.
(1)若在上存在单调递增区间,求的取值范围;
(2)当时,在上的最小值为,求在该区间上的最大值.
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷考试试题答题卡
一.选择题.(每小题5分)
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题5分)
1,——, 2,——
3,—— 4,——
三、解答题(1题10分,其余每个12分)
17.(本小题满分10分)
18.(本小题满分12分)
19.
20
21.
22
高三年级数学(文科)试卷
命题人:简仕扬
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x},B={x}},则AB=
(A) {x} (B){x} (C){x} (D){x}
2.若,为虚数单位,且则
A., B. C. D.
3. “”是“” 的
A.充分不必要条件 B.必要不充分条件
C. 充分必要条件 D.既不充分又不必要条件
4.设图1是某几何体的三视图,则该几何体的体积为
A.
B.
C.
D.
5.执行右面的程序框图,如果输入的n是4,则输出的P是
(A) 8 (B) 5 (C) 3 (D) 2
6.正方体的内切球和外接球的半径之比为( )
A. B. C. D.
7.在中,,.若点满足,则( )
A. B. C. D.
8.已知等差数列满足,,则它的前10项的和( )
A.138 B.135 C.95 D.23
9.设曲线在点处的切线与直线垂直,则( )
A.2 B. C. D.
10.容量为的样本数据,按从小到大的顺序分为组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是 ( )
A.和 B.和 C. 和 D. 和
11.双曲线的渐近线与圆相切,则r=
(A) (B)2 (C)3 (D)6
12.已知直线与抛物线C:相交A、B两点,F为C的焦点。若,则k=
(A) (B) (C) (D)
二、填空题:(每小题5分,共20分,把答案填在答题卡中对应号后的横线上。)
13.在区间中随机地取出两个数,则两数之和小于的概率是______________。
14.已知辆汽车通过某一段公路时的时速的频率
分布直方图如右图所示,则时速在的汽车
大约有__辆。
15.如果,则的最大值是______________。
16.设是球的半径,是的中点,过且与成45°角的平面截球的表面得到圆。若圆的面积等于,则球的表面积等于. ______________。
三.解答题:本大题共6小题,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足c.sinA=a.cosC.
求角C的大小;
求sinA-cos (B+)的最大值,并求取得最大值时角A、B的大小。
18.(本小题满分12分)
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD。
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
19.(本小题满分12分)
某车间甲组有10名工人,其中有3名女工人;乙组有5名工人,其中有3名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
20. 如图,设P是圆上的动点,点D是P在x轴上的投影,M为PD上一点,且
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为的直线被C所截线段的长度
21.已知数列满足:,且
(1)设,证明数列是等差数列;
(2)求数列、的通项公式;
22.设.
(1)若在上存在单调递增区间,求的取值范围;
(2)当时,在上的最小值为,求在该区间上的最大值.
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷考试试题答题卡
一.选择题.(每小题5分)
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题5分)
1,——, 2,——
3,—— 4,——
三、解答题(1题10分,其余每个12分)
17.(本小题满分10分)
18.(本小题满分12分)
19.
20
21.
22
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷
命题人:简仕扬
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x},B={x}},则AB=
(A) {x} (B){x} (C){x} (D){x}
2.若,为虚数单位,且则
A., B. C. D.
3. “”是“” 的
A.充分不必要条件 B.必要不充分条件
C. 充分必要条件 D.既不充分又不必要条件
4.设图1是某几何体的三视图,则该几何体的体积为
A.
B.
C.
D.
5.执行右面的程序框图,如果输入的n是4,则输出的P是
(A) 8 (B) 5 (C) 3 (D) 2
6.正方体的内切球和外接球的半径之比为( )
A. B. C. D.
7.在中,,.若点满足,则( )
A. B. C. D.
8.已知等差数列满足,,则它的前10项的和( )
A.138 B.135 C.95 D.23
9.设曲线在点处的切线与直线垂直,则( )
A.2 B. C. D.
10.容量为的样本数据,按从小到大的顺序分为组,如下表:
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
第三组的频数和频率分别是 ( )
A.和 B.和 C. 和 D. 和
11.双曲线的渐近线与圆相切,则r=
(A) (B)2 (C)3 (D)6
12.已知直线与抛物线C:相交A、B两点,F为C的焦点。若,则k=
(A) (B) (C) (D)
二、填空题:(每小题5分,共20分,把答案填在答题卡中对应号后的横线上。)
13.在区间中随机地取出两个数,则两数之和小于的概率是______________。
14.已知辆汽车通过某一段公路时的时速的频率
分布直方图如右图所示,则时速在的汽车
大约有__辆。
15.如果,则的最大值是______________。
16.设是球的半径,是的中点,过且与成45°角的平面截球的表面得到圆。若圆的面积等于,则球的表面积等于. ______________。
三.解答题:本大题共6小题,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足c.sinA=a.cosC.
求角C的大小;
求sinA-cos (B+)的最大值,并求取得最大值时角A、B的大小。
18.(本小题满分12分)
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD。
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值。
19.(本小题满分12分)
某车间甲组有10名工人,其中有3名女工人;乙组有5名工人,其中有3名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
20. 如图,设P是圆上的动点,点D是P在x轴上的投影,M为PD上一点,且
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为的直线被C所截线段的长度
21.已知数列满足:,且
(1)设,证明数列是等差数列;
(2)求数列、的通项公式;
22.设.
(1)若在上存在单调递增区间,求的取值范围;
(2)当时,在上的最小值为,求在该区间上的最大值.
湄潭中学2012——2013学年第一学期学期测试
高三年级数学(文科)试卷考试试题答题卡
一.选择题.(每小题5分)
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题(每小题5分)
1,——, 2,——
3,—— 4,——
三、解答题(1题10分,其余每个12分)
17.(本小题满分10分)
18.(本小题满分12分)
19.
20
21.
22
同课章节目录
