2021-2022学年数学六年级下册 小升初专项 立体图形(讲义) (含简单答案)
文档属性
| 名称 | 2021-2022学年数学六年级下册 小升初专项 立体图形(讲义) (含简单答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览



文档简介
专项六:立体图形
【课程目标】
1、掌握立体图形切割拼补后表面积和体积的变化
2、掌握运用等积法求不规则图形的体积
3、培养学生的空间思维能力及细心习惯
知识点一:按比例分配
【例1】已知长方体的棱长总和为36厘米,长、宽、高之比为4:3:2,求这个长方体的体积和表面积。
【变式训练1】
1、一个长方体的长、宽、高的比是3:2:1,已知长方体的棱长总和是144厘米,它的体积是 .表面积是 .
2、已知长方体的长是宽的2倍,高是宽的3倍,棱长总和为48厘米,这个长方体的体积是_________,表面积是__________。
3、一个长方体棱长总和是96厘米,长比宽多25%,高比宽少,这个长方体的体积是_________,表面积是__________。
知识点二:立体图形和比的应用
【例2】甲、乙两个圆柱体底面半径的比是2:3,体积比是5:6,甲、乙两个圆柱高的比是 .
【变式训练2】
1、一个圆柱体和一个圆锥体,半径之比是1:2,高之比是2:5,它们体积之比为 .
2、有两个底面半径相等的圆柱和圆锥,高的比是4:5,圆柱的体积是60立方厘米,则圆锥的体积是______立方厘米。
3、圆柱体和圆锥体的底面半径的比是2:3,则圆柱与圆锥的体积比是16:9,求圆柱的高和圆锥的高的比是______:_________.
知识点三:表面积和体积的变化
【例3】一个长方体,如果它的长和宽都扩大4倍,高变为原来的,那么这个长方体的体积扩大 倍.
【变式训练3】
1、长方体的长和宽都增加3倍,高不变,则它的体积变为原来的_______倍
2、长方体的长为5cm,宽为4cm,高为3cm,将长方体的长增加,宽减少,高扩大两倍,求所得长方形的体积比原来的多_______.
3、一个圆锥,增加后的高与原来的高的比是8:3.如果圆锥的体积不变,原来的底面积比现在的底面积大40cm2.现在的底面积是__________.
【例4】如图,长方体的长20厘米,宽10厘米,高5厘米.在长方体的一角去掉一个棱长5厘米的正方体.求剩下部分的表面积是多少?
【变式训练4】
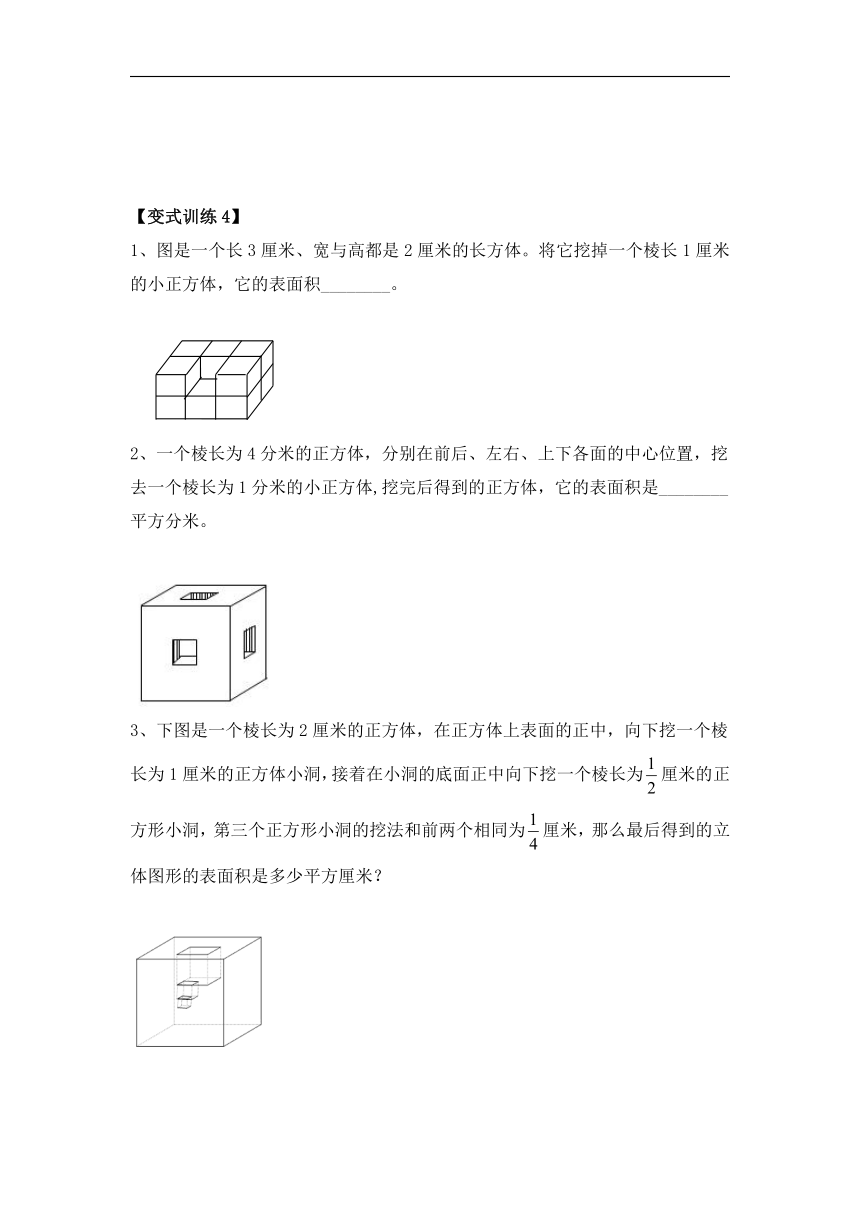
1、图是一个长3厘米、宽与高都是2厘米的长方体。将它挖掉一个棱长1厘米的小正方体,它的表面积________。
2、一个棱长为4分米的正方体,分别在前后、左右、上下各面的中心位置,挖去一个棱长为1分米的小正方体,挖完后得到的正方体,它的表面积是________平方分米。
3、下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为厘米,那么最后得到的立体图形的表面积是多少平方厘米?
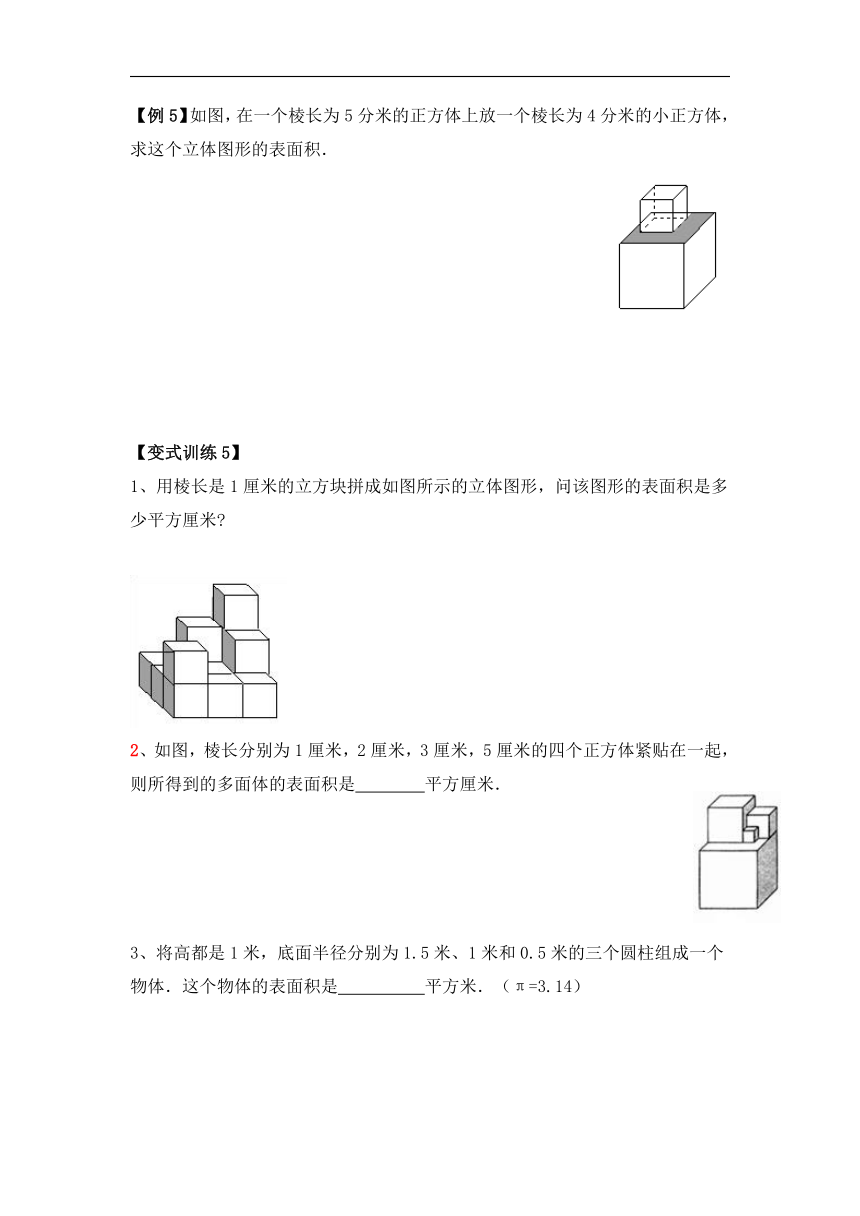
【例5】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.
【变式训练5】
1、用棱长是1厘米的立方块拼成如图所示的立体图形,问该图形的表面积是多少平方厘米
2、如图,棱长分别为1厘米,2厘米,3厘米,5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是 平方厘米.
3、将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.这个物体的表面积是 平方米.(π=3.14)
【例6】一个长方体,如果高增加3厘米,就成为一个正方体.这时表面积比原来增加了96平方厘米。原来的长方体的体积是多少立方厘米?
【变式训练6】
1、一个长方体,如宽增加2厘米,就成了正方体,而且表面积增加56平方厘米,原来这个长方体的体积是______立方厘米。
2、一个长方体木块,从中间截去高为5厘米长方体后,合并后便成为一个正方体,表面积减少了120平方厘米,原长方体的体积是__________立方厘米.
3、一个长方体,如果长增加2厘米,则体积增加40立方厘米,如果宽增加3厘米,则体积增加90立方厘米,如果高增加4厘米,则体积增加96立方厘米,原长方体的表面积是___________平方厘米.
【例7】如右图所示,这根石柱子的体积是 立方米.
答案:如图,假设再有一个一模一样的立体图形,即可拼接成一个高为28cm的圆柱体,求出圆柱体体积再除以2即可.
【变式训练7】
1、计算下面图形的体积
2、如图1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:厘米).将它们拼成如图2的新几何体,则该新几何体的体积应为 立方厘米.
知识点四:切割、拼补立体图形
【例8】把2.4米长的长方体木料,平均锯成3段,表面积比原来增加了4.8平方分米,原来这根木料的体积是多少立方分米?
【变式训练8】
1、把一根长1 米的木料平均截成4段后,表面积增加了36平方厘米,原来这根木料的体积是 .
2、一个正方体体积是8dm3,把它平均分成4个长方体.表面积增加 dm2.
3、如图,一段圆柱形木料,如果截成两个小圆柱,它的表面积将增加6.28平方厘米,如果沿直径截成两个半圆柱,它的表面积将增加80平方厘米,求原圆柱的体积。
【例9】把3个棱长4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是 cm2.
【变式训练9】
1、把3个棱长为10分米的正方体拼成一个长方体,表面积会减少 平方厘米,长方体的体积是 立方厘米。
2、把3个正方体木块粘合成一个长方体,这个长方体的表面积会减少16cm2,求原正方体体积是 .
3、用3个相同的长方体木料拼成一个大长方体,每根的长是15厘米,宽是11厘米,高是7厘米.怎样拼才能使得拼成的长方体的表面积最大?最少是多少平方厘米?
知识点五:等积法
【例10】如图,一个长方体玻璃容器,从里面量长为3分米,宽为3分米,高4分米。向容器中倒入18升水,再把一个苹果放入水中,这时测得容器内的水面的高度是21厘米。这个苹果的体积是多少?
【变式训练10】
1、一个底面积1.5平方分米的玻璃缸里有一块石头,如图所示.水深18厘米,拿出石块后水面下降到15厘米,这块石头体积是多少?
2、有一种饮料瓶,如图所示,瓶身呈圆柱形,容积是600毫升。现在瓶中装有一些饮料,正放时饮料髙度为12厘米,倒放时空余部分的高度为4厘米。问:瓶内现有饮料多少立方厘米?
3、一个长方体玻璃杯中盛有水,水的高度是2.5厘米,玻璃杯内侧的底面积是72平方厘米,在这个杯中放进一个6厘米的正方体铁块后,铁块没有完全浸没,求这时水的高度是多少?
【例11】 棱长是6分米的正方体容器装满水,把容器里的水全部倒入一个长方体水箱,水箱从里面量长6分米,宽5分米,高8.5分米,这时倒入水箱里面的水深是多少分米?再要注满水箱应倒入多少升水?
【变式训练11】
1、一个棱长8分米的正方体水槽里装了490升水,把这些水倒入一个长10分米,宽7分米,高8分米的长方体水槽里,水槽里的水深是多少?
2、一个底面积为40cm,高6cm的圆锥体容器,装满水后全部倒入一个棱长为5cm的正方体容器里,水深多少厘米?
3、在甲箱中装入水,深度为15厘米,放进一个长10厘米宽9厘米,高5厘米的小正方体A,则水升高多少厘米? 若将这些水和物体A一起倒入乙箱,水深为多少厘米
知识点六:圆柱圆锥
【例12】等底等高的圆柱和圆锥,它们的体积之和是48立方厘米,则这个圆柱的体积是 立方厘米,圆锥的体积是 立方厘米.
【变式训练12】
1、一个圆柱和一个圆锥等底等高,它们的体积之差是24dm3,那么圆锥的体积是 dm3,圆柱的体积是 m3。
2、一个长方体木料,横截面是边长10厘米的正方形。从这根木料上截下6厘米长的一段,切削成一个最大的圆锥,圆锥的体积是 立方厘米,削去部分体积是 立方厘米。
3、下图为一个棱长6厘米的正方体,从正方体的底面向内挖一个最大的圆锥,剩下的体积是多少立方厘米?
【拓展提高】
1、有一个表面积涂满了红色的正方体,在它的面上等距离的横竖各切两刀,共得到27个相相同的小正方体。在这27个小正方体中,三面有红色、两面有红色、一面有红色以及各面都没有红色的小正方体各有_________个.
2、如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水多少升?
【真题链接】
1、(2020年西大附中)一个棱长为7厘米的小正方形,需要_____块这样的小正方形才能拼成体积为2744m 的正方体。
2、(2021年西大附中)一个圆柱形容器里面装有一半的水,恰好是120毫升,若把这个圆柱形容器里面的水倒入一个与它等底等高的圆锥形容器里面,可溢出_______毫升.
3、(2021年西大附中)把一根长1.5米的圆柱木料锯成三段小圆柱,表面积增加80平方分米,这根木料的体积是________立方米.
4、(2020年西大附中)四个同样大小的圆柱形拼成一个高为40厘米的大圆柱时,表面积减少了72平方厘米,则原来每个小圆柱的体积是________立方厘米 .
5、(2020新民)把一个长是5厘米,宽和高都是3厘米的长方题截成两块,其中一块是棱长是3厘米的正方体,则另一块的体积是_________
6、(2021年海安县)流动的水:有圆柱体、长方体和正方体玻璃容器连在一起,容器下面用细管连接起来,水可以流动,并装有A、B两个阀门.已知圆柱体底面积为25平方厘米,水深14厘米,长方体底面积为15平方厘米,水深10厘米,正方体底面积10平方厘米,无水.
(1)如果打开A阀,等水停止流动,此时长方体水深多少厘米?
(2)接着打开B阀,等水停止流动,此时正方体水深多少厘米?
课堂小测(15分钟)
1、一个长方体的棱长总和是72分米,长、宽、高的比为4:3:2,求长方体的体积是_________.
2、长方体的长扩大2倍,宽增加一倍,高扩大成原来的3倍,求所得长方体体积是原来的 ________倍。
3、一个长方体的高增加5米后变成一个正方体,表面积增加160平方米,原来长方体的体积是_________.
4、用4个棱长为1厘米的小正方体拼一个长方体,长方体体积是___________立方厘米,表面积是________平方厘米.
5、一个圆柱的体积是60立方厘米,与它等底等高的圆锥体的体积是 立方厘米。如果这个圆锥的高为3厘米,那么圆柱的高是 厘米。
6、一个从里面量长8分米、宽5分米的长方体玻璃缸,里面装有水,水深20厘米.现在往玻璃缸里放入一个钢块,水面上升了2厘米.求这个钢块的体积是多少?
7、把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为____________
作业1
1、填空题
1.一个九位数,最高位上是最大的一位数,千万位上是6,万位上是最小的合数,百位数上是最小的质数,十位上是自然数的单位,其余的都是最小的自然数,这个数写作________,改写成以万位作单位为___________,省略亿位后面的尾数是__________.
2.有五个数排成一排,它们的平均数是54,前三个数的平均数是49,后三个数的平均数是51,则第三个数是_______.
3.一个长方形的周长是42厘米,它的长比宽少25%,这个长方形的面积是_______.
4.规定x◎y=3x-2y,x◎(4◎1)=7,则x=____________.
5.已知长方体的棱长总和为36厘米,长、宽、高之比为4:3:2,长方体的体积是 ,表面积是 .
6.一个长方体,长与宽之比为2:1,宽与高之比为3:2,长方体全部棱长之和是220厘米,长方体的体积是 .
7.把3个棱长为10分米的正方体拼成一个长方体,表面积会减少 平方厘米.
8.正方体的棱长减少,它的表面积减少 .
9.等底等高的圆柱和圆锥,它们的体积相差12.56立方米,圆锥的体积是_____立方米 .
10.把一个长方体的长减少2厘米,就成为一个正方体,表面积比原来减少了80平方厘米,原来长方体表面积是_________平方厘米,体积是________立方厘米。
2、计算题
1、 2、
3、 4、
3、解答题
1、如图,(单位:dm)是一块零件的铜铸毛坯,每立方分米铜重8.9千克,这块零件铸铁毛坯的重量是多少吨?
2、一个圆柱的铁皮油桶装了半桶汽油,将汽油倒出60%后还剩25.12升。油桶的底面积是是12.56平方分米,油桶的高是多少?做这样的铁皮油桶(无盖)至少要多少铁皮?
3、如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?
4、在一个长25cm,宽12cm,高20cm的长方体玻璃缸中装入一个棱长8cm的正方体铅块,然后往缸中放一些水,使它完全淹没这个正方体铅块,当铅块从缸中取出时,缸中的水会下降多少厘米?
三、解答题
1、 一个长20厘米、宽10厘米、高20厘米的无盖长方体玻璃容器,里面盛有一些红色溶液.小明想知道溶液的深,他将一根底面边长5厘米,长1米的长方体木条垂直插入到容器底部,取出后量得木条被染红的部分长16厘米.原来容器内红色溶液深多少厘米?
2、如图,在棱长为3的正方体中由上到下,由左到右,由前到后,有三个底面积是1的正方形高为3的长方体的洞,则所得物体的表面积为 .
3、牙膏出口处是直径是4毫米的圆形,小红每次刷牙都挤出1厘米牙膏。这样,一支牙膏可用36次。该品牌的牙膏推出的新包装只是将出口处直径改为6毫米,小红还是按习惯挤出1厘米长的牙膏。这样,这一支牙膏可以用多少次
4、有一个棱长为4厘米的正方体橡皮泥.
(1)求这个正方体橡皮泥的表面积;
(2)在正方体橡皮泥上面正中向下挖一个棱长为2厘米的正方体小洞,接着在小洞的底面正中再向下挖一个棱长为1厘米的正方体小洞,最终剩下的橡皮泥如右图所示.若橡皮泥每立方厘米约重4克,则最终剩下的橡皮泥约有多少克?
(3)求第二问中最终剩下的橡皮泥的表面积.
《立体图形》答案
【变式训练1】答案:1、1296立方厘米,792平方厘米
2、48立方厘米,88平方厘米
3、480立方厘米,376平方厘米
【变式训练2】答案:1、3:10 2、25 3、4:3
【变式训练3】答案:1、9 2、60立方厘米 3、24平方厘米
【变式训练4】答案:1、34平方厘米 2、120 3、
【变式训练5】答案:1、44 2、194 3、26.69
【变式训练6】答案:1、 245 2、396 3、148
【变式训练7】答案:1、4000 2、188.4
【变式训练8】答案:1、600 2、16或24 3、125.6
【变式训练9】答案:1、400,3000 2、56平方厘米 3、1774平方厘米,1422平方厘米
【变式训练10】答案:1、450立方厘米 2、450立方厘米 3、5厘米
【变式训练11】答案:1、7分米 2、3.2厘米 3、3厘米,9厘米
【变式训练12】答案:1、12,36 2、157,443 3、159.48立方厘米
【拓展提高】答案:1、26 2、400升
【课程目标】
1、掌握立体图形切割拼补后表面积和体积的变化
2、掌握运用等积法求不规则图形的体积
3、培养学生的空间思维能力及细心习惯
知识点一:按比例分配
【例1】已知长方体的棱长总和为36厘米,长、宽、高之比为4:3:2,求这个长方体的体积和表面积。
【变式训练1】
1、一个长方体的长、宽、高的比是3:2:1,已知长方体的棱长总和是144厘米,它的体积是 .表面积是 .
2、已知长方体的长是宽的2倍,高是宽的3倍,棱长总和为48厘米,这个长方体的体积是_________,表面积是__________。
3、一个长方体棱长总和是96厘米,长比宽多25%,高比宽少,这个长方体的体积是_________,表面积是__________。
知识点二:立体图形和比的应用
【例2】甲、乙两个圆柱体底面半径的比是2:3,体积比是5:6,甲、乙两个圆柱高的比是 .
【变式训练2】
1、一个圆柱体和一个圆锥体,半径之比是1:2,高之比是2:5,它们体积之比为 .
2、有两个底面半径相等的圆柱和圆锥,高的比是4:5,圆柱的体积是60立方厘米,则圆锥的体积是______立方厘米。
3、圆柱体和圆锥体的底面半径的比是2:3,则圆柱与圆锥的体积比是16:9,求圆柱的高和圆锥的高的比是______:_________.
知识点三:表面积和体积的变化
【例3】一个长方体,如果它的长和宽都扩大4倍,高变为原来的,那么这个长方体的体积扩大 倍.
【变式训练3】
1、长方体的长和宽都增加3倍,高不变,则它的体积变为原来的_______倍
2、长方体的长为5cm,宽为4cm,高为3cm,将长方体的长增加,宽减少,高扩大两倍,求所得长方形的体积比原来的多_______.
3、一个圆锥,增加后的高与原来的高的比是8:3.如果圆锥的体积不变,原来的底面积比现在的底面积大40cm2.现在的底面积是__________.
【例4】如图,长方体的长20厘米,宽10厘米,高5厘米.在长方体的一角去掉一个棱长5厘米的正方体.求剩下部分的表面积是多少?
【变式训练4】
1、图是一个长3厘米、宽与高都是2厘米的长方体。将它挖掉一个棱长1厘米的小正方体,它的表面积________。
2、一个棱长为4分米的正方体,分别在前后、左右、上下各面的中心位置,挖去一个棱长为1分米的小正方体,挖完后得到的正方体,它的表面积是________平方分米。
3、下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为厘米,那么最后得到的立体图形的表面积是多少平方厘米?
【例5】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.
【变式训练5】
1、用棱长是1厘米的立方块拼成如图所示的立体图形,问该图形的表面积是多少平方厘米
2、如图,棱长分别为1厘米,2厘米,3厘米,5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是 平方厘米.
3、将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.这个物体的表面积是 平方米.(π=3.14)
【例6】一个长方体,如果高增加3厘米,就成为一个正方体.这时表面积比原来增加了96平方厘米。原来的长方体的体积是多少立方厘米?
【变式训练6】
1、一个长方体,如宽增加2厘米,就成了正方体,而且表面积增加56平方厘米,原来这个长方体的体积是______立方厘米。
2、一个长方体木块,从中间截去高为5厘米长方体后,合并后便成为一个正方体,表面积减少了120平方厘米,原长方体的体积是__________立方厘米.
3、一个长方体,如果长增加2厘米,则体积增加40立方厘米,如果宽增加3厘米,则体积增加90立方厘米,如果高增加4厘米,则体积增加96立方厘米,原长方体的表面积是___________平方厘米.
【例7】如右图所示,这根石柱子的体积是 立方米.
答案:如图,假设再有一个一模一样的立体图形,即可拼接成一个高为28cm的圆柱体,求出圆柱体体积再除以2即可.
【变式训练7】
1、计算下面图形的体积
2、如图1是三个直立于水平面上的形状完全相同的几何体(下底面为圆面,单位:厘米).将它们拼成如图2的新几何体,则该新几何体的体积应为 立方厘米.
知识点四:切割、拼补立体图形
【例8】把2.4米长的长方体木料,平均锯成3段,表面积比原来增加了4.8平方分米,原来这根木料的体积是多少立方分米?
【变式训练8】
1、把一根长1 米的木料平均截成4段后,表面积增加了36平方厘米,原来这根木料的体积是 .
2、一个正方体体积是8dm3,把它平均分成4个长方体.表面积增加 dm2.
3、如图,一段圆柱形木料,如果截成两个小圆柱,它的表面积将增加6.28平方厘米,如果沿直径截成两个半圆柱,它的表面积将增加80平方厘米,求原圆柱的体积。
【例9】把3个棱长4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是 cm2.
【变式训练9】
1、把3个棱长为10分米的正方体拼成一个长方体,表面积会减少 平方厘米,长方体的体积是 立方厘米。
2、把3个正方体木块粘合成一个长方体,这个长方体的表面积会减少16cm2,求原正方体体积是 .
3、用3个相同的长方体木料拼成一个大长方体,每根的长是15厘米,宽是11厘米,高是7厘米.怎样拼才能使得拼成的长方体的表面积最大?最少是多少平方厘米?
知识点五:等积法
【例10】如图,一个长方体玻璃容器,从里面量长为3分米,宽为3分米,高4分米。向容器中倒入18升水,再把一个苹果放入水中,这时测得容器内的水面的高度是21厘米。这个苹果的体积是多少?
【变式训练10】
1、一个底面积1.5平方分米的玻璃缸里有一块石头,如图所示.水深18厘米,拿出石块后水面下降到15厘米,这块石头体积是多少?
2、有一种饮料瓶,如图所示,瓶身呈圆柱形,容积是600毫升。现在瓶中装有一些饮料,正放时饮料髙度为12厘米,倒放时空余部分的高度为4厘米。问:瓶内现有饮料多少立方厘米?
3、一个长方体玻璃杯中盛有水,水的高度是2.5厘米,玻璃杯内侧的底面积是72平方厘米,在这个杯中放进一个6厘米的正方体铁块后,铁块没有完全浸没,求这时水的高度是多少?
【例11】 棱长是6分米的正方体容器装满水,把容器里的水全部倒入一个长方体水箱,水箱从里面量长6分米,宽5分米,高8.5分米,这时倒入水箱里面的水深是多少分米?再要注满水箱应倒入多少升水?
【变式训练11】
1、一个棱长8分米的正方体水槽里装了490升水,把这些水倒入一个长10分米,宽7分米,高8分米的长方体水槽里,水槽里的水深是多少?
2、一个底面积为40cm,高6cm的圆锥体容器,装满水后全部倒入一个棱长为5cm的正方体容器里,水深多少厘米?
3、在甲箱中装入水,深度为15厘米,放进一个长10厘米宽9厘米,高5厘米的小正方体A,则水升高多少厘米? 若将这些水和物体A一起倒入乙箱,水深为多少厘米
知识点六:圆柱圆锥
【例12】等底等高的圆柱和圆锥,它们的体积之和是48立方厘米,则这个圆柱的体积是 立方厘米,圆锥的体积是 立方厘米.
【变式训练12】
1、一个圆柱和一个圆锥等底等高,它们的体积之差是24dm3,那么圆锥的体积是 dm3,圆柱的体积是 m3。
2、一个长方体木料,横截面是边长10厘米的正方形。从这根木料上截下6厘米长的一段,切削成一个最大的圆锥,圆锥的体积是 立方厘米,削去部分体积是 立方厘米。
3、下图为一个棱长6厘米的正方体,从正方体的底面向内挖一个最大的圆锥,剩下的体积是多少立方厘米?
【拓展提高】
1、有一个表面积涂满了红色的正方体,在它的面上等距离的横竖各切两刀,共得到27个相相同的小正方体。在这27个小正方体中,三面有红色、两面有红色、一面有红色以及各面都没有红色的小正方体各有_________个.
2、如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水多少升?
【真题链接】
1、(2020年西大附中)一个棱长为7厘米的小正方形,需要_____块这样的小正方形才能拼成体积为2744m 的正方体。
2、(2021年西大附中)一个圆柱形容器里面装有一半的水,恰好是120毫升,若把这个圆柱形容器里面的水倒入一个与它等底等高的圆锥形容器里面,可溢出_______毫升.
3、(2021年西大附中)把一根长1.5米的圆柱木料锯成三段小圆柱,表面积增加80平方分米,这根木料的体积是________立方米.
4、(2020年西大附中)四个同样大小的圆柱形拼成一个高为40厘米的大圆柱时,表面积减少了72平方厘米,则原来每个小圆柱的体积是________立方厘米 .
5、(2020新民)把一个长是5厘米,宽和高都是3厘米的长方题截成两块,其中一块是棱长是3厘米的正方体,则另一块的体积是_________
6、(2021年海安县)流动的水:有圆柱体、长方体和正方体玻璃容器连在一起,容器下面用细管连接起来,水可以流动,并装有A、B两个阀门.已知圆柱体底面积为25平方厘米,水深14厘米,长方体底面积为15平方厘米,水深10厘米,正方体底面积10平方厘米,无水.
(1)如果打开A阀,等水停止流动,此时长方体水深多少厘米?
(2)接着打开B阀,等水停止流动,此时正方体水深多少厘米?
课堂小测(15分钟)
1、一个长方体的棱长总和是72分米,长、宽、高的比为4:3:2,求长方体的体积是_________.
2、长方体的长扩大2倍,宽增加一倍,高扩大成原来的3倍,求所得长方体体积是原来的 ________倍。
3、一个长方体的高增加5米后变成一个正方体,表面积增加160平方米,原来长方体的体积是_________.
4、用4个棱长为1厘米的小正方体拼一个长方体,长方体体积是___________立方厘米,表面积是________平方厘米.
5、一个圆柱的体积是60立方厘米,与它等底等高的圆锥体的体积是 立方厘米。如果这个圆锥的高为3厘米,那么圆柱的高是 厘米。
6、一个从里面量长8分米、宽5分米的长方体玻璃缸,里面装有水,水深20厘米.现在往玻璃缸里放入一个钢块,水面上升了2厘米.求这个钢块的体积是多少?
7、把14个棱长为1的正方体,在地面上堆叠成如图所示的立体,然后将露出的表面部分涂成红色,那么红色部分的面积为____________
作业1
1、填空题
1.一个九位数,最高位上是最大的一位数,千万位上是6,万位上是最小的合数,百位数上是最小的质数,十位上是自然数的单位,其余的都是最小的自然数,这个数写作________,改写成以万位作单位为___________,省略亿位后面的尾数是__________.
2.有五个数排成一排,它们的平均数是54,前三个数的平均数是49,后三个数的平均数是51,则第三个数是_______.
3.一个长方形的周长是42厘米,它的长比宽少25%,这个长方形的面积是_______.
4.规定x◎y=3x-2y,x◎(4◎1)=7,则x=____________.
5.已知长方体的棱长总和为36厘米,长、宽、高之比为4:3:2,长方体的体积是 ,表面积是 .
6.一个长方体,长与宽之比为2:1,宽与高之比为3:2,长方体全部棱长之和是220厘米,长方体的体积是 .
7.把3个棱长为10分米的正方体拼成一个长方体,表面积会减少 平方厘米.
8.正方体的棱长减少,它的表面积减少 .
9.等底等高的圆柱和圆锥,它们的体积相差12.56立方米,圆锥的体积是_____立方米 .
10.把一个长方体的长减少2厘米,就成为一个正方体,表面积比原来减少了80平方厘米,原来长方体表面积是_________平方厘米,体积是________立方厘米。
2、计算题
1、 2、
3、 4、
3、解答题
1、如图,(单位:dm)是一块零件的铜铸毛坯,每立方分米铜重8.9千克,这块零件铸铁毛坯的重量是多少吨?
2、一个圆柱的铁皮油桶装了半桶汽油,将汽油倒出60%后还剩25.12升。油桶的底面积是是12.56平方分米,油桶的高是多少?做这样的铁皮油桶(无盖)至少要多少铁皮?
3、如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?
4、在一个长25cm,宽12cm,高20cm的长方体玻璃缸中装入一个棱长8cm的正方体铅块,然后往缸中放一些水,使它完全淹没这个正方体铅块,当铅块从缸中取出时,缸中的水会下降多少厘米?
三、解答题
1、 一个长20厘米、宽10厘米、高20厘米的无盖长方体玻璃容器,里面盛有一些红色溶液.小明想知道溶液的深,他将一根底面边长5厘米,长1米的长方体木条垂直插入到容器底部,取出后量得木条被染红的部分长16厘米.原来容器内红色溶液深多少厘米?
2、如图,在棱长为3的正方体中由上到下,由左到右,由前到后,有三个底面积是1的正方形高为3的长方体的洞,则所得物体的表面积为 .
3、牙膏出口处是直径是4毫米的圆形,小红每次刷牙都挤出1厘米牙膏。这样,一支牙膏可用36次。该品牌的牙膏推出的新包装只是将出口处直径改为6毫米,小红还是按习惯挤出1厘米长的牙膏。这样,这一支牙膏可以用多少次
4、有一个棱长为4厘米的正方体橡皮泥.
(1)求这个正方体橡皮泥的表面积;
(2)在正方体橡皮泥上面正中向下挖一个棱长为2厘米的正方体小洞,接着在小洞的底面正中再向下挖一个棱长为1厘米的正方体小洞,最终剩下的橡皮泥如右图所示.若橡皮泥每立方厘米约重4克,则最终剩下的橡皮泥约有多少克?
(3)求第二问中最终剩下的橡皮泥的表面积.
《立体图形》答案
【变式训练1】答案:1、1296立方厘米,792平方厘米
2、48立方厘米,88平方厘米
3、480立方厘米,376平方厘米
【变式训练2】答案:1、3:10 2、25 3、4:3
【变式训练3】答案:1、9 2、60立方厘米 3、24平方厘米
【变式训练4】答案:1、34平方厘米 2、120 3、
【变式训练5】答案:1、44 2、194 3、26.69
【变式训练6】答案:1、 245 2、396 3、148
【变式训练7】答案:1、4000 2、188.4
【变式训练8】答案:1、600 2、16或24 3、125.6
【变式训练9】答案:1、400,3000 2、56平方厘米 3、1774平方厘米,1422平方厘米
【变式训练10】答案:1、450立方厘米 2、450立方厘米 3、5厘米
【变式训练11】答案:1、7分米 2、3.2厘米 3、3厘米,9厘米
【变式训练12】答案:1、12,36 2、157,443 3、159.48立方厘米
【拓展提高】答案:1、26 2、400升
同课章节目录
