2021-2022学年人教版九年级数学下册第二十七章相似复习 练习题
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十七章相似复习 练习题 |

|
|
| 格式 | docx | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览


文档简介
第二十七章 相似
一、单项选择题
1.已知:线段a=5cm,b=2cm,则=( )
A. B.4 C. D.
2.把mn=pq(mn≠0)写成比例式,写错的是( )
A. B. C. D.
3. 下列结论不正确的是( )
A.有一个锐角相等的两个直角三角形相似
B.有一个锐角相等的两个等腰三角形相似
C.有一个角等于120°的两个等腰三角形相似
D.有一个角为60°的两个等腰三角形相似
4.如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若=,DE=4,则EF的长是( )
A. B. C.6 D.10
5.若△ABC和△DEF满足下列条件,其中使△ABC与△DEF相似的是( )
A.AB=3,BC=6,AC=9;DE=2,EF=4,DF=6
B.AB=4,BC=6,AC=8;DE=5,EF=10,DF=15
C.AB=1,BC=,AC=2;DE=,EF=,DF=
D.AB=1,BC=,AC=3;DE=,EF=2,DF=
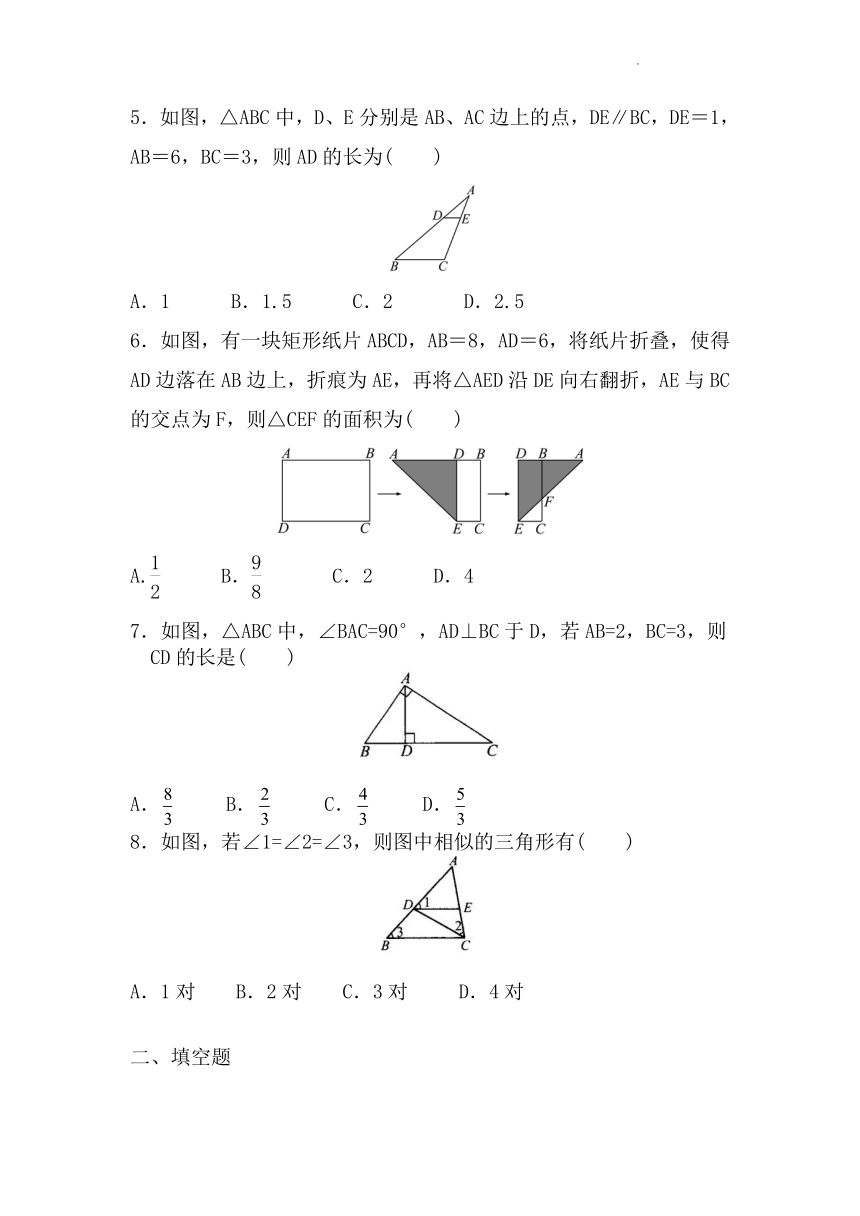
5.如图,△ABC中,D、E分别是AB、AC边上的点,DE∥BC,DE=1,AB=6,BC=3,则AD的长为( )
A.1 B.1.5 C.2 D.2.5
6.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )
A. B. C.2 D.4
7.如图,△ABC中,∠BAC=90°,AD⊥BC于D,若AB=2,BC=3,则CD的长是( )
A. B. C. D.
8.如图,若∠1=∠2=∠3,则图中相似的三角形有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
9.若(abc≠0),则=_________.
10.已知△ABC∽△A′B′C′,相似比为3∶4,△ABC的周长为6,则△A′B′C′的周长为 .
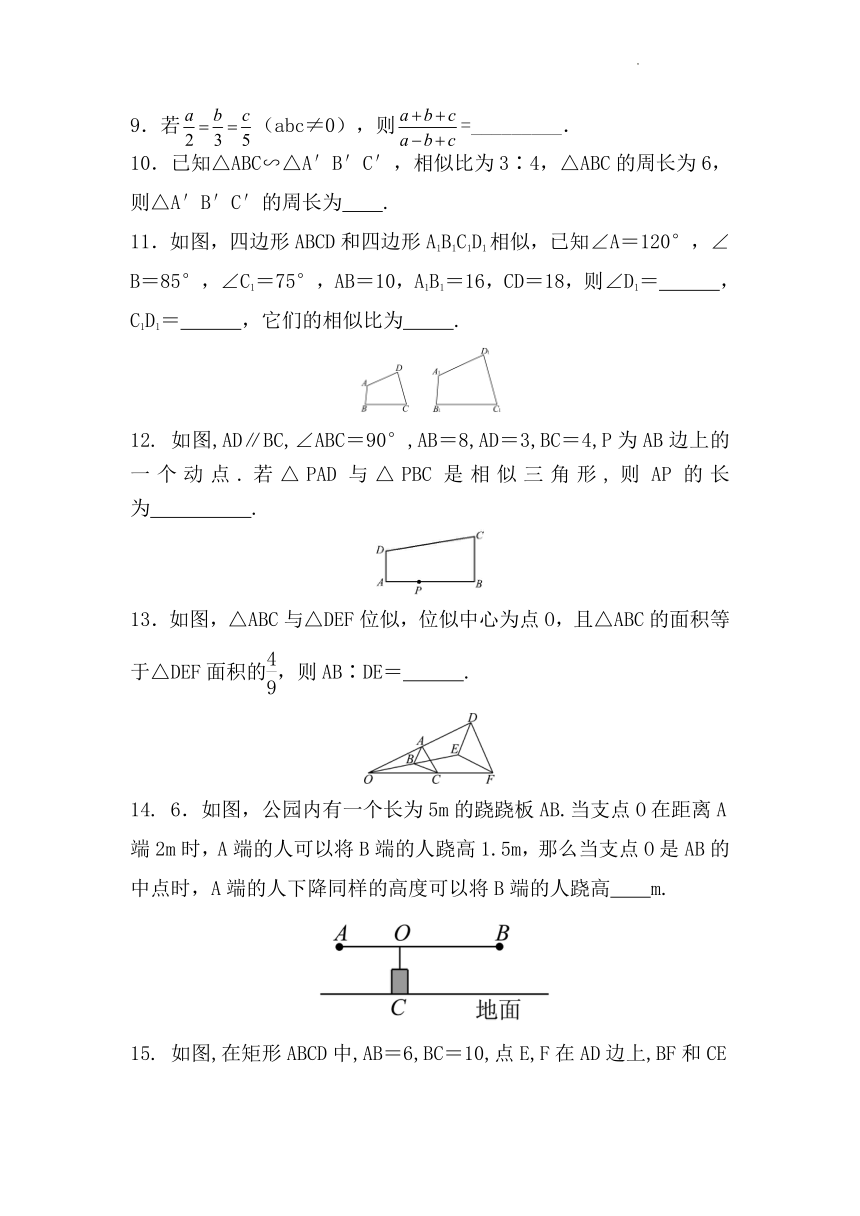
11.如图,四边形ABCD和四边形A1B1C1D1相似,已知∠A=120°,∠B=85°,∠C1=75°,AB=10,A1B1=16,CD=18,则∠D1= ,C1D1= ,它们的相似比为 .
12. 如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,P为AB边上的一个动点.若△PAD与△PBC是相似三角形,则AP的长为 .
13.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB∶DE= .
14. 6.如图,公园内有一个长为5m的跷跷板AB.当支点O在距离A端2m时,A端的人可以将B端的人跷高1.5m,那么当支点O是AB的中点时,A端的人下降同样的高度可以将B端的人跷高 m.
15. 如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为 .
三、解答题
16. 如图,四边形ABCD∽四边形A'B'C'D',求边x,y的长度和角α的大小.
17.如图,在平行四边形ABCD中,E为BC边上的一点.连接AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF∶FA的值.
18. 如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
19.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.
20.(1)如图①,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC=90°.求证:△ADE∽△BEC;
(2)一位同学在尝试了上题后还发现:如图②,图③,只要A、E、B三点在同一直线上,且∠A=∠B=∠DEC,则(1)中结论总成立.你同意吗?请选择其中之一说明理由.
答案:
一、
1-8 CDBCA CDD
二、
9.
10. 8
11. 80° 28.8
12. 或2或6
13. 2∶3
14. 1
15. 35
三、
16. 解:∵四边形ABCD∽四边形A'B'C'D',
∴,∠C=α,∠D=∠D'=140°.
∴x=12,y=,α=∠C=360°-∠A-∠B-∠D=360°-62°-75°-140°=83°.
17. 解:(1)∵四边形ABCD为平行四边形,∴∠B=∠D,AD∥BC,∴∠AEB=∠EAD.又∵AE=AB,∴∠B=∠AEB.∴∠B=∠EAD,∠EAD=∠D;
(2)∵AD∥BC,∴∠FAD=∠FEB,∠ADF=∠EBF,∴△ADF∽△EBF,EF∶FA=BE∶AD=BE∶BC=1∶2.
18. 解:(1)在Rt△ABC中,∵∠ACB=90°,AB=6,BC=6,
∴AC==12,∴AE=AC-CE=9.
∵AB∥CD,∴△CDE∽△ABE,
∴.
(2)在Rt△BCE中,∵∠ECB=90°,CE=3,BC=6,
∴BE=.
∴由(1)知△CDE∽△ABE,∴,
∴DE=.
∵.
∵∠D=∠D,∴△CDE∽△BDC.
19. 证明:(1)∵
∴
又 ∠ACB=∠DCE=90°,
∴ △ACB∽△DCE.
(2)∵ △ACB∽△DCE,∴ ∠ABC=∠DEC.
又 ∠ABC+∠A =90°,∴ ∠DEC+∠A=90°.
∴ ∠EFA=90°. ∴ EF⊥AB.
20. 解:(1)∵∠A=∠B=∠DEC=90°,∴∠DEA+∠CEB=90°,∠DEA+∠D=90°,∴∠D=∠CEB,∴△ADE∽△BEC;
(2)同意.以题图②为例说明:∵∠A=∠B=∠DEC,∠A+∠D=∠DEC+∠CEB,∴∠D=∠CEB,∴△ADE∽△BEC.
一、单项选择题
1.已知:线段a=5cm,b=2cm,则=( )
A. B.4 C. D.
2.把mn=pq(mn≠0)写成比例式,写错的是( )
A. B. C. D.
3. 下列结论不正确的是( )
A.有一个锐角相等的两个直角三角形相似
B.有一个锐角相等的两个等腰三角形相似
C.有一个角等于120°的两个等腰三角形相似
D.有一个角为60°的两个等腰三角形相似
4.如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若=,DE=4,则EF的长是( )
A. B. C.6 D.10
5.若△ABC和△DEF满足下列条件,其中使△ABC与△DEF相似的是( )
A.AB=3,BC=6,AC=9;DE=2,EF=4,DF=6
B.AB=4,BC=6,AC=8;DE=5,EF=10,DF=15
C.AB=1,BC=,AC=2;DE=,EF=,DF=
D.AB=1,BC=,AC=3;DE=,EF=2,DF=
5.如图,△ABC中,D、E分别是AB、AC边上的点,DE∥BC,DE=1,AB=6,BC=3,则AD的长为( )
A.1 B.1.5 C.2 D.2.5
6.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )
A. B. C.2 D.4
7.如图,△ABC中,∠BAC=90°,AD⊥BC于D,若AB=2,BC=3,则CD的长是( )
A. B. C. D.
8.如图,若∠1=∠2=∠3,则图中相似的三角形有( )
A.1对 B.2对 C.3对 D.4对
二、填空题
9.若(abc≠0),则=_________.
10.已知△ABC∽△A′B′C′,相似比为3∶4,△ABC的周长为6,则△A′B′C′的周长为 .
11.如图,四边形ABCD和四边形A1B1C1D1相似,已知∠A=120°,∠B=85°,∠C1=75°,AB=10,A1B1=16,CD=18,则∠D1= ,C1D1= ,它们的相似比为 .
12. 如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,P为AB边上的一个动点.若△PAD与△PBC是相似三角形,则AP的长为 .
13.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB∶DE= .
14. 6.如图,公园内有一个长为5m的跷跷板AB.当支点O在距离A端2m时,A端的人可以将B端的人跷高1.5m,那么当支点O是AB的中点时,A端的人下降同样的高度可以将B端的人跷高 m.
15. 如图,在矩形ABCD中,AB=6,BC=10,点E,F在AD边上,BF和CE交于点G,若EF=AD,则图中阴影部分的面积为 .
三、解答题
16. 如图,四边形ABCD∽四边形A'B'C'D',求边x,y的长度和角α的大小.
17.如图,在平行四边形ABCD中,E为BC边上的一点.连接AE.
(1)若AB=AE,求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF∶FA的值.
18. 如图,AB∥CD,AC与BD交于点E,且∠ACB=90°,AB=6,BC=6,CE=3.
(1)求CD的长;
(2)求证:△CDE∽△BDC.
19.如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.
20.(1)如图①,已知A、E、B三点在同一直线上,且∠A=∠B=∠DEC=90°.求证:△ADE∽△BEC;
(2)一位同学在尝试了上题后还发现:如图②,图③,只要A、E、B三点在同一直线上,且∠A=∠B=∠DEC,则(1)中结论总成立.你同意吗?请选择其中之一说明理由.
答案:
一、
1-8 CDBCA CDD
二、
9.
10. 8
11. 80° 28.8
12. 或2或6
13. 2∶3
14. 1
15. 35
三、
16. 解:∵四边形ABCD∽四边形A'B'C'D',
∴,∠C=α,∠D=∠D'=140°.
∴x=12,y=,α=∠C=360°-∠A-∠B-∠D=360°-62°-75°-140°=83°.
17. 解:(1)∵四边形ABCD为平行四边形,∴∠B=∠D,AD∥BC,∴∠AEB=∠EAD.又∵AE=AB,∴∠B=∠AEB.∴∠B=∠EAD,∠EAD=∠D;
(2)∵AD∥BC,∴∠FAD=∠FEB,∠ADF=∠EBF,∴△ADF∽△EBF,EF∶FA=BE∶AD=BE∶BC=1∶2.
18. 解:(1)在Rt△ABC中,∵∠ACB=90°,AB=6,BC=6,
∴AC==12,∴AE=AC-CE=9.
∵AB∥CD,∴△CDE∽△ABE,
∴.
(2)在Rt△BCE中,∵∠ECB=90°,CE=3,BC=6,
∴BE=.
∴由(1)知△CDE∽△ABE,∴,
∴DE=.
∵.
∵∠D=∠D,∴△CDE∽△BDC.
19. 证明:(1)∵
∴
又 ∠ACB=∠DCE=90°,
∴ △ACB∽△DCE.
(2)∵ △ACB∽△DCE,∴ ∠ABC=∠DEC.
又 ∠ABC+∠A =90°,∴ ∠DEC+∠A=90°.
∴ ∠EFA=90°. ∴ EF⊥AB.
20. 解:(1)∵∠A=∠B=∠DEC=90°,∴∠DEA+∠CEB=90°,∠DEA+∠D=90°,∴∠D=∠CEB,∴△ADE∽△BEC;
(2)同意.以题图②为例说明:∵∠A=∠B=∠DEC,∠A+∠D=∠DEC+∠CEB,∴∠D=∠CEB,∴△ADE∽△BEC.
