小升初必考专题:加乘原理(讲义)2020-2021学年数学六年级下册(含答案)全国通用
文档属性
| 名称 | 小升初必考专题:加乘原理(讲义)2020-2021学年数学六年级下册(含答案)全国通用 |

|
|
| 格式 | docx | ||
| 文件大小 | 27.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 10:45:36 | ||
图片预览

文档简介
(
加乘原理
)
(
知识要点
)
一、乘法原理:
一般地,如果完成一件事需要n个步骤(缺一不可),
第1步有m1种不同的方法,
第2步有m2种不同的方法,
第3步有m3种不同的方法,……,
第n步有mn种不同的方法,
则完成这件事一共有N=m1×m2×m3×…×mn种不同的方法。
二、加法原理:
一般地,如果完成一件事有n类方法(每一类中的任何一种方法都能独立完成这件事情),
第1类有m1种不同的方法,
第2类有m2种不同的方法,
第3类有m3种不同的方法,……,
第n类有mn种不同的方法,
则完成这件事一共有N=m1+m2+m3+…+mn种不同的方法。
八字要诀:“加法分类,类类独立”。
“乘法分步,步步相关”。
培养目标:
综合运用乘法原理和加法原理。
在分步分析中结合分类讨论,在分类讨论中结合分步分析;明确哪些是分步,哪些是分类。
了解与加、乘原理的常见题型:数论类问题、染色问题、图形组合。
(
例
1
一辆肇事车辆撞人后逃离现场,警察到现场调查取证,目击者只能记得车牌号是由
1
,
4
,
6
,
7
,
8
五个数字组成,却把它们的排列顺序忘记了。如果在电脑中随机的输入一个由这五个数字构成的车牌号,那么,输入的车牌号正好是肇事车辆车牌号的可能性是
( )(
填几分之一
)
。
)
(
例
2
袋中有
3
个红球,
4
个黄球和
5
个白球,小明从中任意拿出
6
个球,他拿出球的情况共有
_____
种可能。
)
(
例
3
一个七位数,其数码只能是
2
或
3
,且没有两个
3
是相邻的。请问这样的七位数共有多少个?
)
(
例
4
用
0
~
5
这六个数字可组成
_____
个没有重复数字的四位偶数。
) (
例
5
如图所示,地图上有
A
、
B
、
C
、
D
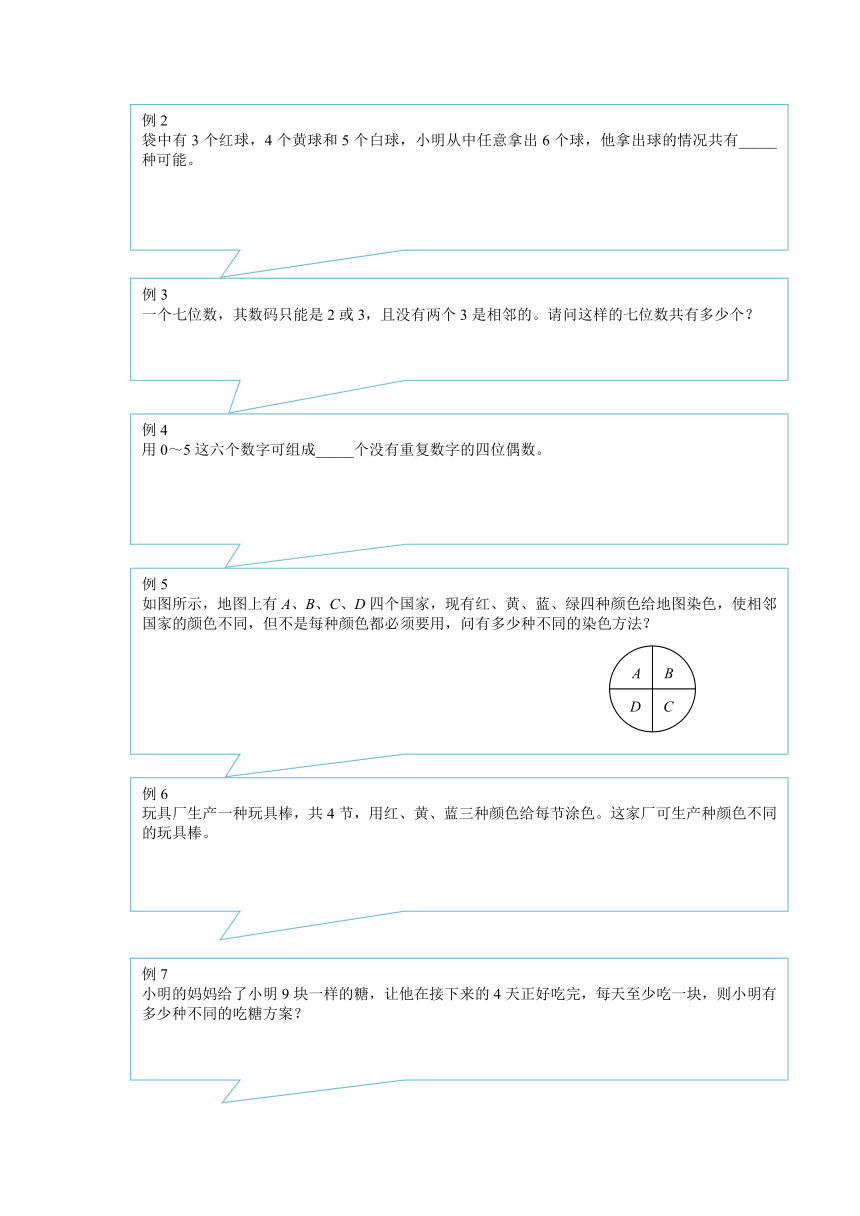
四个国家,现有红、黄、蓝、绿四种颜色给地图染色,使相邻国家的颜色不同,但不是每种颜色都必须要用,问有多少种不同的染色方法?
)
(
例
6
玩具厂生产一种玩具棒,共
4
节,用红、黄、蓝三种颜色给每节涂色。这家厂可生产种颜色不同的玩具棒。
)
(
例
7
小明的妈妈给了小明
9
块一样的糖,让他在接下来的
4
天正好吃完,每天至少吃一块,则小明有多少种不同的吃糖方案?
)
测试题
1.大林和小林共有小人书不超过9本,他们各自有小人书的数目有多少种可能的情况?
2.有三个不完全一样的正方体,每个正方体的六个面上分别标有数字1、2、3、4、5、6。将三个正方体放到桌面上,向上的一面数字之和为奇数的有多少种情形?
3.用1、2、3、4、5五个数字,不许重复,位数不限,能写出多少个3的倍数?
4.用数码1,2,3,4,组成的没有重复数字的四位数中能被11整除的数有( )个。
5.有一批规格相同的圆棒,每根划分成长度相同的
五节,每节用红、黄、蓝三种颜色来涂。问:可以得到多少种颜色不同的圆棒?
6.某工作需要钳工2人和电工2人共同完成,现有钳工A、B、C,电工D、E、F,另有G钳工、电工都会。从这7个人中挑选若干人去完成这项工作,共有_____不同选法。
7.学校广播台要在四年级6个班中招收8名广播员,每个班至少1名,共有_____种不同的招收方法。
答案
1.【分析】
按大林和小林共有小人书的本书分10类:
第1类:大林和小林共有9本的话,有10种可能;
第2类:大林和小林共有8本的话,有9种可能;
第3类:大林和小林共有7本的话,有8种可能;
第4类:大林和小林共有6本的话,有7种可能;
第5类:大林和小林共有5本的话,有6种可能;
第6类:大林和小林共有4本的话,有5种可能;
第7类:大林和小林共有3本的话,有4种可能;
第8类:大林和小林共有2本的话,有3种可能;
第9类:大林和小林共有1本的话,有2种可能;
第10类:大林和小林共有0本的话,有1种可能;
由加法原理,大林和小林各自有小人书的数目有10+9+8+7+6+5+4+3+2+1=55种可能的情
况。
2.【分析】
因为奇数+奇数+奇数=奇数、奇数+奇数+偶数=偶数、
奇数+偶数+偶数=奇数、偶数+偶数+偶数=偶数;
要使3个数字之和为奇数,则这3个数字为三个奇数或一奇两偶,
由于放三个正方体可认为是一个一个地放分2类考虑:
第1类,3个数字同为奇数,出现奇数为1、3、5,有3种可能;放第1、2、3个正方体时,各有3
种可能;
由乘法原理,3个数字同为奇数,共有3×3×3=27种不同的情形。
第2类,3个数字为一奇两偶,出现奇数为1、3、5,有3种可能;出现偶数为2、4、6,有3种可
能;放第1、2、3个正方体时,各有3种可能;出现奇数的正方体的顺序有3种情况;
由乘法原理,3个数字为一奇两偶,共有(3×3×3)×3=81种不同的情形。
由加法原理,3个正方体向上的一面数字之和为奇数的共有27+81=108种不同的情形。
3.【分析】
按照位数分5类考虑:
第1类,一位数为3、有1个;
第2类,两位数的数码为1、2或1、5或2、4或4、5,共4组,由乘法原理,每一组可以组成
2×1=2种情况,共有2×4=8个不同的两位数;
第3类,三位数的数码为1、2、3或1、3、5或2、3、4或3、4、5,共4组,由乘法原理,每一
组可以组成3×2×1=6种情况,共可以组成6×4=24个不同的三位数;
第4类,四位数的数码为1、2、4、5,由乘法原理,有4×3×2×1=24个不同的四位数;
第5类,五位数的数码为1、2、3、4、5,由乘法原理,有5×4×3×2×1=120个不同的五位数;
由加法原理,用1、2、3、4、5五个数字,不许重复,位数不限,能写出1+8+24+24+120=177
个3的倍数。
4.【分析】
略
5.【分析】
每节有3种颜色可选,由乘法原理有3×3×3×3×3=35=243种涂法;
其中有些圆棒顺着看和倒着看颜色不一样,却被计算了2次;
有些圆棒顺着看与倒着看颜色一样,这种情况的玩具棒没有被重复计算,
这样的圆棒关于中心对称,有 3×3×3=27种涂法;
可以得到(243-27)÷2+27=135或(243+27)÷2=135种颜色不同的圆棒。
6.【分析】
对G进行分类讨论:
当选G当钳工时,从A、B、C中再选出1个钳工,有3种选法;
从D、E、F中选出2个电工,考虑谁没有被选上,有3种选法;
由乘法原理有3×3=9种;
当选G当电工时,从A、B、C中选出2个钳工,考虑谁没有被选上,有3种选法;
从D、E、F中再选出1个电工,有3种选法;
由乘法原理有3×3=9种;
当不选G时,有3×3=9种;
从A、B、C中选出2个钳工,考虑谁没有被选上,有3种选法;
从D、E、F中选出2个电工,考虑谁没有被选上,有3种选法;
由乘法原理有3×3=9种;
由加法原理,从这7个人中挑选若干人去完成这项工作,共有9+9+9=27种。
7.【分析】
插板法:8名广播员有7个间隔,要分成6份,需要5个间隔,即有两个间隔不需要插板。
所以有7×6÷2=21种方案。
加乘原理
)
(
知识要点
)
一、乘法原理:
一般地,如果完成一件事需要n个步骤(缺一不可),
第1步有m1种不同的方法,
第2步有m2种不同的方法,
第3步有m3种不同的方法,……,
第n步有mn种不同的方法,
则完成这件事一共有N=m1×m2×m3×…×mn种不同的方法。
二、加法原理:
一般地,如果完成一件事有n类方法(每一类中的任何一种方法都能独立完成这件事情),
第1类有m1种不同的方法,
第2类有m2种不同的方法,
第3类有m3种不同的方法,……,
第n类有mn种不同的方法,
则完成这件事一共有N=m1+m2+m3+…+mn种不同的方法。
八字要诀:“加法分类,类类独立”。
“乘法分步,步步相关”。
培养目标:
综合运用乘法原理和加法原理。
在分步分析中结合分类讨论,在分类讨论中结合分步分析;明确哪些是分步,哪些是分类。
了解与加、乘原理的常见题型:数论类问题、染色问题、图形组合。
(
例
1
一辆肇事车辆撞人后逃离现场,警察到现场调查取证,目击者只能记得车牌号是由
1
,
4
,
6
,
7
,
8
五个数字组成,却把它们的排列顺序忘记了。如果在电脑中随机的输入一个由这五个数字构成的车牌号,那么,输入的车牌号正好是肇事车辆车牌号的可能性是
( )(
填几分之一
)
。
)
(
例
2
袋中有
3
个红球,
4
个黄球和
5
个白球,小明从中任意拿出
6
个球,他拿出球的情况共有
_____
种可能。
)
(
例
3
一个七位数,其数码只能是
2
或
3
,且没有两个
3
是相邻的。请问这样的七位数共有多少个?
)
(
例
4
用
0
~
5
这六个数字可组成
_____
个没有重复数字的四位偶数。
) (
例
5
如图所示,地图上有
A
、
B
、
C
、
D
四个国家,现有红、黄、蓝、绿四种颜色给地图染色,使相邻国家的颜色不同,但不是每种颜色都必须要用,问有多少种不同的染色方法?
)
(
例
6
玩具厂生产一种玩具棒,共
4
节,用红、黄、蓝三种颜色给每节涂色。这家厂可生产种颜色不同的玩具棒。
)
(
例
7
小明的妈妈给了小明
9
块一样的糖,让他在接下来的
4
天正好吃完,每天至少吃一块,则小明有多少种不同的吃糖方案?
)
测试题
1.大林和小林共有小人书不超过9本,他们各自有小人书的数目有多少种可能的情况?
2.有三个不完全一样的正方体,每个正方体的六个面上分别标有数字1、2、3、4、5、6。将三个正方体放到桌面上,向上的一面数字之和为奇数的有多少种情形?
3.用1、2、3、4、5五个数字,不许重复,位数不限,能写出多少个3的倍数?
4.用数码1,2,3,4,组成的没有重复数字的四位数中能被11整除的数有( )个。
5.有一批规格相同的圆棒,每根划分成长度相同的
五节,每节用红、黄、蓝三种颜色来涂。问:可以得到多少种颜色不同的圆棒?
6.某工作需要钳工2人和电工2人共同完成,现有钳工A、B、C,电工D、E、F,另有G钳工、电工都会。从这7个人中挑选若干人去完成这项工作,共有_____不同选法。
7.学校广播台要在四年级6个班中招收8名广播员,每个班至少1名,共有_____种不同的招收方法。
答案
1.【分析】
按大林和小林共有小人书的本书分10类:
第1类:大林和小林共有9本的话,有10种可能;
第2类:大林和小林共有8本的话,有9种可能;
第3类:大林和小林共有7本的话,有8种可能;
第4类:大林和小林共有6本的话,有7种可能;
第5类:大林和小林共有5本的话,有6种可能;
第6类:大林和小林共有4本的话,有5种可能;
第7类:大林和小林共有3本的话,有4种可能;
第8类:大林和小林共有2本的话,有3种可能;
第9类:大林和小林共有1本的话,有2种可能;
第10类:大林和小林共有0本的话,有1种可能;
由加法原理,大林和小林各自有小人书的数目有10+9+8+7+6+5+4+3+2+1=55种可能的情
况。
2.【分析】
因为奇数+奇数+奇数=奇数、奇数+奇数+偶数=偶数、
奇数+偶数+偶数=奇数、偶数+偶数+偶数=偶数;
要使3个数字之和为奇数,则这3个数字为三个奇数或一奇两偶,
由于放三个正方体可认为是一个一个地放分2类考虑:
第1类,3个数字同为奇数,出现奇数为1、3、5,有3种可能;放第1、2、3个正方体时,各有3
种可能;
由乘法原理,3个数字同为奇数,共有3×3×3=27种不同的情形。
第2类,3个数字为一奇两偶,出现奇数为1、3、5,有3种可能;出现偶数为2、4、6,有3种可
能;放第1、2、3个正方体时,各有3种可能;出现奇数的正方体的顺序有3种情况;
由乘法原理,3个数字为一奇两偶,共有(3×3×3)×3=81种不同的情形。
由加法原理,3个正方体向上的一面数字之和为奇数的共有27+81=108种不同的情形。
3.【分析】
按照位数分5类考虑:
第1类,一位数为3、有1个;
第2类,两位数的数码为1、2或1、5或2、4或4、5,共4组,由乘法原理,每一组可以组成
2×1=2种情况,共有2×4=8个不同的两位数;
第3类,三位数的数码为1、2、3或1、3、5或2、3、4或3、4、5,共4组,由乘法原理,每一
组可以组成3×2×1=6种情况,共可以组成6×4=24个不同的三位数;
第4类,四位数的数码为1、2、4、5,由乘法原理,有4×3×2×1=24个不同的四位数;
第5类,五位数的数码为1、2、3、4、5,由乘法原理,有5×4×3×2×1=120个不同的五位数;
由加法原理,用1、2、3、4、5五个数字,不许重复,位数不限,能写出1+8+24+24+120=177
个3的倍数。
4.【分析】
略
5.【分析】
每节有3种颜色可选,由乘法原理有3×3×3×3×3=35=243种涂法;
其中有些圆棒顺着看和倒着看颜色不一样,却被计算了2次;
有些圆棒顺着看与倒着看颜色一样,这种情况的玩具棒没有被重复计算,
这样的圆棒关于中心对称,有 3×3×3=27种涂法;
可以得到(243-27)÷2+27=135或(243+27)÷2=135种颜色不同的圆棒。
6.【分析】
对G进行分类讨论:
当选G当钳工时,从A、B、C中再选出1个钳工,有3种选法;
从D、E、F中选出2个电工,考虑谁没有被选上,有3种选法;
由乘法原理有3×3=9种;
当选G当电工时,从A、B、C中选出2个钳工,考虑谁没有被选上,有3种选法;
从D、E、F中再选出1个电工,有3种选法;
由乘法原理有3×3=9种;
当不选G时,有3×3=9种;
从A、B、C中选出2个钳工,考虑谁没有被选上,有3种选法;
从D、E、F中选出2个电工,考虑谁没有被选上,有3种选法;
由乘法原理有3×3=9种;
由加法原理,从这7个人中挑选若干人去完成这项工作,共有9+9+9=27种。
7.【分析】
插板法:8名广播员有7个间隔,要分成6份,需要5个间隔,即有两个间隔不需要插板。
所以有7×6÷2=21种方案。
同课章节目录
