小升初必考专题:容斥原理(讲义)-2020-2021学年数学六年级下册(含答案)全国通用
文档属性
| 名称 | 小升初必考专题:容斥原理(讲义)-2020-2021学年数学六年级下册(含答案)全国通用 |

|
|
| 格式 | docx | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览

文档简介
(
容斥原理
)
(
知识要点
)
容斥原理属于杯赛中常考的内容。在计数时,必须注意无一重复,无一遗漏。
为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
在一些计数问题中,经常遇到有关集合元素个数的计算。求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成: A∪B=A+B-A∩B (其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思;符号“∩”读作“交”,相当于中文“且”的意思。),则称这一公式为包含与排除原理,简称容斥原理。
图示如下:
A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A∩B,即阴影面积。
1.先包含——A+B
重叠部分A∩B计算了2次,多加了1次;
2.再排除——A+B -A∩B
把多加了1次的重叠部分A∩B减去。
A类、B类与C元素个数的总和=A类元素的个数+B类元素个数+C类元素个数-既是A类又是B类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数。
用符号表示为:
A∪B∪C=A+B+C-A∩B-B∩C-A∩C+A∩B∩C …
(
例
1
四年级同学参加学校举行的运动会,参加了百米跑、跳高、跳远这三个项目。参加百米跑的有
24
人,参加跳高的有
28
人,参加跳远的有
26
人;既参加百米跑又参加跳高的有
12
人,既参加跳高又参加跳远的有
9
人,既参加百米跑又参加跳远的有
14
人;三项都参加的有
5
人。四年级同学参加运动会比赛的共有
( )
人。
)
(
例
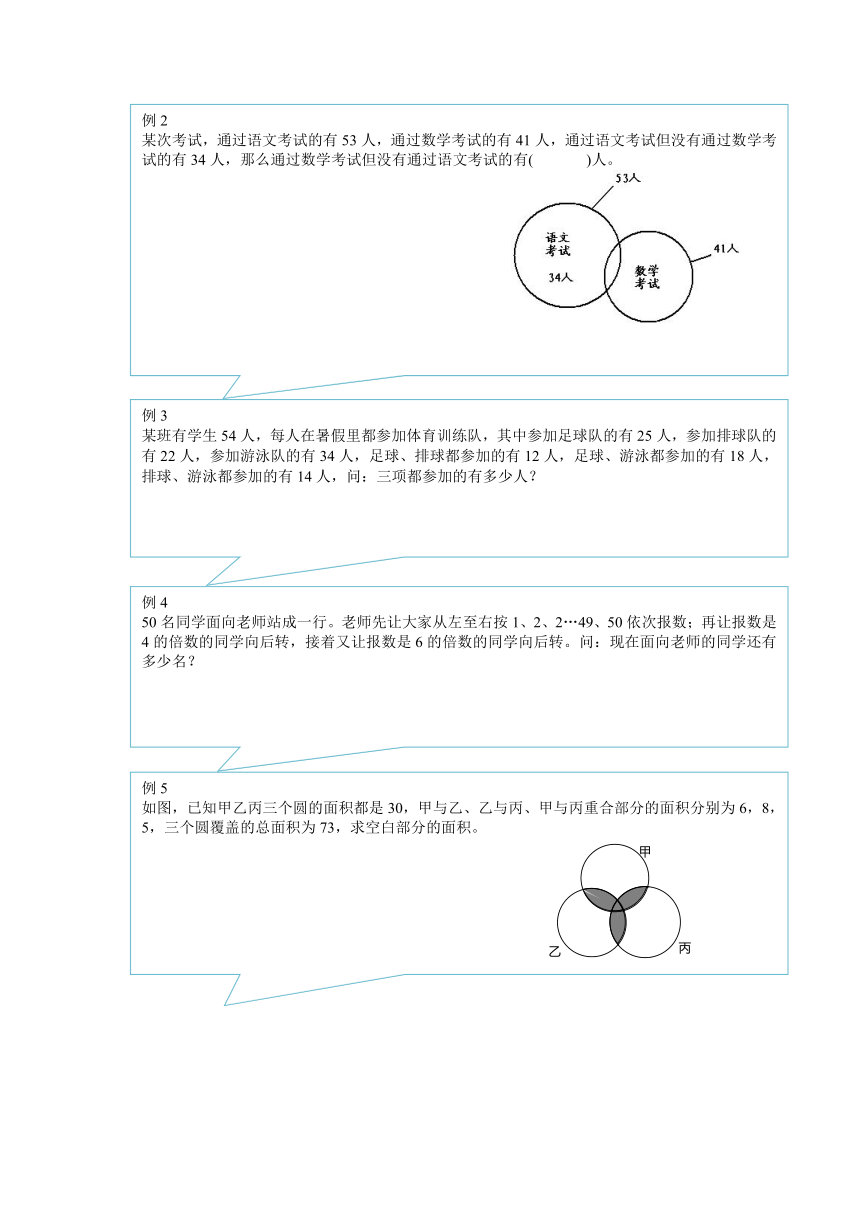
2
某次考试,通过语文考试的有
53
人,通过数学考试的有
41
人,通过语文考试但没有通过数学考试的有
34
人,那么通过数学考试但没有通过语文考试的有
( )
人。
)
(
例
3
某班有学生
54
人,每人在暑假里都参加体育训练队,其中参加足球队的有
25
人,参加排球队的有
22
人,参加游泳队的有
34
人,足球、排球都参加的有
12
人,足球、游泳都参加的有
18
人,排球、游泳都参加的有
14
人,问:三项都参加的有多少人?
)
(
例
4
50
名同学面向老师站成一行。老师先让大家从左至右按
1
、
2
、
2
…
49
、
50
依次报数;再让报数是
4
的倍数的同学向后转,接着又让报数是
6
的倍数的同学向后转。问:现在面向老师的同学还有多少名?
) (
例
5
如图,已知甲乙丙三个圆的面积都是
30
,甲与乙、乙与丙、甲与丙重合部分的面积分别为
6
,
8
,
5
,三个圆覆盖
的总面积为
73
,求空白部分的面积。
)
(
例
6
有
2000
盏亮着的电灯,各有一个拉线开关控制着,现按其顺序标号为
1
、
2
、
3
…
2000
,然后将编号为
2
的倍数的灯线拉一下,再将编号为
3
的倍数的灯线拉一下,最后将编号为
5
的倍数的灯线拉一下,
3
次拉完后亮着的灯有多少盏?
)
(
例
7
(
第六届“中环杯”五年级初赛
)
甲、乙、丙三人浇花,甲浇了
68
盆,乙浇了
62
盆,丙浇了
56
盆。已知共有花
90
盆,则三人都浇了的花至少有多少盆?
)
测试题
1.希望小学四年级有50名学生,有26人参加乒乓比赛,21人参加篮球比赛,两项比赛都不参加的有17人。两项比赛都参加的有( )人。
2.某大学某班学生总数为人,在第一次考试中有人及格,在第二次考试中有人及格,若两次
考试中,都没有及格的有人,那么两次考试都及格的人数是( )。
3.有位旅客,其中有人既不懂英语又不懂俄语,有人懂英语,人懂俄语。问既懂英语又懂俄语的有多少人?
4.有一根长厘米的绳子,从左端开始每隔厘米做一个记号,每隔厘米也做一个记号,然后将标有记号的地方剪断,问绳子共被剪成多少段?
5.二年级一班共名同学,其中少先队员人。这个班男生人,女生中有人不是少先队员,男生中有多少人是少先队员?
6.有三个面积各为平方厘米的圆纸片放在桌面上。三个纸片共同重叠的面积是平方厘米,三个纸片盖住桌面的总面积是平方厘米。问:图中阴影部分的面积之和是多少?
7.五年级班有名学生参加三项课外活动,其中人参加了绘画小组,人参加了合唱小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的倍,又是三项活动都参加人数的倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的倍,既参加绘画小组又参加合唱小组的有人,求参加朗诵小组的人数。
8.甲、乙、丙三人同时在读同样的故事书,书中有个故事,每个人都从某一个故事开始,按顺序往后读,已知甲读了个故事,乙读了个故事,丙读了个故事,那么甲、乙、丙人共同读过的故事最少有多少个?
答案
1.【分析】
【法二】:将参加乒乓球的人看成A类元素,参加篮球的人作为B类元素,那么参赛总人数为
接下来根据公式,可以知道
人。
【法二】:根据韦恩图,设所求部分人数为人,那么整体就分为四块,人数分别为17人,
。那么,所以人。
2.【分析】设第一次考试中及格的人(),第二次考试中及格的人()
显然,;,
则根据公式
那么两次考试都及格的人数是人。
3.【分析】
(法)在人中懂英语或俄语的有:(人)。
又因为有人懂英语,所以只懂俄语的有:(人)。
从位懂俄语的旅客中除去只懂俄语的人,剩下的人就是既懂英语又懂俄语的旅
客。
(法)在人中懂英语或俄语的有:(人)学会把公式进行适当得变换,由包含与排除
原理,得:(人)
4.【分析】
每隔厘米做一个记号,记号有(个),每隔厘米做一个记号,记号有
(个),因为,所以其中重合的记号有(个),
绳子上共有(个)记号,绳子被剪成(段)。
5.【分析】
二年级一班共名同学,这个班男生人,这个班女生人,女生中有人不是少先队
员,女生中有人是少先队员,男生中有人是少先队员。
6.【分析】
设阴影部分为,则,解得。或者平方厘米
7.【分析】
三项都参加的人数为,参加朗诵小组的为,既参加绘画小组又参加朗诵小组的人数为,
既参加朗诵小组又参加合唱小组的人数也为。
根据公式列出方程,解得,所以参加朗诵小组的人数为
人。
8.【分析】
先考虑甲、乙两个人,甲、乙都读过的故事至少有(个),甲单独看的故事是
(个),乙单独看的故事有(个),要使三人共同读过的故事最少,则丙应该尽
量读甲或乙单独看的故事,所以三人共同看过的故事最少有(个)。
容斥原理
)
(
知识要点
)
容斥原理属于杯赛中常考的内容。在计数时,必须注意无一重复,无一遗漏。
为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
在一些计数问题中,经常遇到有关集合元素个数的计算。求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成: A∪B=A+B-A∩B (其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思;符号“∩”读作“交”,相当于中文“且”的意思。),则称这一公式为包含与排除原理,简称容斥原理。
图示如下:
A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A∩B,即阴影面积。
1.先包含——A+B
重叠部分A∩B计算了2次,多加了1次;
2.再排除——A+B -A∩B
把多加了1次的重叠部分A∩B减去。
A类、B类与C元素个数的总和=A类元素的个数+B类元素个数+C类元素个数-既是A类又是B类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数。
用符号表示为:
A∪B∪C=A+B+C-A∩B-B∩C-A∩C+A∩B∩C …
(
例
1
四年级同学参加学校举行的运动会,参加了百米跑、跳高、跳远这三个项目。参加百米跑的有
24
人,参加跳高的有
28
人,参加跳远的有
26
人;既参加百米跑又参加跳高的有
12
人,既参加跳高又参加跳远的有
9
人,既参加百米跑又参加跳远的有
14
人;三项都参加的有
5
人。四年级同学参加运动会比赛的共有
( )
人。
)
(
例
2
某次考试,通过语文考试的有
53
人,通过数学考试的有
41
人,通过语文考试但没有通过数学考试的有
34
人,那么通过数学考试但没有通过语文考试的有
( )
人。
)
(
例
3
某班有学生
54
人,每人在暑假里都参加体育训练队,其中参加足球队的有
25
人,参加排球队的有
22
人,参加游泳队的有
34
人,足球、排球都参加的有
12
人,足球、游泳都参加的有
18
人,排球、游泳都参加的有
14
人,问:三项都参加的有多少人?
)
(
例
4
50
名同学面向老师站成一行。老师先让大家从左至右按
1
、
2
、
2
…
49
、
50
依次报数;再让报数是
4
的倍数的同学向后转,接着又让报数是
6
的倍数的同学向后转。问:现在面向老师的同学还有多少名?
) (
例
5
如图,已知甲乙丙三个圆的面积都是
30
,甲与乙、乙与丙、甲与丙重合部分的面积分别为
6
,
8
,
5
,三个圆覆盖
的总面积为
73
,求空白部分的面积。
)
(
例
6
有
2000
盏亮着的电灯,各有一个拉线开关控制着,现按其顺序标号为
1
、
2
、
3
…
2000
,然后将编号为
2
的倍数的灯线拉一下,再将编号为
3
的倍数的灯线拉一下,最后将编号为
5
的倍数的灯线拉一下,
3
次拉完后亮着的灯有多少盏?
)
(
例
7
(
第六届“中环杯”五年级初赛
)
甲、乙、丙三人浇花,甲浇了
68
盆,乙浇了
62
盆,丙浇了
56
盆。已知共有花
90
盆,则三人都浇了的花至少有多少盆?
)
测试题
1.希望小学四年级有50名学生,有26人参加乒乓比赛,21人参加篮球比赛,两项比赛都不参加的有17人。两项比赛都参加的有( )人。
2.某大学某班学生总数为人,在第一次考试中有人及格,在第二次考试中有人及格,若两次
考试中,都没有及格的有人,那么两次考试都及格的人数是( )。
3.有位旅客,其中有人既不懂英语又不懂俄语,有人懂英语,人懂俄语。问既懂英语又懂俄语的有多少人?
4.有一根长厘米的绳子,从左端开始每隔厘米做一个记号,每隔厘米也做一个记号,然后将标有记号的地方剪断,问绳子共被剪成多少段?
5.二年级一班共名同学,其中少先队员人。这个班男生人,女生中有人不是少先队员,男生中有多少人是少先队员?
6.有三个面积各为平方厘米的圆纸片放在桌面上。三个纸片共同重叠的面积是平方厘米,三个纸片盖住桌面的总面积是平方厘米。问:图中阴影部分的面积之和是多少?
7.五年级班有名学生参加三项课外活动,其中人参加了绘画小组,人参加了合唱小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的倍,又是三项活动都参加人数的倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的倍,既参加绘画小组又参加合唱小组的有人,求参加朗诵小组的人数。
8.甲、乙、丙三人同时在读同样的故事书,书中有个故事,每个人都从某一个故事开始,按顺序往后读,已知甲读了个故事,乙读了个故事,丙读了个故事,那么甲、乙、丙人共同读过的故事最少有多少个?
答案
1.【分析】
【法二】:将参加乒乓球的人看成A类元素,参加篮球的人作为B类元素,那么参赛总人数为
接下来根据公式,可以知道
人。
【法二】:根据韦恩图,设所求部分人数为人,那么整体就分为四块,人数分别为17人,
。那么,所以人。
2.【分析】设第一次考试中及格的人(),第二次考试中及格的人()
显然,;,
则根据公式
那么两次考试都及格的人数是人。
3.【分析】
(法)在人中懂英语或俄语的有:(人)。
又因为有人懂英语,所以只懂俄语的有:(人)。
从位懂俄语的旅客中除去只懂俄语的人,剩下的人就是既懂英语又懂俄语的旅
客。
(法)在人中懂英语或俄语的有:(人)学会把公式进行适当得变换,由包含与排除
原理,得:(人)
4.【分析】
每隔厘米做一个记号,记号有(个),每隔厘米做一个记号,记号有
(个),因为,所以其中重合的记号有(个),
绳子上共有(个)记号,绳子被剪成(段)。
5.【分析】
二年级一班共名同学,这个班男生人,这个班女生人,女生中有人不是少先队
员,女生中有人是少先队员,男生中有人是少先队员。
6.【分析】
设阴影部分为,则,解得。或者平方厘米
7.【分析】
三项都参加的人数为,参加朗诵小组的为,既参加绘画小组又参加朗诵小组的人数为,
既参加朗诵小组又参加合唱小组的人数也为。
根据公式列出方程,解得,所以参加朗诵小组的人数为
人。
8.【分析】
先考虑甲、乙两个人,甲、乙都读过的故事至少有(个),甲单独看的故事是
(个),乙单独看的故事有(个),要使三人共同读过的故事最少,则丙应该尽
量读甲或乙单独看的故事,所以三人共同看过的故事最少有(个)。
同课章节目录
