2021-2022学年鲁教版(五四制)七年级数学下册8.5平行线的性质定理 训练(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学下册8.5平行线的性质定理 训练(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版七年级数学下册《8-5平行线的性质定理》优生辅导训练(附答案)
一.选择题
1.如图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上,已知∠1=55°,则∠2的度数为( )
A.45° B.35° C.55° D.125°
2.如图AB∥CD,则∠1=( )
A.75° B.80° C.85° D.145°
3.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140°
B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向右拐40°,第二次向右拐40°
4.如图,下列判断中错误的是( )
A.由∠A+∠ADC=180°得到AB∥CD
B.由AB∥CD得到∠ABC+∠C=180°
C.由∠1=∠2得到AD∥BC
D.由AD∥BC得到∠3=∠4
5.如图,已知AB∥CD,CE平分∠ACD,且∠A=120°,则∠1=( )
A.45° B.60° C.40° D.30°
6.如图所示,l1∥l2,三角板ABC如图放置,其中∠B=90°,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.60° D.30°
7.AF是∠BAC的平分线,DF∥AC,若∠BAC=70°,则∠1的度数为( )
A.175° B.35° C.55° D.70°
8.如图所示,直线a、b、c、d的位置如图所示,若∠1=125°,∠2=125°,∠3=135°,则∠4的度数为( )
A.45° B.55° C.60° D.65°
二.填空题
9.如图,已知直线AB、CD被直线AE所截,AB∥CD,∠2=130°,则∠1= .
10.平面内∠A和∠B的两边互相平行,且∠A=40°,则∠B= .
11.如图,若AB∥CD,∠1=30°,则∠2= °.
三.解答题
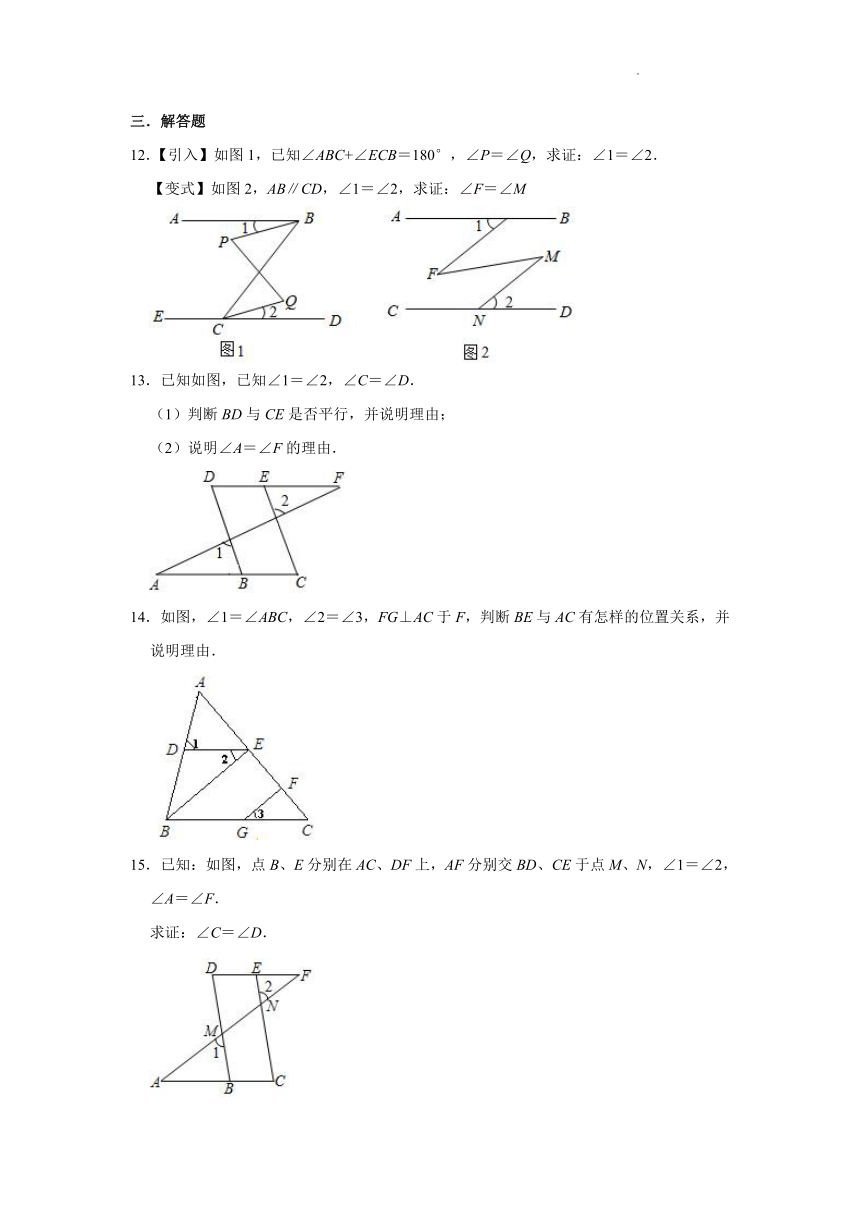
12.【引入】如图1,已知∠ABC+∠ECB=180°,∠P=∠Q,求证:∠1=∠2.
【变式】如图2,AB∥CD,∠1=∠2,求证:∠F=∠M
13.已知如图,已知∠1=∠2,∠C=∠D.
(1)判断BD与CE是否平行,并说明理由;
(2)说明∠A=∠F的理由.
14.如图,∠1=∠ABC,∠2=∠3,FG⊥AC于F,判断BE与AC有怎样的位置关系,并说明理由.
15.已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
求证:∠C=∠D.
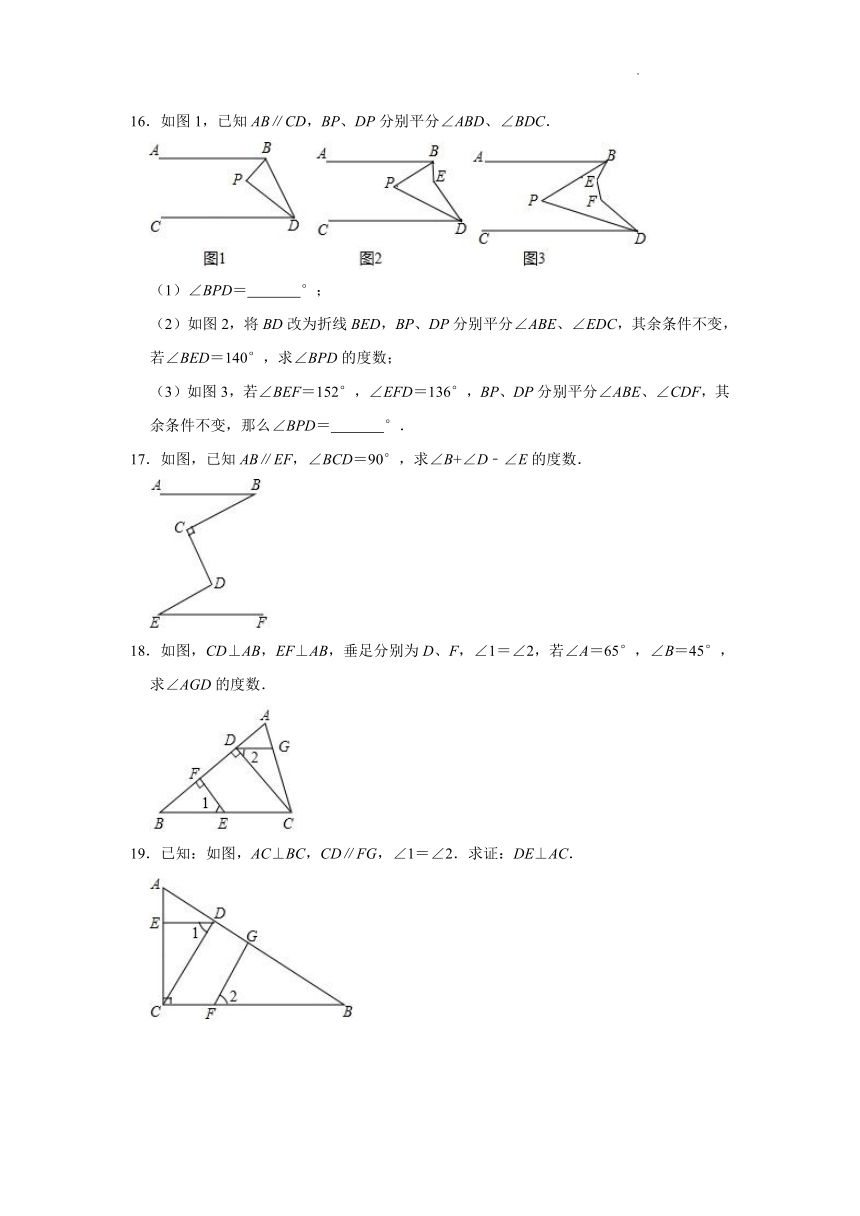
16.如图1,已知AB∥CD,BP、DP分别平分∠ABD、∠BDC.
(1)∠BPD= °;
(2)如图2,将BD改为折线BED,BP、DP分别平分∠ABE、∠EDC,其余条件不变,若∠BED=140°,求∠BPD的度数;
(3)如图3,若∠BEF=152°,∠EFD=136°,BP、DP分别平分∠ABE、∠CDF,其余条件不变,那么∠BPD= °.
17.如图,已知AB∥EF,∠BCD=90°,求∠B+∠D﹣∠E的度数.
18.如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,若∠A=65°,∠B=45°,求∠AGD的度数.
19.已知:如图,AC⊥BC,CD∥FG,∠1=∠2.求证:DE⊥AC.
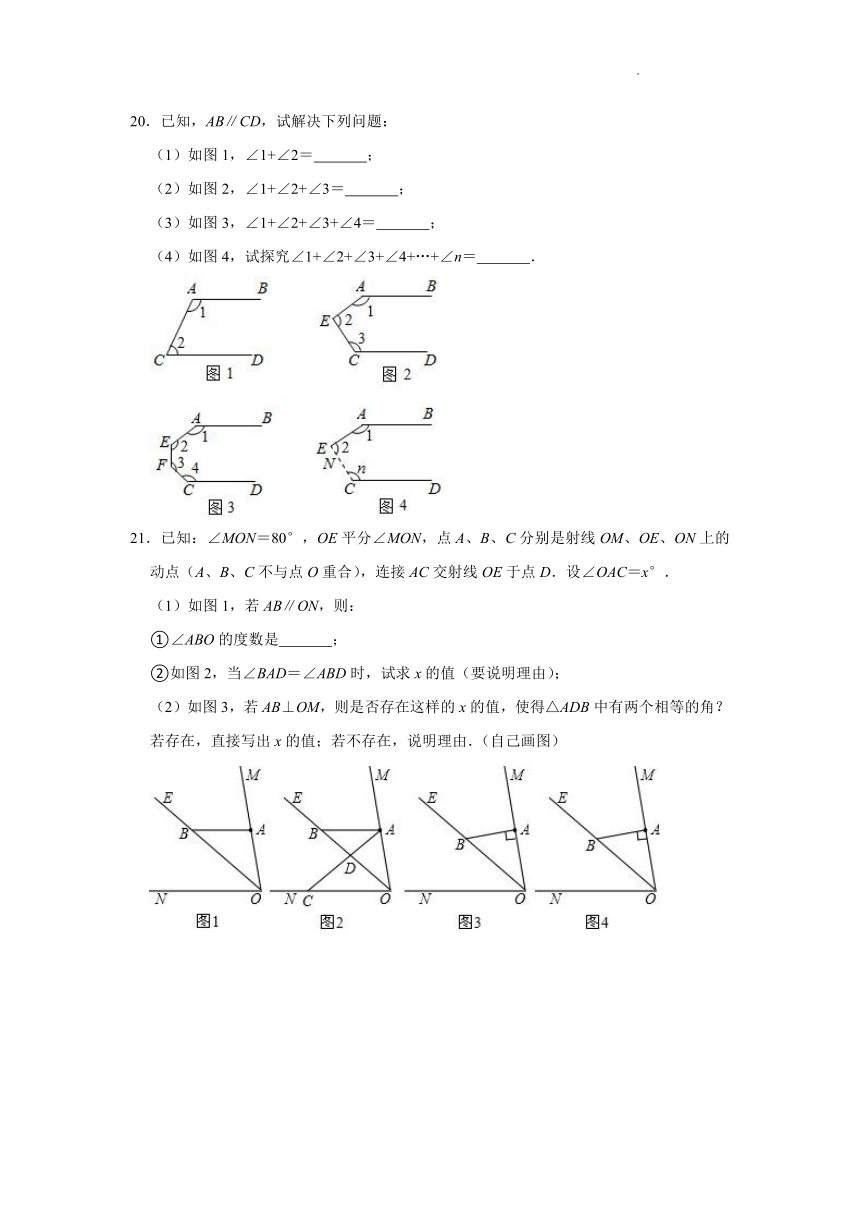
20.已知,AB∥CD,试解决下列问题:
(1)如图1,∠1+∠2= ;
(2)如图2,∠1+∠2+∠3= ;
(3)如图3,∠1+∠2+∠3+∠4= ;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n= .
21.已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:
①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)
参考答案
一.选择题
1.解:∵a∥b,
∴∠1=∠3=55°,
∵∠3+∠2+90°=180°,
∴∠2+∠3=90°,
∴∠2=90°﹣55°=35°,
故选:B.
2.解:延长BE交CD于点F.
∵AB∥CD,
∴∠B+∠BFD=180°,
∴∠BFD=180°﹣∠B=180°﹣120°=60°,
∴∠1=∠ECD+∠BFD=25°+60°=85°.
故选:C.
3.解:A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选:B.
4.解:A、由∠A+∠ADC=180°得到AB∥CD(同旁内角互补,两直线平行),正确;
B、由AB∥CD得到∠ABC+∠C=180°(两直线平行,同旁内角互补),正确;
C、由∠1=∠2得到AD∥BC(内错角相等,两直线平行),正确;
D、由AD∥BC得到∠1=∠2(两直线平行,内错角相等),所以此选项错误.
故选:D.
5.解:∵AB∥CD,
∴∠1=∠DCE,∠A+∠ACD=180°,
又∵∠A=120°,
∴∠ACD=60°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=∠ACD=30°,
∴∠1=30°,
故选:D.
6.解:作BD∥l1,如图所示:
∵BD∥l1,∠1=40°,
∴∠1=∠ABD=40°,
又∵l1∥l2,
∴BD∥l2,
∴∠CBD=∠2,
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠CBD=50°,
∴∠2=50°.
故选:B.
7.解:∵∠BAC=70°,AF平分∠BAC,
∴∠FAC=∠BAC=35°,
∵DF∥AC,
∴∠1=∠FAC=35°,
故选:B.
8.解:如图所示,∵∠1=125°,∠2=125°,
∴a∥b,
∴∠4=∠5,
又∵∠3=135°,
∴∠5=45°,
∴∠4=45°,
故选:A.
二.填空题
9.解:如图:
∵∠2=130°,
∴∠3=180°﹣∠2=50°,
∵AB∥CD,
∴∠1=∠3=50°.
故答案为:50°.
10.解:如图1所示,
∵∠A和∠B的两边互相平行,
∴∠A=∠1,∠1=∠B.
∴∠B=∠A=40°;
如图2所示,
∵∠A和∠B的两边互相平行,
∴∠A=∠1,∠1+∠B=180°.
∴∠B=140°;
故答案为:40°或140°.
11.解:如图,∵AB∥CD,
∴∠1=∠3=30°,
又∵∠2+∠3=180°,
∴∠2=180°﹣30°=150°,
故答案为:150.
三.解答题
12.【引入】证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
【变式】证明:延长EF交CD于G,如图:
∵AB∥CD,
∴∠1=∠EGD
∵∠1=∠2,
∴∠EGD=∠2
∴EF∥MN,
∴∠EFM=∠M.
13.解:(1)BD∥CE,理由如下:
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE;
(2)理由如下:∵BD∥CE,
∴∠C=∠4.
∵∠C=∠D,
∴∠D=∠4,
∴AC∥DF,
∴∠A=∠F.
14.解:BE⊥AC.
理由:
∵∠1=∠ABC,
∴DE∥BC,
∴∠2=∠EBC而∠2=∠3,
∴∠3=∠EBC,
∴FG∥BE又FG⊥AC,
∴BE⊥AC.
15.证明:∵∠ANC=∠2,∠1=∠2,
∴∠1=∠ANC,
∴DB∥CE,
∴∠C=∠ABD,
∵∠A=∠F,
∴DF∥AC,
∴∠D=∠ABD,
∴∠C=∠D.
16.解:(1)∵AB∥CD,
∴∠ABD+∠BDC=∠180°,
∵BP、DP分别平分∠ABD、∠BDC,
∴∠PBD+∠PDB=90°,
∴∠BPD=180°﹣90°=90°.
(2)连接BD,
∵∠BED=140°,
∴∠EBD+∠EDB=40°,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BP、DP分别平分∠ABE、∠EDC,
∴∠PBE=∠ABE,∠PDE=∠CDE,
∴∠PBE+∠PDE=×(180°﹣40°)=70°,
∴∠BPD=180°﹣∠PBE﹣PDE﹣∠EBD﹣∠EDB=70°.
(3)连接BD,
∵∠BEF=152°,∠EFD=136°,
∴∠EBD+∠FDB=360°﹣(152°+136°)=72°,
∵BP、DP分别平分∠ABE、∠FDC,
∴∠PBE=∠ABE,∠PDF=∠CDF,
∴∠PBE+∠PDF=×(180°﹣72°)=54°,
∴∠BPD=180°﹣(∠EBD+∠FDB)﹣(∠PBE+∠PDF)=54°.
故答案为:90;54°.
17.解:过点C作直线CM∥AB,过点D作直线DN∥EF,给各角表示序号,如图所示.
∵AB∥EF,CM∥AB,DN∥EF,
∴CM∥DN,
∴∠B=∠1,∠2=∠3,∠4=∠E,
∴∠CDE﹣∠E=∠3+∠4﹣∠E=∠3=∠2,
∴∠B+∠CDE﹣∠E=∠B+∠2=∠1+∠2=∠BCD=90°.
18.解:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF,
∴∠DCB=∠1.
∵∠1=∠2,
∴∠DCB=∠2,
∴DG∥BC,
∴∠ADG=∠B=45°.
又∵在△ADG中,∠A=65°,∠ADG=45°,
∴∠AGD=180°﹣∠A﹣∠ADG=70°.
19.证明:∵CD∥FG,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DE∥BC,
∵AC⊥BC,
∴DE⊥AC.
20.
解:(1)∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补);
(2)过点E作一条直线EF∥AB,
∵AB∥CD,
∴CD∥EF,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠2+∠3=360°;
(3)过点E、F作EG、FH平行于AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°;
∴∠1+∠2+∠3+∠4=540°;
(4)根据上述规律,显然作(n﹣2)条辅助线,运用(n﹣1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n﹣1).
21.解:(1)①∵∠MON=80°,OE平分∠MON.
∴∠AOB=∠BON=40°,
∵AB∥ON,
∴∠ABO=40°.
故答案是:40°;
②如答图1,∵∠MON=80°,且OE平分∠MON,
∴∠1=∠2=40°,
又∵AB∥ON,
∴∠3=∠1=40°,
∵∠BAD=∠ABD,
∴∠BAD=40°
∴∠4=80°,
∴∠OAC=60°,即x=60.
(2)存在这样的x,
①如答图2,当点D在线段OB上时,
若∠BAD=∠ABD,则x=40;
若∠BAD=∠BDA,则x=25;
若∠ADB=∠ABD,则x=10.
②如答图3,当点D在射线BE上时,因为∠ABE=130°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=115,C不在ON上,舍去;
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=10、25、40.
一.选择题
1.如图,小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上,已知∠1=55°,则∠2的度数为( )
A.45° B.35° C.55° D.125°
2.如图AB∥CD,则∠1=( )
A.75° B.80° C.85° D.145°
3.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )
A.第一次向右拐40°,第二次向左拐140°
B.第一次向左拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向右拐40°,第二次向右拐40°
4.如图,下列判断中错误的是( )
A.由∠A+∠ADC=180°得到AB∥CD
B.由AB∥CD得到∠ABC+∠C=180°
C.由∠1=∠2得到AD∥BC
D.由AD∥BC得到∠3=∠4
5.如图,已知AB∥CD,CE平分∠ACD,且∠A=120°,则∠1=( )
A.45° B.60° C.40° D.30°
6.如图所示,l1∥l2,三角板ABC如图放置,其中∠B=90°,若∠1=40°,则∠2的度数是( )
A.40° B.50° C.60° D.30°
7.AF是∠BAC的平分线,DF∥AC,若∠BAC=70°,则∠1的度数为( )
A.175° B.35° C.55° D.70°
8.如图所示,直线a、b、c、d的位置如图所示,若∠1=125°,∠2=125°,∠3=135°,则∠4的度数为( )
A.45° B.55° C.60° D.65°
二.填空题
9.如图,已知直线AB、CD被直线AE所截,AB∥CD,∠2=130°,则∠1= .
10.平面内∠A和∠B的两边互相平行,且∠A=40°,则∠B= .
11.如图,若AB∥CD,∠1=30°,则∠2= °.
三.解答题
12.【引入】如图1,已知∠ABC+∠ECB=180°,∠P=∠Q,求证:∠1=∠2.
【变式】如图2,AB∥CD,∠1=∠2,求证:∠F=∠M
13.已知如图,已知∠1=∠2,∠C=∠D.
(1)判断BD与CE是否平行,并说明理由;
(2)说明∠A=∠F的理由.
14.如图,∠1=∠ABC,∠2=∠3,FG⊥AC于F,判断BE与AC有怎样的位置关系,并说明理由.
15.已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
求证:∠C=∠D.
16.如图1,已知AB∥CD,BP、DP分别平分∠ABD、∠BDC.
(1)∠BPD= °;
(2)如图2,将BD改为折线BED,BP、DP分别平分∠ABE、∠EDC,其余条件不变,若∠BED=140°,求∠BPD的度数;
(3)如图3,若∠BEF=152°,∠EFD=136°,BP、DP分别平分∠ABE、∠CDF,其余条件不变,那么∠BPD= °.
17.如图,已知AB∥EF,∠BCD=90°,求∠B+∠D﹣∠E的度数.
18.如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,若∠A=65°,∠B=45°,求∠AGD的度数.
19.已知:如图,AC⊥BC,CD∥FG,∠1=∠2.求证:DE⊥AC.
20.已知,AB∥CD,试解决下列问题:
(1)如图1,∠1+∠2= ;
(2)如图2,∠1+∠2+∠3= ;
(3)如图3,∠1+∠2+∠3+∠4= ;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n= .
21.已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:
①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)
参考答案
一.选择题
1.解:∵a∥b,
∴∠1=∠3=55°,
∵∠3+∠2+90°=180°,
∴∠2+∠3=90°,
∴∠2=90°﹣55°=35°,
故选:B.
2.解:延长BE交CD于点F.
∵AB∥CD,
∴∠B+∠BFD=180°,
∴∠BFD=180°﹣∠B=180°﹣120°=60°,
∴∠1=∠ECD+∠BFD=25°+60°=85°.
故选:C.
3.解:A、如图1:∵∠1=40°,∠2=140°,
∴AB与CD不平行;
故本选项错误;
B、如图2:∵∠1=40°,∠2=40°,
∴∠1=∠2,
∴AB与CD平行;
故本选项正确;
C、如图3:∵∠1=40°,∠2=140°,
∴∠1≠∠2,
∴AB不平行CD;
故本选项错误;
D、如图4:∠1=40°,∠2=40°,
∴∠3=140°,
∴∠1≠∠3,
∴AB与CD不平行;
故本选项错误.
故选:B.
4.解:A、由∠A+∠ADC=180°得到AB∥CD(同旁内角互补,两直线平行),正确;
B、由AB∥CD得到∠ABC+∠C=180°(两直线平行,同旁内角互补),正确;
C、由∠1=∠2得到AD∥BC(内错角相等,两直线平行),正确;
D、由AD∥BC得到∠1=∠2(两直线平行,内错角相等),所以此选项错误.
故选:D.
5.解:∵AB∥CD,
∴∠1=∠DCE,∠A+∠ACD=180°,
又∵∠A=120°,
∴∠ACD=60°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=∠ACD=30°,
∴∠1=30°,
故选:D.
6.解:作BD∥l1,如图所示:
∵BD∥l1,∠1=40°,
∴∠1=∠ABD=40°,
又∵l1∥l2,
∴BD∥l2,
∴∠CBD=∠2,
又∵∠CBA=∠CBD+∠ABD=90°,
∴∠CBD=50°,
∴∠2=50°.
故选:B.
7.解:∵∠BAC=70°,AF平分∠BAC,
∴∠FAC=∠BAC=35°,
∵DF∥AC,
∴∠1=∠FAC=35°,
故选:B.
8.解:如图所示,∵∠1=125°,∠2=125°,
∴a∥b,
∴∠4=∠5,
又∵∠3=135°,
∴∠5=45°,
∴∠4=45°,
故选:A.
二.填空题
9.解:如图:
∵∠2=130°,
∴∠3=180°﹣∠2=50°,
∵AB∥CD,
∴∠1=∠3=50°.
故答案为:50°.
10.解:如图1所示,
∵∠A和∠B的两边互相平行,
∴∠A=∠1,∠1=∠B.
∴∠B=∠A=40°;
如图2所示,
∵∠A和∠B的两边互相平行,
∴∠A=∠1,∠1+∠B=180°.
∴∠B=140°;
故答案为:40°或140°.
11.解:如图,∵AB∥CD,
∴∠1=∠3=30°,
又∵∠2+∠3=180°,
∴∠2=180°﹣30°=150°,
故答案为:150.
三.解答题
12.【引入】证明:∵∠ABC+∠ECB=180°,
∴AB∥DE,
∴∠ABC=∠BCD,
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠ABC﹣∠PBC,∠2=∠BCD﹣∠BCQ,
∴∠1=∠2.
【变式】证明:延长EF交CD于G,如图:
∵AB∥CD,
∴∠1=∠EGD
∵∠1=∠2,
∴∠EGD=∠2
∴EF∥MN,
∴∠EFM=∠M.
13.解:(1)BD∥CE,理由如下:
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴BD∥CE;
(2)理由如下:∵BD∥CE,
∴∠C=∠4.
∵∠C=∠D,
∴∠D=∠4,
∴AC∥DF,
∴∠A=∠F.
14.解:BE⊥AC.
理由:
∵∠1=∠ABC,
∴DE∥BC,
∴∠2=∠EBC而∠2=∠3,
∴∠3=∠EBC,
∴FG∥BE又FG⊥AC,
∴BE⊥AC.
15.证明:∵∠ANC=∠2,∠1=∠2,
∴∠1=∠ANC,
∴DB∥CE,
∴∠C=∠ABD,
∵∠A=∠F,
∴DF∥AC,
∴∠D=∠ABD,
∴∠C=∠D.
16.解:(1)∵AB∥CD,
∴∠ABD+∠BDC=∠180°,
∵BP、DP分别平分∠ABD、∠BDC,
∴∠PBD+∠PDB=90°,
∴∠BPD=180°﹣90°=90°.
(2)连接BD,
∵∠BED=140°,
∴∠EBD+∠EDB=40°,
∵AB∥CD,
∴∠ABD+∠CDB=180°,
∵BP、DP分别平分∠ABE、∠EDC,
∴∠PBE=∠ABE,∠PDE=∠CDE,
∴∠PBE+∠PDE=×(180°﹣40°)=70°,
∴∠BPD=180°﹣∠PBE﹣PDE﹣∠EBD﹣∠EDB=70°.
(3)连接BD,
∵∠BEF=152°,∠EFD=136°,
∴∠EBD+∠FDB=360°﹣(152°+136°)=72°,
∵BP、DP分别平分∠ABE、∠FDC,
∴∠PBE=∠ABE,∠PDF=∠CDF,
∴∠PBE+∠PDF=×(180°﹣72°)=54°,
∴∠BPD=180°﹣(∠EBD+∠FDB)﹣(∠PBE+∠PDF)=54°.
故答案为:90;54°.
17.解:过点C作直线CM∥AB,过点D作直线DN∥EF,给各角表示序号,如图所示.
∵AB∥EF,CM∥AB,DN∥EF,
∴CM∥DN,
∴∠B=∠1,∠2=∠3,∠4=∠E,
∴∠CDE﹣∠E=∠3+∠4﹣∠E=∠3=∠2,
∴∠B+∠CDE﹣∠E=∠B+∠2=∠1+∠2=∠BCD=90°.
18.解:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF,
∴∠DCB=∠1.
∵∠1=∠2,
∴∠DCB=∠2,
∴DG∥BC,
∴∠ADG=∠B=45°.
又∵在△ADG中,∠A=65°,∠ADG=45°,
∴∠AGD=180°﹣∠A﹣∠ADG=70°.
19.证明:∵CD∥FG,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DE∥BC,
∵AC⊥BC,
∴DE⊥AC.
20.
解:(1)∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补);
(2)过点E作一条直线EF∥AB,
∵AB∥CD,
∴CD∥EF,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠2+∠3=360°;
(3)过点E、F作EG、FH平行于AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°;
∴∠1+∠2+∠3+∠4=540°;
(4)根据上述规律,显然作(n﹣2)条辅助线,运用(n﹣1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n﹣1).
21.解:(1)①∵∠MON=80°,OE平分∠MON.
∴∠AOB=∠BON=40°,
∵AB∥ON,
∴∠ABO=40°.
故答案是:40°;
②如答图1,∵∠MON=80°,且OE平分∠MON,
∴∠1=∠2=40°,
又∵AB∥ON,
∴∠3=∠1=40°,
∵∠BAD=∠ABD,
∴∠BAD=40°
∴∠4=80°,
∴∠OAC=60°,即x=60.
(2)存在这样的x,
①如答图2,当点D在线段OB上时,
若∠BAD=∠ABD,则x=40;
若∠BAD=∠BDA,则x=25;
若∠ADB=∠ABD,则x=10.
②如答图3,当点D在射线BE上时,因为∠ABE=130°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=115,C不在ON上,舍去;
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=10、25、40.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
