北师大版数学七年级下册 3.1用表格表示的变量间关系 课件(共16张)
文档属性
| 名称 | 北师大版数学七年级下册 3.1用表格表示的变量间关系 课件(共16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第三章 变量之间的关系
3.1 用表格表示的变量间关系
知识点 变量与常量
1.在用电水壶加热水的过程中,电水壶里的水温随通电时间的长短而变化,这个问题中的变量是( )
A.通电的强弱 B.通电的时间和通电的强弱
C.通电的时间和水的温度 D.电水壶
2.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
C
C
3.三角形ABC中,设BC=a,BC边上的高为h,三角形ABC的面积为S,则S= ah,当点A的位置发生变化,B,C的位置不变时,则变量是( )
A.S,a B.S,h C.h,a D.S,h,a
B
知识点 自变量与因变量
4.在利用太阳能热水器加热的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
5.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
B
D
6.用总长为60 m的篱笆围成长方形场地,宽随长的增大而_______.
减小
知识点 用表格表示变量之间的关系
7.某河流受暴雨袭击,某天的河水水位记录如下表:
时间/h 0 4 8 12 16 20 24
水位/m 2 2.65 3 4 5 6 8
(1)上表反映的是_______与________两个变量之间的关系,其中自变量是________,因变量是_________;
(2)在_____时至_____时内,水位上升最慢.
水位
时间
时间
水位
4
8
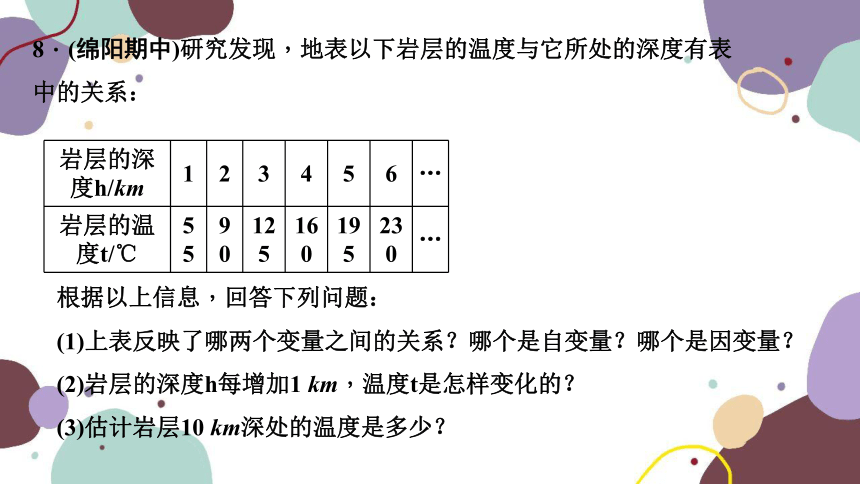
8.(绵阳期中)研究发现,地表以下岩层的温度与它所处的深度有表中的关系:
岩层的深
度h/km 1 2 3 4 5 6 …
岩层的温
度t/℃ 55 90 125 160 195 230 …
根据以上信息,回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)岩层的深度h每增加1 km,温度t是怎样变化的?
(3)估计岩层10 km深处的温度是多少?
解:(1)上表反映了岩层的深度h(km)与岩层的温度t(℃)之间的关系;其中岩层深度h(km)是自变量,岩层的温度t(℃)是因变量
(2)岩层的深度h每增加1 km,温度t上升35 ℃,关系式:t=55+35(h-1)=35h+20
(3)当h=10 km时,t=35×10+20=370(℃)
9.根据科学研究表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)之间的关系如下表所示:下列说法不正确的是( )
x/kg 0 1 2 3 4 5
y/cm 20 20.5 21 21.5 22 22.5
B
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0 cm
C.随着所挂物体的重量增加,弹簧长度逐渐变长
D.所挂物体的重量每增加1 kg,弹簧长度增加0.5 cm
10.(德阳期末)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度(℃) -20 -10 0 10 20 30
声速(m/s) 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20 ℃时,声音5 s可以传播1740 m
D.当温度每升高10 ℃,声速增加6 m/s
C
11.随着我国人口增长速度的减慢,小学入学儿童数量有所减少,表中的数据近似地呈现了某地区入学儿童的变化趋势.
年份(x) 2016 2017 2018 …
入学儿童人数(y) 2520 2330 2140 …
(1)上表中________是自变量,________________是因变量;
(2)你预计该地区从______年起入学儿童的人数在1600人左右.
年份
入学儿童人数
2021
12. 如表是某报纸公布的世界人口数据情况:
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
年份 1957 1974 1987 1999 2010 2025
人口数 30亿 40亿 50亿 60亿 70亿 80亿
解:(1)表中有两个变量,分别是年份和人口数
(2)用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是增大
13.下表给出了橘农王林去年橘子的销售额(元)随橘子卖出质量(千克)的变化的有关数据:
卖出质量(千克) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是多少?
(3)估计当橘子卖出50千克时,销售额是多少?
解:(1)表中反映了橘子的卖出质量与销售额之间的关系,橘子的卖出质量是自变量,销售额是因变量
(2)当橘子卖出5千克时,销售额为10元
(3)当橘子卖出50千克时,销售额为100元
14.已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:
底面半径x(cm) 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量y(cm3) 6.9 6.0 5.6 5.5 5.7 6.0 6.5
(1)上表反映了易拉罐底面半径和用铝量两个变量之间的关系,哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4 cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由;
(4)粗略说一说易拉罐底面半径对所需铝质量的影响.
解:(1)易拉罐底面半径为自变量,用铝量为因变量
(2)当底面半径为2.4 cm时,易拉罐的用铝量为5.6 cm3
(3)易拉罐底面半径为2.8 cm时比较合适,∵此时用铝较少,成本低
(4)当易拉罐底面半径在1.6 cm~2.8 cm变化时,用铝量随半径的增大而减小,当易拉罐底面半径在2.8 cm~4.0 cm间变化时,用铝量随半径的增大而增大
第三章 变量之间的关系
3.1 用表格表示的变量间关系
知识点 变量与常量
1.在用电水壶加热水的过程中,电水壶里的水温随通电时间的长短而变化,这个问题中的变量是( )
A.通电的强弱 B.通电的时间和通电的强弱
C.通电的时间和水的温度 D.电水壶
2.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
C
C
3.三角形ABC中,设BC=a,BC边上的高为h,三角形ABC的面积为S,则S= ah,当点A的位置发生变化,B,C的位置不变时,则变量是( )
A.S,a B.S,h C.h,a D.S,h,a
B
知识点 自变量与因变量
4.在利用太阳能热水器加热的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
5.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
B
D
6.用总长为60 m的篱笆围成长方形场地,宽随长的增大而_______.
减小
知识点 用表格表示变量之间的关系
7.某河流受暴雨袭击,某天的河水水位记录如下表:
时间/h 0 4 8 12 16 20 24
水位/m 2 2.65 3 4 5 6 8
(1)上表反映的是_______与________两个变量之间的关系,其中自变量是________,因变量是_________;
(2)在_____时至_____时内,水位上升最慢.
水位
时间
时间
水位
4
8
8.(绵阳期中)研究发现,地表以下岩层的温度与它所处的深度有表中的关系:
岩层的深
度h/km 1 2 3 4 5 6 …
岩层的温
度t/℃ 55 90 125 160 195 230 …
根据以上信息,回答下列问题:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)岩层的深度h每增加1 km,温度t是怎样变化的?
(3)估计岩层10 km深处的温度是多少?
解:(1)上表反映了岩层的深度h(km)与岩层的温度t(℃)之间的关系;其中岩层深度h(km)是自变量,岩层的温度t(℃)是因变量
(2)岩层的深度h每增加1 km,温度t上升35 ℃,关系式:t=55+35(h-1)=35h+20
(3)当h=10 km时,t=35×10+20=370(℃)
9.根据科学研究表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)之间的关系如下表所示:下列说法不正确的是( )
x/kg 0 1 2 3 4 5
y/cm 20 20.5 21 21.5 22 22.5
B
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为0 cm
C.随着所挂物体的重量增加,弹簧长度逐渐变长
D.所挂物体的重量每增加1 kg,弹簧长度增加0.5 cm
10.(德阳期末)某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度(℃) -20 -10 0 10 20 30
声速(m/s) 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20 ℃时,声音5 s可以传播1740 m
D.当温度每升高10 ℃,声速增加6 m/s
C
11.随着我国人口增长速度的减慢,小学入学儿童数量有所减少,表中的数据近似地呈现了某地区入学儿童的变化趋势.
年份(x) 2016 2017 2018 …
入学儿童人数(y) 2520 2330 2140 …
(1)上表中________是自变量,________________是因变量;
(2)你预计该地区从______年起入学儿童的人数在1600人左右.
年份
入学儿童人数
2021
12. 如表是某报纸公布的世界人口数据情况:
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
年份 1957 1974 1987 1999 2010 2025
人口数 30亿 40亿 50亿 60亿 70亿 80亿
解:(1)表中有两个变量,分别是年份和人口数
(2)用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是增大
13.下表给出了橘农王林去年橘子的销售额(元)随橘子卖出质量(千克)的变化的有关数据:
卖出质量(千克) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是多少?
(3)估计当橘子卖出50千克时,销售额是多少?
解:(1)表中反映了橘子的卖出质量与销售额之间的关系,橘子的卖出质量是自变量,销售额是因变量
(2)当橘子卖出5千克时,销售额为10元
(3)当橘子卖出50千克时,销售额为100元
14.已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与铝用量有如下关系:
底面半径x(cm) 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量y(cm3) 6.9 6.0 5.6 5.5 5.7 6.0 6.5
(1)上表反映了易拉罐底面半径和用铝量两个变量之间的关系,哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4 cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由;
(4)粗略说一说易拉罐底面半径对所需铝质量的影响.
解:(1)易拉罐底面半径为自变量,用铝量为因变量
(2)当底面半径为2.4 cm时,易拉罐的用铝量为5.6 cm3
(3)易拉罐底面半径为2.8 cm时比较合适,∵此时用铝较少,成本低
(4)当易拉罐底面半径在1.6 cm~2.8 cm变化时,用铝量随半径的增大而减小,当易拉罐底面半径在2.8 cm~4.0 cm间变化时,用铝量随半径的增大而增大
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
