北师大版数学八年级下册 1.1 第1课时 等腰三角形的性质 课件(共14张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 1.1 第1课时 等腰三角形的性质 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 09:49:09 | ||
图片预览


文档简介
(共15张PPT)
第一章 三角形的证明
1.1 等腰三角形
第1课时 等腰三角形的性质
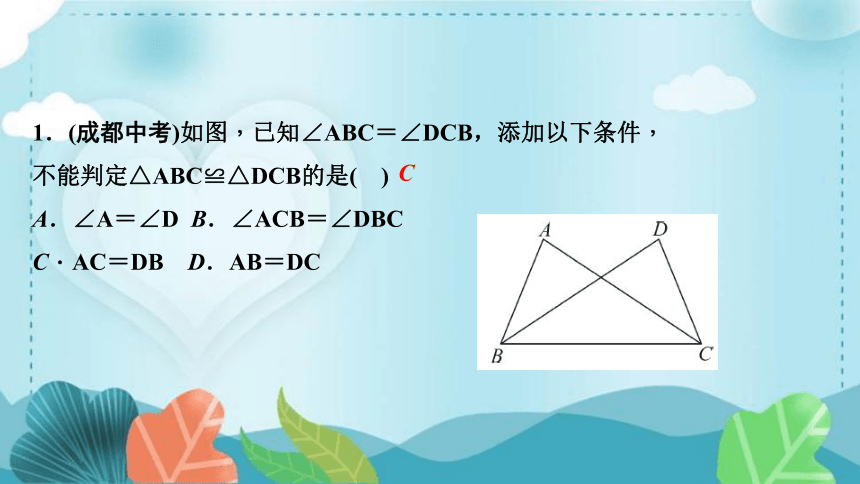
1.(成都中考)如图,已知∠ABC=∠DCB,添加以下条件,
不能判定△ABC≌△DCB的是( )
A.∠A=∠D B.∠ACB=∠DBC
C.AC=DB D.AB=DC
C
A
B
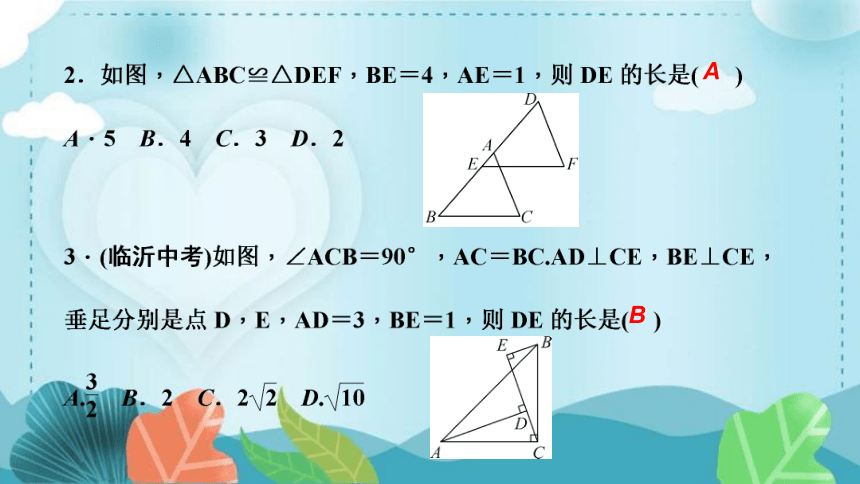
4.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
5.如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,
则∠ABD等于( )
A.36° B.54° C.18° D.64°
A
B
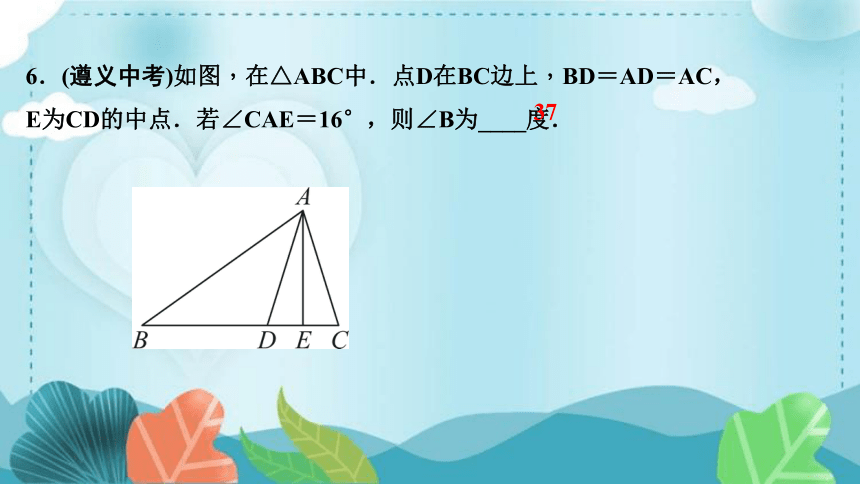
6.(遵义中考)如图,在△ABC中.点D在BC边上,BD=AD=AC,
E为CD的中点.若∠CAE=16°,则∠B为____度.
37
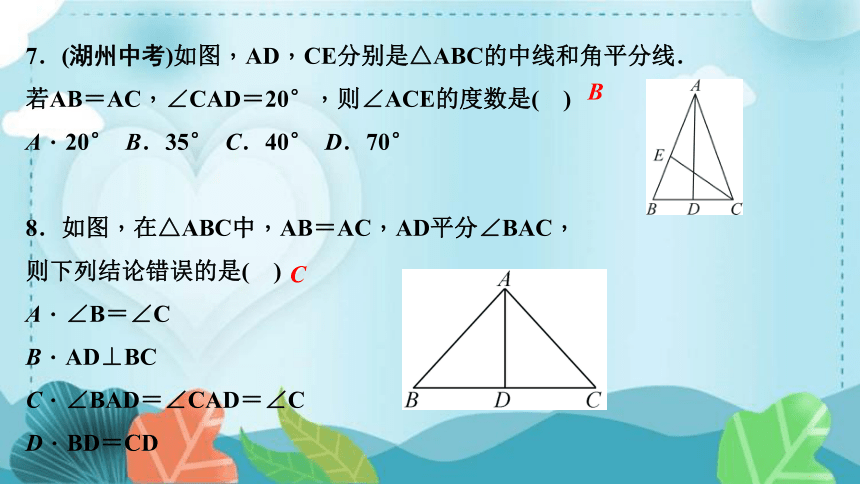
7.(湖州中考)如图,AD,CE分别是△ABC的中线和角平分线.
若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
8.如图,在△ABC中,AB=AC,AD平分∠BAC,
则下列结论错误的是( )
A.∠B=∠C
B.AD⊥BC
C.∠BAD=∠CAD=∠C
D.BD=CD
B
C
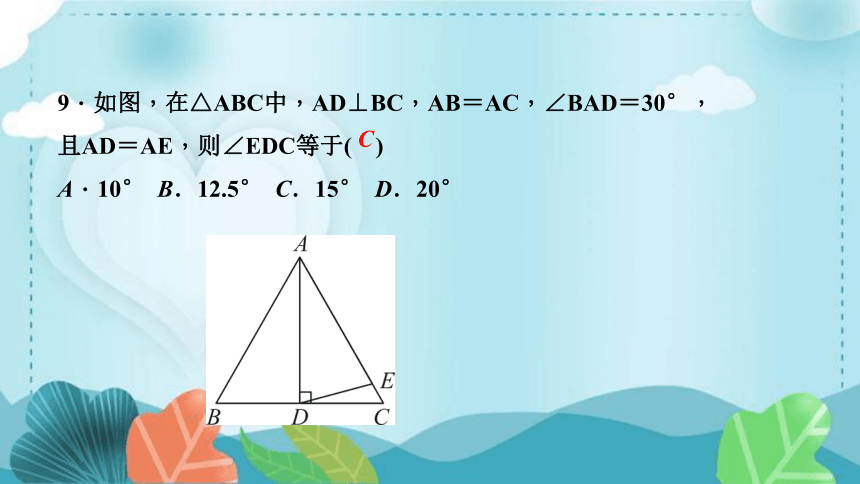
9.如图,在△ABC中,AD⊥BC,AB=AC,∠BAD=30°,
且AD=AE,则∠EDC等于( )
A.10° B.12.5° C.15° D.20°
C
10.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
11.如图,在△ABC中,D为AB上一点,E为BC上一点,
且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.50° B.51° C.51.5° D.52.5°
D
D
12.(娄底中考)如图,△ABC中,AB=AC,AD⊥BC于点D,
DE⊥AB于点E,BF⊥AC于点F,DE=3 cm,则BF=__ cm.
6
13.如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.
证明:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中,
AB=AC,∠B=∠C,BD=CE,∴△ABD≌△ACE(SAS),∴AD=AE
14.如图,在△ABC中,AB=AC,AD平分∠BAC,点M,N分别在边AB,AC上,AM=2MB,AN=2NC,求证:DM=DN.
15.(1)如图1,在Rt△ABC中,∠ACB=90°,点D,E在边AB上,
且AD=AC,BE=BC,求∠DCE的度数;
(2)如图2,在△ABC中,∠ACB=40°,点D,E在直线AB上,
且AD=AC,BE=BC,则∠DCE=________;
(3)在△ABC中,∠ACB=n°(0<n<180),点D,E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).
解:(1)∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2.∵∠A+∠B=90°,∴∠ACD+∠BCE=180°-(∠A+∠B)÷2=180°-45°=135°,∴∠DCE=∠ACD+∠BCE-∠ACB=135°-90°=45°
(2)110°
第一章 三角形的证明
1.1 等腰三角形
第1课时 等腰三角形的性质
1.(成都中考)如图,已知∠ABC=∠DCB,添加以下条件,
不能判定△ABC≌△DCB的是( )
A.∠A=∠D B.∠ACB=∠DBC
C.AC=DB D.AB=DC
C
A
B
4.如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
5.如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,
则∠ABD等于( )
A.36° B.54° C.18° D.64°
A
B
6.(遵义中考)如图,在△ABC中.点D在BC边上,BD=AD=AC,
E为CD的中点.若∠CAE=16°,则∠B为____度.
37
7.(湖州中考)如图,AD,CE分别是△ABC的中线和角平分线.
若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
8.如图,在△ABC中,AB=AC,AD平分∠BAC,
则下列结论错误的是( )
A.∠B=∠C
B.AD⊥BC
C.∠BAD=∠CAD=∠C
D.BD=CD
B
C
9.如图,在△ABC中,AD⊥BC,AB=AC,∠BAD=30°,
且AD=AE,则∠EDC等于( )
A.10° B.12.5° C.15° D.20°
C
10.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
11.如图,在△ABC中,D为AB上一点,E为BC上一点,
且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.50° B.51° C.51.5° D.52.5°
D
D
12.(娄底中考)如图,△ABC中,AB=AC,AD⊥BC于点D,
DE⊥AB于点E,BF⊥AC于点F,DE=3 cm,则BF=__ cm.
6
13.如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.
证明:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中,
AB=AC,∠B=∠C,BD=CE,∴△ABD≌△ACE(SAS),∴AD=AE
14.如图,在△ABC中,AB=AC,AD平分∠BAC,点M,N分别在边AB,AC上,AM=2MB,AN=2NC,求证:DM=DN.
15.(1)如图1,在Rt△ABC中,∠ACB=90°,点D,E在边AB上,
且AD=AC,BE=BC,求∠DCE的度数;
(2)如图2,在△ABC中,∠ACB=40°,点D,E在直线AB上,
且AD=AC,BE=BC,则∠DCE=________;
(3)在△ABC中,∠ACB=n°(0<n<180),点D,E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).
解:(1)∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2.∵∠A+∠B=90°,∴∠ACD+∠BCE=180°-(∠A+∠B)÷2=180°-45°=135°,∴∠DCE=∠ACD+∠BCE-∠ACB=135°-90°=45°
(2)110°
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
