六年级数学下册课件-7.2.6立体图形的表面积和体积(共88张PPT)苏教版
文档属性
| 名称 | 六年级数学下册课件-7.2.6立体图形的表面积和体积(共88张PPT)苏教版 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 11:02:16 | ||
图片预览







文档简介
(共88张PPT)
从数学的角度来看,你能解决哪些问题呢?
无锡市东北塘农坝小学 陆明
总复习
● 整理与反思
长方体
正方体
圆柱体
圆锥体
● 整理与反思
立体图形的
表面积和体积
表面积和体积的意义
表面积和体积的计量单位
表面积和体积的计算方法
课前复习
1.什么叫物体的表面积?什么叫物体的体积? 什么叫物体的容积?
2.常用的体积(容积)单位有哪些?相邻单位间进率各是多少?
3. 立体图形的表面积怎样计算?立体图形的体积怎样计算?
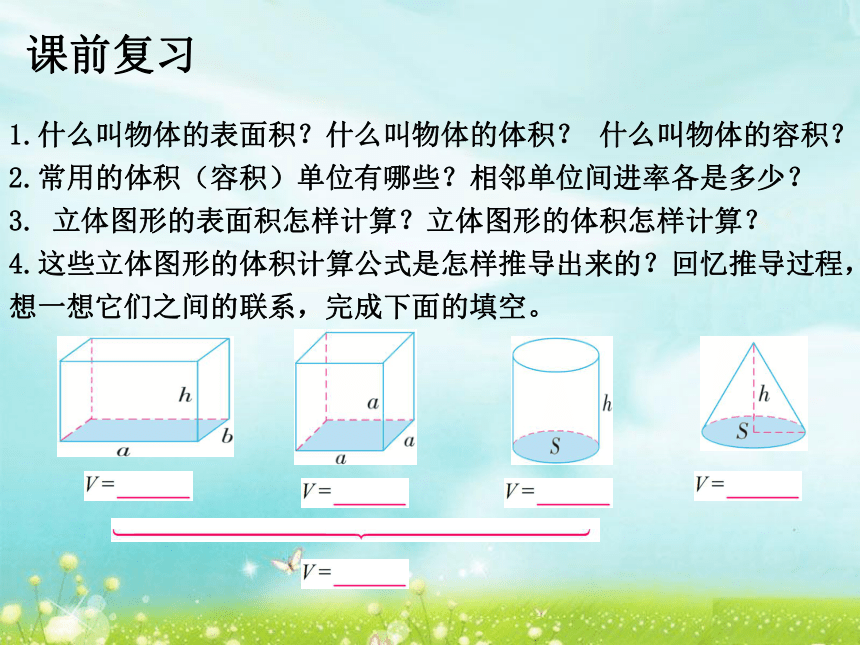
4.这些立体图形的体积计算公式是怎样推导出来的?回忆推导过程,想一想它们之间的联系,完成下面的填空。
● 整理与反思
立体图形的
表面积和体积
表面积和体积的意义
表面积和体积的计量单位
表面积和体积的计算方法
什么叫物体的表面积?什么叫物体的体积?什么叫容器的容积?
回忆一下:
6个面面积的和
6个面面积的和
3个面面积的和
2个面面积的和
表面积:是指物体表面所有面的面积总和。
体 积: 是指物体所占空间的大小。
容 积: 是指容器所能容纳物体的体积。
● 整理与反思
1. 选一选
要在一个长和宽都是30厘米,高是5分米长方体框架的外面糊上一层纸,就是求它的( );要在纸盒的四周贴上标签,就是求( );这个长方体的纸盒占有多大的空间,就是求纸盒的( )。这个长方体纸盒能装多少沙,是求纸盒的( )
A侧面积 B 棱长总和 C表面积 D体积 E容积
C
A
D
E
2. 判一判
一个圆柱形水桶的体积就是它的容积。( )
×
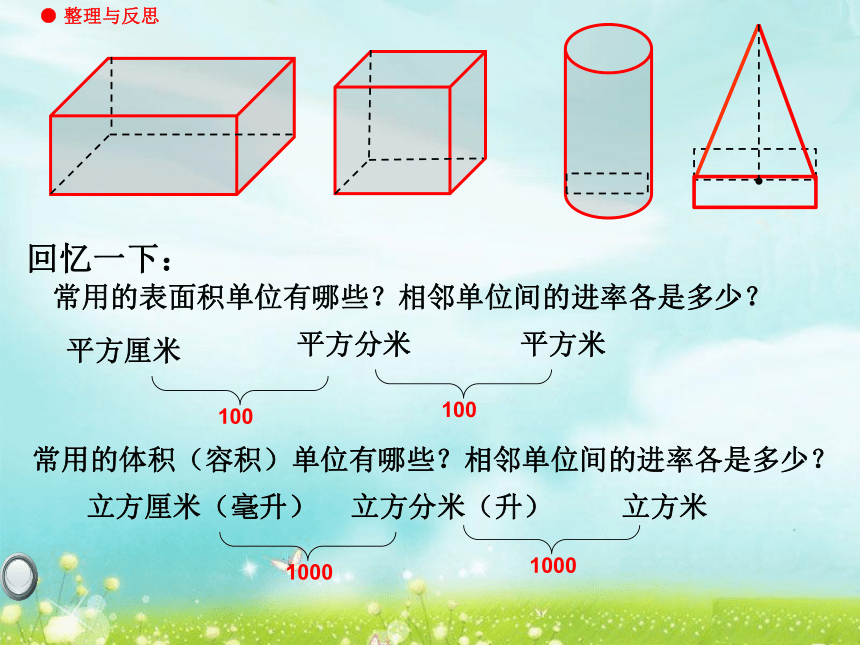
常用的体积(容积)单位有哪些?相邻单位间的进率各是多少?
回忆一下:
常用的表面积单位有哪些?相邻单位间的进率各是多少?
平方厘米
100
平方分米
平方米
100
立方厘米(毫升)
立方分米(升)
立方米
1000
1000
● 整理与反思
1. 小小判官。
小明家的房间很大,卧室地面的面积就有15立方米。( )
×
农坝小学六(1)班教室的空间大约是144平方米。( )
×
﹏
﹏
2. 在括号里填合适的单位。
(1)一间卧室地面的面积是 15( )。
平方米
(2)一瓶牛奶大约有 250( )。
(3)一间教室的空间大约是 144( )。
(4)一台微波炉的体积是 92( ),容积是25( )。
毫升
立方米
立方分米
升
3.
0.5 m3 =( )dm3 4050 dm3 =( )m3
0.09 dm3 =( )cm3 60 cm3 =( )dm3
1.04 L =( )mL 75 mL =( )cm3
500
4.05
90
0.06
1040
75
回忆一下:
立体图形的表面积怎样计算?
● 整理与反思
长方体的表面积 = (上 面 + 前 面 + 左 面 )×2
下面
前面
后面
左面
右面
上面
长
宽
高
=(长×宽+长×高+宽×高)×2
正方体的表面积=一个面的面积×6
棱长
棱长
棱长
=棱长×棱长×6
圆柱的表面积=侧面积+底面积×2
底面
底面
--------底面周长--------
高
=底面周长×高+底面积×2
侧面
a
b
h
a
a
a
h
r
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh) ×2
6a
2лrh
2лrh+ 2лr
2
2
● 立体图形的表面积
回忆一下:
立体图形的体积怎样计算?这些立体图形的体积计算公式是怎样推导出来的?
● 整理与反思
长方体的体积公式推导过程
棱长1厘米的正方体,体积是1立方厘米
4厘米
3厘米
2厘米
长方体的体积=长×宽×高
长方体的体积公式推导过程
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积 = 长 × 宽 × 高
棱长
棱长
棱长
棱长
棱长
棱长
正
正方体体积的推导过程
因为正方体是长、宽、高都相等的长方体,所以
圆柱体体积的推导过程
圆柱体体积的推导过程
拼成的长方体与原来的圆柱体比较,什么变了?什么没变?
圆柱体积
长方体体积
底面积
底面积
高
高
=
×
=
×
圆锥体体积的推导过程
圆锥体体积的推导过程
结论:圆柱体积是等底等高 圆锥体积的3倍 ,圆锥体积是等底等高圆柱体积的
圆锥的体积= × 底面积 ×高
正方体、长方体和圆柱的体积有什么相似的地方呢?
V=abh
V=a3
V=Sh
像长方体、正方体、圆柱这样上下两个面完全相同,而且上下粗细完全一样的立体图形叫做直柱体。
直柱体的体积 = 底面积×高
转化
实验、转化
推导体积计算公式
推导体积计算公式
主要利用转化的数学思想方法
小结
V = sh
a
b
h
a
a
s
h
s
h
V = a3
V = abh
a
V = sh
V = sh
1
3
3.计算下面立体图形的表面积和体积。
表面积:
42×6=96(平方厘米)
体积:
43 = 64(立方厘米)
3.计算下面立体图形的表面积和体积。
表面积:
(5×3+4×3+5×4)×2
=(15+12+20)×2
= 94(平方厘米)
体积:
5×4×3 = 60(立方厘米)
3.计算下面立体图形的表面积和体积。
表面积:
10×π×5=50π(平方厘米)
π×(10÷2)2×2=50π (平方厘米)
50π+50π=100π(平方厘米)
体积:
(10÷2)2 × π×5=125π(立方厘米)
4.求下面立体图形的体积。
(1)一个正方体,底面周长是 8 dm。
(2)一个长方体,底面是边长12cm 的正方形,高是50cm。
(8÷4)3= 8(立方分米)
答:正方体的体积是8立方分米。
12×12×50 = 7200(立方厘米)
答:长方体的体积是7200立方厘米。
4.求下面立体图形的体积。
(3)一个圆柱,底面周长是 12.56 cm,高是 5 cm。
(4)一个圆锥,底面半径是 3 cm,高是 4.5 cm。
12.56÷3.14÷2 =2(厘米)
22×π×5=20π(立方厘米)
答:圆柱的体积是20π立方厘米。
32×π×4.5× =13.5π(立方厘米)
答:圆锥的体积是13.5π立方厘米。
量得它的长是7厘米,宽是4厘米,高是9厘米。
①制作这个长方体盒子需要多少平方厘米材料?(接头处忽略不计)
②这种牛奶盒上标注牛奶的净含量为250毫升,这个牛奶盒真的可以装250毫升吗?(牛奶盒厚度忽略不计)
(7×4+7×9+4×9)×2
=127×2
=254(平方厘米)
7×4×9=252(立方厘米)=252毫升
252毫升>250毫升
净含量:250ml
立体图形 表面积 体积
意 义
计量单位
------
● 整理与反思
(ab+ah +bh) ×2
S=
2
6a
S=
2
2∏r
+
Ch
S=
V=abh
V=a
3
V=∏r h
2
V=Sh
V= ∏r h
2
1
3
V= Sh
1
3
……
2
cm
2
dm
2
m
……
3
cm
3
dm
3
m
物体所占空间的大小。
物体所有面的面积总和。
计算方法
长方体
正方体
圆 柱
圆 锥
● 练习与实践
闯关大挑战
判断:一个长、宽、高分别是10厘米、8厘米、7厘米的长方体可以从边长8.5厘米的正方形洞中漏下去。( )
● 练习与实践----挑战第一关:长方体、正方体
判断:一个长、宽、高分别是10厘米、8厘米、7厘米的长方体可以从边长8.5厘米的正方形洞中漏下去。( )
√
● 练习与实践----挑战第一关:长方体、正方体
● 练习与实践----挑战第一关:长方体与正方体
判断:一个长、宽、高分别是10厘米、8厘米、7厘米的长方体可以从边长8.5厘米的正方形洞中漏下去。( )
√
8cm
7cm
10cm
8.5cm
● 练习与实践----挑战第二关:圆柱与长方体
如图所示,把底面直径6厘米,高10厘米的圆柱切成若干等份,拼成一个近似的长方体。(只列式不计算)
这个长方体的表面积是: ,
体积是: 。
● 练习与实践----挑战第三关:圆锥与正方体
一个棱长是4分米正方体容器装满水后,
倒入一个底面积是12平方分米的圆锥体容器里正好装满,
这个圆锥体的高是多少分米?
4×4×4=64(立方分米)
64×3÷12=16(分米)
● 练习与实践——挑战第四关:立体图形的切分
将一个直径是6厘米的圆锥沿高切开,切面是一个等腰直角三角形,那么这个圆锥的体积是( )。
底面直径
圆锥的高
。
45
● 练习与实践——挑战第四关:立体图形的切分
将一个直径是6厘米的圆锥沿高切开,切面是一个等腰直角三角形,那么这个圆锥的体积是( )。
底面直径
圆锥的高
。
45
9π立方厘米
● 练习与实践——挑战第五关:立体图形的切分
一个长方体正好可以切成3个一样的正方体,切开后每个正方体的表面积是12平方厘米,那么原来长方体的表面积( )
平方厘米。
● 练习与实践——挑战第五关:立体图形的切分
一个长方体正好可以切成3个一样的正方体,切开后每个正方体的表面积是12平方厘米,那么原来长方体的表面积( )
平方厘米。
12÷6=2(厘米)
(3×4+2)×2=28(平方厘米)
28
● 练习与实践——挑战第六关:立体图形的设计(课后研究)
用一个长14厘米、宽10厘米的硬纸板做成一个无盖的长方体纸盒,要求体积大于100立方厘米。画出示意图,并计算出体积。(街头处忽略不计)
从数学的角度来看,你能解决哪些问题呢?
无锡市东北塘农坝小学 陆明
总复习
● 整理与反思
长方体
正方体
圆柱体
圆锥体
● 整理与反思
立体图形的
表面积和体积
表面积和体积的意义
表面积和体积的计量单位
表面积和体积的计算方法
课前复习
1.什么叫物体的表面积?什么叫物体的体积? 什么叫物体的容积?
2.常用的体积(容积)单位有哪些?相邻单位间进率各是多少?
3. 立体图形的表面积怎样计算?立体图形的体积怎样计算?
4.这些立体图形的体积计算公式是怎样推导出来的?回忆推导过程,想一想它们之间的联系,完成下面的填空。
● 整理与反思
立体图形的
表面积和体积
表面积和体积的意义
表面积和体积的计量单位
表面积和体积的计算方法
什么叫物体的表面积?什么叫物体的体积?什么叫容器的容积?
回忆一下:
6个面面积的和
6个面面积的和
3个面面积的和
2个面面积的和
表面积:是指物体表面所有面的面积总和。
体 积: 是指物体所占空间的大小。
容 积: 是指容器所能容纳物体的体积。
● 整理与反思
1. 选一选
要在一个长和宽都是30厘米,高是5分米长方体框架的外面糊上一层纸,就是求它的( );要在纸盒的四周贴上标签,就是求( );这个长方体的纸盒占有多大的空间,就是求纸盒的( )。这个长方体纸盒能装多少沙,是求纸盒的( )
A侧面积 B 棱长总和 C表面积 D体积 E容积
C
A
D
E
2. 判一判
一个圆柱形水桶的体积就是它的容积。( )
×
常用的体积(容积)单位有哪些?相邻单位间的进率各是多少?
回忆一下:
常用的表面积单位有哪些?相邻单位间的进率各是多少?
平方厘米
100
平方分米
平方米
100
立方厘米(毫升)
立方分米(升)
立方米
1000
1000
● 整理与反思
1. 小小判官。
小明家的房间很大,卧室地面的面积就有15立方米。( )
×
农坝小学六(1)班教室的空间大约是144平方米。( )
×
﹏
﹏
2. 在括号里填合适的单位。
(1)一间卧室地面的面积是 15( )。
平方米
(2)一瓶牛奶大约有 250( )。
(3)一间教室的空间大约是 144( )。
(4)一台微波炉的体积是 92( ),容积是25( )。
毫升
立方米
立方分米
升
3.
0.5 m3 =( )dm3 4050 dm3 =( )m3
0.09 dm3 =( )cm3 60 cm3 =( )dm3
1.04 L =( )mL 75 mL =( )cm3
500
4.05
90
0.06
1040
75
回忆一下:
立体图形的表面积怎样计算?
● 整理与反思
长方体的表面积 = (上 面 + 前 面 + 左 面 )×2
下面
前面
后面
左面
右面
上面
长
宽
高
=(长×宽+长×高+宽×高)×2
正方体的表面积=一个面的面积×6
棱长
棱长
棱长
=棱长×棱长×6
圆柱的表面积=侧面积+底面积×2
底面
底面
--------底面周长--------
高
=底面周长×高+底面积×2
侧面
a
b
h
a
a
a
h
r
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh) ×2
6a
2лrh
2лrh+ 2лr
2
2
● 立体图形的表面积
回忆一下:
立体图形的体积怎样计算?这些立体图形的体积计算公式是怎样推导出来的?
● 整理与反思
长方体的体积公式推导过程
棱长1厘米的正方体,体积是1立方厘米
4厘米
3厘米
2厘米
长方体的体积=长×宽×高
长方体的体积公式推导过程
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积 = 长 × 宽 × 高
棱长
棱长
棱长
棱长
棱长
棱长
正
正方体体积的推导过程
因为正方体是长、宽、高都相等的长方体,所以
圆柱体体积的推导过程
圆柱体体积的推导过程
拼成的长方体与原来的圆柱体比较,什么变了?什么没变?
圆柱体积
长方体体积
底面积
底面积
高
高
=
×
=
×
圆锥体体积的推导过程
圆锥体体积的推导过程
结论:圆柱体积是等底等高 圆锥体积的3倍 ,圆锥体积是等底等高圆柱体积的
圆锥的体积= × 底面积 ×高
正方体、长方体和圆柱的体积有什么相似的地方呢?
V=abh
V=a3
V=Sh
像长方体、正方体、圆柱这样上下两个面完全相同,而且上下粗细完全一样的立体图形叫做直柱体。
直柱体的体积 = 底面积×高
转化
实验、转化
推导体积计算公式
推导体积计算公式
主要利用转化的数学思想方法
小结
V = sh
a
b
h
a
a
s
h
s
h
V = a3
V = abh
a
V = sh
V = sh
1
3
3.计算下面立体图形的表面积和体积。
表面积:
42×6=96(平方厘米)
体积:
43 = 64(立方厘米)
3.计算下面立体图形的表面积和体积。
表面积:
(5×3+4×3+5×4)×2
=(15+12+20)×2
= 94(平方厘米)
体积:
5×4×3 = 60(立方厘米)
3.计算下面立体图形的表面积和体积。
表面积:
10×π×5=50π(平方厘米)
π×(10÷2)2×2=50π (平方厘米)
50π+50π=100π(平方厘米)
体积:
(10÷2)2 × π×5=125π(立方厘米)
4.求下面立体图形的体积。
(1)一个正方体,底面周长是 8 dm。
(2)一个长方体,底面是边长12cm 的正方形,高是50cm。
(8÷4)3= 8(立方分米)
答:正方体的体积是8立方分米。
12×12×50 = 7200(立方厘米)
答:长方体的体积是7200立方厘米。
4.求下面立体图形的体积。
(3)一个圆柱,底面周长是 12.56 cm,高是 5 cm。
(4)一个圆锥,底面半径是 3 cm,高是 4.5 cm。
12.56÷3.14÷2 =2(厘米)
22×π×5=20π(立方厘米)
答:圆柱的体积是20π立方厘米。
32×π×4.5× =13.5π(立方厘米)
答:圆锥的体积是13.5π立方厘米。
量得它的长是7厘米,宽是4厘米,高是9厘米。
①制作这个长方体盒子需要多少平方厘米材料?(接头处忽略不计)
②这种牛奶盒上标注牛奶的净含量为250毫升,这个牛奶盒真的可以装250毫升吗?(牛奶盒厚度忽略不计)
(7×4+7×9+4×9)×2
=127×2
=254(平方厘米)
7×4×9=252(立方厘米)=252毫升
252毫升>250毫升
净含量:250ml
立体图形 表面积 体积
意 义
计量单位
------
● 整理与反思
(ab+ah +bh) ×2
S=
2
6a
S=
2
2∏r
+
Ch
S=
V=abh
V=a
3
V=∏r h
2
V=Sh
V= ∏r h
2
1
3
V= Sh
1
3
……
2
cm
2
dm
2
m
……
3
cm
3
dm
3
m
物体所占空间的大小。
物体所有面的面积总和。
计算方法
长方体
正方体
圆 柱
圆 锥
● 练习与实践
闯关大挑战
判断:一个长、宽、高分别是10厘米、8厘米、7厘米的长方体可以从边长8.5厘米的正方形洞中漏下去。( )
● 练习与实践----挑战第一关:长方体、正方体
判断:一个长、宽、高分别是10厘米、8厘米、7厘米的长方体可以从边长8.5厘米的正方形洞中漏下去。( )
√
● 练习与实践----挑战第一关:长方体、正方体
● 练习与实践----挑战第一关:长方体与正方体
判断:一个长、宽、高分别是10厘米、8厘米、7厘米的长方体可以从边长8.5厘米的正方形洞中漏下去。( )
√
8cm
7cm
10cm
8.5cm
● 练习与实践----挑战第二关:圆柱与长方体
如图所示,把底面直径6厘米,高10厘米的圆柱切成若干等份,拼成一个近似的长方体。(只列式不计算)
这个长方体的表面积是: ,
体积是: 。
● 练习与实践----挑战第三关:圆锥与正方体
一个棱长是4分米正方体容器装满水后,
倒入一个底面积是12平方分米的圆锥体容器里正好装满,
这个圆锥体的高是多少分米?
4×4×4=64(立方分米)
64×3÷12=16(分米)
● 练习与实践——挑战第四关:立体图形的切分
将一个直径是6厘米的圆锥沿高切开,切面是一个等腰直角三角形,那么这个圆锥的体积是( )。
底面直径
圆锥的高
。
45
● 练习与实践——挑战第四关:立体图形的切分
将一个直径是6厘米的圆锥沿高切开,切面是一个等腰直角三角形,那么这个圆锥的体积是( )。
底面直径
圆锥的高
。
45
9π立方厘米
● 练习与实践——挑战第五关:立体图形的切分
一个长方体正好可以切成3个一样的正方体,切开后每个正方体的表面积是12平方厘米,那么原来长方体的表面积( )
平方厘米。
● 练习与实践——挑战第五关:立体图形的切分
一个长方体正好可以切成3个一样的正方体,切开后每个正方体的表面积是12平方厘米,那么原来长方体的表面积( )
平方厘米。
12÷6=2(厘米)
(3×4+2)×2=28(平方厘米)
28
● 练习与实践——挑战第六关:立体图形的设计(课后研究)
用一个长14厘米、宽10厘米的硬纸板做成一个无盖的长方体纸盒,要求体积大于100立方厘米。画出示意图,并计算出体积。(街头处忽略不计)
