9.4.1 利用角的关系判定三角形相似同步练习(含答案)
文档属性
| 名称 | 9.4.1 利用角的关系判定三角形相似同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 14:27:21 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第1课时 利用角的关系判定三角形相似
知识梳理
1.根据相似多边形的定义,三角分别_________、三边_________的两个三角形叫做相似三角形.
2.定理:两角分别___________的两个三角形相似.
基础练习
1.在△ABC和△A′B′C′中,∠A=58°,∠B=50°, 则这两个三角形( )
A.相似且全等 B.相似 C.全等 D.无法判定
2.如图,△ABC与△BDE都是等边三角形,点D在边AC上(不与点A,C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
3.如图,在△ABC中,P为边AB上一点,有下列条件:①∠ACP=∠B;②∠APC=∠ACB;③∠CAP=∠BAC.其中,能确定△APC和△ACB相似的是__________(填序号).
第3题图 第4题图
4.如图,BE,CD相交于点O,且△1=《2,则图中的相似三角形是_____.
5.如图,在△ABC中,四边形DBFE是平行四边形,求证:△ADE∽△EFC.
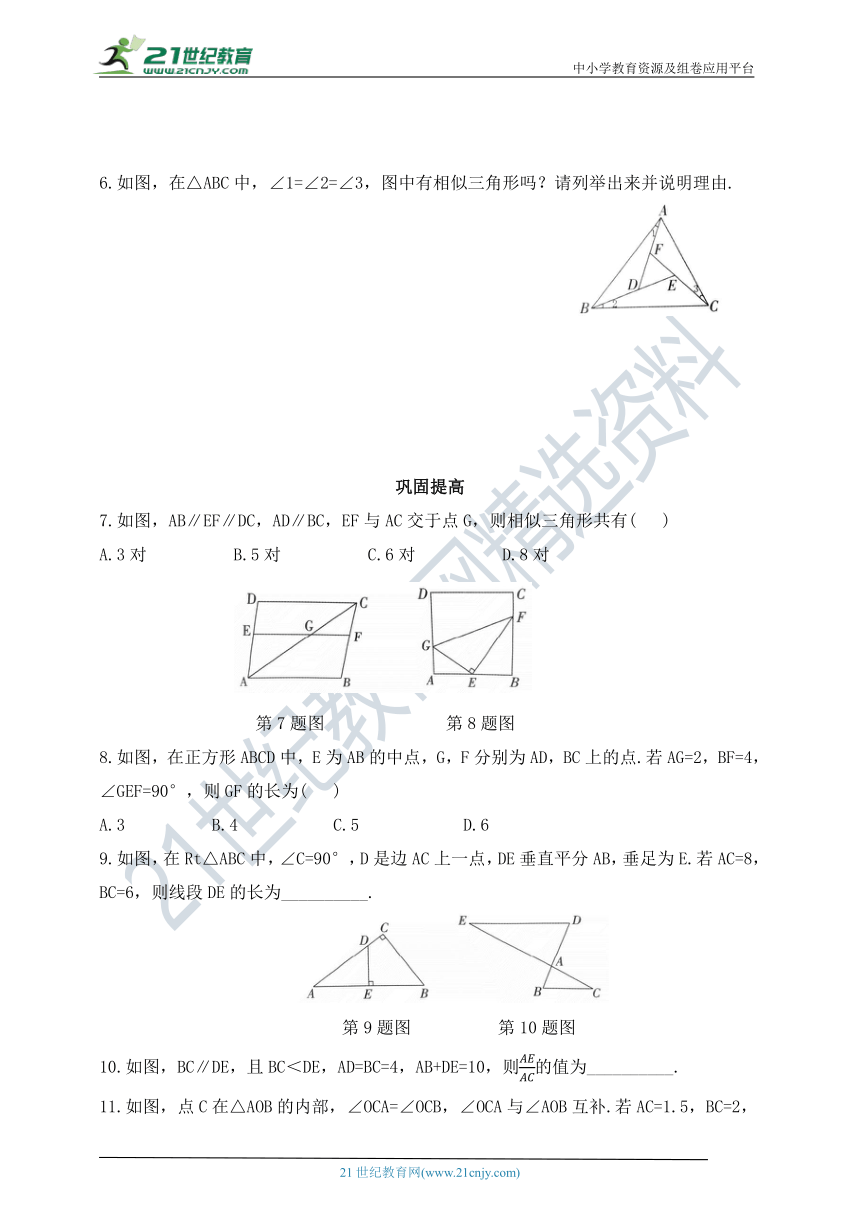
6.如图,在△ABC中,∠1=∠2=∠3,图中有相似三角形吗?请列举出来并说明理由.
巩固提高
7.如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( )
A.3对 B.5对 C.6对 D.8对
第7题图 第8题图
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD,BC上的点.若AG=2,BF=4,∠GEF=90°,则GF的长为( )
A.3 B.4 C.5 D.6
9.如图,在Rt△ABC中,∠C=90°,D是边AC上一点,DE垂直平分AB,垂足为E.若AC=8,BC=6,则线段DE的长为__________.
第9题图 第10题图
10.如图,BC∥DE,且BC<DE,AD=BC=4,AB+DE=10,则的值为__________.
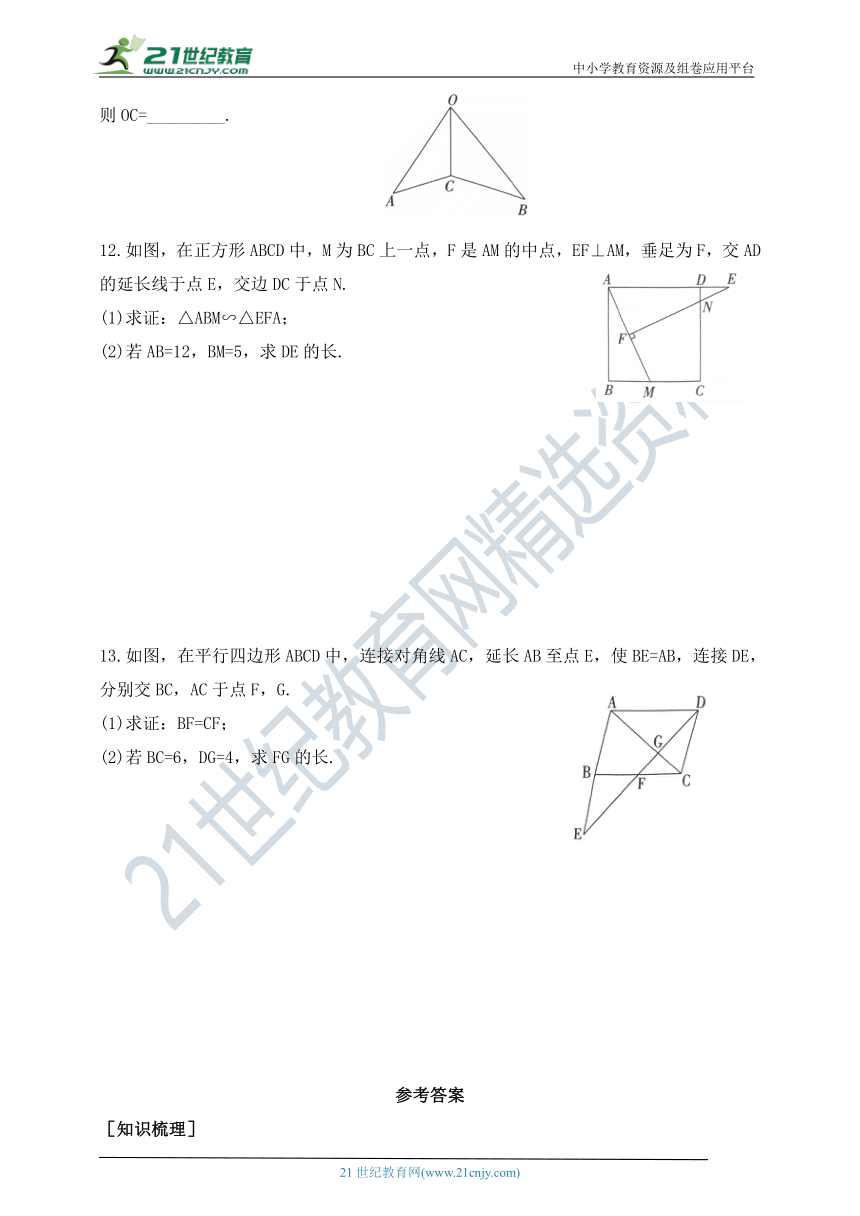
11.如图,点C在△AOB的内部,∠OCA=∠OCB,∠OCA与∠AOB互补.若AC=1.5,BC=2,则OC=_________.
12.如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交边DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
13.如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长.
参考答案
[知识梳理]
1.相等 成比例 2.相等
[基础练习]
1.B 2.C 3.①② 4.△DOE∽△BOC,△ACD∽△AEB
5.∵四边形DBFE是平行四边形,∴DE∥BC,EF∥AB.
∴∠AED=∠C,∠CEF=∠A.∴△ADE∽△EFC.
6.有,△DEF∽△BCA理由:∵∠CFD=∠3+∠FAC,∠BAC=∠1+∠FAC,又∵∠1=∠3,
∴∠CFD=△BAC.同理,可得∠FED=∠ACB.∴△DEF∽△BCA.
[巩固提高]
7.C 8.D 9. 10.2 11.
12.(1)∵四边形ABCD是正方形,∴AB=AD,∠B=90°,AD∥BC.∴∠AMB=∠EAF.又∵EF⊥AM,∴∠AFE=90°.∴∠B=∠AFE.∴△ABM∽△EFA.
(2)∵∠B=90°,AB=12,BM=5,∴
∵F是AM的中点,∴=6.5.∵△ABM∽△EFA,∴ 即 ∴AE=16.9.∴DE=AE-AD=16.9-12=4.9.
13.(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴易得△EBF∽△EAD.∴ ∴BF= .
(2)∵四边形ABCD是平行四边形,∴AD∥CF.∴易得△FGC∽△DGA.∴ 即 ∴FG=2 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第1课时 利用角的关系判定三角形相似
知识梳理
1.根据相似多边形的定义,三角分别_________、三边_________的两个三角形叫做相似三角形.
2.定理:两角分别___________的两个三角形相似.
基础练习
1.在△ABC和△A′B′C′中,∠A=58°,∠B=50°, 则这两个三角形( )
A.相似且全等 B.相似 C.全等 D.无法判定
2.如图,△ABC与△BDE都是等边三角形,点D在边AC上(不与点A,C重合),DE与AB相交于点F,那么与△BFD相似的三角形是( )
A.△BFE B.△BDC C.△BDA D.△AFD
3.如图,在△ABC中,P为边AB上一点,有下列条件:①∠ACP=∠B;②∠APC=∠ACB;③∠CAP=∠BAC.其中,能确定△APC和△ACB相似的是__________(填序号).
第3题图 第4题图
4.如图,BE,CD相交于点O,且△1=《2,则图中的相似三角形是_____.
5.如图,在△ABC中,四边形DBFE是平行四边形,求证:△ADE∽△EFC.
6.如图,在△ABC中,∠1=∠2=∠3,图中有相似三角形吗?请列举出来并说明理由.
巩固提高
7.如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则相似三角形共有( )
A.3对 B.5对 C.6对 D.8对
第7题图 第8题图
8.如图,在正方形ABCD中,E为AB的中点,G,F分别为AD,BC上的点.若AG=2,BF=4,∠GEF=90°,则GF的长为( )
A.3 B.4 C.5 D.6
9.如图,在Rt△ABC中,∠C=90°,D是边AC上一点,DE垂直平分AB,垂足为E.若AC=8,BC=6,则线段DE的长为__________.
第9题图 第10题图
10.如图,BC∥DE,且BC<DE,AD=BC=4,AB+DE=10,则的值为__________.
11.如图,点C在△AOB的内部,∠OCA=∠OCB,∠OCA与∠AOB互补.若AC=1.5,BC=2,则OC=_________.
12.如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交边DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
13.如图,在平行四边形ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长.
参考答案
[知识梳理]
1.相等 成比例 2.相等
[基础练习]
1.B 2.C 3.①② 4.△DOE∽△BOC,△ACD∽△AEB
5.∵四边形DBFE是平行四边形,∴DE∥BC,EF∥AB.
∴∠AED=∠C,∠CEF=∠A.∴△ADE∽△EFC.
6.有,△DEF∽△BCA理由:∵∠CFD=∠3+∠FAC,∠BAC=∠1+∠FAC,又∵∠1=∠3,
∴∠CFD=△BAC.同理,可得∠FED=∠ACB.∴△DEF∽△BCA.
[巩固提高]
7.C 8.D 9. 10.2 11.
12.(1)∵四边形ABCD是正方形,∴AB=AD,∠B=90°,AD∥BC.∴∠AMB=∠EAF.又∵EF⊥AM,∴∠AFE=90°.∴∠B=∠AFE.∴△ABM∽△EFA.
(2)∵∠B=90°,AB=12,BM=5,∴
∵F是AM的中点,∴=6.5.∵△ABM∽△EFA,∴ 即 ∴AE=16.9.∴DE=AE-AD=16.9-12=4.9.
13.(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴易得△EBF∽△EAD.∴ ∴BF= .
(2)∵四边形ABCD是平行四边形,∴AD∥CF.∴易得△FGC∽△DGA.∴ 即 ∴FG=2 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
