北师大版九年级数学上册 第2章一元二次方程评估卷(word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册 第2章一元二次方程评估卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 156.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 12:41:53 | ||
图片预览




文档简介
北师大版九年级数学上册 第2章 学情评估卷
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、选择题(每小题3分,共30分)
1.下列方程中,是一元二次方程的是( )
A.2x+3y-5=0 B.x2+=1
C.x2-1=0 D.ax2+bx+c=0
2.已知一元二次方程x2+kx+3=0的一个根为3,则k的值为( )
A.-4 B.4
C.-2 D.2
3.用配方法解方程x2+4x-5=0时,原方程应变形为( )
A.(x-2)2=1 B.(x-4)2=11
C.(x+2)2=9 D.(x+4)2=21
4.关于x的一元二次方程-kx2-6x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k>-3 B.k<3
C.k<3且k≠0 D.k>-3且k≠0
5.若对于任意实数a,b,c,d,定义=ad-bc,按照定义,若=0,则x的值为( )
A. B.-
C.3 D.±
6.某种商品经过两次涨价,每件零售价由200元涨至242元,求平均每次涨价的百分率.设平均每次涨价的百分率为x,则可列方程为( )
A.200(1+x)2=242 B.242(1-x)2=200
C.242(1-2x)=200 D.200(1+2x)=242
7.在△ABC中,AB=AC,BC=8,AB的长是方程x2-9x+20=0的一个根,则△ABC的周长为( )
A.16 B.16或18
C.17 D.18
8.已知x1,x2是一元二次方程x2-x-2=0的两个根,则+的值是( )
A.1 B.
C.-1 D.-
9.若直角三角形的两边长分别是方程x2-7x+12=0的两根,则该直角三角形的面积是( )
A.6 B.12
C.12或 D.6或
10.若m,n是方程x2-x-2 022=0的两个根,则代数式(m2-2m-2 022)(-n2+2n+2 022)的值为( )
A.2 023 B.2 022
C.2 021 D.2 020
二、填空题(每小题4分,共28分)
11.若关于x的方程xm+1-3=0是一元二次方程,则m=________.
12.若关于x的方程x2=a-1有实数根,则a的取值范围为________.
13.方程(x+3)2=x+3的根是____________.
14.若关于x的一元二次方程(k-1)x2+2kx+k+3=0有实数根,则k的取值范围是____________.
15.菱形的一条对角线长为8,其边长是方程x2-8x+15=0的一个根,则该菱形的面积为________.
16.若正数a是一元二次方程x2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,则a的值是________.
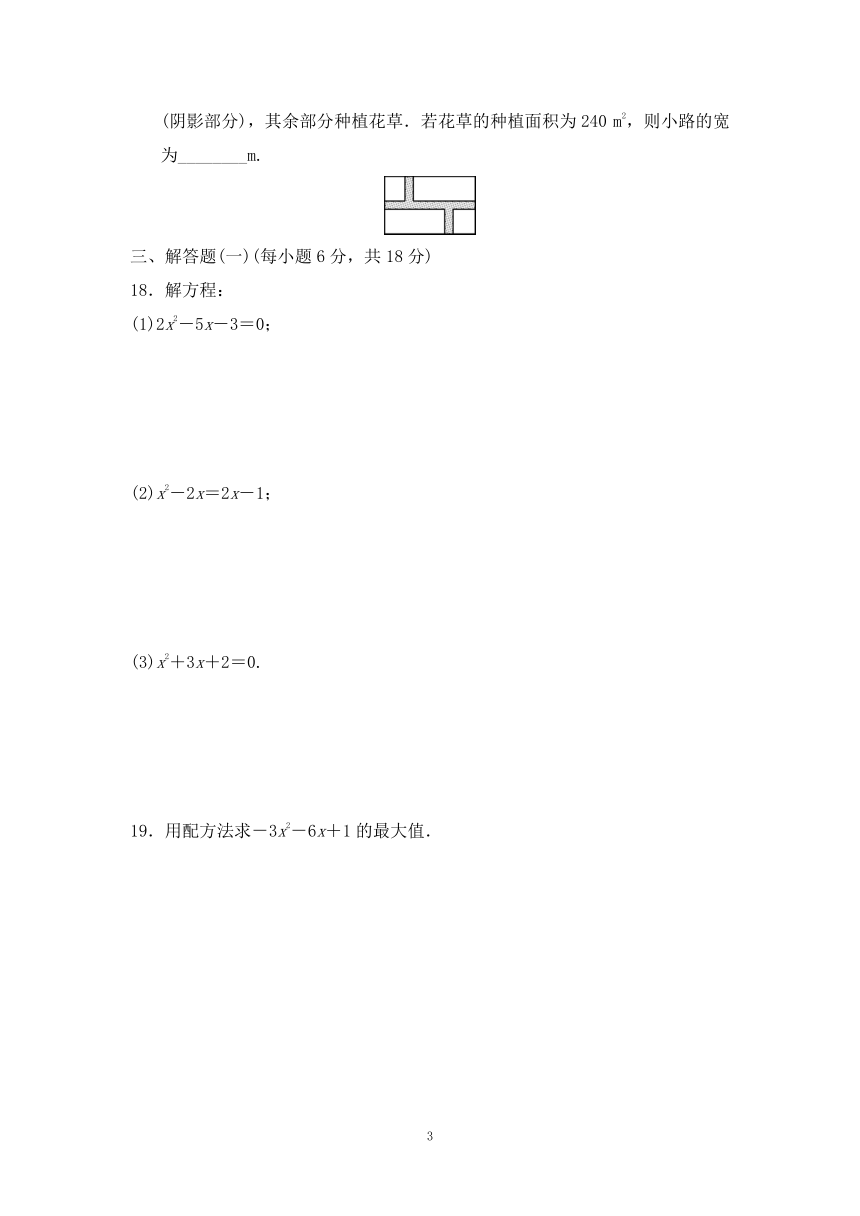
17.如图,在一块长为22 m,宽为14 m的矩形空地内修建三条宽度相等的小路(阴影部分),其余部分种植花草.若花草的种植面积为240 m2,则小路的宽为________m.
INCLUDEPICTURE"二改+1.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\二改+1.tif" \* MERGEFORMATINET
三、解答题(一)(每小题6分,共18分)
18.解方程:
(1)2x2-5x-3=0;
(2)x2-2x=2x-1;
(3)x2+3x+2=0.
19.用配方法求-3x2-6x+1的最大值.
20.已知关于x的一元二次方程x2-2 x+m=0有两个不相等的实数根,求实数m的最大整数值.
四、解答题(二)(每小题8分,共24分)
21.有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25,-16,第一次按键后,A,B两区分别显示25+a2,-16-3a.
(1)从初始状态按2次后,分别求A,B两区显示的结果;
(2)从初始状态按4次后,得A,B两区显示的代数式的和为1,求a的值.
22.关于x的一元二次方程x2-(k-3)x-2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程的两根分别为x1,x2,且x1+x2+x1x2=2,求k的值.
23.为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子产品的固定成本为100元,这种电子产品降价后的销售单价为多少元时,公司每天可获利32 000元?
五、解答题(三)(每小题10分,共20分)
24.如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门.
(1)若a=12,当矩形鸡舍的边长分别为多少时,鸡舍的面积为80平方米?
(2)当a的值在什么范围时,(1)中的解有两个?一个?无解?
(3)若墙的长度足够长,鸡舍的面积能否为90平方米?
INCLUDEPICTURE"初排+13.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+13.tif" \* MERGEFORMATINET
25.请阅读下列材料.
问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程的根的2倍.
解:设所求方程的根为y,则y=2x,所以x=.
把x=代入已知方程,得+-1=0.
化简,得y2+2y-4=0.
故所求方程为y2+2y-4=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程的根的相反数;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程的根的倒数.
答案
一、1.C 2.A 3.C 4.D 5.D 6.A 7.D
8.D 9.D 10.B
二、11.1 12.a≥1 13.x1=-3,x2=-2
14.k≤且k≠1 15.24 16.5 17.2
三、18.解:(1)∵a=2,b=-5,c=-3,
∴b2-4ac=(-5)2-4×2×(-3)=49>0,
∴x==,∴x1=-,x2=3.
(2)移项,得x2-4x=-1.
配方,得x2-4x+4=-1+4,
即(x-2)2=3.
两边开平方,得x-2=±,
即x-2=或x-2=-.
∴x1=2+,x2=2-.
(3)原方程可变形为(x+1)(x+2)=0,
∴x+1=0或x+2=0.∴x1=-1,x2=-2.
19.解:-3x2-6x+1
=-3(x2+2x)+1
=-3(x2+2x+1-1)+1
=-3(x+1)2+4,
∵-3(x+1)2≤0,∴-3(x+1)2+4≤4,
∴-3x2-6x+1的最大值为4.
20.解:∵一元二次方程x2-2 x+m=0有两个不相等的实数根,∴Δ=8-4m>0,解得m<2.
∴实数m的最大整数值为1.
四、21.解:(1)25+a2+a2=25+2a2,
-16-3a-3a=-16-6a.
答:A区显示的结果为(25+2a2),B区显示的结果为(-16-6a).
(2)依题意,得25+4a2+(-16-12a)=1,
化简,得a2-3a+2=0,解得a1=2,a2=1.
答:a的值为2或1.
22.(1)证明:∵b2-4ac=[-(k-3)]2-4×1×(-2k+2)=k2+2k+1=(k+1)2≥0,
∴方程总有两个实数根.
(2)解:由根与系数的关系,得x1+x2=k-3,x1x2=-2k+2,
∴x1+x2+x1x2=(k-3)+(-2k+2)=2,解得k=-3.
23.解:设降价后的销售单价为x元,则降价后每天可售出[300+5(200-x)]个,
依题意,得(x-100)[300+5(200-x)]=32 000,
整理,得x2-360x+32 400=0,
解得x1=x2=180.
180<200,符合题意.
答:这种电子产品降价后的销售单价为180元时,公司每天可获利32 000元.
五、24.解:(1)设矩形鸡舍垂直于墙的一边长为x米,则平行于墙的一边长为(26-2x)米.
依题意,得x(26-2x)=80,
解得x1=5,x2=8.
当x=5时,26-2x=16>12(舍去),
当x=8时,26-2x=10<12.
答:当矩形鸡舍的长为10米,宽为8米时,鸡舍的面积为80平方米.
(2)由(1)知,平行于墙的一边长为10米或16米,
∴当a≥16时,(1)中的解有两个,
当10≤a<16时,(1)中的解有一个,
当0<a<10时,(1)无解.
(3)由题意,得x(26-2x)=90,
整理,得x2-13x+45=0,
则Δ=b2-4ac=169-180=-11<0,
故鸡舍的面积不能为90平方米.
25.解:(1)设所求方程的根为z,
则z=-x,所以x=-z.
把x=-z代入已知方程,得z2-z-2=0,
故所求方程为z2-z-2=0.
(2)设所求方程的根为t,
则t=(x≠0),所以x=(t≠0).
把x=代入方程ax2+bx+c=0,
得a+b·+c=0.
去分母,得a+bt+ct2=0.
若c=0,则有ax2+bx=0,所以方程ax2+bx+c=0有一个根为0,不符合题意,所以c≠0.
故所求方程为ct2+bt+a=0(c≠0).
PAGE
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、选择题(每小题3分,共30分)
1.下列方程中,是一元二次方程的是( )
A.2x+3y-5=0 B.x2+=1
C.x2-1=0 D.ax2+bx+c=0
2.已知一元二次方程x2+kx+3=0的一个根为3,则k的值为( )
A.-4 B.4
C.-2 D.2
3.用配方法解方程x2+4x-5=0时,原方程应变形为( )
A.(x-2)2=1 B.(x-4)2=11
C.(x+2)2=9 D.(x+4)2=21
4.关于x的一元二次方程-kx2-6x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k>-3 B.k<3
C.k<3且k≠0 D.k>-3且k≠0
5.若对于任意实数a,b,c,d,定义=ad-bc,按照定义,若=0,则x的值为( )
A. B.-
C.3 D.±
6.某种商品经过两次涨价,每件零售价由200元涨至242元,求平均每次涨价的百分率.设平均每次涨价的百分率为x,则可列方程为( )
A.200(1+x)2=242 B.242(1-x)2=200
C.242(1-2x)=200 D.200(1+2x)=242
7.在△ABC中,AB=AC,BC=8,AB的长是方程x2-9x+20=0的一个根,则△ABC的周长为( )
A.16 B.16或18
C.17 D.18
8.已知x1,x2是一元二次方程x2-x-2=0的两个根,则+的值是( )
A.1 B.
C.-1 D.-
9.若直角三角形的两边长分别是方程x2-7x+12=0的两根,则该直角三角形的面积是( )
A.6 B.12
C.12或 D.6或
10.若m,n是方程x2-x-2 022=0的两个根,则代数式(m2-2m-2 022)(-n2+2n+2 022)的值为( )
A.2 023 B.2 022
C.2 021 D.2 020
二、填空题(每小题4分,共28分)
11.若关于x的方程xm+1-3=0是一元二次方程,则m=________.
12.若关于x的方程x2=a-1有实数根,则a的取值范围为________.
13.方程(x+3)2=x+3的根是____________.
14.若关于x的一元二次方程(k-1)x2+2kx+k+3=0有实数根,则k的取值范围是____________.
15.菱形的一条对角线长为8,其边长是方程x2-8x+15=0的一个根,则该菱形的面积为________.
16.若正数a是一元二次方程x2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,则a的值是________.
17.如图,在一块长为22 m,宽为14 m的矩形空地内修建三条宽度相等的小路(阴影部分),其余部分种植花草.若花草的种植面积为240 m2,则小路的宽为________m.
INCLUDEPICTURE"二改+1.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\二改+1.tif" \* MERGEFORMATINET
三、解答题(一)(每小题6分,共18分)
18.解方程:
(1)2x2-5x-3=0;
(2)x2-2x=2x-1;
(3)x2+3x+2=0.
19.用配方法求-3x2-6x+1的最大值.
20.已知关于x的一元二次方程x2-2 x+m=0有两个不相等的实数根,求实数m的最大整数值.
四、解答题(二)(每小题8分,共24分)
21.有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25,-16,第一次按键后,A,B两区分别显示25+a2,-16-3a.
(1)从初始状态按2次后,分别求A,B两区显示的结果;
(2)从初始状态按4次后,得A,B两区显示的代数式的和为1,求a的值.
22.关于x的一元二次方程x2-(k-3)x-2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程的两根分别为x1,x2,且x1+x2+x1x2=2,求k的值.
23.为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子产品的固定成本为100元,这种电子产品降价后的销售单价为多少元时,公司每天可获利32 000元?
五、解答题(三)(每小题10分,共20分)
24.如图,有一农户要建一个矩形鸡舍,鸡舍的一边利用长为a米的墙,另外三边用25米长的篱笆围成,为方便进出,在垂直于墙的一边CD上留一个1米宽的门.
(1)若a=12,当矩形鸡舍的边长分别为多少时,鸡舍的面积为80平方米?
(2)当a的值在什么范围时,(1)中的解有两个?一个?无解?
(3)若墙的长度足够长,鸡舍的面积能否为90平方米?
INCLUDEPICTURE"初排+13.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+13.tif" \* MERGEFORMATINET
25.请阅读下列材料.
问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程的根的2倍.
解:设所求方程的根为y,则y=2x,所以x=.
把x=代入已知方程,得+-1=0.
化简,得y2+2y-4=0.
故所求方程为y2+2y-4=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程的根的相反数;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程的根的倒数.
答案
一、1.C 2.A 3.C 4.D 5.D 6.A 7.D
8.D 9.D 10.B
二、11.1 12.a≥1 13.x1=-3,x2=-2
14.k≤且k≠1 15.24 16.5 17.2
三、18.解:(1)∵a=2,b=-5,c=-3,
∴b2-4ac=(-5)2-4×2×(-3)=49>0,
∴x==,∴x1=-,x2=3.
(2)移项,得x2-4x=-1.
配方,得x2-4x+4=-1+4,
即(x-2)2=3.
两边开平方,得x-2=±,
即x-2=或x-2=-.
∴x1=2+,x2=2-.
(3)原方程可变形为(x+1)(x+2)=0,
∴x+1=0或x+2=0.∴x1=-1,x2=-2.
19.解:-3x2-6x+1
=-3(x2+2x)+1
=-3(x2+2x+1-1)+1
=-3(x+1)2+4,
∵-3(x+1)2≤0,∴-3(x+1)2+4≤4,
∴-3x2-6x+1的最大值为4.
20.解:∵一元二次方程x2-2 x+m=0有两个不相等的实数根,∴Δ=8-4m>0,解得m<2.
∴实数m的最大整数值为1.
四、21.解:(1)25+a2+a2=25+2a2,
-16-3a-3a=-16-6a.
答:A区显示的结果为(25+2a2),B区显示的结果为(-16-6a).
(2)依题意,得25+4a2+(-16-12a)=1,
化简,得a2-3a+2=0,解得a1=2,a2=1.
答:a的值为2或1.
22.(1)证明:∵b2-4ac=[-(k-3)]2-4×1×(-2k+2)=k2+2k+1=(k+1)2≥0,
∴方程总有两个实数根.
(2)解:由根与系数的关系,得x1+x2=k-3,x1x2=-2k+2,
∴x1+x2+x1x2=(k-3)+(-2k+2)=2,解得k=-3.
23.解:设降价后的销售单价为x元,则降价后每天可售出[300+5(200-x)]个,
依题意,得(x-100)[300+5(200-x)]=32 000,
整理,得x2-360x+32 400=0,
解得x1=x2=180.
180<200,符合题意.
答:这种电子产品降价后的销售单价为180元时,公司每天可获利32 000元.
五、24.解:(1)设矩形鸡舍垂直于墙的一边长为x米,则平行于墙的一边长为(26-2x)米.
依题意,得x(26-2x)=80,
解得x1=5,x2=8.
当x=5时,26-2x=16>12(舍去),
当x=8时,26-2x=10<12.
答:当矩形鸡舍的长为10米,宽为8米时,鸡舍的面积为80平方米.
(2)由(1)知,平行于墙的一边长为10米或16米,
∴当a≥16时,(1)中的解有两个,
当10≤a<16时,(1)中的解有一个,
当0<a<10时,(1)无解.
(3)由题意,得x(26-2x)=90,
整理,得x2-13x+45=0,
则Δ=b2-4ac=169-180=-11<0,
故鸡舍的面积不能为90平方米.
25.解:(1)设所求方程的根为z,
则z=-x,所以x=-z.
把x=-z代入已知方程,得z2-z-2=0,
故所求方程为z2-z-2=0.
(2)设所求方程的根为t,
则t=(x≠0),所以x=(t≠0).
把x=代入方程ax2+bx+c=0,
得a+b·+c=0.
去分母,得a+bt+ct2=0.
若c=0,则有ax2+bx=0,所以方程ax2+bx+c=0有一个根为0,不符合题意,所以c≠0.
故所求方程为ct2+bt+a=0(c≠0).
PAGE
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
