北师大版九年级数学上册 第6章反比例函数评估卷(word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册 第6章反比例函数评估卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 252.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 12:50:32 | ||
图片预览




文档简介
北师大版九年级数学上册 第6章 学情评估卷
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、选择题(每小题3分,共30分)
1.下列函数表达式中属于反比例函数的是( )
A.y=3x B.y=-
C.y=x2+3 D.x+y=52
2.若反比例函数y=(k≠0)的图象经过点(2,4),则k的值是( )
A.2 B.-2 C.8 D.-8
3.已知在平面直角坐标系中,反比例函数y=的图象位于第二、四象限,则m的取值范围是( )
A.m<3 B.m>3
C.m>-3 D.m<-3
4.在平面直角坐标系中,点A(-1,2),B(2,3),C(-6,m)分别在三个不同的象限,若反比例函数y=(k≠0)的图象经过其中两点,则k的值为( )
A.-2 B.6
C.-2或6 D.-6
5.已知点(-1,y1),(-3,y2),(3,y3)在反比例函数y=-的图象上,则( )
A.y1C.y36.已知函数y=(m<0),以下结论中正确的有( )
①图象位于第一、三象限;
②若点A(-1,a),点B(1,b)在图象上,则a<b;
③对于不同的m值,反比例函数的图象可能会相交;
④若点P(x,y)在图象上,则点P1(-y,-x)也在图象上.
A.4个 B.3个
C.2个 D.1个
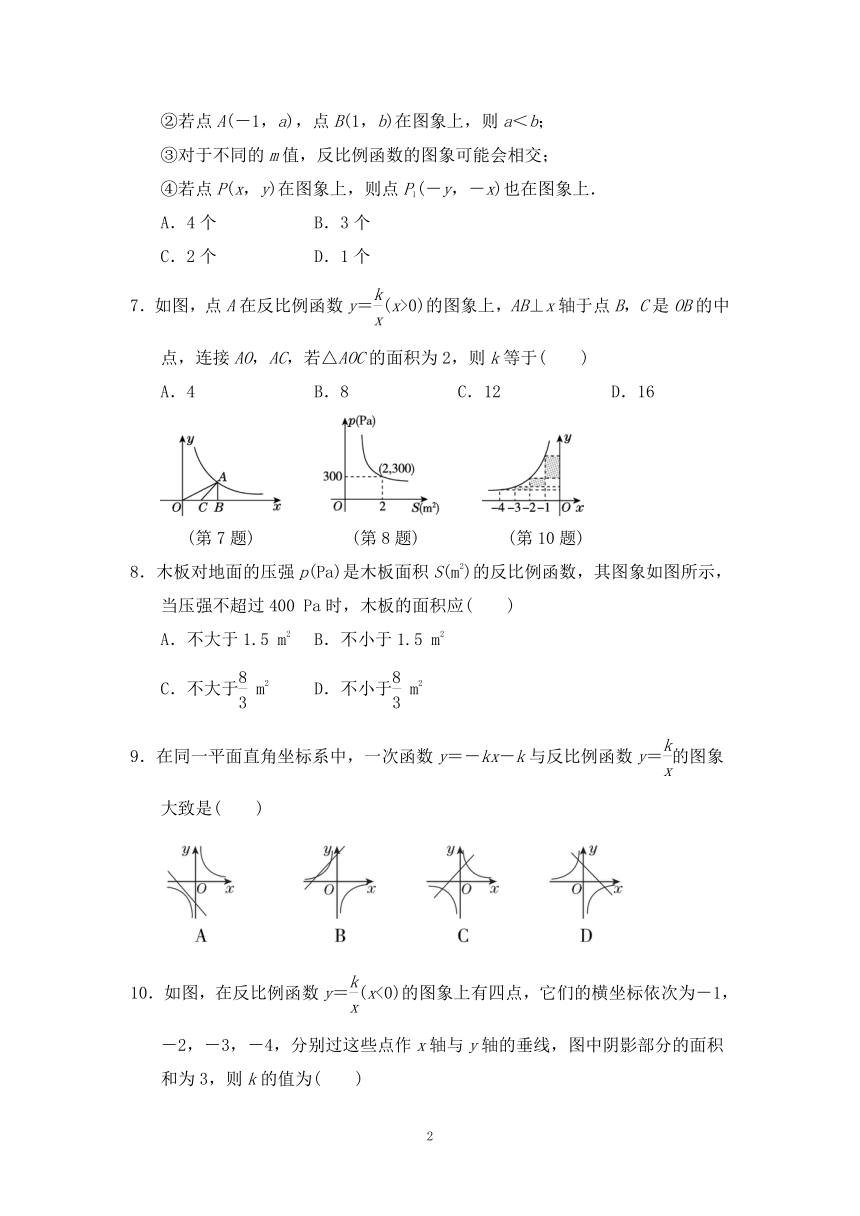
7.如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为2,则k等于( )
A.4 B.8 C.12 D.16
INCLUDEPICTURE"初排+70.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+70.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+71.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+71.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+76.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+76.tif" \* MERGEFORMATINET
(第7题) (第8题) (第10题)
8.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( )
A.不大于1.5 m2 B.不小于1.5 m2
C.不大于 m2 D.不小于 m2
9.在同一平面直角坐标系中,一次函数y=-kx-k与反比例函数y=的图象大致是( )
10.如图,在反比例函数y=(x<0)的图象上有四点,它们的横坐标依次为-1,-2,-3,-4,分别过这些点作x轴与y轴的垂线,图中阴影部分的面积和为3,则k的值为( )
A.-2 B.-3 C.-4 D.-6
二、填空题(每小题4分,共28分)
11.若y=(m是常数)是反比例函数,则m=________.
12.已知反比例函数y=的图象经过点(-2,4),则k的值为________.
13.在平面直角坐标系xOy中,直线y=2x与反比例函数y=(k≠0)的图象交于A,B两点.若点A,B的纵坐标分别是y1,y2,则y1+y2的值是________.
14.如图,点A在函数y=的图象上,过点A分别向x轴、y轴作垂线,垂足分别为点N、M,则四边形AMON的面积为________.
INCLUDEPICTURE"初排+77.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+77.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+78.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+78.tif" \* MERGEFORMATINET
(第14题) (第15题)
15.如图,点A是反比例函数y=(x<0)的图象上一点,AC⊥x轴于点C且与反比例函数y=(x<0)的图象交于点B,AB=3BC,连接OA,OB,若△OAB的面积为6,则k1+k2=________.
16.如图,在平面直角坐标系中,点A在函数y=-(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO,∠AOB=90°,则k的值为________.
INCLUDEPICTURE"初排+79.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+79.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+80.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+80.tif" \* MERGEFORMATINET
(第16题) (第17题)
17.如图,菱形OABC的两个顶点A,C在反比例函数y=(k≠0)的第一象限内的图象上,已知菱形OABC的面积为6,点B的坐标为(3 ,3 ),则k的值为________.
三、解答题(一)(每小题6分,共18分)
18.已知反比例函数y=(k≠0)的图象经过直线y=3x上的点P(,m),求m和k的值.
19.已知反比例函数y=的图象经过点(-3,2).
(1)求该反比例函数的表达式;
(2)在平面直角坐标系中画出该反比例函数的图象;
(3)若-3<x<-2,直接写出y的取值范围.
20.如图,等腰直角三角形POA的直角顶点P在反比例函数y=(x>0)的图象上,点A在x轴的正半轴上,求点A的坐标.
INCLUDEPICTURE"初排+81.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+81.tif" \* MERGEFORMATINET
四、解答题(二)(每小题8分,共24分)
21.一辆汽车准备从甲地开往乙地.若平均速度为80 km/h,则需要5 h到达.
(1)写出汽车从甲地到乙地所用时间t(h)与平均速度v(km/h)之间的关系式;
(2)如果准备用8 h到达,那么平均速度是多少?
(3)已知汽车的最大平均速度是100 km/h,那么汽车最少用多长时间可以到达?
22.已知y=y1+y2,若y1与x2成正比例关系,y2与x成反比例关系,且当x=-1时,y=3,当x=1时,y=-5,求y与x的函数表达式.
23.如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=(k≠0)的图象上.
(1)求点P′的坐标;
(2)求反比例函数的表达式,并直接写出当y2<2时自变量x的取值范围.
INCLUDEPICTURE"CC162.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\CC162.tif" \* MERGEFORMATINET
五、解答题(三)(每小题10分,共20分)
24.如图,直线y=x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根.
(1)求点B的坐标;
(2)双曲线y=(k≠0,x>0)与直线AB交于点C,且AC=5 ,求k的值.
INCLUDEPICTURE"CC163.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\CC163.tif" \* MERGEFORMATINET
25.如图,已知直线y=x+1与双曲线y=交于A,B两点,且点A的坐标为(a,2).
(1)求双曲线的表达式;
(2)将直线y=x+1向下平移一个单位长度得直线l,P是y轴上的一个动点,Q是l上的一个动点,求AP+PQ的最小值;
(3)若M为y轴上的一个动点,N为平面内一个动点,当以A,B,M,N为顶点的四边形是矩形时,直接写出点N的坐标.
INCLUDEPICTURE"初排+84.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+84.tif" \* MERGEFORMATINET
答案
一、1.B 2.C 3.B 4.B 5.D 6.D 7.B
8.B 9.A 10.C
二、11.2 12.-7 13.0 14.6 15.-20 16.1 17.4
三、18.解:把x=,y=m代入y=3x,得m=3 .
把x=,y=3 代入y=(k≠0),得k=9.
19.解:(1)∵反比例函数y=的图象经过点(-3,2),
∴2=,解得k=-6,
∴该反比例函数的表达式为y=-.
(2)该反比例函数的图象如图所示:
INCLUDEPICTURE"答案+29.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\答案+29.tif" \* MERGEFORMATINET
(3)2<y<3.
20.解:如图,过点P作x轴的垂线,点D为垂足.
∵△POA是等腰直角三角形,∴PD=OD=DA.
∵点P在反比例函数y=(x>0)的图象上,
∴OD·PD=4,∴OD=2,∴OA=4,
∴点A的坐标为(4,0).
INCLUDEPICTURE"答案+30.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\答案+30.tif" \* MERGEFORMATINET
四、21.解:(1)由题意得甲地到乙地的距离为80×5=400 km,∴vt=400,
∴汽车从甲地到乙地所用时间t(h)与平均速度 v(km/h)之间的关系式为t=.
(2)当t=8时,v==50,∴平均速度是50 km/h.
(3)当v=100时,t==4,∴汽车最少用4 h可以到达.
22.解:设y1=k1x2,y2=, 则y=k1x2+ .
依题意得
解得
∴y与x的函数表达式为y=-x2-.
23.解:(1)∵直线y1=-2x经过点P(-2,a),
∴a=-2×(-2)=4.
∴点P的坐标是(-2,4).
∴点P关于y轴的对称点P′的坐标是(2,4).
(2)∵点P′(2,4)在反比例函数y2=(k≠0)的图象上,∴4=,解得k=8.
∴反比例函数的表达式是y2=.
当y2<2时,自变量x的取值范围是x>4或x<0.
五、24.解:(1)解方程x2-7x-8=0,得x=8或x=-1.
∵线段OA的长是方程x2-7x-8=0的一个根,
∴OA=8.∴A(-8,0).
将点A(-8,0)的坐标代入y=x+b,得-4+b=0,解得b=4,∴B(0,4).
(2)在Rt△AOB中,OA=8,OB=4,
∴AB===4 .
过点C作CH⊥x轴于点H.
则∠AHC=∠AOB=90°.
又∵∠CAH=∠BAO,∴△AHC∽△AOB.
∴==.
∵AC=5 ,∴==.
解得CH=5,AH=10,
∴OH=AH-AO=10-8=2.∴C(2,5).
∵双曲线y=(k≠0,x>0)经过点C,
∴k=2×5=10.
25.解:(1)由题意得a=1, ∴A(1,2),
易得k=2, ∴双曲线的表达式为y=.
(2)如图,作A关于y轴的对称点A′,AA′交y轴于K,过A′作A′Q⊥l于Q,交y轴于P,此时AP+PQ取得最小值,AP+PQ=A′P+PQ=A′Q.
INCLUDEPICTURE"答案+31.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\答案+31.tif" \* MERGEFORMATINET
易得AK=A′K=1,OK=2,∠AKP=∠A′KP=90°.
∵将直线y=x+1向下平移一个单位长度得直线l,
∴直线l的表达式为y=x,∴∠POQ=45°,
∴∠OPQ=45°,∴∠A′PK=∠KA′P=45°,
∴A′K=PK=1,∴A′P=,OP=OK-PK=1.
易得PQ=OQ,PQ2+OQ2=OP2,
∴PQ=, ∴A′Q=A′P+PQ=+=.
∴AP+PQ的最小值为.
(3)当以A,B,M,N为顶点的四边形是矩形时,点N的坐标为(-3,0)或(3,0)或(-1,-)或.
PAGE
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、选择题(每小题3分,共30分)
1.下列函数表达式中属于反比例函数的是( )
A.y=3x B.y=-
C.y=x2+3 D.x+y=52
2.若反比例函数y=(k≠0)的图象经过点(2,4),则k的值是( )
A.2 B.-2 C.8 D.-8
3.已知在平面直角坐标系中,反比例函数y=的图象位于第二、四象限,则m的取值范围是( )
A.m<3 B.m>3
C.m>-3 D.m<-3
4.在平面直角坐标系中,点A(-1,2),B(2,3),C(-6,m)分别在三个不同的象限,若反比例函数y=(k≠0)的图象经过其中两点,则k的值为( )
A.-2 B.6
C.-2或6 D.-6
5.已知点(-1,y1),(-3,y2),(3,y3)在反比例函数y=-的图象上,则( )
A.y1
①图象位于第一、三象限;
②若点A(-1,a),点B(1,b)在图象上,则a<b;
③对于不同的m值,反比例函数的图象可能会相交;
④若点P(x,y)在图象上,则点P1(-y,-x)也在图象上.
A.4个 B.3个
C.2个 D.1个
7.如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为2,则k等于( )
A.4 B.8 C.12 D.16
INCLUDEPICTURE"初排+70.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+70.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+71.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+71.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+76.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+76.tif" \* MERGEFORMATINET
(第7题) (第8题) (第10题)
8.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( )
A.不大于1.5 m2 B.不小于1.5 m2
C.不大于 m2 D.不小于 m2
9.在同一平面直角坐标系中,一次函数y=-kx-k与反比例函数y=的图象大致是( )
10.如图,在反比例函数y=(x<0)的图象上有四点,它们的横坐标依次为-1,-2,-3,-4,分别过这些点作x轴与y轴的垂线,图中阴影部分的面积和为3,则k的值为( )
A.-2 B.-3 C.-4 D.-6
二、填空题(每小题4分,共28分)
11.若y=(m是常数)是反比例函数,则m=________.
12.已知反比例函数y=的图象经过点(-2,4),则k的值为________.
13.在平面直角坐标系xOy中,直线y=2x与反比例函数y=(k≠0)的图象交于A,B两点.若点A,B的纵坐标分别是y1,y2,则y1+y2的值是________.
14.如图,点A在函数y=的图象上,过点A分别向x轴、y轴作垂线,垂足分别为点N、M,则四边形AMON的面积为________.
INCLUDEPICTURE"初排+77.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+77.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+78.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+78.tif" \* MERGEFORMATINET
(第14题) (第15题)
15.如图,点A是反比例函数y=(x<0)的图象上一点,AC⊥x轴于点C且与反比例函数y=(x<0)的图象交于点B,AB=3BC,连接OA,OB,若△OAB的面积为6,则k1+k2=________.
16.如图,在平面直角坐标系中,点A在函数y=-(x<0)的图象上,点B在函数y=(x>0)的图象上,若AO=2BO,∠AOB=90°,则k的值为________.
INCLUDEPICTURE"初排+79.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+79.tif" \* MERGEFORMATINET INCLUDEPICTURE"初排+80.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+80.tif" \* MERGEFORMATINET
(第16题) (第17题)
17.如图,菱形OABC的两个顶点A,C在反比例函数y=(k≠0)的第一象限内的图象上,已知菱形OABC的面积为6,点B的坐标为(3 ,3 ),则k的值为________.
三、解答题(一)(每小题6分,共18分)
18.已知反比例函数y=(k≠0)的图象经过直线y=3x上的点P(,m),求m和k的值.
19.已知反比例函数y=的图象经过点(-3,2).
(1)求该反比例函数的表达式;
(2)在平面直角坐标系中画出该反比例函数的图象;
(3)若-3<x<-2,直接写出y的取值范围.
20.如图,等腰直角三角形POA的直角顶点P在反比例函数y=(x>0)的图象上,点A在x轴的正半轴上,求点A的坐标.
INCLUDEPICTURE"初排+81.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+81.tif" \* MERGEFORMATINET
四、解答题(二)(每小题8分,共24分)
21.一辆汽车准备从甲地开往乙地.若平均速度为80 km/h,则需要5 h到达.
(1)写出汽车从甲地到乙地所用时间t(h)与平均速度v(km/h)之间的关系式;
(2)如果准备用8 h到达,那么平均速度是多少?
(3)已知汽车的最大平均速度是100 km/h,那么汽车最少用多长时间可以到达?
22.已知y=y1+y2,若y1与x2成正比例关系,y2与x成反比例关系,且当x=-1时,y=3,当x=1时,y=-5,求y与x的函数表达式.
23.如图,已知直线y1=-2x经过点P(-2,a),点P关于y轴的对称点P′在反比例函数y2=(k≠0)的图象上.
(1)求点P′的坐标;
(2)求反比例函数的表达式,并直接写出当y2<2时自变量x的取值范围.
INCLUDEPICTURE"CC162.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\CC162.tif" \* MERGEFORMATINET
五、解答题(三)(每小题10分,共20分)
24.如图,直线y=x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根.
(1)求点B的坐标;
(2)双曲线y=(k≠0,x>0)与直线AB交于点C,且AC=5 ,求k的值.
INCLUDEPICTURE"CC163.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\CC163.tif" \* MERGEFORMATINET
25.如图,已知直线y=x+1与双曲线y=交于A,B两点,且点A的坐标为(a,2).
(1)求双曲线的表达式;
(2)将直线y=x+1向下平移一个单位长度得直线l,P是y轴上的一个动点,Q是l上的一个动点,求AP+PQ的最小值;
(3)若M为y轴上的一个动点,N为平面内一个动点,当以A,B,M,N为顶点的四边形是矩形时,直接写出点N的坐标.
INCLUDEPICTURE"初排+84.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\初排+84.tif" \* MERGEFORMATINET
答案
一、1.B 2.C 3.B 4.B 5.D 6.D 7.B
8.B 9.A 10.C
二、11.2 12.-7 13.0 14.6 15.-20 16.1 17.4
三、18.解:把x=,y=m代入y=3x,得m=3 .
把x=,y=3 代入y=(k≠0),得k=9.
19.解:(1)∵反比例函数y=的图象经过点(-3,2),
∴2=,解得k=-6,
∴该反比例函数的表达式为y=-.
(2)该反比例函数的图象如图所示:
INCLUDEPICTURE"答案+29.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\答案+29.tif" \* MERGEFORMATINET
(3)2<y<3.
20.解:如图,过点P作x轴的垂线,点D为垂足.
∵△POA是等腰直角三角形,∴PD=OD=DA.
∵点P在反比例函数y=(x>0)的图象上,
∴OD·PD=4,∴OD=2,∴OA=4,
∴点A的坐标为(4,0).
INCLUDEPICTURE"答案+30.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\答案+30.tif" \* MERGEFORMATINET
四、21.解:(1)由题意得甲地到乙地的距离为80×5=400 km,∴vt=400,
∴汽车从甲地到乙地所用时间t(h)与平均速度 v(km/h)之间的关系式为t=.
(2)当t=8时,v==50,∴平均速度是50 km/h.
(3)当v=100时,t==4,∴汽车最少用4 h可以到达.
22.解:设y1=k1x2,y2=, 则y=k1x2+ .
依题意得
解得
∴y与x的函数表达式为y=-x2-.
23.解:(1)∵直线y1=-2x经过点P(-2,a),
∴a=-2×(-2)=4.
∴点P的坐标是(-2,4).
∴点P关于y轴的对称点P′的坐标是(2,4).
(2)∵点P′(2,4)在反比例函数y2=(k≠0)的图象上,∴4=,解得k=8.
∴反比例函数的表达式是y2=.
当y2<2时,自变量x的取值范围是x>4或x<0.
五、24.解:(1)解方程x2-7x-8=0,得x=8或x=-1.
∵线段OA的长是方程x2-7x-8=0的一个根,
∴OA=8.∴A(-8,0).
将点A(-8,0)的坐标代入y=x+b,得-4+b=0,解得b=4,∴B(0,4).
(2)在Rt△AOB中,OA=8,OB=4,
∴AB===4 .
过点C作CH⊥x轴于点H.
则∠AHC=∠AOB=90°.
又∵∠CAH=∠BAO,∴△AHC∽△AOB.
∴==.
∵AC=5 ,∴==.
解得CH=5,AH=10,
∴OH=AH-AO=10-8=2.∴C(2,5).
∵双曲线y=(k≠0,x>0)经过点C,
∴k=2×5=10.
25.解:(1)由题意得a=1, ∴A(1,2),
易得k=2, ∴双曲线的表达式为y=.
(2)如图,作A关于y轴的对称点A′,AA′交y轴于K,过A′作A′Q⊥l于Q,交y轴于P,此时AP+PQ取得最小值,AP+PQ=A′P+PQ=A′Q.
INCLUDEPICTURE"答案+31.tif" INCLUDEPICTURE "F:\\22秋\\9年级\\9BS广东\\答案+31.tif" \* MERGEFORMATINET
易得AK=A′K=1,OK=2,∠AKP=∠A′KP=90°.
∵将直线y=x+1向下平移一个单位长度得直线l,
∴直线l的表达式为y=x,∴∠POQ=45°,
∴∠OPQ=45°,∴∠A′PK=∠KA′P=45°,
∴A′K=PK=1,∴A′P=,OP=OK-PK=1.
易得PQ=OQ,PQ2+OQ2=OP2,
∴PQ=, ∴A′Q=A′P+PQ=+=.
∴AP+PQ的最小值为.
(3)当以A,B,M,N为顶点的四边形是矩形时,点N的坐标为(-3,0)或(3,0)或(-1,-)或.
PAGE
同课章节目录
