9.4.2 利用边角关系判定三角形相似同步练习(含答案)
文档属性
| 名称 | 9.4.2 利用边角关系判定三角形相似同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用边角关系判定三角形相似
知识梳理
定理:两边成比例且______相等的两个三角形相似.
巩固提高
1.在△ABC和△DEF中,△∠B=△∠E=100°,下列条件不能得到两个三角形相似的是( )
A.∠A=∠D C.∠C=∠D D.∠C=40°,∠D=30°
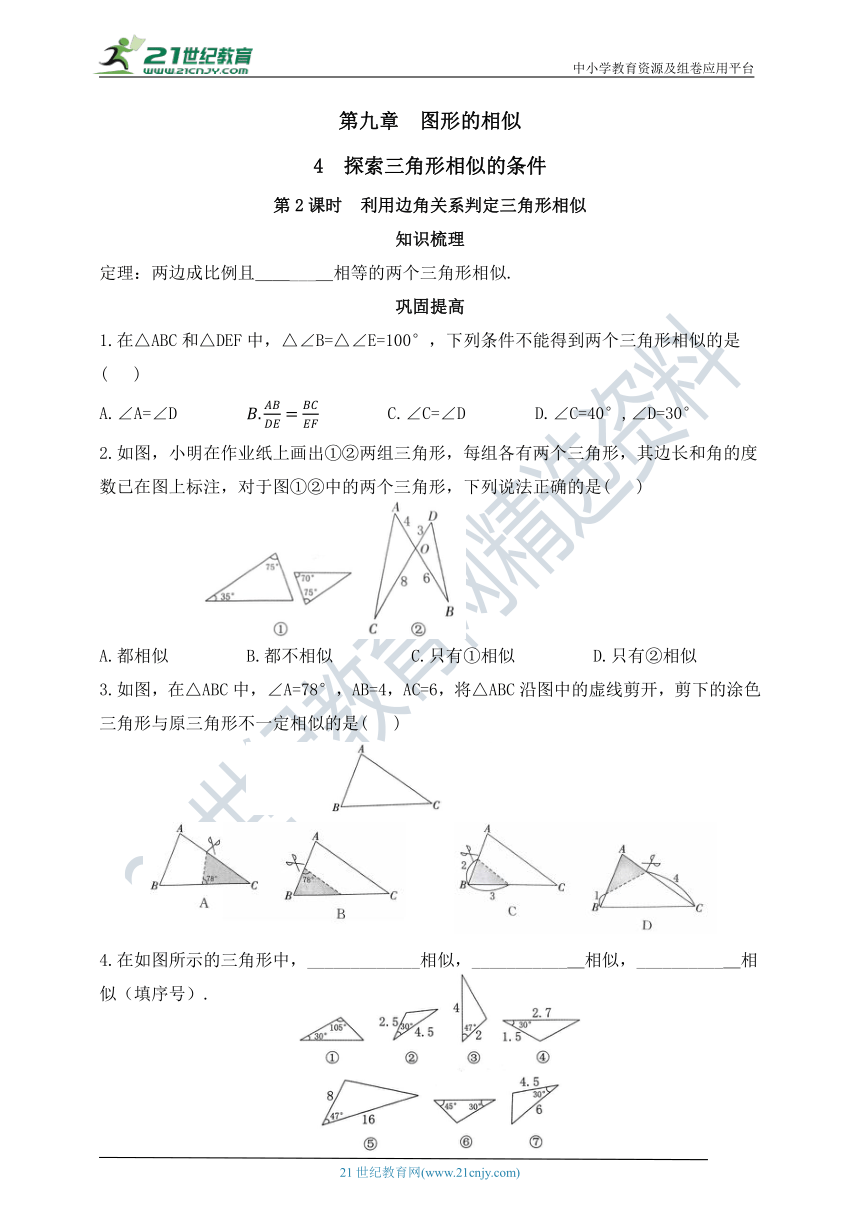
2.如图,小明在作业纸上画出①②两组三角形,每组各有两个三角形,其边长和角的度数已在图上标注,对于图①②中的两个三角形,下列说法正确的是( )
A.都相似 B.都不相似 C.只有①相似 D.只有②相似
3.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图中的虚线剪开,剪下的涂色三角形与原三角形不一定相似的是( )
4.在如图所示的三角形中,_____________相似,____________相似,___________相似(填序号).
5.如图,∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.找出图中相似的三角形,并证明.
巩固提高
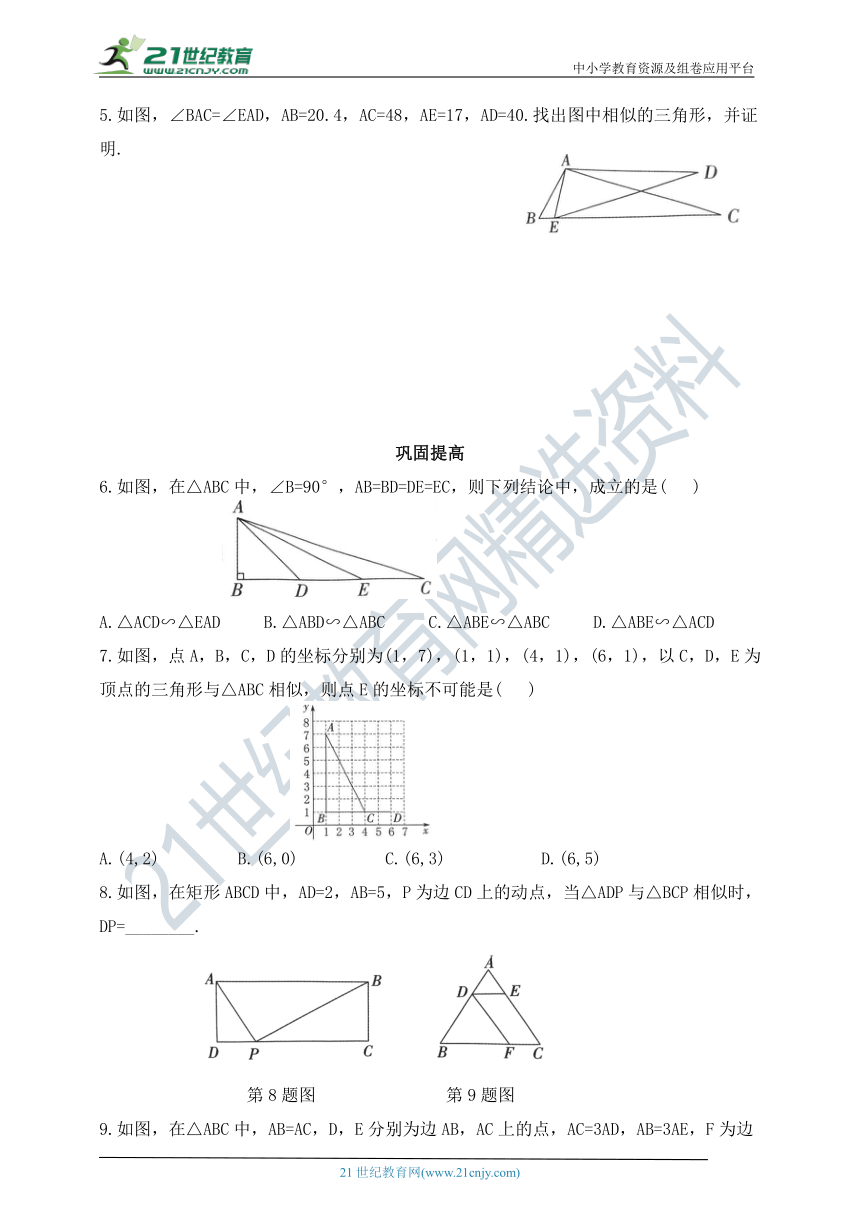
6.如图,在△ABC中,∠B=90°,AB=BD=DE=EC,则下列结论中,成立的是( )
A.△ACD∽△EAD B.△ABD∽△ABC C.△ABE∽△ABC D.△ABE∽△ACD
7.如图,点A,B,C,D的坐标分别为(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,2) B.(6,0) C.(6,3) D.(6,5)
8.如图,在矩形ABCD中,AD=2,AB=5,P为边CD上的动点,当△ADP与△BCP相似时,DP=________.
第8题图 第9题图
9.如图,在△ABC中,AB=AC,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,F为边BC上的一点,添加一个条件:_______________,可以使得△FDB与△ADE相似(只需写出一个).
10.如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF:DC=1∶4,连接EF并延长交BC的延长线于点G,连接BE.
(1)求证:△ABE∽△DEF;
(2)若正方形ABCD的边长为10,求BG的长.
11.如图,在△ABC中,AB=8,AC=16,点P从点B开始沿边BA向点A以2个单位长度/秒的速度移动,点Q从点A开始沿边AC向点C以4个单位长度/秒的速度移动.如果点P,Q分别从点B,A同时出发,那么经过多少秒时,以A,P,Q为顶点的三角形与△ABC相似
12.如图,在△ABC中,AB=AC,点E在边BC上移动(不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点处时,求证:FE平分∠DFC.
参考答案
[知识梳理]
夹角
[基础练习]
1.D 2.A 3.C 4. ①⑥ ②④ ③⑤
5.△ABC∽△AED ∵AB=20.4,AC=48,AE=17,AD=40,∴ 又∵∠BAC=∠EAD,∴△ABC∽△AED.
[巩固提高]
6.A 7.C 8.1或4或2.5 9.答案不唯一,如DF∥AC
10.(1)∵四边形ABCD是正方形,∴∠A=∠D=90°,AB=AD=CD.∵AE=ED,DF:DC=1:4,∴AE=
又∵∠A=∠D,
∴△ABE∽△DEF.
(2)∵BC=AD=CD=10,∴AE=∵AD∥B=∠GCF.
又∵∠DFE=∠CFG,∴△∽△ ,即 .∴CG=15. .
11.设经过t秒时,以A,P,Q为顶点的三角形与△ABC相似,则BP=2t,AP=8-2t,AQ=4t.
∵∠PAQ=∠BAC,∴当 时,△APQ∽△ABC,即 解得t=2;当 时,△APQ∽△ACB,即 解得t=0.8.∴经过2秒或0.8秒时,以A,P,Q为顶点的三角形与△ABC相似.
12.(1)∵AB=AC,∴∠B=∠C.∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,又∵∠DEF=∠B,∴∠BDE=∠CEF.∴△BDE∽△CEF.
(2)∵△BDE∽△CEF,∴ ∵E是BC的中点,即 ∠C,∴△DEF∽△ECF.∴∠DFE=∠EFC.∴FE平分∠DFC .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用边角关系判定三角形相似
知识梳理
定理:两边成比例且______相等的两个三角形相似.
巩固提高
1.在△ABC和△DEF中,△∠B=△∠E=100°,下列条件不能得到两个三角形相似的是( )
A.∠A=∠D C.∠C=∠D D.∠C=40°,∠D=30°
2.如图,小明在作业纸上画出①②两组三角形,每组各有两个三角形,其边长和角的度数已在图上标注,对于图①②中的两个三角形,下列说法正确的是( )
A.都相似 B.都不相似 C.只有①相似 D.只有②相似
3.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图中的虚线剪开,剪下的涂色三角形与原三角形不一定相似的是( )
4.在如图所示的三角形中,_____________相似,____________相似,___________相似(填序号).
5.如图,∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.找出图中相似的三角形,并证明.
巩固提高
6.如图,在△ABC中,∠B=90°,AB=BD=DE=EC,则下列结论中,成立的是( )
A.△ACD∽△EAD B.△ABD∽△ABC C.△ABE∽△ABC D.△ABE∽△ACD
7.如图,点A,B,C,D的坐标分别为(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,2) B.(6,0) C.(6,3) D.(6,5)
8.如图,在矩形ABCD中,AD=2,AB=5,P为边CD上的动点,当△ADP与△BCP相似时,DP=________.
第8题图 第9题图
9.如图,在△ABC中,AB=AC,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,F为边BC上的一点,添加一个条件:_______________,可以使得△FDB与△ADE相似(只需写出一个).
10.如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF:DC=1∶4,连接EF并延长交BC的延长线于点G,连接BE.
(1)求证:△ABE∽△DEF;
(2)若正方形ABCD的边长为10,求BG的长.
11.如图,在△ABC中,AB=8,AC=16,点P从点B开始沿边BA向点A以2个单位长度/秒的速度移动,点Q从点A开始沿边AC向点C以4个单位长度/秒的速度移动.如果点P,Q分别从点B,A同时出发,那么经过多少秒时,以A,P,Q为顶点的三角形与△ABC相似
12.如图,在△ABC中,AB=AC,点E在边BC上移动(不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点处时,求证:FE平分∠DFC.
参考答案
[知识梳理]
夹角
[基础练习]
1.D 2.A 3.C 4. ①⑥ ②④ ③⑤
5.△ABC∽△AED ∵AB=20.4,AC=48,AE=17,AD=40,∴ 又∵∠BAC=∠EAD,∴△ABC∽△AED.
[巩固提高]
6.A 7.C 8.1或4或2.5 9.答案不唯一,如DF∥AC
10.(1)∵四边形ABCD是正方形,∴∠A=∠D=90°,AB=AD=CD.∵AE=ED,DF:DC=1:4,∴AE=
又∵∠A=∠D,
∴△ABE∽△DEF.
(2)∵BC=AD=CD=10,∴AE=∵AD∥B=∠GCF.
又∵∠DFE=∠CFG,∴△∽△ ,即 .∴CG=15. .
11.设经过t秒时,以A,P,Q为顶点的三角形与△ABC相似,则BP=2t,AP=8-2t,AQ=4t.
∵∠PAQ=∠BAC,∴当 时,△APQ∽△ABC,即 解得t=2;当 时,△APQ∽△ACB,即 解得t=0.8.∴经过2秒或0.8秒时,以A,P,Q为顶点的三角形与△ABC相似.
12.(1)∵AB=AC,∴∠B=∠C.∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,又∵∠DEF=∠B,∴∠BDE=∠CEF.∴△BDE∽△CEF.
(2)∵△BDE∽△CEF,∴ ∵E是BC的中点,即 ∠C,∴△DEF∽△ECF.∴∠DFE=∠EFC.∴FE平分∠DFC .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
