七年级数学上册目标测试卷七:第4章 几何图形初步(含答案)
文档属性
| 名称 | 七年级数学上册目标测试卷七:第4章 几何图形初步(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 348.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 14:12:45 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2021年秋季七年级数学目标测试卷(七)
(第4章 几何图形初步)
题 号 一 二 三 四 五 六 总分
得 分
一、选择题(本大题共6小题,每小题3分,共18分)
1.电筒发射出来的光线,给我们的感觉是( ).
A. 线段 B. 射线 C. 直线 D. 折线
2.甲看乙的方向为北偏东30°,那么乙看甲的方向是( ).
A. 南偏西30° B. 南偏东60° C.南偏西60° D.南偏东30°
3.如图,钟表8时30分时,时针与分针所成的角的度数为( ).
A. 30° B. 60° C.75° D. 90°
4.如图,下列说法不正确的是( ).
A.∠1与∠AOB是同一个角 B. ∠AOC也可用∠O来表示
C. 图中共有三个角:∠AOB, ∠AOC, ∠BOC D. ∠与∠BOC是同一个角
第3题图 第4题图 第5题图
5.将两块直角三角板的直角顶点重合,如图所示,若∠AOD=1280,则∠BOC的度数是( ).
A. 45° B.50° C. 60° D. 52°
6.如图的几何体,左视图是( ).
二、填空题(本大题共8小题,每小题3分,共24分)
7.如图,经过刨平的木板上的两个点,能弹出一条笔直的
墨线,此操作的依据是 .
8.45.3度= ° ′.
9.看图填空AM=AB-MN- .
10.如果一个角是64°,那么这个角的余角为 °.
11.已知CB=5,DB=7,D是AC的中点, 则AC=_________ .
12.已知线段AB=6cm,在直线AB上画线段AC=2cm,则BC的长是 cm.
13.观察下列各正方形图案,每条边上有个圆点,每个图案中圆点的总数是.
按此规律推断出与的关系式为是 .
14.如图,各图中的阴影部分绕着直线旋转360°,所形成的
立体图形分别是 .
三、(本大题共4小题,每小题6分,共24分)
15.A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
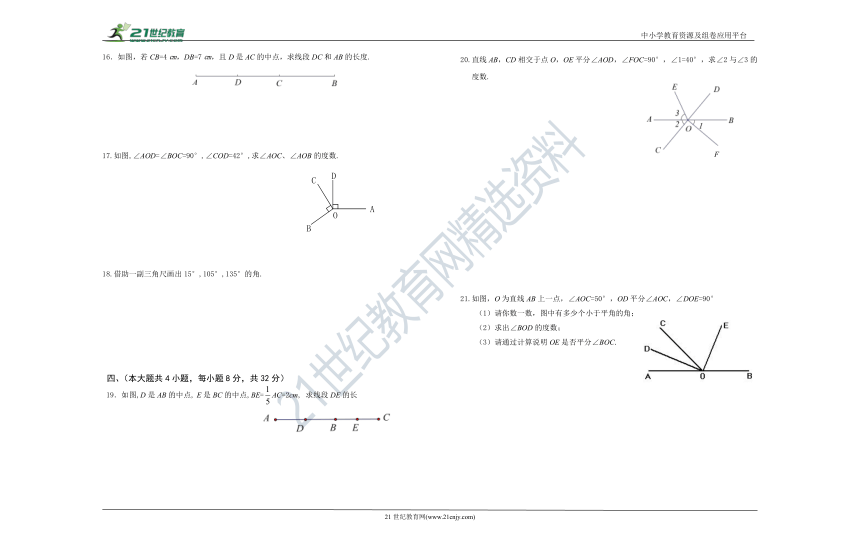
16.如图,若CB=4㎝,DB=7㎝,且D是AC的中点,求线段DC和AB的长度.
17.如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC、∠AOB的度数.
18.借助一副三角尺画出15°,105°,135°的角.
四、(本大题共4小题,每小题8分,共32分)
19.如图,D是AB的中点, E是BC的中点,BE=AC=2cm, 求线段DE的长
20.直线AB,CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
F
21.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
22.下面是小林解的一道题:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图形
∠AOC=∠BOA-∠BOC=70°-15°=55°
若你是老师,会判小林满分吗?若会,说明理由.若不会,请将小林的错误指出,并给出你认为正确的解法.
五、(本大题共10分)
23.如图看,李峰拿一张正方形的纸片(图①),将其沿虚线对折一次得图②,再沿图②中的虚线对折得图③,然后用剪刀沿图③中的虚线剪去一个角再打开,请你画出打开后的几何图形.
六、(本大题共12分)
24.下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形。
仔细观察图形可知:
图1中有1块黑色的瓷砖,可表示为1=;
图2中有3块黑色的瓷砖,可表示为1+2=;
图3中有6块黑色的瓷砖,可表示为1+2+3=;
实践与探索:
(1)请在图4中的虚线框内画出第4个图形
(2)第10个图形有 块黑色的瓷砖;第n个图形有 块黑色的瓷砖.
2021年秋季七年级数学目标测试卷(七)
(第4章 几何图形初步 参考答案)
一、选择题: 1. B 2.A 3. C 4.B 5.D 6. B
二、填空题: 7.两点确定一条直线 8. 45° 、 18′. 9.NB. 10. 26°.
11.4 . 12.4或8 . 13.4n -4. 14.圆柱、圆锥、球.
三、15.略 (理由:两点之间线段最短) 16.DC=3㎝,AB=10㎝.
17.∠AOC=132° ∠AOB=138° 18.略
四、 19.DE=5 20. ∠2=50°,∠3=65°.
21.(1)图中有9个小于平角的角;(2)155°
(3)因为 ∠BOE =180°-∠DOE-∠AOD=180°-90°-25°=65°,∠COE = 90°-25°=65 ,所以 ∠BOE =∠COE,即OE平分∠BOE.
22.解:小林不会得满分的.小林考虑的问题不全面,除了上述问题∠BOC在∠BOA内部以外,还有另一种情况∠BOC在∠BOA的外部.解法如下:根据题意可画出图形
∴∠AOC=∠BOA+∠BOC =70°+15°=85°
综合以上两种情况,∠AOC=55°或85°.
五、 23.略.
六、 24.解:(1)略,(2)55,n(n+1),(n为正整数)
1学校: 班级: 姓名: 座位号: 1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
,
,
,
A
B
l
A
O
B
C
③
②
①
①
1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
图1
图2
图3
图4
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2021年秋季七年级数学目标测试卷(七)
(第4章 几何图形初步)
题 号 一 二 三 四 五 六 总分
得 分
一、选择题(本大题共6小题,每小题3分,共18分)
1.电筒发射出来的光线,给我们的感觉是( ).
A. 线段 B. 射线 C. 直线 D. 折线
2.甲看乙的方向为北偏东30°,那么乙看甲的方向是( ).
A. 南偏西30° B. 南偏东60° C.南偏西60° D.南偏东30°
3.如图,钟表8时30分时,时针与分针所成的角的度数为( ).
A. 30° B. 60° C.75° D. 90°
4.如图,下列说法不正确的是( ).
A.∠1与∠AOB是同一个角 B. ∠AOC也可用∠O来表示
C. 图中共有三个角:∠AOB, ∠AOC, ∠BOC D. ∠与∠BOC是同一个角
第3题图 第4题图 第5题图
5.将两块直角三角板的直角顶点重合,如图所示,若∠AOD=1280,则∠BOC的度数是( ).
A. 45° B.50° C. 60° D. 52°
6.如图的几何体,左视图是( ).
二、填空题(本大题共8小题,每小题3分,共24分)
7.如图,经过刨平的木板上的两个点,能弹出一条笔直的
墨线,此操作的依据是 .
8.45.3度= ° ′.
9.看图填空AM=AB-MN- .
10.如果一个角是64°,那么这个角的余角为 °.
11.已知CB=5,DB=7,D是AC的中点, 则AC=_________ .
12.已知线段AB=6cm,在直线AB上画线段AC=2cm,则BC的长是 cm.
13.观察下列各正方形图案,每条边上有个圆点,每个图案中圆点的总数是.
按此规律推断出与的关系式为是 .
14.如图,各图中的阴影部分绕着直线旋转360°,所形成的
立体图形分别是 .
三、(本大题共4小题,每小题6分,共24分)
15.A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
16.如图,若CB=4㎝,DB=7㎝,且D是AC的中点,求线段DC和AB的长度.
17.如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC、∠AOB的度数.
18.借助一副三角尺画出15°,105°,135°的角.
四、(本大题共4小题,每小题8分,共32分)
19.如图,D是AB的中点, E是BC的中点,BE=AC=2cm, 求线段DE的长
20.直线AB,CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
F
21.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
22.下面是小林解的一道题:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图形
∠AOC=∠BOA-∠BOC=70°-15°=55°
若你是老师,会判小林满分吗?若会,说明理由.若不会,请将小林的错误指出,并给出你认为正确的解法.
五、(本大题共10分)
23.如图看,李峰拿一张正方形的纸片(图①),将其沿虚线对折一次得图②,再沿图②中的虚线对折得图③,然后用剪刀沿图③中的虚线剪去一个角再打开,请你画出打开后的几何图形.
六、(本大题共12分)
24.下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形。
仔细观察图形可知:
图1中有1块黑色的瓷砖,可表示为1=;
图2中有3块黑色的瓷砖,可表示为1+2=;
图3中有6块黑色的瓷砖,可表示为1+2+3=;
实践与探索:
(1)请在图4中的虚线框内画出第4个图形
(2)第10个图形有 块黑色的瓷砖;第n个图形有 块黑色的瓷砖.
2021年秋季七年级数学目标测试卷(七)
(第4章 几何图形初步 参考答案)
一、选择题: 1. B 2.A 3. C 4.B 5.D 6. B
二、填空题: 7.两点确定一条直线 8. 45° 、 18′. 9.NB. 10. 26°.
11.4 . 12.4或8 . 13.4n -4. 14.圆柱、圆锥、球.
三、15.略 (理由:两点之间线段最短) 16.DC=3㎝,AB=10㎝.
17.∠AOC=132° ∠AOB=138° 18.略
四、 19.DE=5 20. ∠2=50°,∠3=65°.
21.(1)图中有9个小于平角的角;(2)155°
(3)因为 ∠BOE =180°-∠DOE-∠AOD=180°-90°-25°=65°,∠COE = 90°-25°=65 ,所以 ∠BOE =∠COE,即OE平分∠BOE.
22.解:小林不会得满分的.小林考虑的问题不全面,除了上述问题∠BOC在∠BOA内部以外,还有另一种情况∠BOC在∠BOA的外部.解法如下:根据题意可画出图形
∴∠AOC=∠BOA+∠BOC =70°+15°=85°
综合以上两种情况,∠AOC=55°或85°.
五、 23.略.
六、 24.解:(1)略,(2)55,n(n+1),(n为正整数)
1学校: 班级: 姓名: 座位号: 1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
,
,
,
A
B
l
A
O
B
C
③
②
①
①
1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
图1
图2
图3
图4
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
