第13章 相交线、平行线填空题练习(上海地区专用)2021-2022学年下学期上海市各地沪教版七年级数学期中复习 (word版含解析)
文档属性
| 名称 | 第13章 相交线、平行线填空题练习(上海地区专用)2021-2022学年下学期上海市各地沪教版七年级数学期中复习 (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 614.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览


文档简介
第13章 相交线 平行线填空题
1.(2021·上海松江·七年级期中)如图,和∠A是同位角的有___.
2.(2021·上海市罗南中学七年级期中)如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是____.(填序号)
3.(2021·上海·七年级期中)如图,射线,相交于点,则的内错角是__.
4.(2021·上海浦东新·七年级期中)如图,∠E的同位角有___个.
5.(2021·上海市罗南中学七年级期中)在同一平面内,两条不相重合的直线位置关系有两种:_____和_____.
6.(2021·上海市浦东新区新场实验中学七年级期中)如图,平分,,,则________∥________
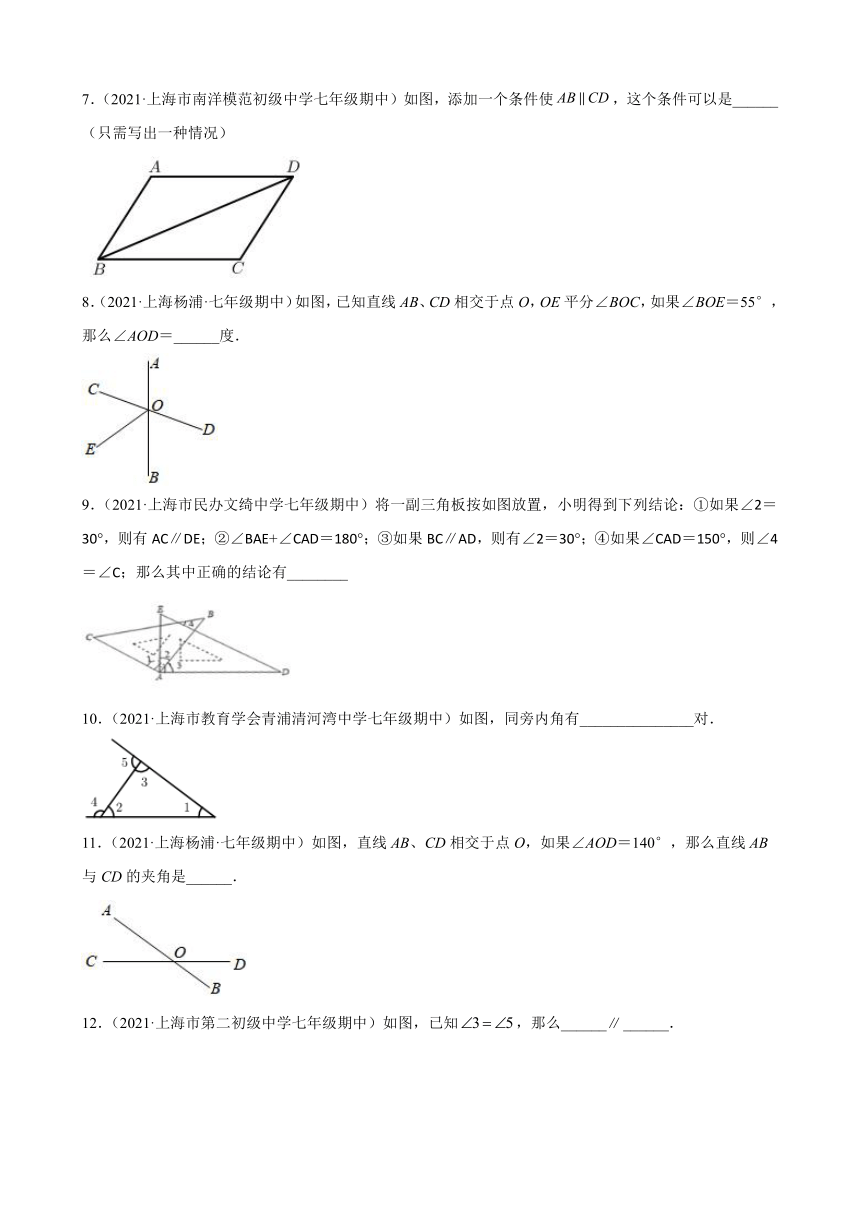
7.(2021·上海市南洋模范初级中学七年级期中)如图,添加一个条件使,这个条件可以是______(只需写出一种情况)
8.(2021·上海杨浦·七年级期中)如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=55°,那么∠AOD=______度.
9.(2021·上海市民办文绮中学七年级期中)将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有________
10.(2021·上海市教育学会青浦清河湾中学七年级期中)如图,同旁内角有_______________对.
11.(2021·上海杨浦·七年级期中)如图,直线AB、CD相交于点O,如果∠AOD=140°,那么直线AB与CD的夹角是______.
12.(2021·上海市第二初级中学七年级期中)如图,已知,那么____________.
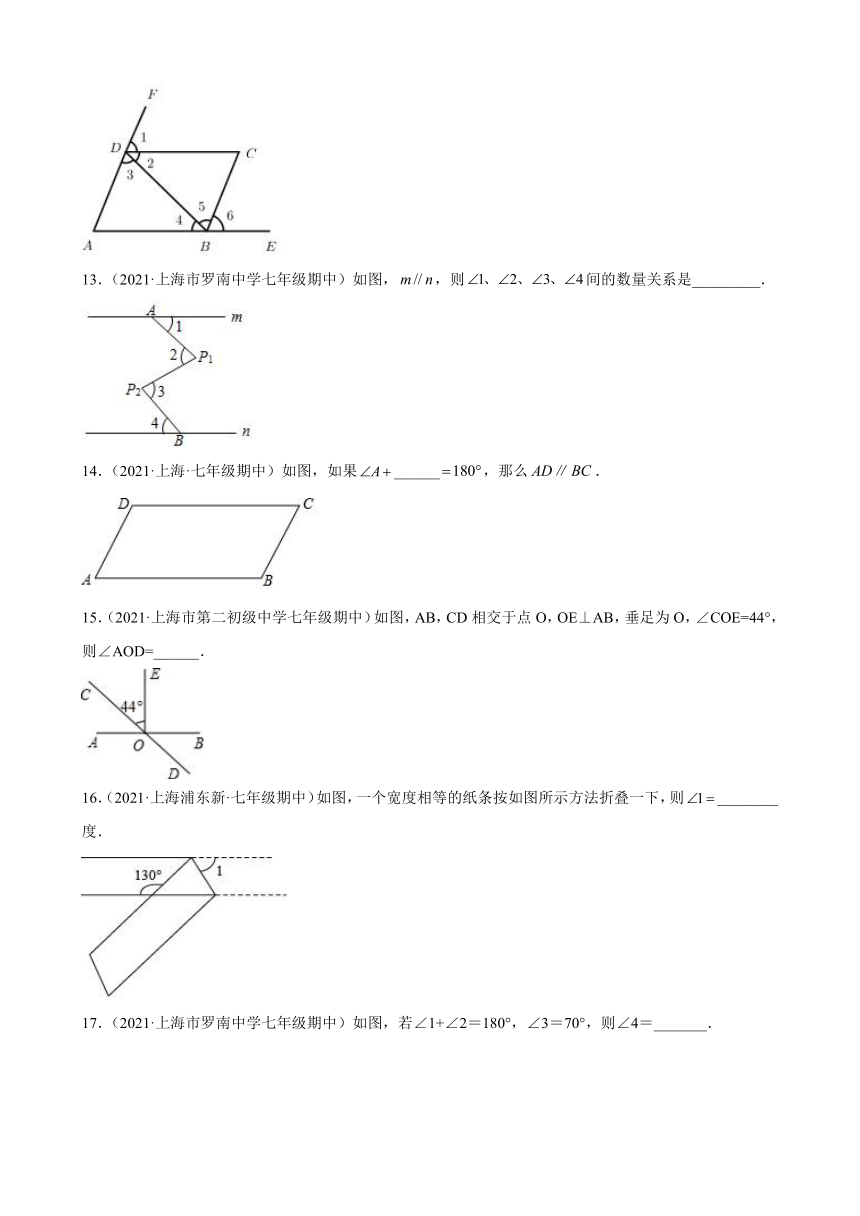
13.(2021·上海市罗南中学七年级期中)如图,,则间的数量关系是_________.
14.(2021·上海·七年级期中)如图,如果______,那么.
15.(2021·上海市第二初级中学七年级期中)如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD=______.
16.(2021·上海浦东新·七年级期中)如图,一个宽度相等的纸条按如图所示方法折叠一下,则________度.
17.(2021·上海市罗南中学七年级期中)如图,若∠1+∠2=180°,∠3=70°,则∠4=_______.
18.(2021·上海市罗南中学七年级期中)如图,直线AB和CD相交于点O,∠BOE=90°,∠DOE=130°,则∠AOC=______.
19.(2021·上海·七年级期中)如图,直线、被直线、所截,如果,,那么度数为_______.
20.(2021·上海市浦东新区新场实验中学七年级期中)如图,已知,则之间的数量关系是 _________
21.(2021·上海松江·七年级期中)如图,已知直线a、b被直线l所截,a∥b,且∠1=(3x+16)°,∠2=(2x﹣11)°,那么∠1=___度.
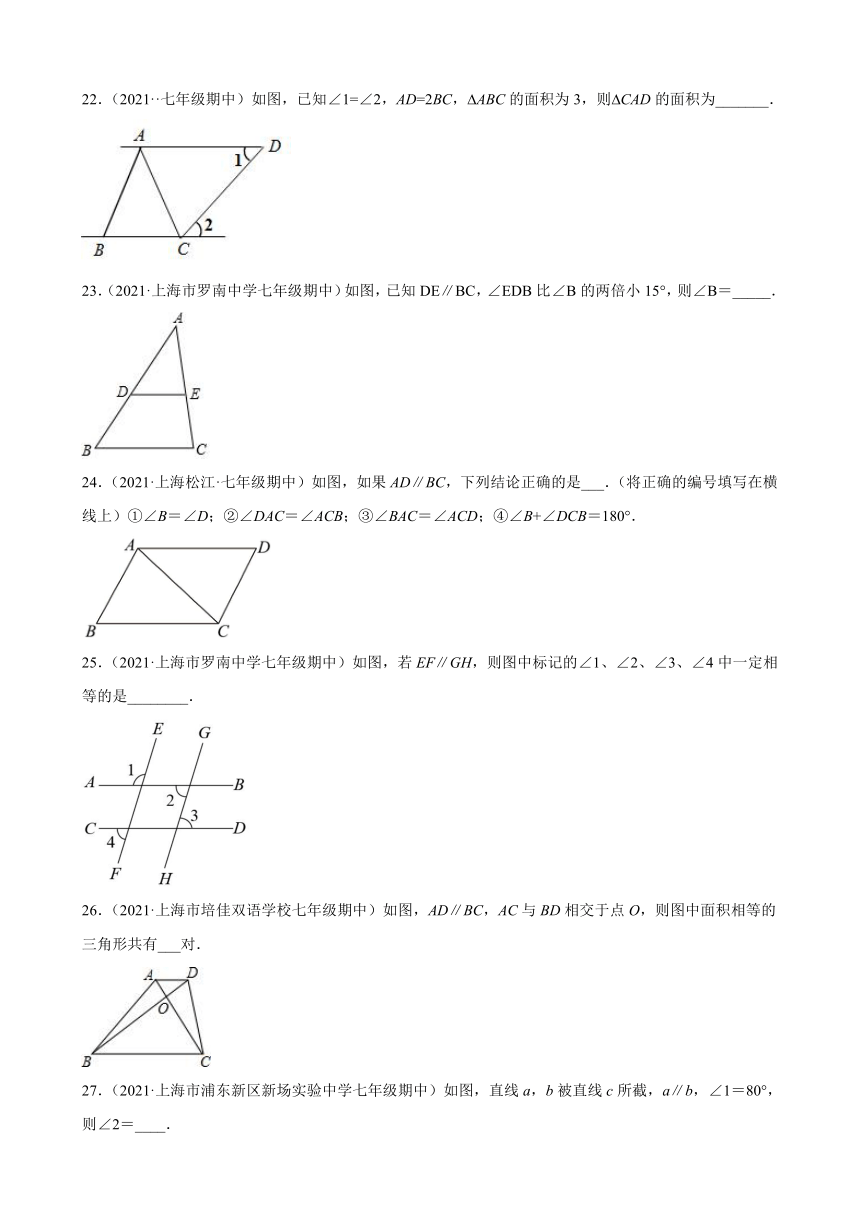
22.(2021··七年级期中)如图,已知∠1=∠2,AD=2BC, ABC的面积为3,则 CAD的面积为_______.
23.(2021·上海市罗南中学七年级期中)如图,已知DE∥BC,∠EDB比∠B的两倍小15°,则∠B=_____.
24.(2021·上海松江·七年级期中)如图,如果AD∥BC,下列结论正确的是___.(将正确的编号填写在横线上)①∠B=∠D;②∠DAC=∠ACB;③∠BAC=∠ACD;④∠B+∠DCB=180°.
25.(2021·上海市罗南中学七年级期中)如图,若EF∥GH,则图中标记的∠1、∠2、∠3、∠4中一定相等的是________.
26.(2021·上海市培佳双语学校七年级期中)如图,AD∥BC,AC与BD相交于点O,则图中面积相等的三角形共有___对.
27.(2021·上海市浦东新区新场实验中学七年级期中)如图,直线a,b被直线c所截,a∥b,∠1=80°,则∠2=____.
28.(2021·上海浦东新·七年级期中)如图,已知AB∥CD,∠ABC=120°,∠1=27°,则直线CB和CE的夹角是_____°.
29.(2021·上海·七年级期中)如图,已知长方形纸带,,,,,将纸带沿折叠后,点、分别落在、的位置,则下列结论中,正确的序号是_______.
①;②;③;④.
30.(2021·上海市风华初级中学七年级期中)如图,直线AC与直线DE相交于点O,若,,垂足为O,则______°.
31.(2021·上海市建平实验中学七年级期中)如图,已知AD∥BC,BE平分∠CBD,∠D=110°,那∠EBC的度数是_____.
32.(2021·上海杨浦·七年级期中)现有一张长方形纸片ABCD,将它按如图所示的方式进行折叠,如果∠BHG=50°,那么∠BHE的度数为______.
33.(2021·上海杨浦·七年级期中)如图,已知直线AD∥BC,如果△BCD的面积是6平方厘米,BC=4厘米,那么△ABC中BC边上的高是___厘米.
34.(2021·上海杨浦·七年级期中)如图,已知a∥b,如果∠1=70°,∠2=35°,那么∠3=_____度.
35.(2021·上海市第二初级中学七年级期中)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是________
36.(2021·上海市建平实验中学七年级期中)如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:____________(把你认为正确的序号填在空格内).
37.(2021··七年级期中)如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是__________
38.(2021··七年级期中)如图,直线AB,CD相交于点O.若∠BOD=40°,OA平分∠COE,则∠DOE=______.
39.(2021·上海浦东新·七年级期中)如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠ABC的补角,则∠BAH的度数是______.
40.(2021·上海松江·七年级期中)如图,已知点B在线段CF上,AB∥CD,AD∥BC,DF交AB于点E,联结AF、CE,S△BCE:S△AEF的比值为___.
41.(2021·上海·七年级期中)如图,平分,,,则__.
42.(2021·上海市川沙中学南校七年级期中)如图,DB平分∠ABC, AD//BC,若∠1=(2x+20)°,∠2=(4x+60)° ,则∠2= _________
43.(2021·上海浦东新·七年级期中)如图,在四边形BCEF中,BF∥AD∥CE,S△ABC=3,则△DEF的面积是___.
44.(2021·上海市文来中学七年级期中)9条不重合的直线相交于一点,构成的对顶角共有______对.
45.(2021·上海市建平实验中学七年级期中)如果∠1和∠2有公共顶点,且∠1的两边分别垂直于∠2的两边,若∠1=35°时,则∠2=_______.
46.(2021·上海杨浦·七年级期中)如图,已知AB∥CD,如果∠1=100°,∠2=120°,那么∠3=_____度.
47.(2021·上海·七年级期中)如图,直线a∥b,AC⊥AB,∠1=60°,则∠2的度数是________.
48.(2021·上海市风华初级中学七年级期中)如图,AB平分∠FEG,CD∥EG,∠BCD=(100+x)°,∠BEF=(140 x)°,那么∠ACD=______°.
试卷第1页,共3页
参考答案:
1.
【解析】
同位角的含义:若两个角在截线的同旁,都在被截线的同侧,则这两个角为同位角,根据此含义即可判断.
由图知:与∠A都是同位角
故答案为:
【点睛】
本题考查了同位角的识别,关键是掌握同位角的含义并能在图中正确识别.
2.②③⑤
【解析】
根据同位角、内错角、同旁内角的定义判断即可.
①中∠GBD和∠HCE没有任何关系,故①错;
②中∠ABD和∠ACH是直线FD与直线CH被直线AC所截形成的同位角,故②对;
③中∠FBC和∠ACE是直线FD与直线CE被直线AC所截形成的内错角,故③对;
④中∠FBC和∠HCE没有任何关系,故④错;
⑤中∠GBC和∠BCE是直线BG与直线CE被直线AC所截形成的同旁内角,故⑤对;
综上正确的有:②③⑤.
【点睛】
本题主要考查同位角、内错角、同旁内角的定义,解题的关键是能够熟练地掌握同位角、内错角、同旁内角的定义即可.
3.##∠BAE
【解析】
根据内错角的意义,结合具体的图形进行判断即可.
解:由内错角的意义可得,与是内错角,
故答案为:.
【点睛】
本题考查内错角,掌握内错角的意义是正确解答的前提.
4.2
【解析】
由题意直接根据同位角的定义进行解答即可.
解:根据同位角的定义可得:∠BAD和∠E是同位角;∠BAC和∠E是同位角;
∴∠E的同位角有2个.
故答案为:2.
【点睛】
本题考查同位角的概念,熟记同位角的定义是解题的关键.
5. 相交, 平行
【解析】
同一平面内,直线的位置关系通常有两种:平行或相交.
解:平面内的直线有平行或相交两种位置关系.
故答案为相交,平行.
【点睛】
本题主要考查了在同一平面内的两条直线的位置关系,属于基础题,应熟记这一知识点.
6. DE BC
【解析】
根据角平分线定义求出∠CDE,求出∠C+∠CDE=180°,根据平行线的判定推出即可.
∵DF平分∠CDE,∠CDF=55°,
∴∠CDE=2∠CDF=110°,
∵∠C=70°,
∴∠C+∠CDE=180°,
∴DE∥BC.
故答案为:(1)DE; (2)BC.
【点睛】
本题考查了平行线的判定,角平分线定义的应用,能求出∠C+∠CDE=180°是解此题的关键.
7.∠ABD=∠BDC或∠ABC+∠C=180°或∠BAD+∠ADC=180°(答案不唯一)
【解析】
根据平行线的判定,可利用内错角相等或同旁内角互补,可得出答案.
解:根据平行线的判定,可添加∠ABD=∠BDC,或∠ABC+∠C=180°,或∠BAD+∠ADC=180°,
故答案为:∠ABD=∠BDC,或∠ABC+∠C=180°,或∠BAD+∠ADC=180°,(填写一个即可).
【点睛】
本题主要考查平行线的判定,掌握平行线的判定方法是解题的关键.
8.110
【解析】
先根据角平分线的定义,求出∠BOC的度数,再根据对顶角相等求解即可.
解:∵OE平分∠BOC,∠BOE=55°,
∴∠BOC=2∠BOE=2×55°=110°,
∴∠AOC=∠BOC=110°.
故答案为:110.
【点睛】
本题考查了角平分线的定义以及对顶角相等,是基础题,比较简单.
9.①②④
【解析】
根据平行线的判定定理判断①;根据角的关系判断②即可;根据平行线的性质定理判断③;根据①的结论和平行线的性质定理判断④.
∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC//DE,故①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,故②正确;
∵BC//AD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90° 45°=45°,故③错误;
∵∠D=30°,∠CAD=150°,
∴∠CAD+∠D=180°,
∴AC//DE,
∴∠4=∠C,故④正确.
故答案为①②④
【点睛】
此题考查平行线的判定定理和性质,角的关系,解题关键在于利用判定定理进行判断
10.4
【解析】
根据同旁内角定义:两条直线被第三条直线所截,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,进行分析即可.
解:∠1和∠2,∠1和∠3,∠2和∠3,∠4和∠5是同旁内角,共4对,
故答案为:4.
【点睛】
此题主要考查了同旁内角的定义,关键是掌握同旁内角的边构成“U”形.
11.40°
【解析】
根据邻补角互补可得∠AOC的度数,进而可得答案.
解:∵∠AOD=140°,
∴∠AOC=180°﹣140°=40°,
∴直线AB与CD的夹角是40°.
故答案为:40°.
【点睛】
此题主要考查了邻补角,关键是掌握邻补角互补,对顶角相等.
12. ##DA ##CB
【解析】
与是内错角,根据“内错角相等,两直线平行”可以得到.
解:∵(已知)
∴(内错角相等,两直线平行)
【点睛】
本题考查了平行线的判定,熟练判断三线八角是解题关键.
13.∠2+∠4=∠1+∠3
【解析】
分别过点P1、P2作P1C∥m,P2D∥m,由平行线的性质可知,∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,所以∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,
∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
【点睛】
本题考查的是平行线的性质,即两直线平行,内错角相等.
14.##∠ABC##∠CBA
【解析】
根据平行线的判定定理即可得到结论.
解:,
.
故答案为.
【点睛】
本题考查了平行线的判定定理,熟练掌握同旁内角互补两直线平行是解题的关键.
15.134°
【解析】
解:∵OE⊥AB,
∴∠AOE=90°,
∵∠COE=44°,
∴∠AOC=46°,
∴∠AOD=180°-∠AOC=180°-46°=134°,
故答案为:134°.
16.65
【解析】
根据两直线平行内错角相等,以及折叠关系列出方程求解则可.
解:如图,由题意可知,
由题意知ABCD,
∴∠1+∠2=130°,
由折叠可知,∠1=∠2,
∴2∠1=130°,
解得∠1=65°.
故答案为:65.
【点睛】
本题考查了平行线的性质和折叠的知识,根据折叠得出∠1=∠2是解题的关键.
17.
【解析】
如图(见解析),先根据平行线的判定可得,再根据平行线的性质可得,然后根据邻补角的定义即可得.
解:如图,,
,
,
,
,
故答案为:.
【点睛】
本题考查了平行线的判定与性质、邻补角,熟练掌握平行线的判定与性质是解题关键.
18.40°##40度
【解析】
先根据角的和差关系可求∠BOD,再根据对顶角相等可求∠AOC.
解:∵∠BOE=90°,∠DOE=130°,
∴∠BOD=130°-90°=40°,
又
∴∠AOC=40°.
故答案为:40°.
【点睛】
本题考查了对顶角,关键是根据角的和差关系可求∠BOD.
19.##75度
【解析】
求出,根据平行线的判定得出直线直线,根据平行线的性质得出即可.
解:,
,
,
直线直线,
,
故答案为:.
【点睛】
本题考查了平行线的判定和性质,能求出直线直线是解此题的关键.
20.
【解析】
由平行线的性质得出和,从而可得出结论.
故答案为:.
【点睛】
本题主要考查平行线的性质,掌握平行线的性质是解题的关键.
21.121
【解析】
根据两直线平行同旁内角互补列方程求解.
解:∵a//b,
∴∠1+∠2=180°,
(3x+16)+(2x﹣11)=180,
解得x=35,
∴∠1=(3×35+16)°=121°,
故答案为:121.
【点睛】
本题考查了平行线的性质,一元一次方程的应用,根据题意列出方程求出x是解答本题的关键.
22.6
【解析】
首先根据内错角相等判定AD//BC,过点C作CM⊥AD,AN⊥BC,即可得出CM=AN,进而得出△ACD和△ABC的面积关系,即可得解.
∵∠1=∠2
∴AD//BC,
过点C作CM⊥AD,AN⊥BC,如图所示:
∴CM=AN
∵
,
故答案为:6.
【点睛】
此题主要考查平行线的判定与性质,熟练掌握,即可解题.
23.##65度
【解析】
根据平行线的性质和题意,列出关系式求解即可.
解:∵DE∥BC,
∴∠B+∠EDB=180°,
∵2∠B﹣∠EDB=15°,
∴3∠B=195°,
∴∠B=65°,
故答案为:.
【点睛】
本题考查的是平行线的性质和列关系式,能根据题意,准确列出关系式是解题的关键.
24.②
【解析】
根据AD∥BC,利用平行线的性质逐一推理即可找出答案.
解:∵AD∥BC,
∴∠DAC=∠ACB(两直线平行,内错角相等),
故②正确,
①、③、④由AD∥BC无法求证,故①、③、④错误,
故答案为:②.
【点睛】
本题考查平行线的性质,熟练掌握平行线形成角的关系是解题关键.
25.
【解析】
如图(见解析),先根据对顶角相等可得,再根据平行线的性质可得,由此即可得出答案.
解:如图,由对顶角相等得:,
,
,
,
故答案为:.
【点睛】
本题考查了对顶角相等、平行线的性质,熟练掌握平行线的性质是解题关键.
26.3
【解析】
根据平行线的性质可得到两对同底同高的三角形,△AOB与△DOC由△ADC与△DAB减去△ADO得到,故面积相等的三角形有三对.
解:根据平行线的性质知,△ADC与△DAB,△ABC与DCB都是同底等高的三角形,△AOB与△DOC由△ADC与△DAB减去△ADO得到,
所以面积相等的三角形有三对,
故答案为:3.
【点睛】
本题考查了平行线间的距离,三角形的面积的公式,熟记平行线间的距离处处相等是解题的关键.
27.100°
【解析】
由对顶角相等可求出∠3的度数,由a∥b,利用“两直线平行,同旁内角互补”可求出∠2的度数.
∵∠1=80°,
∴∠3=80°.
∵a∥b,
∴∠2+∠3=180°,
∴∠2=180°﹣80°=100°.
故答案为:100°.
.
【点睛】
本题考查了平行线的性质,牢记“两直线平行,同旁内角互补”是解题的关键.
28.93
【解析】
AB∥CD,∠DCB=∠ABC=120°,将角度代入∠BCE=∠DCB -∠1求解即可.
解:∵AB∥CD
∴∠DCB=∠ABC=120°
又∵∠1=27°
∴∠BCE=∠DCB -∠1=93°
故答案为93.
【点睛】
本题考查了平行线中关于内错角的性质.解题的关键在于熟练使用两直线平行,内错角相等的性质.
29.①③④
【解析】
根据两直线平行,内错角相等可判断①,根据平行线的性质,折叠性质,利用角的和差判断④,根据平角定义及折叠性质可判断②,根据平角定义可判断③.
解:四边形是长方形,
,,
,
,①正确;
,
,
由折叠得,,,,,
,④正确;
,
,
,
,②错误;
,
,③正确.
故答案为:①③④.
【点睛】
本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.
30.55
【解析】
先根据垂直的定义求出,再由对顶角相等求解即可.
解:∵,
∴,
∴,
∴,
故答案为:55.
【点睛】
本题主要考查了垂直的定义,对顶角相等,熟知相关知识是解题的关键.
31.35°
【解析】
先根据平行线的性质,求出∠DBC=180°-∠D=70°,再根据角平分线的性质得到.
解:∵AD∥BC,
∴∠D+∠DBC=180°,
∵∠D=110°,
∴∠DBC=180°-∠D=70°,
∵BE平分∠DBC,
∴,
故答案为:35°.
【点睛】
本题主要考查了平行线的性质,角平分线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
32.65°
【解析】
根据四边形是长方形,可得,根据平行线的性质可得,,再根据折叠可得,,等量代换后即可得结果.
解:四边形是长方形,
,
,,
根据折叠可知:
,
,
,
,
.
故答案为:.
【点睛】
本题考查了平行线的性质,解决本题的关键是熟练掌握平行线的性质.
33.3
【解析】
根据平行线之间的距离处处相等可得答案.
解:因为△BCD的面积是6平方厘米,BC=4厘米,
所以BC边上的高是:2×6÷4=3(厘米).
故答案为:3.
【点睛】
本题主要考查了平行线间的距离,准确计算是解题的关键.
34.75
【解析】
根据平行线的性质和的度数得到,再利用平角的性质可得的度数.
解:如图:
,,
.
,
.
故答案为:75.
【点睛】
此题考查了平行线的性质,解题的关键是注意掌握两直线平行,同位角相等定理的应用.
35.15°##15度
【解析】
如下图,过点E作EFBC,然后利用平行线的性质结合已知条件进行分析解答即可.
由题意可得ADBC,∠DAE=∠1+45°,∠AEB=90°,∠EBC=30°,过点E作EFBC,
则ADEFBC,
∴∠AEF=∠DAE=∠1+45°,∠FEB=∠EBC=30°,
又∵∠AEF=∠AEB-∠FEB,
∴∠AEF=90°-30°=60°,
∴∠1+45°=60°,
∴∠1=60°-45°=15°.
故答案为:15°.
36.①②③④
【解析】
根据平行线的判定方法:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行进行分析即可.
①∠1=∠2可根据同位角相等,两直线平行得到a∥b;
②∠3=∠6可根据内错角相等,两直线平行得到a∥b;
③若∠1=∠8,则∠2=∠7可根据内错角相等,两直线平行得到a∥b;
④∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b;
故答案为①②③④.
【点睛】
本题考查平行线的判定,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,解题的关键是搞清楚同位角、内错角、同旁内角的概念
37.150°
【解析】
过点B作BE∥AD,
∵AD∥CF,
∴BE∥AD∥CF,
∴∠1=∠A=120°,∠2+∠C=180°,
∵∠ABC=150°,∠1+∠2=∠ABC,
∴∠2=30°,
∴∠C=150°.
38.100°
【解析】
利用对顶角相等即可求得∠AOC的度数,然后根据角平分线的定义求得∠COE的度数,然后根据∠COE和∠EOD互补即可求解.
解:∵∠AOC=∠BOD=40°,
又∵OA平分∠COE,
∴∠COE=2∠AOC=80°,
∴∠EOD=180°-∠COE=180°-80°=100°.
故答案为100°.
【点睛】
本题考查邻补角的定义,对顶角的性质,角平分线的定义,是一个基础题.
39.60°##60度
【解析】
设∠BAF=x°,∠BCF=y°,由题意知∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,如图,过点B作BM∥AD,过点F作FN∥AD,由AD∥CE可得AD∥FN∥BM∥CE,有∠AFN=∠HAF=x°,∠CFN=∠GCF=2y°,ABM=∠BAH=2x°,∠CBM=∠GCB=y°,∠AFC=(x+2y)°,∠ABC=(2x+y)°由于∠F的余角等于2∠B的补角,可知90﹣(x+2y)=180﹣2(2x+y),进行求解可得x的值,进而可求出∠BAH的值.
解:设∠BAF=x°,∠BCF=y°
∵∠BCF=∠BCG,CF与∠BAH的平分线交于点F
∴∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,
如图,过点B作BM∥AD,过点F作FN∥AD
∵AD∥CE
∴AD∥FN∥BM∥CE
∴∠AFN=∠HAF=x°,∠CFN=∠GCF=2y°,∠ABM=∠BAH=2x°,∠CBM=∠GCB=y°
∴∠AFC=(x+2y)°,∠ABC=(2x+y)°
∵∠AFC的余角等于2∠ABC的补角
∴90﹣(x+2y)=180﹣2(2x+y)
解得:x=30
∴∠BAH=60°
故答案为:60°.
【点睛】
本题考查了角平分线,平行线的性质,余角、补角等知识.解题的关键在于正确的表示角度之间的数量关系.
40.1
【解析】
连接BD,利用平行线间距离相等得到同底等高的三角形面积相等即可解答.
解:连接BD,如下图所示:
∵BC∥AD,
∴S△AFD= S△ABD,
∴S△AFD- S△AED= S△ABD- S△AED,
即S△AEF= S△BED,
∵AB∥CD,
∴S△BED=S△BEC,
∴S△AEF=S△BEC,
∴S△BCE:S△AEF=1.
故答案为:1.
【点睛】
本题以平行为背景考查了同底等高的三角形面积相等,找到要求的三角形有关的同(等)底或同(等)高是解题的关键.
41.##BC//DE
【解析】
由平分,可得,再根据同旁内角互补两直线平行可得结论.
解:平分,,
∴=2=110°,
,
∴∠C+∠CDE=70°+110°=180°,
.
故答案为:.
【点睛】
本题考查了角的平分线的性质,平行线的判定,熟练的掌握平行线的判定方法是解题关键.
42.100°
【解析】
根据AD//BC可得,∠1=∠ADB,△ABD的内角和为180°,即可求出∠2的度数.
解:∵AD//BC,∴∠1=∠ADB,在△ABD中,∠1+∠2+∠ADB=2∠1+∠2=180°,求出x=10,∠2=(4x+60)°=100°,故答案为100°.
【点睛】
此题考查了平行线的性质和三角形内角和定理,熟练掌握定理是解题的关键.
43.6
【解析】
根据题意利用平行线间距离即所有垂线段的长度相等,可以求得S△ADF=S△ABD,S△ADE=S△ACD,S△CEF=S△BCE,利用面积相等把S△DEF转化为已知△ABC的面积,即可求解.
解:∵BF∥AD∥CE,
∴S△ADF=S△ABD,S△ADE=S△ACD,S△CEF=S△BCE,
∴S△AEF=S△CEF-S△ACE=S△BCE-S△ACE=S△ABC,
S△DEF=S△ADF+S△ADE+S△AEF=S△ABD+S△ACD+S△ABC=S△ABC+S△ABC=2S△ABC=2×3=6,
故答案为:6.
【点睛】
本题考查平行线的推论,注意掌握平行线间距离即所有垂线段的长度相等并利用三角形面积相等,把S△DEF转化为已知△ABC的面积.
44.72
【解析】
本题考查对顶角的定义,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.
解:①两条直线相交共2对对顶角;
②三条直线相交,在2对的基础上再加4对,共6对;
③四条直线相交,在6对的基础上再加6对,共12对;
④五条直线相交,在12对的基础上再加8对,共20对;
即对顶角的对数为,2,6,12,20……,
以此类推,当n条直线相交时,对顶角的总对数为: ;
根据n条直线相交于一点,构成对对顶角的规律可知,
当时,=(92-9)=72(对),
故答案为:72.
【点睛】
本题考查了对顶角的定义及n条直线相交于一点,构成对顶角的规律,注意对顶角是两条直线相交而成的四个角中,没有公共边的两个角.
45.35°或145°
【解析】
分∠1在∠2内部和外部两种情况,画出图形,根据角的和差关系即可得答案.
如图,当∠1在∠2外部时,
∵∠1的两边分别垂直于∠2的两边,
∴∠AOC=∠BOD=90°,
∴∠1+∠BOC=∠2+∠BOC,
∴∠2=∠1=35°.
如图,当∠1在∠2内部时,
∵∠1的两边分别垂直于∠2的两边,
∴∠AOD=∠BOC=90°,
∴∠AOC=∠BOD=90°-∠1=90°-35°=55°,
∴∠2=∠AOC+∠1+∠BOD=55°+35°+55°=145°.
故答案为:35°或145°
【点睛】
本题考查角的运算,分情况正确画出图形是解题关键.
46.40
【解析】
过作平行于,由与平行,得到与平行,利用两直线平行同位角相等,同旁内角互补,得到,,即可确定出的度数.
解:如图:过作平行于,
,
,
,
,即,
.
故答案为:40.
【点睛】
此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
47.30°
【解析】
根据平行线的性质,可得∠3与∠1的关系,根据两直线垂直,可得所成的角是90°,根据角的和差,可得答案.
解:如图所示:
,
∵直线a∥b,
∴∠3=∠1=60°.
∵AC⊥AB,
∴∠3+∠2=90°,
∴∠2=90°-∠3=90°-60°=30°,
故答案是:30°.
【点睛】
本题考查了平行线的性质,解题的关键是利用了平行线的性质,垂线的性质,角的和差.
48.60
【解析】
根据角平分线的定义、平行线的性质以及平角的定义得到∠BCD=∠BEF,列出方程求解即可.
解:∵AB平分∠FEG,
∴∠AEG=∠AEF,
∵∠AEF=180° ∠BEF,
∴∠AEG=180° ∠BEF,
∵CD∥BG,
∴∠AEG=∠ACD,
∴∠ACD=180° ∠BEF,
∵∠ACD+∠BCD=180°,
∴180° ∠BEF+∠BCD=180°,
∴∠BCD=∠BEF,
∵∠BCD=(100+x)°,∠BEF=(140 x)°,
∴(100+x)°=(140 x)°,
∴100+x=140 x,
∴x=20,
∴∠BCD=(100+20)°=120°,
∴∠ACD=180° ∠BCD=180° 120°=60°,
故答案为:60.
【点睛】
本题考查了平行线与角平分线的性质,解一元一次方程,解题关键是熟练掌握平行线与角平分线的性质.
答案第1页,共2页
1.(2021·上海松江·七年级期中)如图,和∠A是同位角的有___.
2.(2021·上海市罗南中学七年级期中)如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是____.(填序号)
3.(2021·上海·七年级期中)如图,射线,相交于点,则的内错角是__.
4.(2021·上海浦东新·七年级期中)如图,∠E的同位角有___个.
5.(2021·上海市罗南中学七年级期中)在同一平面内,两条不相重合的直线位置关系有两种:_____和_____.
6.(2021·上海市浦东新区新场实验中学七年级期中)如图,平分,,,则________∥________
7.(2021·上海市南洋模范初级中学七年级期中)如图,添加一个条件使,这个条件可以是______(只需写出一种情况)
8.(2021·上海杨浦·七年级期中)如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=55°,那么∠AOD=______度.
9.(2021·上海市民办文绮中学七年级期中)将一副三角板按如图放置,小明得到下列结论:①如果∠2=30°,则有AC∥DE;②∠BAE+∠CAD=180°;③如果BC∥AD,则有∠2=30°;④如果∠CAD=150°,则∠4=∠C;那么其中正确的结论有________
10.(2021·上海市教育学会青浦清河湾中学七年级期中)如图,同旁内角有_______________对.
11.(2021·上海杨浦·七年级期中)如图,直线AB、CD相交于点O,如果∠AOD=140°,那么直线AB与CD的夹角是______.
12.(2021·上海市第二初级中学七年级期中)如图,已知,那么____________.
13.(2021·上海市罗南中学七年级期中)如图,,则间的数量关系是_________.
14.(2021·上海·七年级期中)如图,如果______,那么.
15.(2021·上海市第二初级中学七年级期中)如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD=______.
16.(2021·上海浦东新·七年级期中)如图,一个宽度相等的纸条按如图所示方法折叠一下,则________度.
17.(2021·上海市罗南中学七年级期中)如图,若∠1+∠2=180°,∠3=70°,则∠4=_______.
18.(2021·上海市罗南中学七年级期中)如图,直线AB和CD相交于点O,∠BOE=90°,∠DOE=130°,则∠AOC=______.
19.(2021·上海·七年级期中)如图,直线、被直线、所截,如果,,那么度数为_______.
20.(2021·上海市浦东新区新场实验中学七年级期中)如图,已知,则之间的数量关系是 _________
21.(2021·上海松江·七年级期中)如图,已知直线a、b被直线l所截,a∥b,且∠1=(3x+16)°,∠2=(2x﹣11)°,那么∠1=___度.
22.(2021··七年级期中)如图,已知∠1=∠2,AD=2BC, ABC的面积为3,则 CAD的面积为_______.
23.(2021·上海市罗南中学七年级期中)如图,已知DE∥BC,∠EDB比∠B的两倍小15°,则∠B=_____.
24.(2021·上海松江·七年级期中)如图,如果AD∥BC,下列结论正确的是___.(将正确的编号填写在横线上)①∠B=∠D;②∠DAC=∠ACB;③∠BAC=∠ACD;④∠B+∠DCB=180°.
25.(2021·上海市罗南中学七年级期中)如图,若EF∥GH,则图中标记的∠1、∠2、∠3、∠4中一定相等的是________.
26.(2021·上海市培佳双语学校七年级期中)如图,AD∥BC,AC与BD相交于点O,则图中面积相等的三角形共有___对.
27.(2021·上海市浦东新区新场实验中学七年级期中)如图,直线a,b被直线c所截,a∥b,∠1=80°,则∠2=____.
28.(2021·上海浦东新·七年级期中)如图,已知AB∥CD,∠ABC=120°,∠1=27°,则直线CB和CE的夹角是_____°.
29.(2021·上海·七年级期中)如图,已知长方形纸带,,,,,将纸带沿折叠后,点、分别落在、的位置,则下列结论中,正确的序号是_______.
①;②;③;④.
30.(2021·上海市风华初级中学七年级期中)如图,直线AC与直线DE相交于点O,若,,垂足为O,则______°.
31.(2021·上海市建平实验中学七年级期中)如图,已知AD∥BC,BE平分∠CBD,∠D=110°,那∠EBC的度数是_____.
32.(2021·上海杨浦·七年级期中)现有一张长方形纸片ABCD,将它按如图所示的方式进行折叠,如果∠BHG=50°,那么∠BHE的度数为______.
33.(2021·上海杨浦·七年级期中)如图,已知直线AD∥BC,如果△BCD的面积是6平方厘米,BC=4厘米,那么△ABC中BC边上的高是___厘米.
34.(2021·上海杨浦·七年级期中)如图,已知a∥b,如果∠1=70°,∠2=35°,那么∠3=_____度.
35.(2021·上海市第二初级中学七年级期中)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是________
36.(2021·上海市建平实验中学七年级期中)如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:____________(把你认为正确的序号填在空格内).
37.(2021··七年级期中)如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是__________
38.(2021··七年级期中)如图,直线AB,CD相交于点O.若∠BOD=40°,OA平分∠COE,则∠DOE=______.
39.(2021·上海浦东新·七年级期中)如图,已知AD∥CE,∠BCF=∠BCG,CF与∠BAH的平分线交于点F,若∠AFC的余角等于2∠ABC的补角,则∠BAH的度数是______.
40.(2021·上海松江·七年级期中)如图,已知点B在线段CF上,AB∥CD,AD∥BC,DF交AB于点E,联结AF、CE,S△BCE:S△AEF的比值为___.
41.(2021·上海·七年级期中)如图,平分,,,则__.
42.(2021·上海市川沙中学南校七年级期中)如图,DB平分∠ABC, AD//BC,若∠1=(2x+20)°,∠2=(4x+60)° ,则∠2= _________
43.(2021·上海浦东新·七年级期中)如图,在四边形BCEF中,BF∥AD∥CE,S△ABC=3,则△DEF的面积是___.
44.(2021·上海市文来中学七年级期中)9条不重合的直线相交于一点,构成的对顶角共有______对.
45.(2021·上海市建平实验中学七年级期中)如果∠1和∠2有公共顶点,且∠1的两边分别垂直于∠2的两边,若∠1=35°时,则∠2=_______.
46.(2021·上海杨浦·七年级期中)如图,已知AB∥CD,如果∠1=100°,∠2=120°,那么∠3=_____度.
47.(2021·上海·七年级期中)如图,直线a∥b,AC⊥AB,∠1=60°,则∠2的度数是________.
48.(2021·上海市风华初级中学七年级期中)如图,AB平分∠FEG,CD∥EG,∠BCD=(100+x)°,∠BEF=(140 x)°,那么∠ACD=______°.
试卷第1页,共3页
参考答案:
1.
【解析】
同位角的含义:若两个角在截线的同旁,都在被截线的同侧,则这两个角为同位角,根据此含义即可判断.
由图知:与∠A都是同位角
故答案为:
【点睛】
本题考查了同位角的识别,关键是掌握同位角的含义并能在图中正确识别.
2.②③⑤
【解析】
根据同位角、内错角、同旁内角的定义判断即可.
①中∠GBD和∠HCE没有任何关系,故①错;
②中∠ABD和∠ACH是直线FD与直线CH被直线AC所截形成的同位角,故②对;
③中∠FBC和∠ACE是直线FD与直线CE被直线AC所截形成的内错角,故③对;
④中∠FBC和∠HCE没有任何关系,故④错;
⑤中∠GBC和∠BCE是直线BG与直线CE被直线AC所截形成的同旁内角,故⑤对;
综上正确的有:②③⑤.
【点睛】
本题主要考查同位角、内错角、同旁内角的定义,解题的关键是能够熟练地掌握同位角、内错角、同旁内角的定义即可.
3.##∠BAE
【解析】
根据内错角的意义,结合具体的图形进行判断即可.
解:由内错角的意义可得,与是内错角,
故答案为:.
【点睛】
本题考查内错角,掌握内错角的意义是正确解答的前提.
4.2
【解析】
由题意直接根据同位角的定义进行解答即可.
解:根据同位角的定义可得:∠BAD和∠E是同位角;∠BAC和∠E是同位角;
∴∠E的同位角有2个.
故答案为:2.
【点睛】
本题考查同位角的概念,熟记同位角的定义是解题的关键.
5. 相交, 平行
【解析】
同一平面内,直线的位置关系通常有两种:平行或相交.
解:平面内的直线有平行或相交两种位置关系.
故答案为相交,平行.
【点睛】
本题主要考查了在同一平面内的两条直线的位置关系,属于基础题,应熟记这一知识点.
6. DE BC
【解析】
根据角平分线定义求出∠CDE,求出∠C+∠CDE=180°,根据平行线的判定推出即可.
∵DF平分∠CDE,∠CDF=55°,
∴∠CDE=2∠CDF=110°,
∵∠C=70°,
∴∠C+∠CDE=180°,
∴DE∥BC.
故答案为:(1)DE; (2)BC.
【点睛】
本题考查了平行线的判定,角平分线定义的应用,能求出∠C+∠CDE=180°是解此题的关键.
7.∠ABD=∠BDC或∠ABC+∠C=180°或∠BAD+∠ADC=180°(答案不唯一)
【解析】
根据平行线的判定,可利用内错角相等或同旁内角互补,可得出答案.
解:根据平行线的判定,可添加∠ABD=∠BDC,或∠ABC+∠C=180°,或∠BAD+∠ADC=180°,
故答案为:∠ABD=∠BDC,或∠ABC+∠C=180°,或∠BAD+∠ADC=180°,(填写一个即可).
【点睛】
本题主要考查平行线的判定,掌握平行线的判定方法是解题的关键.
8.110
【解析】
先根据角平分线的定义,求出∠BOC的度数,再根据对顶角相等求解即可.
解:∵OE平分∠BOC,∠BOE=55°,
∴∠BOC=2∠BOE=2×55°=110°,
∴∠AOC=∠BOC=110°.
故答案为:110.
【点睛】
本题考查了角平分线的定义以及对顶角相等,是基础题,比较简单.
9.①②④
【解析】
根据平行线的判定定理判断①;根据角的关系判断②即可;根据平行线的性质定理判断③;根据①的结论和平行线的性质定理判断④.
∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC//DE,故①正确;
∵∠1+∠2=90°,∠2+∠3=90°,
即∠BAE+∠CAD=∠1+∠2+∠2+∠3=90°+90°=180°,故②正确;
∵BC//AD,
∴∠1+∠2+∠3+∠C=180°,
又∵∠C=45°,∠1+∠2=90°,
∴∠3=45°,
∴∠2=90° 45°=45°,故③错误;
∵∠D=30°,∠CAD=150°,
∴∠CAD+∠D=180°,
∴AC//DE,
∴∠4=∠C,故④正确.
故答案为①②④
【点睛】
此题考查平行线的判定定理和性质,角的关系,解题关键在于利用判定定理进行判断
10.4
【解析】
根据同旁内角定义:两条直线被第三条直线所截,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,进行分析即可.
解:∠1和∠2,∠1和∠3,∠2和∠3,∠4和∠5是同旁内角,共4对,
故答案为:4.
【点睛】
此题主要考查了同旁内角的定义,关键是掌握同旁内角的边构成“U”形.
11.40°
【解析】
根据邻补角互补可得∠AOC的度数,进而可得答案.
解:∵∠AOD=140°,
∴∠AOC=180°﹣140°=40°,
∴直线AB与CD的夹角是40°.
故答案为:40°.
【点睛】
此题主要考查了邻补角,关键是掌握邻补角互补,对顶角相等.
12. ##DA ##CB
【解析】
与是内错角,根据“内错角相等,两直线平行”可以得到.
解:∵(已知)
∴(内错角相等,两直线平行)
【点睛】
本题考查了平行线的判定,熟练判断三线八角是解题关键.
13.∠2+∠4=∠1+∠3
【解析】
分别过点P1、P2作P1C∥m,P2D∥m,由平行线的性质可知,∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,所以∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,
∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
【点睛】
本题考查的是平行线的性质,即两直线平行,内错角相等.
14.##∠ABC##∠CBA
【解析】
根据平行线的判定定理即可得到结论.
解:,
.
故答案为.
【点睛】
本题考查了平行线的判定定理,熟练掌握同旁内角互补两直线平行是解题的关键.
15.134°
【解析】
解:∵OE⊥AB,
∴∠AOE=90°,
∵∠COE=44°,
∴∠AOC=46°,
∴∠AOD=180°-∠AOC=180°-46°=134°,
故答案为:134°.
16.65
【解析】
根据两直线平行内错角相等,以及折叠关系列出方程求解则可.
解:如图,由题意可知,
由题意知ABCD,
∴∠1+∠2=130°,
由折叠可知,∠1=∠2,
∴2∠1=130°,
解得∠1=65°.
故答案为:65.
【点睛】
本题考查了平行线的性质和折叠的知识,根据折叠得出∠1=∠2是解题的关键.
17.
【解析】
如图(见解析),先根据平行线的判定可得,再根据平行线的性质可得,然后根据邻补角的定义即可得.
解:如图,,
,
,
,
,
故答案为:.
【点睛】
本题考查了平行线的判定与性质、邻补角,熟练掌握平行线的判定与性质是解题关键.
18.40°##40度
【解析】
先根据角的和差关系可求∠BOD,再根据对顶角相等可求∠AOC.
解:∵∠BOE=90°,∠DOE=130°,
∴∠BOD=130°-90°=40°,
又
∴∠AOC=40°.
故答案为:40°.
【点睛】
本题考查了对顶角,关键是根据角的和差关系可求∠BOD.
19.##75度
【解析】
求出,根据平行线的判定得出直线直线,根据平行线的性质得出即可.
解:,
,
,
直线直线,
,
故答案为:.
【点睛】
本题考查了平行线的判定和性质,能求出直线直线是解此题的关键.
20.
【解析】
由平行线的性质得出和,从而可得出结论.
故答案为:.
【点睛】
本题主要考查平行线的性质,掌握平行线的性质是解题的关键.
21.121
【解析】
根据两直线平行同旁内角互补列方程求解.
解:∵a//b,
∴∠1+∠2=180°,
(3x+16)+(2x﹣11)=180,
解得x=35,
∴∠1=(3×35+16)°=121°,
故答案为:121.
【点睛】
本题考查了平行线的性质,一元一次方程的应用,根据题意列出方程求出x是解答本题的关键.
22.6
【解析】
首先根据内错角相等判定AD//BC,过点C作CM⊥AD,AN⊥BC,即可得出CM=AN,进而得出△ACD和△ABC的面积关系,即可得解.
∵∠1=∠2
∴AD//BC,
过点C作CM⊥AD,AN⊥BC,如图所示:
∴CM=AN
∵
,
故答案为:6.
【点睛】
此题主要考查平行线的判定与性质,熟练掌握,即可解题.
23.##65度
【解析】
根据平行线的性质和题意,列出关系式求解即可.
解:∵DE∥BC,
∴∠B+∠EDB=180°,
∵2∠B﹣∠EDB=15°,
∴3∠B=195°,
∴∠B=65°,
故答案为:.
【点睛】
本题考查的是平行线的性质和列关系式,能根据题意,准确列出关系式是解题的关键.
24.②
【解析】
根据AD∥BC,利用平行线的性质逐一推理即可找出答案.
解:∵AD∥BC,
∴∠DAC=∠ACB(两直线平行,内错角相等),
故②正确,
①、③、④由AD∥BC无法求证,故①、③、④错误,
故答案为:②.
【点睛】
本题考查平行线的性质,熟练掌握平行线形成角的关系是解题关键.
25.
【解析】
如图(见解析),先根据对顶角相等可得,再根据平行线的性质可得,由此即可得出答案.
解:如图,由对顶角相等得:,
,
,
,
故答案为:.
【点睛】
本题考查了对顶角相等、平行线的性质,熟练掌握平行线的性质是解题关键.
26.3
【解析】
根据平行线的性质可得到两对同底同高的三角形,△AOB与△DOC由△ADC与△DAB减去△ADO得到,故面积相等的三角形有三对.
解:根据平行线的性质知,△ADC与△DAB,△ABC与DCB都是同底等高的三角形,△AOB与△DOC由△ADC与△DAB减去△ADO得到,
所以面积相等的三角形有三对,
故答案为:3.
【点睛】
本题考查了平行线间的距离,三角形的面积的公式,熟记平行线间的距离处处相等是解题的关键.
27.100°
【解析】
由对顶角相等可求出∠3的度数,由a∥b,利用“两直线平行,同旁内角互补”可求出∠2的度数.
∵∠1=80°,
∴∠3=80°.
∵a∥b,
∴∠2+∠3=180°,
∴∠2=180°﹣80°=100°.
故答案为:100°.
.
【点睛】
本题考查了平行线的性质,牢记“两直线平行,同旁内角互补”是解题的关键.
28.93
【解析】
AB∥CD,∠DCB=∠ABC=120°,将角度代入∠BCE=∠DCB -∠1求解即可.
解:∵AB∥CD
∴∠DCB=∠ABC=120°
又∵∠1=27°
∴∠BCE=∠DCB -∠1=93°
故答案为93.
【点睛】
本题考查了平行线中关于内错角的性质.解题的关键在于熟练使用两直线平行,内错角相等的性质.
29.①③④
【解析】
根据两直线平行,内错角相等可判断①,根据平行线的性质,折叠性质,利用角的和差判断④,根据平角定义及折叠性质可判断②,根据平角定义可判断③.
解:四边形是长方形,
,,
,
,①正确;
,
,
由折叠得,,,,,
,④正确;
,
,
,
,②错误;
,
,③正确.
故答案为:①③④.
【点睛】
本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.
30.55
【解析】
先根据垂直的定义求出,再由对顶角相等求解即可.
解:∵,
∴,
∴,
∴,
故答案为:55.
【点睛】
本题主要考查了垂直的定义,对顶角相等,熟知相关知识是解题的关键.
31.35°
【解析】
先根据平行线的性质,求出∠DBC=180°-∠D=70°,再根据角平分线的性质得到.
解:∵AD∥BC,
∴∠D+∠DBC=180°,
∵∠D=110°,
∴∠DBC=180°-∠D=70°,
∵BE平分∠DBC,
∴,
故答案为:35°.
【点睛】
本题主要考查了平行线的性质,角平分线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
32.65°
【解析】
根据四边形是长方形,可得,根据平行线的性质可得,,再根据折叠可得,,等量代换后即可得结果.
解:四边形是长方形,
,
,,
根据折叠可知:
,
,
,
,
.
故答案为:.
【点睛】
本题考查了平行线的性质,解决本题的关键是熟练掌握平行线的性质.
33.3
【解析】
根据平行线之间的距离处处相等可得答案.
解:因为△BCD的面积是6平方厘米,BC=4厘米,
所以BC边上的高是:2×6÷4=3(厘米).
故答案为:3.
【点睛】
本题主要考查了平行线间的距离,准确计算是解题的关键.
34.75
【解析】
根据平行线的性质和的度数得到,再利用平角的性质可得的度数.
解:如图:
,,
.
,
.
故答案为:75.
【点睛】
此题考查了平行线的性质,解题的关键是注意掌握两直线平行,同位角相等定理的应用.
35.15°##15度
【解析】
如下图,过点E作EFBC,然后利用平行线的性质结合已知条件进行分析解答即可.
由题意可得ADBC,∠DAE=∠1+45°,∠AEB=90°,∠EBC=30°,过点E作EFBC,
则ADEFBC,
∴∠AEF=∠DAE=∠1+45°,∠FEB=∠EBC=30°,
又∵∠AEF=∠AEB-∠FEB,
∴∠AEF=90°-30°=60°,
∴∠1+45°=60°,
∴∠1=60°-45°=15°.
故答案为:15°.
36.①②③④
【解析】
根据平行线的判定方法:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行进行分析即可.
①∠1=∠2可根据同位角相等,两直线平行得到a∥b;
②∠3=∠6可根据内错角相等,两直线平行得到a∥b;
③若∠1=∠8,则∠2=∠7可根据内错角相等,两直线平行得到a∥b;
④∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b;
故答案为①②③④.
【点睛】
本题考查平行线的判定,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,解题的关键是搞清楚同位角、内错角、同旁内角的概念
37.150°
【解析】
过点B作BE∥AD,
∵AD∥CF,
∴BE∥AD∥CF,
∴∠1=∠A=120°,∠2+∠C=180°,
∵∠ABC=150°,∠1+∠2=∠ABC,
∴∠2=30°,
∴∠C=150°.
38.100°
【解析】
利用对顶角相等即可求得∠AOC的度数,然后根据角平分线的定义求得∠COE的度数,然后根据∠COE和∠EOD互补即可求解.
解:∵∠AOC=∠BOD=40°,
又∵OA平分∠COE,
∴∠COE=2∠AOC=80°,
∴∠EOD=180°-∠COE=180°-80°=100°.
故答案为100°.
【点睛】
本题考查邻补角的定义,对顶角的性质,角平分线的定义,是一个基础题.
39.60°##60度
【解析】
设∠BAF=x°,∠BCF=y°,由题意知∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,如图,过点B作BM∥AD,过点F作FN∥AD,由AD∥CE可得AD∥FN∥BM∥CE,有∠AFN=∠HAF=x°,∠CFN=∠GCF=2y°,ABM=∠BAH=2x°,∠CBM=∠GCB=y°,∠AFC=(x+2y)°,∠ABC=(2x+y)°由于∠F的余角等于2∠B的补角,可知90﹣(x+2y)=180﹣2(2x+y),进行求解可得x的值,进而可求出∠BAH的值.
解:设∠BAF=x°,∠BCF=y°
∵∠BCF=∠BCG,CF与∠BAH的平分线交于点F
∴∠HAF=∠BAF=x°,∠BCG=∠BCF=x°,∠BAH=2x°,∠GCF=2y°,
如图,过点B作BM∥AD,过点F作FN∥AD
∵AD∥CE
∴AD∥FN∥BM∥CE
∴∠AFN=∠HAF=x°,∠CFN=∠GCF=2y°,∠ABM=∠BAH=2x°,∠CBM=∠GCB=y°
∴∠AFC=(x+2y)°,∠ABC=(2x+y)°
∵∠AFC的余角等于2∠ABC的补角
∴90﹣(x+2y)=180﹣2(2x+y)
解得:x=30
∴∠BAH=60°
故答案为:60°.
【点睛】
本题考查了角平分线,平行线的性质,余角、补角等知识.解题的关键在于正确的表示角度之间的数量关系.
40.1
【解析】
连接BD,利用平行线间距离相等得到同底等高的三角形面积相等即可解答.
解:连接BD,如下图所示:
∵BC∥AD,
∴S△AFD= S△ABD,
∴S△AFD- S△AED= S△ABD- S△AED,
即S△AEF= S△BED,
∵AB∥CD,
∴S△BED=S△BEC,
∴S△AEF=S△BEC,
∴S△BCE:S△AEF=1.
故答案为:1.
【点睛】
本题以平行为背景考查了同底等高的三角形面积相等,找到要求的三角形有关的同(等)底或同(等)高是解题的关键.
41.##BC//DE
【解析】
由平分,可得,再根据同旁内角互补两直线平行可得结论.
解:平分,,
∴=2=110°,
,
∴∠C+∠CDE=70°+110°=180°,
.
故答案为:.
【点睛】
本题考查了角的平分线的性质,平行线的判定,熟练的掌握平行线的判定方法是解题关键.
42.100°
【解析】
根据AD//BC可得,∠1=∠ADB,△ABD的内角和为180°,即可求出∠2的度数.
解:∵AD//BC,∴∠1=∠ADB,在△ABD中,∠1+∠2+∠ADB=2∠1+∠2=180°,求出x=10,∠2=(4x+60)°=100°,故答案为100°.
【点睛】
此题考查了平行线的性质和三角形内角和定理,熟练掌握定理是解题的关键.
43.6
【解析】
根据题意利用平行线间距离即所有垂线段的长度相等,可以求得S△ADF=S△ABD,S△ADE=S△ACD,S△CEF=S△BCE,利用面积相等把S△DEF转化为已知△ABC的面积,即可求解.
解:∵BF∥AD∥CE,
∴S△ADF=S△ABD,S△ADE=S△ACD,S△CEF=S△BCE,
∴S△AEF=S△CEF-S△ACE=S△BCE-S△ACE=S△ABC,
S△DEF=S△ADF+S△ADE+S△AEF=S△ABD+S△ACD+S△ABC=S△ABC+S△ABC=2S△ABC=2×3=6,
故答案为:6.
【点睛】
本题考查平行线的推论,注意掌握平行线间距离即所有垂线段的长度相等并利用三角形面积相等,把S△DEF转化为已知△ABC的面积.
44.72
【解析】
本题考查对顶角的定义,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.
解:①两条直线相交共2对对顶角;
②三条直线相交,在2对的基础上再加4对,共6对;
③四条直线相交,在6对的基础上再加6对,共12对;
④五条直线相交,在12对的基础上再加8对,共20对;
即对顶角的对数为,2,6,12,20……,
以此类推,当n条直线相交时,对顶角的总对数为: ;
根据n条直线相交于一点,构成对对顶角的规律可知,
当时,=(92-9)=72(对),
故答案为:72.
【点睛】
本题考查了对顶角的定义及n条直线相交于一点,构成对顶角的规律,注意对顶角是两条直线相交而成的四个角中,没有公共边的两个角.
45.35°或145°
【解析】
分∠1在∠2内部和外部两种情况,画出图形,根据角的和差关系即可得答案.
如图,当∠1在∠2外部时,
∵∠1的两边分别垂直于∠2的两边,
∴∠AOC=∠BOD=90°,
∴∠1+∠BOC=∠2+∠BOC,
∴∠2=∠1=35°.
如图,当∠1在∠2内部时,
∵∠1的两边分别垂直于∠2的两边,
∴∠AOD=∠BOC=90°,
∴∠AOC=∠BOD=90°-∠1=90°-35°=55°,
∴∠2=∠AOC+∠1+∠BOD=55°+35°+55°=145°.
故答案为:35°或145°
【点睛】
本题考查角的运算,分情况正确画出图形是解题关键.
46.40
【解析】
过作平行于,由与平行,得到与平行,利用两直线平行同位角相等,同旁内角互补,得到,,即可确定出的度数.
解:如图:过作平行于,
,
,
,
,即,
.
故答案为:40.
【点睛】
此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.
47.30°
【解析】
根据平行线的性质,可得∠3与∠1的关系,根据两直线垂直,可得所成的角是90°,根据角的和差,可得答案.
解:如图所示:
,
∵直线a∥b,
∴∠3=∠1=60°.
∵AC⊥AB,
∴∠3+∠2=90°,
∴∠2=90°-∠3=90°-60°=30°,
故答案是:30°.
【点睛】
本题考查了平行线的性质,解题的关键是利用了平行线的性质,垂线的性质,角的和差.
48.60
【解析】
根据角平分线的定义、平行线的性质以及平角的定义得到∠BCD=∠BEF,列出方程求解即可.
解:∵AB平分∠FEG,
∴∠AEG=∠AEF,
∵∠AEF=180° ∠BEF,
∴∠AEG=180° ∠BEF,
∵CD∥BG,
∴∠AEG=∠ACD,
∴∠ACD=180° ∠BEF,
∵∠ACD+∠BCD=180°,
∴180° ∠BEF+∠BCD=180°,
∴∠BCD=∠BEF,
∵∠BCD=(100+x)°,∠BEF=(140 x)°,
∴(100+x)°=(140 x)°,
∴100+x=140 x,
∴x=20,
∴∠BCD=(100+20)°=120°,
∴∠ACD=180° ∠BCD=180° 120°=60°,
故答案为:60.
【点睛】
本题考查了平行线与角平分线的性质,解一元一次方程,解题关键是熟练掌握平行线与角平分线的性质.
答案第1页,共2页
同课章节目录
