第13章 相交线、平行线解答题练习(上海地区专用)2021-2022学年下学期上海市各地沪教版七年级数学期中复习 ( word版含解析)
文档属性
| 名称 | 第13章 相交线、平行线解答题练习(上海地区专用)2021-2022学年下学期上海市各地沪教版七年级数学期中复习 ( word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览



文档简介
第13章 相交线 平行线解答题
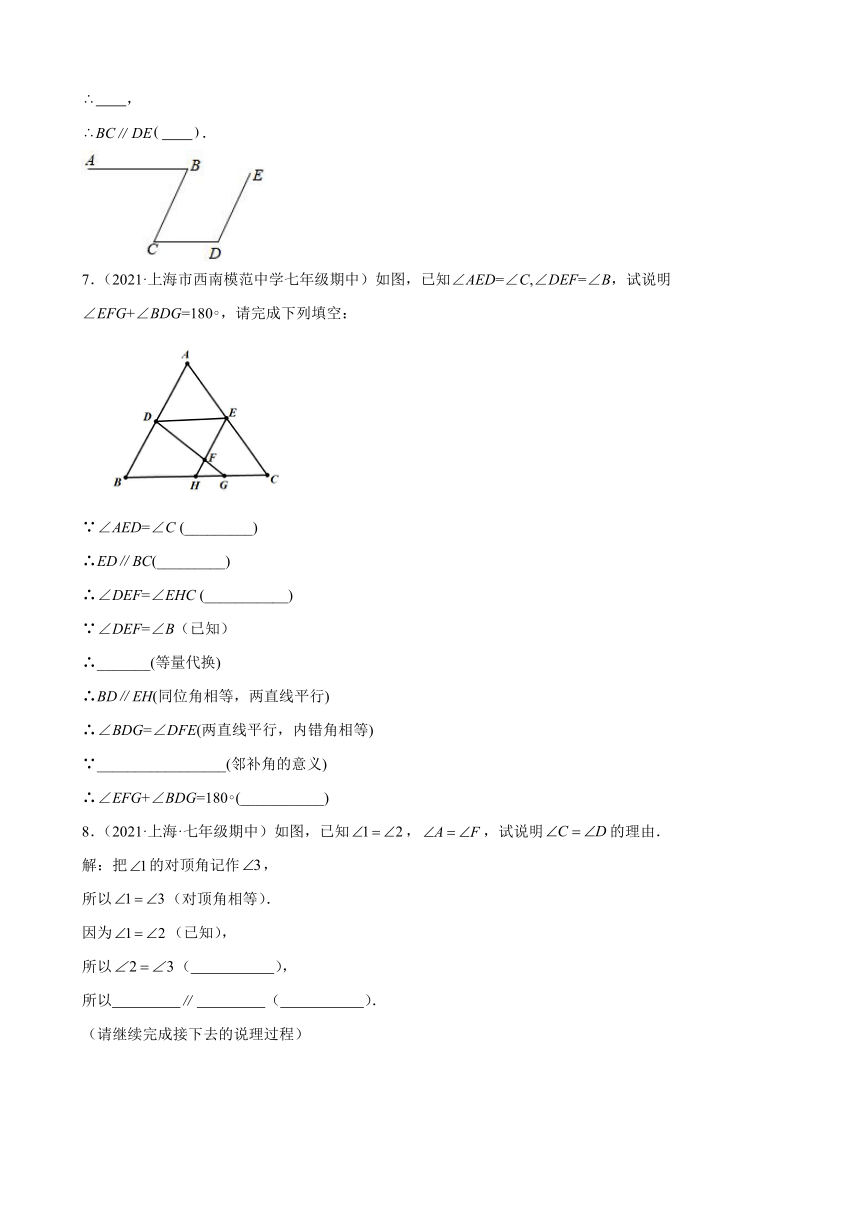
1.(2021·上海市川沙中学南校七年级期中)如图,已知,,平分,求和的度数.
2.(2021·上海市教育学会青浦清河湾中学七年级期中)如图,直线AB、CD被直线EF所截,GH是∠EGC的平分线,∠EGH=56°,∠EIB=68°,说明AB∥CD的理由.
解:因为GH是∠EGC的角平分线( )
所以∠EGH=∠HGC=56°( )
因为CD是条直线(已知)
所以∠HGC+∠EGH+∠IGD=180°( )
所以∠IGD=68°
因为∠EIB=68°(已知)
所以__________=__________( )
所以AB∥CD( )
3.(2021·上海浦东新·七年级期中)如图:∠1+∠2=180°,∠C=∠D,则∠A=∠F吗?请说明理由.
4.(2021·上海·七年级期中)如图,已知于点,于点,,试说明.
解:因为(已知),
所以( ).
同理.
所以( ).
即.
因为(已知),
所以( ).
所以( ).
5.(2021·上海·七年级期中)如图,已知,,是的平分线,,求的度数.
6.(2021·上海市浦东新区新场实验中学七年级期中)如图,ABCD,,,试说明:BCDE.请补充说明过程,并在括号内填上相应的理由.
解:∵ABCD(已知),
,
又(已知),
,
,
,
BCDE .
7.(2021·上海市西南模范中学七年级期中)如图,已知∠AED=∠C,∠DEF=∠B,试说明∠EFG+∠BDG=180 ,请完成下列填空:
∵∠AED=∠C (_________)
∴ED∥BC(_________)
∴∠DEF=∠EHC (___________)
∵∠DEF=∠B(已知)
∴_______(等量代换)
∴BD∥EH(同位角相等,两直线平行)
∴∠BDG=∠DFE(两直线平行,内错角相等)
∵_________________(邻补角的意义)
∴∠EFG+∠BDG=180 (___________)
8.(2021·上海·七年级期中)如图,已知,,试说明的理由.
解:把的对顶角记作,
所以(对顶角相等).
因为(已知),
所以( ),
所以 ( ).
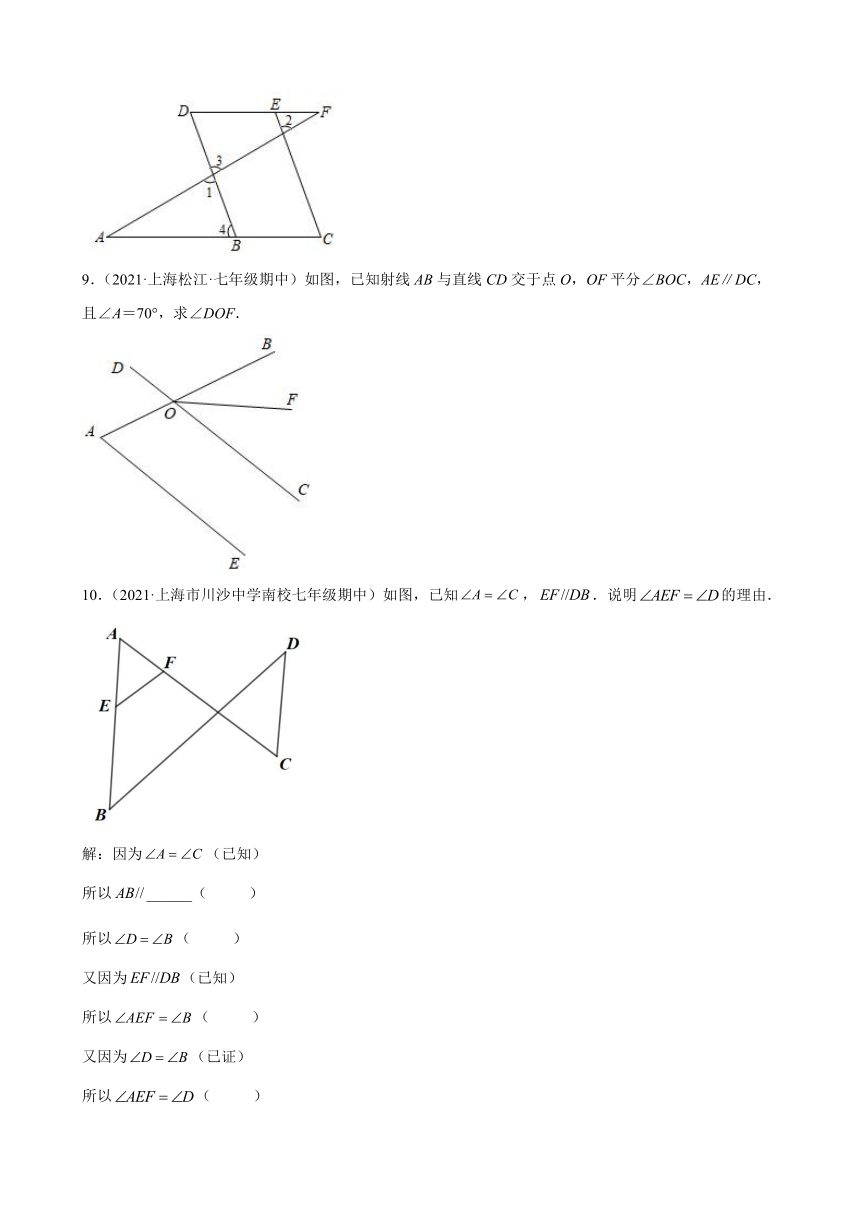
(请继续完成接下去的说理过程)
9.(2021·上海松江·七年级期中)如图,已知射线AB与直线CD交于点O,OF平分∠BOC,AE∥DC,且∠A=70°,求∠DOF.
10.(2021·上海市川沙中学南校七年级期中)如图,已知,.说明的理由.
解:因为(已知)
所以______( )
所以( )
又因为(已知)
所以( )
又因为(已证)
所以( )
11.(2021··七年级期中)如图,直线AE、CF分别被直线EF、AC所截,已知∠1=∠2,AB平分∠EAC,CD平分∠ACG,将下列证明AB//CD的过程及理由填写完整.
证明:因为∠1=∠2,
所以 // ( ),
所以∠EAC=∠ACG( ),
因为AB平分∠EAC,CD平分∠ACG,
所以 =, =,
所以 = ,
所以AB//CD( ).
12.(2021·上海市浦东新区新场实验中学七年级期中)如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.
13.(2021·上海市川沙中学南校七年级期中)按照要求完成下列问题:
如图,直线和相交于点,点为上一点.
(1)过点作的垂线,交于点;
(2)过点作的垂线,交于点;
(3)比较线段和的大小:______.
14.(2021·上海市南洋模范初级中学七年级期中)如图,已知,,,求的度数.
15.(2021·上海市建平实验中学七年级期中)如图,AF、BD、CE是直线,点B在直线AC上,点E在直线DF上.∠A=∠F,∠C=∠D.
说明∠1与∠2互补的理由.
解:因为∠A=∠F(已知),
所以AC∥DF(_______________)
所以__________(_________________)
因为∠C=∠D(已知),
所以∠D=∠4(等量代换),
所以DB∥CE(______________________),
所以∠2+∠3=180°(_________________),
因为∠1=∠3(__________________),
所以∠2+∠1=180°(等量代换).
16.(2021·上海市第二初级中学七年级期中)如图,已知,点在的上方,则、、之间存在怎样的等量关系?说明理由.
解:过点做,
______(两直线平行,内错角相等),
(已知),
(已作),
____________(______).
17.(2021·上海市南洋模范初级中学七年级期中)如图,已知,,于点,那么与有什么数量关系?为什么?
18.(2021·上海杨浦·七年级期中)如图,已知AB∥CD,直线MN分别交直线AB、CD于点E、F,射线EG、FH分别平分∠AEF、∠DFE,试说明EG∥FH的理由.
解:因为AB∥CD(已知),
所以∠AEF=∠DFE( ),
因为射线EG、FH分别平分∠AEF、∠DFE(已知),
所以∠ =∠AEF,
∠ =∠EFD ( ).
所以 (等式性质).
所以EG∥FH( ).
19.(2021·上海杨浦·七年级期中)如图:∠1=∠2,∠D=90°,EF⊥CD,试说明∠3=∠B.
20.(2021·上海杨浦·七年级期中)如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB ( ),
所以∠1+ =180° ( ).
因为∠1=∠A(已知),
所以∠A+ =180° ( ).
所以DE∥AC ( ).
21.(2021··七年级期中)如图,已知直线AB//EF,AB//CD,∠ABE=50°,EC平分∠BEF,求∠DCE的度数.
22.(2021·上海·七年级期中)(1)探究:如图1,ABCDEF,试说明.
(2)应用:如图2,ABCD,点在、之间,与交于点,与交于点.若,,则的大小是多少?
(3)拓展:如图3,直线在直线、之间,且ABCDEF,点、分别在直线、上,点是直线上的一个动点,且不在直线上,连接、.若,则 度(请直接写出答案).
23.(2021·上海市罗南中学七年级期中)如图1,已知AB∥CD,直线AB、CD把平面分成①、②、③三个区域(直线AB、CD不属于①、②、③中任何一个区域).点P是直线AB、CD、AC外一点,联结PA、PC,可得∠PAB、∠PCD、∠APC.
(1)如图2,当点P位于第①区域一位置时,请填写∠APC=∠PAB+∠PCD的理由.
解:过点P作PE//AB,
因为AB//CD,PE//AB,
所以PE//CD( ).
因为PE//AB,
所以∠APE=∠PAB( ).
同理∠CPE=∠PCD.
因此∠APE+∠CPE=∠PAB+∠PCD.
即∠APC=∠PAB+∠PCD.
(2)在第(1)小题中改变点P的位置,如图3所示,求∠APC+∠PAB+∠PCD等于多少度?为什么?
(3)当点P在第②区域时,∠PAB、∠PCD、∠APC有怎样的数量关系?请画出图形,并直接写出相应的结论.
24.(2021·上海市南洋模范初级中学七年级期中)如图,AB、CD是两条直线,,.请说明的理由.
25.(2021·上海市教育学会青浦清河湾中学七年级期中)已知,直线AB∥CD
(1)如图(1),点G为AB、CD间的一点,联结AG、CG.若∠A=140°,∠C=150°,则∠AGC的度数是多少?
(2)如图(2),点G为AB、CD间的一点,联结AG、CG.∠A=x°,∠C=y°,则∠AGC的度数是多少?
(3)如图(3),写出∠BAE、∠AEF、∠EFG、∠FGC、∠GCD之间有何关系?直接写出结论.
26.(2021·上海市建平实验中学七年级期中)如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求三角形CAD的面积.
27.(2021·上海市罗南中学七年级期中)如图,已知∠ADC=∠ABC,DE、BF分别平分∠ADC和∠ABC,且DE∥BF,那么AB与DC平行吗?为什么?
28.(2021·上海松江·七年级期中)如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
解:因为AD⊥BC,EF⊥BC(______ )
所以∠ADC=90°,∠EFD=90°(______ )
得∠ADC=∠EFD(等量代换),
所以AD∥EF(______ )
得∠2+∠3=180°(______ )
由∠1+∠2=180°(______ )
得∠1=∠3(______ )
所以DG∥AB(______ )
所以∠CGD=∠CAB(______ )
29.(2021·上海·七年级期中)已知,点为平面内的一点,.
(1)当点在如图①的位置时,求与的数量关系.
解: .(根据如图填射线的画法)
因为,
所以 ( ).
所以(两直线平行,内错角相等);
(请继续完成接下去的说理过程)
(2)当点在如图②的位置时,与的数量关系是 (直接写出答案);
(3)在(2)的条件下,如图③,过点作,垂足为点,与的平分线分别交射线于点、,回答下列问题(直接写出答案):图中与相等的角是 , 度.
30.(2021·上海市民办文绮中学七年级期中)如图,D,E,G分别是AB,AC,BC边上的点,,.
(1)请说明的理由;
(2)若DE平分,,判断CD与EG的位置关系,并说明理由.
31.(2021··七年级期中)如图,已知,且,试说明的理由.
32.(2021·上海市第二初级中学七年级期中)如图所示,已知平分,,那么与相等吗?完成下面的填空.
平分(已知)
______(______),
(已知),
______(______),
____________(______),
(______).
33.(2021·上海市浦东新区新场实验中学七年级期中)请回答下列各题.
(1)探究:如图1,AB∥CD∥EF,试说明∠BCF=∠B+∠F.
(2)应用:如图2,AB∥CD,点F在AB、CD之间,FE与AB交于点M,FG与CD交于点N.若∠EFG=115°,∠EMB=55°,则∠DNG的大小是多少?
(3)拓展:如图3,直线CD在直线AB、EF之间,且AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连结QG、QH.若∠GQH=70°,则∠AGQ+∠EHQ=______度(请直接写出答案).
34.(2021·上海市建平实验中学七年级期中)(1)如图示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系; ②请说明理由.
35.(2021·上海杨浦·七年级期中)已知:AB∥CD,截线MN分别交AB、CD于点M、N.
(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足+(β﹣60)2=0,求∠BEM的度数;
(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;
(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为 (直接写出答案).
36.(2021·上海市民办文绮中学七年级期中)已知,点B为平面内一点,于B.
(1)如图,直接写出和之间的数量关系.
(2)如图,过点B作于点D,求证:.
(3)如图,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF那平分,BE平分,若,,求的度数.
37.(2021·上海市南洋模范初级中学七年级期中)(1)如图1,已知直线,在直线上取两点,为直线上的两点,无论点移动到任何位置都有:____________(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形,中间有条分界小路(图中折线),左边区域为王爷爷的,右边区域为李爷爷的。现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由。(不计分界小路与直路的占地面积).
38.(2021··七年级期中)问题情境:如图1,ABCD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:如图2,过P作PEAB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 度;
(2)如图3,ADBC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
试卷第1页,共3页
参考答案:
1.,
【解析】
根据两直线平行,同位角相等求出∠EAD=∠B,再根据角平分线的定义可得∠DAC=∠EAD,然后利用两直线平行,内错角相等可得∠C=∠DAC.
∵(已知)
∴(两直线平行,同位角相等)
∵(已知)
∴(等量代换)
∵平分(已知)
∴(角平分线的意义)
∵(已知)
∴(两直线平行,内错角相等)
∴(等量代换)
∵(已证)
∴(等量代换)
【点睛】
本题主要考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.
2.角平分线的意义,平角的意义,∠IGD,∠EIB,等量代换,同位角相等,两直线平行
【解析】
根据题意和图形,可以写出解答过程中空格中需要填写的内容,本题得以解决.
解:因为GH是∠EGC的角平分线( 已知 )
所以∠EGH=∠HGC=56°(角平分线的意义)
因为CD是条直线
所以∠HGC+∠EGH+∠IGD=180°(平角的意义)
所以∠IGD=68°
因为∠EIB=68°
所以__∠IGD __=__∠EIB __(等量代换)
所以AB∥CD(同位角相等,两直线平行)
【点睛】
本题考查平行线的判定,解答本题的关键是明确题意,利用数形结合的思想解答.
3.∠A=∠F,理由见解析
【解析】
∠1+∠2=180°,∠2=∠AGC,∠1+∠AGC=180°,BD∥CE,有∠C=∠ABD=∠D,得DF∥AC,进而可说明∠A=∠F.
解:∠A=∠F,理由如下:
∵∠1+∠2=180°,∠2=∠AGC
∴∠1+∠AGC=180°
∴BD∥CE
∴∠C=∠ABD
∵∠C=∠D
∴∠D=∠ABD
∴DF∥AC
∴∠A=∠F.
【点睛】
本题考查了对顶角,平行线的判定与性质.解题的关键在利用角的数量关系证明直线平行.
4.垂直的定义;等量代换;等式的性质1;内错角相等,两直线平行
【解析】
根据垂直定义得出,求出,根据平行线的判定推出即可.
解:因为(已知),
所以(垂直的定义),
同理.
所以(等量代换),
即.
因为(已知),
所以(等式的性质,
所以(内错角相等,两直线平行).
故答案为:垂直的定义;等量代换;等式的性质1;内错角相等,两直线平行
【点睛】
本题考查了垂直定义和平行线的判定的应用,熟练掌握平行线的判定是解题关键.
5.
【解析】
根据平行线的性质求出∠BCE的度数,根据角平分线的性质求出∠BCN的度数,然后根据垂直的定义求出.
解:∵ ,,
∴,
∵是的平分线,
∴,
∵,
∴.
【点睛】
本题主要考查了平行线的性质、角平分线的定义和垂直的定义,熟知两直线平行,同位角相等,内错角相等,同旁内角互补是解题关键.
6.两直线平行,内错角相等;55;等量代换;已知;;同旁内角互补,两直线平行
【解析】
由题意根据平行线的性质与判定即可补充说理过程.
解:(已知),
(两直线平行,内错角相等),
又(已知),
(等量代换),
(已知),
,
(同旁内角互补,两直线平行).
故答案为:两直线平行,内错角相等;55;等量代换;已知;;同旁内角互补,两直线平行.
【点睛】
本题考查平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
7.已知;同位角相等,两直线平行;两直线平行,内错角相等;∠EHC =∠B;∠DFE+∠EFG =180 ;等量代换
【解析】
根据同位角相等,两直线平行推出ED∥BC,通过两直线平行,内错角相等推出∠DEF=∠EHC,再运用等量代换得到∠EHC =∠B,最后推出BD∥EH,∠BDG=∠DFE,再利用邻补角的意义推出结论,据此回答问题.
解:∵∠AED=∠C (已知)
∴ED∥BC(同位角相等,两直线平行)
∴∠DEF=∠EHC (两直线平行,内错角相等)
∵∠DEF=∠B(已知)
∴∠EHC =∠B (等量代换)
∴BD∥EH(同位角相等,两直线平行)
∴∠BDG=∠DFE(两直线平行,内错角相等)
∵∠DFE+∠EFG =180 (邻补角的意义)
∴∠EFG+∠BDG=180 (等量代换).
【点睛】
本题主要考查平行线的判定和性质,属于综合题,难度一般,熟练掌握平行线的判定和性质是解题关键.
8.等量代换;BD;CE;同位角相等,两直线平行;见解析
【解析】
根据平行线的判定与性质求解即可.
解:把的对顶角记作,
所以(对顶角相等).
因为(已知),
所以(等量代换),
所以(同位角相等,两直线平行),
所以(两直线平行,同位角相等),
又因为,
所以(同位角相等,两直线平行),
所以(两直线平行,内错角相等),
所以(等量代换).
故答案为:等量代换;;;同位角相等,两直线平行.
【点睛】
本题主要考查了平行线的性质与判定的综合应用,熟练掌握平行线的性质与判定方法是解答本题的关键.解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
9.145°
【解析】
根据平行线的性质,两直线平行,同位角相等可得∠A=∠BOC=70°,由角平分线的性质可得∠BOF=∠FOC=35°,再根据平角的性质即可得出答案.
解:∵AE∥DC,
∴∠A=∠BOC=70°,
又∵OF平分∠BOC,
∴∠BOF=∠FOC=35°,
∴∠DOF=180°-∠FOC=180°-35°=145°.
【点睛】
本题主要考查了平行线的性质、邻补角的概念等,熟练应用平行线的性质进行求解是解决本题的关键.
10.CD;内错角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;等量代换
【解析】
根据平行线的判定与性质解答即可.
解:因为(已知),
所以CD(内错角相等,两直线平行),
所以(两直线平行,内错角相等),
又因为(已知),
所以(两直线平行,同位角相等),
又因为(已证),
所以(等量代换),
故答案为:CD;内错角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;等量代换.
【点睛】
本题考查平行线的判定与性质,熟练掌握平行线的判定与性质,能正确写出每一步结论的依据是解答的关键.
11.AE;FG;同位角相等,两直线平行;两直线平行,内错角相等;∠3;∠4;∠3;∠4;内错角相等,两直线平行
【解析】
利用平行线的判定及性质就可求得本题.即同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.反之即为性质.
证明:因为∠1=∠2,
所以AE∥CF(同位角相等,两直线平行),
所以∠EAC=∠ACG(两直线平行,内错角相等),
因为AB平分∠EAC,CD平分∠ACG,
所以∠3=∠EAC,∠4=∠ACG,
所以∠3=∠4,
所以AB∥CD(内错角相等,两直线平行).
故答案为:AE;FG;同位角相等,两直线平行;两直线平行,内错角相等;∠3;∠4;∠3;∠4;内错角相等,两直线平行.
【点睛】
本题主要考查了平行线的判定和性质.正确的识别图形是解题的关键.
12.证明见解析.
【解析】
根据平行线的判定与性质即可证明.
∵AD⊥BC,EF⊥BC,
∴AD∥EF,∴∠1+∠2=180°,
∵∠2+∠3=180°,∴∠1=∠3
∴AB∥DG,
∴∠GDC=∠B.
【点睛】
此题主要考查平行线的性质与判定,解题的关键是熟知平行线的判定.
13.(1)作图见详解;(2)作图见详解;(3).
【解析】
(1)、(2)利用题中几何语言画出对应的几何图形即可;
(3)根据垂线段最短求解即可.
解:(1)如图,为所作;
(2)如图,为所作;
(3)利用垂线段最短可判断.
【点睛】
本题考查了作图-基本作图,垂线段最短的性质,熟悉相关性质是解题的关键.
14.
【解析】
利用“两直线平行,同旁内角互补”列方程求解即可.
解:,,
即得,解得.
【点睛】
本题考查了平行线的性质,掌握“两直线平行,同旁内角互补”的性质是解题关键.
15.内错角相等,两直线平行;∠4=∠C;两直线平行,内错角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;对顶角相等
【解析】
由∠A=∠F ,可得AC∥DF,从而∠4=∠C,又由∠C=∠D,可得∠D=∠4,得到DB∥CE ,从而∠2+∠3=180°,再由对顶角相等,即可求解.
解:因为∠A=∠F(已知),
所以AC∥DF( 内错角相等,两直线平行 )
所以∠4=∠C( 两直线平行,内错角相等 )
因为∠C=∠D(已知),
所以∠D=∠4(等量代换),
所以DB∥CE( 同位角相等,两直线平行 ),
所以∠2+∠3=180°( 两直线平行,同旁内角互补 ),
因为∠1=∠3( 对顶角相等 ),
所以∠2+∠1=180°(等量代换).
【点睛】
本题主要考查了平行线的判定和性质,对顶角的定义,熟练掌握平行线的判定和性质是解题的关键.
16.,理由见解析;,,,平行于同一条直线的两条直线平行
【解析】
根据平行线的性质得,根据平行于同一条直线的两条直线平行得,根据平行线的性质得,根据角之间的关系等量代换即可得.
解:过点E作,
∴(两直线平行,内错角相等),
∴(已知),
(已知),
∴(平行于同一条直线的两条直线平行),
∴,
∵,
∴.
【点睛】
本题考查了平行线的性质,解题的关键是掌握平行线的性质.
17.∠4与∠5互余,理由见解析
【解析】
由题意知∠2+∠3=90°,∠1+∠4=90°,∠2+∠4=90°,∠2=∠5,得到∠5+∠4=90°,进而可判断两角关系.
解:∠4与∠5互余,
理由:∵OE⊥OA,
∴∠AOE=90°,即∠2+∠3=90°,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠4=90°
∵∠1=∠2,
∴∠2+∠4=90°,
∵,∴∠2=∠5,
∴∠5+∠4=90°,即∠4与∠5互余.
【点睛】
本题考查了同角的余角相等,平行线的性质.解题的关键在于找出角度的数量关系.
18.两直线平行内错角相等;GEF;EFH;角平分线的定义;∠GEF=∠EFH;内错角相等两直线平行.
【解析】
根据平行线的性质、角平分线的定义及平行线的判定逐一求解即可.
解:因为AB∥CD(已知),
所以∠AEF=∠DFE(两直线平行内错角相等),
因为射线EG、FH分别平分∠AEF、∠DFE(已知),
所以∠GEF=∠AEF,
∠EFH=∠EFD (角平分线的定义).
所以∠GEF=∠EFH(等式性质).
所以EG∥FH(内错角相等两直线平行).
故答案为:两直线平行内错角相等;GEF;EFH;角平分线的定义;∠GEF=∠EFH;内错角相等两直线平行.
【点睛】
本题主要考查了平行线的判定与性质,准确判断是解题的关键.
19.见解析
【解析】
因为∠1=∠2,由内错角相等证明AD∥BC,又因为∠D=90°,EF⊥CD,则有AD∥EF,所以EF∥BC,故可求证∠3=∠B.
解:∵∠1=∠2,
∴AD∥BC,
∵∠D=90°,
∴AD⊥CD,
∵EF⊥CD,
∴AD∥EF,
∴EF∥BC,
∴∠3=∠B.
【点睛】
本题主要考查了平行线的判定与性质,准确计算是解题的关键.
20.已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行
【解析】
根据平行线的判定、等量代换及平行线的判定逐一求解即可.
解:因为DF∥AB (已知),
所以∠1+∠DEA=180° (两直线平行同旁内角互补).
因为∠1=∠A(已知),
所以∠A+∠DEA=180° (等量代换).
所以DE∥AC (同旁内角互补两直线平行).
故答案为:已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行.
【点睛】
本题主要考查了平行线的判定与性质,准确判断是解题的关键.
21.∠DCE=155°
【解析】
利用平行线的性质、平行公理及角平分线的定义即可求解.
解:∵AB//EF,∠ABE=50°(已知)
∴∠ABE=∠BEF=50°(两直线平行,内错角相等)
∵EC平分∠BEF(已知)
∴∠CEF=∠BEF=25°(角平分线的意义)
∵AB//EF,AB//CD(已知)
∴CD//EF(平行线的传递性)
∴∠CEF+∠DCE=180°(两直线平行,同旁内角互补)
∴∠DCE=180°-25°=155°(等式性质).
【点睛】
本题考查了平行线的性质、平行公理及角平分线的定义,熟练掌握有关定理、定义是解题的基础.
22.(1)见解析;(2)60°;(3)70或290
【解析】
(1)由可得,,,则;
(2)利用(1)中的结论可知,,则可得的度数为,由对顶角相等可得;
(3)结合(1)中的结论可得,注意需要讨论是钝角或是锐角时两种情况.
解:(1)如图1,,
,,
,
.
(2)由(1)中探究可知,,
,且,
,
;
(3)如图,当为钝角时,
由(1)中结论可知,,
;
当为锐角时,如图,
由(1)中结论可知,,
即,
综上,或.
故答案为:70或290.
【点睛】
本题主要考查平行线的性质与判定,难度适中,观察图形,推出角之间的和差关系是解题关键.
23.(1)平行的传递性;两直线平行,内错角相等;
(2)360°,理由见解析;
(3)∠PCD =∠PAB+∠APC,见解析.
【解析】
(1)根据平行线的性质解题;
(2)过点P作PE//AB,由两直线平行,同旁内角相等解得∠APE+∠PAB=180°,∠EPC+∠PCD=180°,再根据∠APC+∠PAB+∠PCD=∠APE+∠EPC+∠PAB+∠PCD解题;
(3)根据题意,画出图形,再由两直线平行,内错角相等得到∠APE=∠PAB,∠PCD=∠CPE,结合∠CPE=∠APE+∠APC解题.
(1)
解:因为AB//CD,PE//AB,
所以PE//CD(平行的传递性)
因为PE//AB,
所以∠APE=∠PAB(两直线平行,内错角相等).
故答案为:平行的传递性;两直线平行,内错角相等;
(2)
∠APC+∠PAB+∠PCD=360°,
见解析:
过点P作PE//AB,
所以∠APE+∠PAB=180°,
因为PE//CD,
所以∠EPC+∠PCD=180°,
所以∠APC+∠PAB+∠PCD=∠APE+∠EPC+∠PAB+∠PCD=180°+180°=360°;
(3)
∠PCD =∠PAB+∠APC,理由如下,
当点P在第②区域时,如图,
过点P作PE//AB,
所以∠APE=∠PAB,
因为PE//CD,
所以∠PCD=∠CPE
因为∠CPE=∠APE+∠APC
所以∠PCD =∠PAB+∠APC.
【点睛】
本题考查平行线的拐角问题、平行线的性质等知识,是重要考点,掌握相关知识是解题关键.
24.见解析
【解析】
根据平行线的判定得出AB∥CD,根据平行线的性质得出∠AMN=∠MND,求出∠EMN=∠MNF,根据平行线的判定得出ME∥NF,根据平行线的性质得出即可.
∵∠BMN=∠CNM(已知),
∴(内错角相等,两直线平行).
∴∠AMN=∠MND(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠EMN=∠MNF(等式性质).
∴(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等),
【点睛】
本题考查了平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.
25.(1)70°;(2)∠AGC=(x+y)°;(3)∠BAE+∠EFG+∠GCD=∠AEF+∠FGC.
【解析】
(1)过点G作GE∥AB,利用平行线的性质即可进行转化求解.
(2)过点G作GF∥AB,利用平行线的性质即可进行转化求解.
(3)过点E作EM∥AB,过点F作FN∥AB,过点G作GQ∥CD,利用平行线的性质即可进行转化找到角的关系.
解:(1)如图,过点G作GE∥AB,
∵AB∥GE,
∴∠A+∠AGE=180°(两直线平行,同旁内角互补).
∵∠A=140°,
∴∠AGE=40°.
∵AB∥GE,AB∥CD,
∴GE∥CD.
∴∠C+∠CGE=180°(两直线平行,同旁内角互补).
∵∠C=150°,
∴∠CGE=30°.
∴∠AGC=∠AGE+∠CGE=40°+30°=70°.
(2)如图,过点G作GF∥AB
∵AB∥GF,
∴∠A=AGF(两直线平行,内错角相等).
∵AB∥GF,AB∥CD,
∴GF∥CD.
∴∠C=∠CGF.
∴∠AGC=∠AGF+∠CGF=∠A+∠C .
∵∠A=x°,∠C=y°,
∴∠AGC=(x+y)°.
(3)如图所示,过点E作EM∥AB,过点F作FN∥AB,过点G作GQ∥CD,
∵AB∥CD,
∴AB∥EM∥FN∥GQ∥CD.
∴∠BAE=∠AEM,∠MEF=∠EFN,∠NFG=∠FGQ,∠QGC=∠GCD(两直线平行,内错角相等).
∴∠AEF=∠BAE+∠EFN,∠FGC=∠NFG+GCD.
∵∠EFN+∠NFG=∠EFG,
∴∠BAE+∠EFG+∠GCD=∠AEF+∠FGC.
【点睛】
本题考查平行线的判定与性质,本题构造辅助线利用平行线的传递性结合平行线性质是解题关键.
26.6
【解析】
结合题意,根据平行线的性质,得ADBC;AD到BC的距离设为a,根据三角形面积公式和代数式的性质,得,从而完成求解.
∵∠1=∠2
∴ ADBC(内错角相等,两直线平行),
AD到BC的距离设为a,
∴三角形ABC面积==3,
∴
∵AD=2BC
∴三角形ACD面积==6.
【点睛】
本题考查了平行线、代数式的知识;结果的关键是熟练掌握平行线、代数式的性质,从而完成求解.
27.AB∥DC,理由见解析.
【解析】
根据平行线的性质推出∠DEA=∠FBA,再根据角平分线性质推出∠CDE=∠FBA,等量代换得到∠CDE=∠DEA,根据平行线的判定推出即可.
解:AB∥DC,理由如下:
∵DE∥BF,
∴∠DEA=∠FBA,
∵∠ADC=∠ABC,DE、BF分别平分∠ADC和∠ABC,
∴∠CDE=∠CDA=∠CBA=∠FBA=∠DEA,
∴AB∥DC.
【点睛】
本题主要考查对平行线的性质和判定,角平分线性质等知识点的理解和掌握,能推出∠CDE=∠DEA是解此题的关键.
28.已知 垂直定义 同位角相等,两直线平行 两直线平行,同旁内角互补 已知 同角的补角相等 内错角相等,两直线平行 两直线平行,同位角相等
【解析】
求出AD∥EF,根据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
【点睛】
本题考查了平行线的性质和判定,垂直定义,补角的性质,能综合运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之即为平行线的判定.
29.(1)过点作;;;;如果一条直线和两条平行线中的一条平行,那么它和另一条也平行;见解析
(2)
(3),45
【解析】
(1)过点作,先根据平行线的判定与性质可得,,再根据角的和差、等量代换即可得出结论;
(2)过点作,先根据平行线的判定与性质可得,,再根据、角的和差即可得出结论;
(3)过点作,先根据平行线的判定与性质可得,从而可得,再结合(2)的结论可得,然后根据角平分线的定义可得,最后根据即可得出答案
(1)
解:如图①,过点作,
,
(如果一条直线和两条平行线中的一条平行,那么它和另一条也平行).
.
,
.
.
,
.
.
(2)
解:如图②,过点作,
.
,
.
.
,
.
.
.
故答案为:.
(3)
解:如图③,过点作,
,
,
.
,
,
.
.
,
由(2)已得:,
;
平分,
.
平分,
.
,
故答案为:,45.
【点睛】
本题考查了平行线的判定与性质,角平分线的定义等知识点,通过作辅助线,构造平行线是解题关键.
30.(1)证明见解析;
(2),证明见解析.
【解析】
(1)根据已知条件和对顶角相等可证明ABEG,再根据平行线的性质得角相等,再等量代换可得∠3=∠EGC,进而可得DE BC;
(2)根据已知条件可得∠B=45°,可以证明CD⊥AB,再由ABEG,即可得CD⊥EG.
(1)
解:∵,,
∴,
∴,
∴.
又∵,
∴,
∴;
(2)
∵DE平分,
∴.
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,
∴.
【点睛】
本题考查了平行线的判定与性质,解决本题的关键是区别平行线的判定与性质并熟练运用.
31.详见解析
【解析】
由CD∥AB,可得,由,由等量代换可得,即可完成证明.
证明:∵(已知)
∴(两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行)
【点睛】
本题考查了平行线的性质和判定,解题的关键是通过图形分析证明思路.
32.3;角平分线的定义;3;等量代换;内错角相等,两直线平行;两直线平行,同位角相等
【解析】
根据题目给定的思路分析题意,利用平行线的判定和性质进行证明,并填写证明依据即可.
平分(已知)
(角平分线的定义),
(已知),
(等量代换),
(内错角相等,两直线平行),
(两直线平行,同位角相等).
【点睛】
本题主要考查了平行线的判定和性质,解题的关键是区分其关系.
33.(1)证明见解析
(2)60°
(3)70或290
【解析】
(1)由 可得,∠B=∠BCD,∠F=∠DCF,从而可以证明结论成立;
(2)由∠MFN=∠AMF+∠CNF,则可得∠CNF的度数为60°,由对顶角相等可得;
(3)分两种情况讨论,即∠AGQ是钝角与∠AGQ是锐角时.
(1)
证明:∵AB∥CD,
∴∠B=∠BCD.(两直线平行内错角相等),
同理可证,∠F=∠DCF.
∵∠BCF=∠BCD+∠DCF,
∴∠BCF=∠B+∠F.(等量代换)
(2)
解:由探究可知:∠MFN=∠AMF+∠CNF,∠MFN=115°,,
∴∠CNF=∠DNG=115°-55°=60°.
故答案为:60°.
(3)
如图3中,当点Q在直线GH的右侧时,
∵AB∥CD∥EF,
∴∠AGQ+∠GQC=180°,∠CQH+∠EHQ=180°,
即∠AGQ+∠GQH+∠EHQ=180°,
∴∠AGQ+∠EHQ=360°-70°=290°,
当点Q在直线GH的左侧时,由(1)的结论可得:
.
故答案为:70或290.
【点睛】
本题主要考查平行线的性质与判定,熟练运用平行线的性质是解题关键.
34.(1)证明见解析;(2)∠1+∠2-∠E=180°.
【解析】
(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1,由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
解:(1)过点E作EF∥AB,
∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),
∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),
∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),
∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.
【点睛】
本题考查了平行线的性质,作辅助线并熟记性质是解题的关键.
35.(1)30°;(2)∠DEF+2∠CDF=150°,理由见解析;(3)
【解析】
(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;
(2)过点E作直线EH∥AB,由角平分线的性质和平行线的性质可求∠DEF=180°﹣30°﹣2x°=150°﹣2x°,由角的数量可求解;
(3)由平行线的性质和外角性质可求∠PMB=2∠Q+∠PCD,∠CPM=2∠Q,即可求解.
解:(1)∵+(β﹣60)2=0,
∴α=30,β=60,
∵AB∥CD,
∴∠AMN=∠MND=60°,
∵∠AMN=∠B+∠BEM=60°,
∴∠BEM=60°﹣30°=30°;
(2)∠DEF+2∠CDF=150°.
理由如下:过点E作直线EH∥AB,
∵DF平分∠CDE,
∴设∠CDF=∠EDF=x°;
∵EH∥AB,
∴∠DEH=∠EDC=2x°,
∴∠DEF=180°﹣30°﹣2x°=150°﹣2x°;
∴∠DEF=150°﹣2∠CDF,
即∠DEF+2∠CDF=150°;
(3)如图3,设MQ与CD交于点E,
∵MQ平分∠BMT,QC平分∠DCP,
∴∠BMT=2∠PMQ,∠DCP=2∠DCQ,
∵AB∥CD,
∴∠BME=∠MEC,∠BMP=∠PND,
∵∠MEC=∠Q+∠DCQ,
∴2∠MEC=2∠Q+2∠DCQ,
∴∠PMB=2∠Q+∠PCD,
∵∠PND=∠PCD+∠CPM=∠PMB,
∴∠CPM=2∠Q,
∴∠Q与∠CPM的比值为,
故答案为:.
【点睛】
本题主要考查了平行线的性质、角平分线的性质,准确计算是解题的关键.
36.(1)
(2)证明见解析
(3)
【解析】
(1)根据平行线的性质及直角三角形的性质证明即可;
(2)过点B作,根据同角的余角相等得出,再根据平行线的性质得到,即可得到;
(3)过点B作,根据角平分线的定义得出,设,,可得,再根据,得到,解方程得到,继而得出,.
(1)
如图1,
∵,
∴,
∵,
∴,
∴,,
故答案为:;
(2)
如图2,过点B作,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,.
(3)
如图3,过点B作,
∵BF平分,BE平分,
∴,,
由(2)知,
∴,设,,
则,,,
,
∴
∵,,
∴,
中,由得
,
∵,
∴,
∴,
∴,
∴.
【点睛】
本题考查平行线的性质与应用、角平分线的性质、方程思想等知识,学会添加辅助线,掌握相关知识是解题关键.
37.(1);(2)见解析;(3)见解析
【解析】
(1)根据平行线间的距离处处相等,所以无论点在m上移动到何位置,总有与同底等高,因此它们的面积相等;
(2)利用同底等高的三角形的面积相等即可求得设计方案;
(3)连结,过点作的平行线,连结或,则或即为所修直路.
(1)∵与有共同的边AB,
又∵,
∴与的高相等,即与同底等高,
∴=,
故答案为:=;
(2)方法一:
连结,将的区域用于种植大豆,的区域用于种植芝麻,理由如下:
在梯形ABCD中,,
则与同底等高,
∴,
∴,
即,
又由可知与同底等高,
∴,
∴该设计方案把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变;
方法二
连结,将的区域用于种植大豆,的区域用于种植芝麻,理由如下:
在梯形ABCD中,,
则与同底等高,
∴,
∴,
即,
又由可知与同底等高,
∴,
∴该设计方案把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变;
(3)方法一
连结,过点作的平行线:连结,即为所修直路.
将四边形的区域分给王爷爷,四边形的区域分给李爷爷,理由如下:
∵,则与同底等高,
∴,则,
即,
又由可知与同底等高,
∴,
∴满足修路方案;
方法二:
连结,过点作的平行线:连结,即为所修直路.
将四边形的区域分给王爷爷,四边形的区域分给李爷爷,理由如下:
∵,则与同底等高,
∴,则,
即,
又由可知与同底等高,
∴,
∴满足修路方案.
【点睛】
本题主要考查了两条平行线间的距离处处相等.只要两个三角形是同底等高的,则两个三角形的面积一定相等.解题的关键还要根据等式的性质进一步进行变形.
38.(1)110°;(2)∠CPD=∠α+∠β,见解析;(3)当P在BA延长线时,∠CPD=∠β-∠α;当P在AB延长线上时,∠CPD=∠α-∠β
【解析】
(1)过P作PEAB,通过平行线性质求∠APC即可;
(2)过P作PEAD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(3)画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
解:(1)过点P作PEAB,
∵ABCD,
∴PEABCD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°;
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵ADBC,
∴ADPEBC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,∠CPD=∠β-∠α,
理由是:如图4,过P作PEAD交CD于E,
∵ADBC,
∴ADPEBC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE-∠DPE =∠β-∠α;
当P在AB延长线时,∠CPD=∠α-∠β,
理由是:如图5,过P作PEAD交CD于E,
∵ADBC,
∴ADPEBC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE -∠CPE =∠α-∠β.
【点睛】
本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较典型的题目,分类讨论是解题的关键.
答案第1页,共2页
1.(2021·上海市川沙中学南校七年级期中)如图,已知,,平分,求和的度数.
2.(2021·上海市教育学会青浦清河湾中学七年级期中)如图,直线AB、CD被直线EF所截,GH是∠EGC的平分线,∠EGH=56°,∠EIB=68°,说明AB∥CD的理由.
解:因为GH是∠EGC的角平分线( )
所以∠EGH=∠HGC=56°( )
因为CD是条直线(已知)
所以∠HGC+∠EGH+∠IGD=180°( )
所以∠IGD=68°
因为∠EIB=68°(已知)
所以__________=__________( )
所以AB∥CD( )
3.(2021·上海浦东新·七年级期中)如图:∠1+∠2=180°,∠C=∠D,则∠A=∠F吗?请说明理由.
4.(2021·上海·七年级期中)如图,已知于点,于点,,试说明.
解:因为(已知),
所以( ).
同理.
所以( ).
即.
因为(已知),
所以( ).
所以( ).
5.(2021·上海·七年级期中)如图,已知,,是的平分线,,求的度数.
6.(2021·上海市浦东新区新场实验中学七年级期中)如图,ABCD,,,试说明:BCDE.请补充说明过程,并在括号内填上相应的理由.
解:∵ABCD(已知),
,
又(已知),
,
,
,
BCDE .
7.(2021·上海市西南模范中学七年级期中)如图,已知∠AED=∠C,∠DEF=∠B,试说明∠EFG+∠BDG=180 ,请完成下列填空:
∵∠AED=∠C (_________)
∴ED∥BC(_________)
∴∠DEF=∠EHC (___________)
∵∠DEF=∠B(已知)
∴_______(等量代换)
∴BD∥EH(同位角相等,两直线平行)
∴∠BDG=∠DFE(两直线平行,内错角相等)
∵_________________(邻补角的意义)
∴∠EFG+∠BDG=180 (___________)
8.(2021·上海·七年级期中)如图,已知,,试说明的理由.
解:把的对顶角记作,
所以(对顶角相等).
因为(已知),
所以( ),
所以 ( ).
(请继续完成接下去的说理过程)
9.(2021·上海松江·七年级期中)如图,已知射线AB与直线CD交于点O,OF平分∠BOC,AE∥DC,且∠A=70°,求∠DOF.
10.(2021·上海市川沙中学南校七年级期中)如图,已知,.说明的理由.
解:因为(已知)
所以______( )
所以( )
又因为(已知)
所以( )
又因为(已证)
所以( )
11.(2021··七年级期中)如图,直线AE、CF分别被直线EF、AC所截,已知∠1=∠2,AB平分∠EAC,CD平分∠ACG,将下列证明AB//CD的过程及理由填写完整.
证明:因为∠1=∠2,
所以 // ( ),
所以∠EAC=∠ACG( ),
因为AB平分∠EAC,CD平分∠ACG,
所以 =, =,
所以 = ,
所以AB//CD( ).
12.(2021·上海市浦东新区新场实验中学七年级期中)如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.
13.(2021·上海市川沙中学南校七年级期中)按照要求完成下列问题:
如图,直线和相交于点,点为上一点.
(1)过点作的垂线,交于点;
(2)过点作的垂线,交于点;
(3)比较线段和的大小:______.
14.(2021·上海市南洋模范初级中学七年级期中)如图,已知,,,求的度数.
15.(2021·上海市建平实验中学七年级期中)如图,AF、BD、CE是直线,点B在直线AC上,点E在直线DF上.∠A=∠F,∠C=∠D.
说明∠1与∠2互补的理由.
解:因为∠A=∠F(已知),
所以AC∥DF(_______________)
所以__________(_________________)
因为∠C=∠D(已知),
所以∠D=∠4(等量代换),
所以DB∥CE(______________________),
所以∠2+∠3=180°(_________________),
因为∠1=∠3(__________________),
所以∠2+∠1=180°(等量代换).
16.(2021·上海市第二初级中学七年级期中)如图,已知,点在的上方,则、、之间存在怎样的等量关系?说明理由.
解:过点做,
______(两直线平行,内错角相等),
(已知),
(已作),
____________(______).
17.(2021·上海市南洋模范初级中学七年级期中)如图,已知,,于点,那么与有什么数量关系?为什么?
18.(2021·上海杨浦·七年级期中)如图,已知AB∥CD,直线MN分别交直线AB、CD于点E、F,射线EG、FH分别平分∠AEF、∠DFE,试说明EG∥FH的理由.
解:因为AB∥CD(已知),
所以∠AEF=∠DFE( ),
因为射线EG、FH分别平分∠AEF、∠DFE(已知),
所以∠ =∠AEF,
∠ =∠EFD ( ).
所以 (等式性质).
所以EG∥FH( ).
19.(2021·上海杨浦·七年级期中)如图:∠1=∠2,∠D=90°,EF⊥CD,试说明∠3=∠B.
20.(2021·上海杨浦·七年级期中)如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB ( ),
所以∠1+ =180° ( ).
因为∠1=∠A(已知),
所以∠A+ =180° ( ).
所以DE∥AC ( ).
21.(2021··七年级期中)如图,已知直线AB//EF,AB//CD,∠ABE=50°,EC平分∠BEF,求∠DCE的度数.
22.(2021·上海·七年级期中)(1)探究:如图1,ABCDEF,试说明.
(2)应用:如图2,ABCD,点在、之间,与交于点,与交于点.若,,则的大小是多少?
(3)拓展:如图3,直线在直线、之间,且ABCDEF,点、分别在直线、上,点是直线上的一个动点,且不在直线上,连接、.若,则 度(请直接写出答案).
23.(2021·上海市罗南中学七年级期中)如图1,已知AB∥CD,直线AB、CD把平面分成①、②、③三个区域(直线AB、CD不属于①、②、③中任何一个区域).点P是直线AB、CD、AC外一点,联结PA、PC,可得∠PAB、∠PCD、∠APC.
(1)如图2,当点P位于第①区域一位置时,请填写∠APC=∠PAB+∠PCD的理由.
解:过点P作PE//AB,
因为AB//CD,PE//AB,
所以PE//CD( ).
因为PE//AB,
所以∠APE=∠PAB( ).
同理∠CPE=∠PCD.
因此∠APE+∠CPE=∠PAB+∠PCD.
即∠APC=∠PAB+∠PCD.
(2)在第(1)小题中改变点P的位置,如图3所示,求∠APC+∠PAB+∠PCD等于多少度?为什么?
(3)当点P在第②区域时,∠PAB、∠PCD、∠APC有怎样的数量关系?请画出图形,并直接写出相应的结论.
24.(2021·上海市南洋模范初级中学七年级期中)如图,AB、CD是两条直线,,.请说明的理由.
25.(2021·上海市教育学会青浦清河湾中学七年级期中)已知,直线AB∥CD
(1)如图(1),点G为AB、CD间的一点,联结AG、CG.若∠A=140°,∠C=150°,则∠AGC的度数是多少?
(2)如图(2),点G为AB、CD间的一点,联结AG、CG.∠A=x°,∠C=y°,则∠AGC的度数是多少?
(3)如图(3),写出∠BAE、∠AEF、∠EFG、∠FGC、∠GCD之间有何关系?直接写出结论.
26.(2021·上海市建平实验中学七年级期中)如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求三角形CAD的面积.
27.(2021·上海市罗南中学七年级期中)如图,已知∠ADC=∠ABC,DE、BF分别平分∠ADC和∠ABC,且DE∥BF,那么AB与DC平行吗?为什么?
28.(2021·上海松江·七年级期中)如图,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的理由.
解:因为AD⊥BC,EF⊥BC(______ )
所以∠ADC=90°,∠EFD=90°(______ )
得∠ADC=∠EFD(等量代换),
所以AD∥EF(______ )
得∠2+∠3=180°(______ )
由∠1+∠2=180°(______ )
得∠1=∠3(______ )
所以DG∥AB(______ )
所以∠CGD=∠CAB(______ )
29.(2021·上海·七年级期中)已知,点为平面内的一点,.
(1)当点在如图①的位置时,求与的数量关系.
解: .(根据如图填射线的画法)
因为,
所以 ( ).
所以(两直线平行,内错角相等);
(请继续完成接下去的说理过程)
(2)当点在如图②的位置时,与的数量关系是 (直接写出答案);
(3)在(2)的条件下,如图③,过点作,垂足为点,与的平分线分别交射线于点、,回答下列问题(直接写出答案):图中与相等的角是 , 度.
30.(2021·上海市民办文绮中学七年级期中)如图,D,E,G分别是AB,AC,BC边上的点,,.
(1)请说明的理由;
(2)若DE平分,,判断CD与EG的位置关系,并说明理由.
31.(2021··七年级期中)如图,已知,且,试说明的理由.
32.(2021·上海市第二初级中学七年级期中)如图所示,已知平分,,那么与相等吗?完成下面的填空.
平分(已知)
______(______),
(已知),
______(______),
____________(______),
(______).
33.(2021·上海市浦东新区新场实验中学七年级期中)请回答下列各题.
(1)探究:如图1,AB∥CD∥EF,试说明∠BCF=∠B+∠F.
(2)应用:如图2,AB∥CD,点F在AB、CD之间,FE与AB交于点M,FG与CD交于点N.若∠EFG=115°,∠EMB=55°,则∠DNG的大小是多少?
(3)拓展:如图3,直线CD在直线AB、EF之间,且AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连结QG、QH.若∠GQH=70°,则∠AGQ+∠EHQ=______度(请直接写出答案).
34.(2021·上海市建平实验中学七年级期中)(1)如图示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系; ②请说明理由.
35.(2021·上海杨浦·七年级期中)已知:AB∥CD,截线MN分别交AB、CD于点M、N.
(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足+(β﹣60)2=0,求∠BEM的度数;
(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;
(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为 (直接写出答案).
36.(2021·上海市民办文绮中学七年级期中)已知,点B为平面内一点,于B.
(1)如图,直接写出和之间的数量关系.
(2)如图,过点B作于点D,求证:.
(3)如图,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF那平分,BE平分,若,,求的度数.
37.(2021·上海市南洋模范初级中学七年级期中)(1)如图1,已知直线,在直线上取两点,为直线上的两点,无论点移动到任何位置都有:____________(填“>”、“<”或“=”)
(2)如图2,在一块梯形田地上分别要种植大豆(空白部分)和芝麻(阴影部分),若想把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变,请问应该怎么改进呢?写出设计方案,并在图中画出相应图形并简述理由.
(3)如图3,王爷爷和李爷爷两家田地形成了四边形,中间有条分界小路(图中折线),左边区域为王爷爷的,右边区域为李爷爷的。现在准备把两家田地之间的小路改为直路,请你用有关的几何知识,按要求设计出修路方案,并在图中画出相应的图形,说明方案设计理由。(不计分界小路与直路的占地面积).
38.(2021··七年级期中)问题情境:如图1,ABCD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:如图2,过P作PEAB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为 度;
(2)如图3,ADBC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
试卷第1页,共3页
参考答案:
1.,
【解析】
根据两直线平行,同位角相等求出∠EAD=∠B,再根据角平分线的定义可得∠DAC=∠EAD,然后利用两直线平行,内错角相等可得∠C=∠DAC.
∵(已知)
∴(两直线平行,同位角相等)
∵(已知)
∴(等量代换)
∵平分(已知)
∴(角平分线的意义)
∵(已知)
∴(两直线平行,内错角相等)
∴(等量代换)
∵(已证)
∴(等量代换)
【点睛】
本题主要考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.
2.角平分线的意义,平角的意义,∠IGD,∠EIB,等量代换,同位角相等,两直线平行
【解析】
根据题意和图形,可以写出解答过程中空格中需要填写的内容,本题得以解决.
解:因为GH是∠EGC的角平分线( 已知 )
所以∠EGH=∠HGC=56°(角平分线的意义)
因为CD是条直线
所以∠HGC+∠EGH+∠IGD=180°(平角的意义)
所以∠IGD=68°
因为∠EIB=68°
所以__∠IGD __=__∠EIB __(等量代换)
所以AB∥CD(同位角相等,两直线平行)
【点睛】
本题考查平行线的判定,解答本题的关键是明确题意,利用数形结合的思想解答.
3.∠A=∠F,理由见解析
【解析】
∠1+∠2=180°,∠2=∠AGC,∠1+∠AGC=180°,BD∥CE,有∠C=∠ABD=∠D,得DF∥AC,进而可说明∠A=∠F.
解:∠A=∠F,理由如下:
∵∠1+∠2=180°,∠2=∠AGC
∴∠1+∠AGC=180°
∴BD∥CE
∴∠C=∠ABD
∵∠C=∠D
∴∠D=∠ABD
∴DF∥AC
∴∠A=∠F.
【点睛】
本题考查了对顶角,平行线的判定与性质.解题的关键在利用角的数量关系证明直线平行.
4.垂直的定义;等量代换;等式的性质1;内错角相等,两直线平行
【解析】
根据垂直定义得出,求出,根据平行线的判定推出即可.
解:因为(已知),
所以(垂直的定义),
同理.
所以(等量代换),
即.
因为(已知),
所以(等式的性质,
所以(内错角相等,两直线平行).
故答案为:垂直的定义;等量代换;等式的性质1;内错角相等,两直线平行
【点睛】
本题考查了垂直定义和平行线的判定的应用,熟练掌握平行线的判定是解题关键.
5.
【解析】
根据平行线的性质求出∠BCE的度数,根据角平分线的性质求出∠BCN的度数,然后根据垂直的定义求出.
解:∵ ,,
∴,
∵是的平分线,
∴,
∵,
∴.
【点睛】
本题主要考查了平行线的性质、角平分线的定义和垂直的定义,熟知两直线平行,同位角相等,内错角相等,同旁内角互补是解题关键.
6.两直线平行,内错角相等;55;等量代换;已知;;同旁内角互补,两直线平行
【解析】
由题意根据平行线的性质与判定即可补充说理过程.
解:(已知),
(两直线平行,内错角相等),
又(已知),
(等量代换),
(已知),
,
(同旁内角互补,两直线平行).
故答案为:两直线平行,内错角相等;55;等量代换;已知;;同旁内角互补,两直线平行.
【点睛】
本题考查平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
7.已知;同位角相等,两直线平行;两直线平行,内错角相等;∠EHC =∠B;∠DFE+∠EFG =180 ;等量代换
【解析】
根据同位角相等,两直线平行推出ED∥BC,通过两直线平行,内错角相等推出∠DEF=∠EHC,再运用等量代换得到∠EHC =∠B,最后推出BD∥EH,∠BDG=∠DFE,再利用邻补角的意义推出结论,据此回答问题.
解:∵∠AED=∠C (已知)
∴ED∥BC(同位角相等,两直线平行)
∴∠DEF=∠EHC (两直线平行,内错角相等)
∵∠DEF=∠B(已知)
∴∠EHC =∠B (等量代换)
∴BD∥EH(同位角相等,两直线平行)
∴∠BDG=∠DFE(两直线平行,内错角相等)
∵∠DFE+∠EFG =180 (邻补角的意义)
∴∠EFG+∠BDG=180 (等量代换).
【点睛】
本题主要考查平行线的判定和性质,属于综合题,难度一般,熟练掌握平行线的判定和性质是解题关键.
8.等量代换;BD;CE;同位角相等,两直线平行;见解析
【解析】
根据平行线的判定与性质求解即可.
解:把的对顶角记作,
所以(对顶角相等).
因为(已知),
所以(等量代换),
所以(同位角相等,两直线平行),
所以(两直线平行,同位角相等),
又因为,
所以(同位角相等,两直线平行),
所以(两直线平行,内错角相等),
所以(等量代换).
故答案为:等量代换;;;同位角相等,两直线平行.
【点睛】
本题主要考查了平行线的性质与判定的综合应用,熟练掌握平行线的性质与判定方法是解答本题的关键.解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
9.145°
【解析】
根据平行线的性质,两直线平行,同位角相等可得∠A=∠BOC=70°,由角平分线的性质可得∠BOF=∠FOC=35°,再根据平角的性质即可得出答案.
解:∵AE∥DC,
∴∠A=∠BOC=70°,
又∵OF平分∠BOC,
∴∠BOF=∠FOC=35°,
∴∠DOF=180°-∠FOC=180°-35°=145°.
【点睛】
本题主要考查了平行线的性质、邻补角的概念等,熟练应用平行线的性质进行求解是解决本题的关键.
10.CD;内错角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;等量代换
【解析】
根据平行线的判定与性质解答即可.
解:因为(已知),
所以CD(内错角相等,两直线平行),
所以(两直线平行,内错角相等),
又因为(已知),
所以(两直线平行,同位角相等),
又因为(已证),
所以(等量代换),
故答案为:CD;内错角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;等量代换.
【点睛】
本题考查平行线的判定与性质,熟练掌握平行线的判定与性质,能正确写出每一步结论的依据是解答的关键.
11.AE;FG;同位角相等,两直线平行;两直线平行,内错角相等;∠3;∠4;∠3;∠4;内错角相等,两直线平行
【解析】
利用平行线的判定及性质就可求得本题.即同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行.反之即为性质.
证明:因为∠1=∠2,
所以AE∥CF(同位角相等,两直线平行),
所以∠EAC=∠ACG(两直线平行,内错角相等),
因为AB平分∠EAC,CD平分∠ACG,
所以∠3=∠EAC,∠4=∠ACG,
所以∠3=∠4,
所以AB∥CD(内错角相等,两直线平行).
故答案为:AE;FG;同位角相等,两直线平行;两直线平行,内错角相等;∠3;∠4;∠3;∠4;内错角相等,两直线平行.
【点睛】
本题主要考查了平行线的判定和性质.正确的识别图形是解题的关键.
12.证明见解析.
【解析】
根据平行线的判定与性质即可证明.
∵AD⊥BC,EF⊥BC,
∴AD∥EF,∴∠1+∠2=180°,
∵∠2+∠3=180°,∴∠1=∠3
∴AB∥DG,
∴∠GDC=∠B.
【点睛】
此题主要考查平行线的性质与判定,解题的关键是熟知平行线的判定.
13.(1)作图见详解;(2)作图见详解;(3).
【解析】
(1)、(2)利用题中几何语言画出对应的几何图形即可;
(3)根据垂线段最短求解即可.
解:(1)如图,为所作;
(2)如图,为所作;
(3)利用垂线段最短可判断.
【点睛】
本题考查了作图-基本作图,垂线段最短的性质,熟悉相关性质是解题的关键.
14.
【解析】
利用“两直线平行,同旁内角互补”列方程求解即可.
解:,,
即得,解得.
【点睛】
本题考查了平行线的性质,掌握“两直线平行,同旁内角互补”的性质是解题关键.
15.内错角相等,两直线平行;∠4=∠C;两直线平行,内错角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;对顶角相等
【解析】
由∠A=∠F ,可得AC∥DF,从而∠4=∠C,又由∠C=∠D,可得∠D=∠4,得到DB∥CE ,从而∠2+∠3=180°,再由对顶角相等,即可求解.
解:因为∠A=∠F(已知),
所以AC∥DF( 内错角相等,两直线平行 )
所以∠4=∠C( 两直线平行,内错角相等 )
因为∠C=∠D(已知),
所以∠D=∠4(等量代换),
所以DB∥CE( 同位角相等,两直线平行 ),
所以∠2+∠3=180°( 两直线平行,同旁内角互补 ),
因为∠1=∠3( 对顶角相等 ),
所以∠2+∠1=180°(等量代换).
【点睛】
本题主要考查了平行线的判定和性质,对顶角的定义,熟练掌握平行线的判定和性质是解题的关键.
16.,理由见解析;,,,平行于同一条直线的两条直线平行
【解析】
根据平行线的性质得,根据平行于同一条直线的两条直线平行得,根据平行线的性质得,根据角之间的关系等量代换即可得.
解:过点E作,
∴(两直线平行,内错角相等),
∴(已知),
(已知),
∴(平行于同一条直线的两条直线平行),
∴,
∵,
∴.
【点睛】
本题考查了平行线的性质,解题的关键是掌握平行线的性质.
17.∠4与∠5互余,理由见解析
【解析】
由题意知∠2+∠3=90°,∠1+∠4=90°,∠2+∠4=90°,∠2=∠5,得到∠5+∠4=90°,进而可判断两角关系.
解:∠4与∠5互余,
理由:∵OE⊥OA,
∴∠AOE=90°,即∠2+∠3=90°,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠4=90°
∵∠1=∠2,
∴∠2+∠4=90°,
∵,∴∠2=∠5,
∴∠5+∠4=90°,即∠4与∠5互余.
【点睛】
本题考查了同角的余角相等,平行线的性质.解题的关键在于找出角度的数量关系.
18.两直线平行内错角相等;GEF;EFH;角平分线的定义;∠GEF=∠EFH;内错角相等两直线平行.
【解析】
根据平行线的性质、角平分线的定义及平行线的判定逐一求解即可.
解:因为AB∥CD(已知),
所以∠AEF=∠DFE(两直线平行内错角相等),
因为射线EG、FH分别平分∠AEF、∠DFE(已知),
所以∠GEF=∠AEF,
∠EFH=∠EFD (角平分线的定义).
所以∠GEF=∠EFH(等式性质).
所以EG∥FH(内错角相等两直线平行).
故答案为:两直线平行内错角相等;GEF;EFH;角平分线的定义;∠GEF=∠EFH;内错角相等两直线平行.
【点睛】
本题主要考查了平行线的判定与性质,准确判断是解题的关键.
19.见解析
【解析】
因为∠1=∠2,由内错角相等证明AD∥BC,又因为∠D=90°,EF⊥CD,则有AD∥EF,所以EF∥BC,故可求证∠3=∠B.
解:∵∠1=∠2,
∴AD∥BC,
∵∠D=90°,
∴AD⊥CD,
∵EF⊥CD,
∴AD∥EF,
∴EF∥BC,
∴∠3=∠B.
【点睛】
本题主要考查了平行线的判定与性质,准确计算是解题的关键.
20.已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行
【解析】
根据平行线的判定、等量代换及平行线的判定逐一求解即可.
解:因为DF∥AB (已知),
所以∠1+∠DEA=180° (两直线平行同旁内角互补).
因为∠1=∠A(已知),
所以∠A+∠DEA=180° (等量代换).
所以DE∥AC (同旁内角互补两直线平行).
故答案为:已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行.
【点睛】
本题主要考查了平行线的判定与性质,准确判断是解题的关键.
21.∠DCE=155°
【解析】
利用平行线的性质、平行公理及角平分线的定义即可求解.
解:∵AB//EF,∠ABE=50°(已知)
∴∠ABE=∠BEF=50°(两直线平行,内错角相等)
∵EC平分∠BEF(已知)
∴∠CEF=∠BEF=25°(角平分线的意义)
∵AB//EF,AB//CD(已知)
∴CD//EF(平行线的传递性)
∴∠CEF+∠DCE=180°(两直线平行,同旁内角互补)
∴∠DCE=180°-25°=155°(等式性质).
【点睛】
本题考查了平行线的性质、平行公理及角平分线的定义,熟练掌握有关定理、定义是解题的基础.
22.(1)见解析;(2)60°;(3)70或290
【解析】
(1)由可得,,,则;
(2)利用(1)中的结论可知,,则可得的度数为,由对顶角相等可得;
(3)结合(1)中的结论可得,注意需要讨论是钝角或是锐角时两种情况.
解:(1)如图1,,
,,
,
.
(2)由(1)中探究可知,,
,且,
,
;
(3)如图,当为钝角时,
由(1)中结论可知,,
;
当为锐角时,如图,
由(1)中结论可知,,
即,
综上,或.
故答案为:70或290.
【点睛】
本题主要考查平行线的性质与判定,难度适中,观察图形,推出角之间的和差关系是解题关键.
23.(1)平行的传递性;两直线平行,内错角相等;
(2)360°,理由见解析;
(3)∠PCD =∠PAB+∠APC,见解析.
【解析】
(1)根据平行线的性质解题;
(2)过点P作PE//AB,由两直线平行,同旁内角相等解得∠APE+∠PAB=180°,∠EPC+∠PCD=180°,再根据∠APC+∠PAB+∠PCD=∠APE+∠EPC+∠PAB+∠PCD解题;
(3)根据题意,画出图形,再由两直线平行,内错角相等得到∠APE=∠PAB,∠PCD=∠CPE,结合∠CPE=∠APE+∠APC解题.
(1)
解:因为AB//CD,PE//AB,
所以PE//CD(平行的传递性)
因为PE//AB,
所以∠APE=∠PAB(两直线平行,内错角相等).
故答案为:平行的传递性;两直线平行,内错角相等;
(2)
∠APC+∠PAB+∠PCD=360°,
见解析:
过点P作PE//AB,
所以∠APE+∠PAB=180°,
因为PE//CD,
所以∠EPC+∠PCD=180°,
所以∠APC+∠PAB+∠PCD=∠APE+∠EPC+∠PAB+∠PCD=180°+180°=360°;
(3)
∠PCD =∠PAB+∠APC,理由如下,
当点P在第②区域时,如图,
过点P作PE//AB,
所以∠APE=∠PAB,
因为PE//CD,
所以∠PCD=∠CPE
因为∠CPE=∠APE+∠APC
所以∠PCD =∠PAB+∠APC.
【点睛】
本题考查平行线的拐角问题、平行线的性质等知识,是重要考点,掌握相关知识是解题关键.
24.见解析
【解析】
根据平行线的判定得出AB∥CD,根据平行线的性质得出∠AMN=∠MND,求出∠EMN=∠MNF,根据平行线的判定得出ME∥NF,根据平行线的性质得出即可.
∵∠BMN=∠CNM(已知),
∴(内错角相等,两直线平行).
∴∠AMN=∠MND(两直线平行,内错角相等).
∵∠1=∠2(已知),
∴∠EMN=∠MNF(等式性质).
∴(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等),
【点睛】
本题考查了平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.
25.(1)70°;(2)∠AGC=(x+y)°;(3)∠BAE+∠EFG+∠GCD=∠AEF+∠FGC.
【解析】
(1)过点G作GE∥AB,利用平行线的性质即可进行转化求解.
(2)过点G作GF∥AB,利用平行线的性质即可进行转化求解.
(3)过点E作EM∥AB,过点F作FN∥AB,过点G作GQ∥CD,利用平行线的性质即可进行转化找到角的关系.
解:(1)如图,过点G作GE∥AB,
∵AB∥GE,
∴∠A+∠AGE=180°(两直线平行,同旁内角互补).
∵∠A=140°,
∴∠AGE=40°.
∵AB∥GE,AB∥CD,
∴GE∥CD.
∴∠C+∠CGE=180°(两直线平行,同旁内角互补).
∵∠C=150°,
∴∠CGE=30°.
∴∠AGC=∠AGE+∠CGE=40°+30°=70°.
(2)如图,过点G作GF∥AB
∵AB∥GF,
∴∠A=AGF(两直线平行,内错角相等).
∵AB∥GF,AB∥CD,
∴GF∥CD.
∴∠C=∠CGF.
∴∠AGC=∠AGF+∠CGF=∠A+∠C .
∵∠A=x°,∠C=y°,
∴∠AGC=(x+y)°.
(3)如图所示,过点E作EM∥AB,过点F作FN∥AB,过点G作GQ∥CD,
∵AB∥CD,
∴AB∥EM∥FN∥GQ∥CD.
∴∠BAE=∠AEM,∠MEF=∠EFN,∠NFG=∠FGQ,∠QGC=∠GCD(两直线平行,内错角相等).
∴∠AEF=∠BAE+∠EFN,∠FGC=∠NFG+GCD.
∵∠EFN+∠NFG=∠EFG,
∴∠BAE+∠EFG+∠GCD=∠AEF+∠FGC.
【点睛】
本题考查平行线的判定与性质,本题构造辅助线利用平行线的传递性结合平行线性质是解题关键.
26.6
【解析】
结合题意,根据平行线的性质,得ADBC;AD到BC的距离设为a,根据三角形面积公式和代数式的性质,得,从而完成求解.
∵∠1=∠2
∴ ADBC(内错角相等,两直线平行),
AD到BC的距离设为a,
∴三角形ABC面积==3,
∴
∵AD=2BC
∴三角形ACD面积==6.
【点睛】
本题考查了平行线、代数式的知识;结果的关键是熟练掌握平行线、代数式的性质,从而完成求解.
27.AB∥DC,理由见解析.
【解析】
根据平行线的性质推出∠DEA=∠FBA,再根据角平分线性质推出∠CDE=∠FBA,等量代换得到∠CDE=∠DEA,根据平行线的判定推出即可.
解:AB∥DC,理由如下:
∵DE∥BF,
∴∠DEA=∠FBA,
∵∠ADC=∠ABC,DE、BF分别平分∠ADC和∠ABC,
∴∠CDE=∠CDA=∠CBA=∠FBA=∠DEA,
∴AB∥DC.
【点睛】
本题主要考查对平行线的性质和判定,角平分线性质等知识点的理解和掌握,能推出∠CDE=∠DEA是解此题的关键.
28.已知 垂直定义 同位角相等,两直线平行 两直线平行,同旁内角互补 已知 同角的补角相等 内错角相等,两直线平行 两直线平行,同位角相等
【解析】
求出AD∥EF,根据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,根据平行线的判定得出DG∥AB,根据平行线的性质得出∠CGD=∠CAB即可.
解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=90°,∠EFC=90°(垂直定义),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
【点睛】
本题考查了平行线的性质和判定,垂直定义,补角的性质,能综合运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之即为平行线的判定.
29.(1)过点作;;;;如果一条直线和两条平行线中的一条平行,那么它和另一条也平行;见解析
(2)
(3),45
【解析】
(1)过点作,先根据平行线的判定与性质可得,,再根据角的和差、等量代换即可得出结论;
(2)过点作,先根据平行线的判定与性质可得,,再根据、角的和差即可得出结论;
(3)过点作,先根据平行线的判定与性质可得,从而可得,再结合(2)的结论可得,然后根据角平分线的定义可得,最后根据即可得出答案
(1)
解:如图①,过点作,
,
(如果一条直线和两条平行线中的一条平行,那么它和另一条也平行).
.
,
.
.
,
.
.
(2)
解:如图②,过点作,
.
,
.
.
,
.
.
.
故答案为:.
(3)
解:如图③,过点作,
,
,
.
,
,
.
.
,
由(2)已得:,
;
平分,
.
平分,
.
,
故答案为:,45.
【点睛】
本题考查了平行线的判定与性质,角平分线的定义等知识点,通过作辅助线,构造平行线是解题关键.
30.(1)证明见解析;
(2),证明见解析.
【解析】
(1)根据已知条件和对顶角相等可证明ABEG,再根据平行线的性质得角相等,再等量代换可得∠3=∠EGC,进而可得DE BC;
(2)根据已知条件可得∠B=45°,可以证明CD⊥AB,再由ABEG,即可得CD⊥EG.
(1)
解:∵,,
∴,
∴,
∴.
又∵,
∴,
∴;
(2)
∵DE平分,
∴.
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,
∴.
【点睛】
本题考查了平行线的判定与性质,解决本题的关键是区别平行线的判定与性质并熟练运用.
31.详见解析
【解析】
由CD∥AB,可得,由,由等量代换可得,即可完成证明.
证明:∵(已知)
∴(两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行)
【点睛】
本题考查了平行线的性质和判定,解题的关键是通过图形分析证明思路.
32.3;角平分线的定义;3;等量代换;内错角相等,两直线平行;两直线平行,同位角相等
【解析】
根据题目给定的思路分析题意,利用平行线的判定和性质进行证明,并填写证明依据即可.
平分(已知)
(角平分线的定义),
(已知),
(等量代换),
(内错角相等,两直线平行),
(两直线平行,同位角相等).
【点睛】
本题主要考查了平行线的判定和性质,解题的关键是区分其关系.
33.(1)证明见解析
(2)60°
(3)70或290
【解析】
(1)由 可得,∠B=∠BCD,∠F=∠DCF,从而可以证明结论成立;
(2)由∠MFN=∠AMF+∠CNF,则可得∠CNF的度数为60°,由对顶角相等可得;
(3)分两种情况讨论,即∠AGQ是钝角与∠AGQ是锐角时.
(1)
证明:∵AB∥CD,
∴∠B=∠BCD.(两直线平行内错角相等),
同理可证,∠F=∠DCF.
∵∠BCF=∠BCD+∠DCF,
∴∠BCF=∠B+∠F.(等量代换)
(2)
解:由探究可知:∠MFN=∠AMF+∠CNF,∠MFN=115°,,
∴∠CNF=∠DNG=115°-55°=60°.
故答案为:60°.
(3)
如图3中,当点Q在直线GH的右侧时,
∵AB∥CD∥EF,
∴∠AGQ+∠GQC=180°,∠CQH+∠EHQ=180°,
即∠AGQ+∠GQH+∠EHQ=180°,
∴∠AGQ+∠EHQ=360°-70°=290°,
当点Q在直线GH的左侧时,由(1)的结论可得:
.
故答案为:70或290.
【点睛】
本题主要考查平行线的性质与判定,熟练运用平行线的性质是解题关键.
34.(1)证明见解析;(2)∠1+∠2-∠E=180°.
【解析】
(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1,由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
解:(1)过点E作EF∥AB,
∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),
∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),
∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),
∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.
【点睛】
本题考查了平行线的性质,作辅助线并熟记性质是解题的关键.
35.(1)30°;(2)∠DEF+2∠CDF=150°,理由见解析;(3)
【解析】
(1)由非负性可求α,β的值,由平行线的性质和外角性质可求解;
(2)过点E作直线EH∥AB,由角平分线的性质和平行线的性质可求∠DEF=180°﹣30°﹣2x°=150°﹣2x°,由角的数量可求解;
(3)由平行线的性质和外角性质可求∠PMB=2∠Q+∠PCD,∠CPM=2∠Q,即可求解.
解:(1)∵+(β﹣60)2=0,
∴α=30,β=60,
∵AB∥CD,
∴∠AMN=∠MND=60°,
∵∠AMN=∠B+∠BEM=60°,
∴∠BEM=60°﹣30°=30°;
(2)∠DEF+2∠CDF=150°.
理由如下:过点E作直线EH∥AB,
∵DF平分∠CDE,
∴设∠CDF=∠EDF=x°;
∵EH∥AB,
∴∠DEH=∠EDC=2x°,
∴∠DEF=180°﹣30°﹣2x°=150°﹣2x°;
∴∠DEF=150°﹣2∠CDF,
即∠DEF+2∠CDF=150°;
(3)如图3,设MQ与CD交于点E,
∵MQ平分∠BMT,QC平分∠DCP,
∴∠BMT=2∠PMQ,∠DCP=2∠DCQ,
∵AB∥CD,
∴∠BME=∠MEC,∠BMP=∠PND,
∵∠MEC=∠Q+∠DCQ,
∴2∠MEC=2∠Q+2∠DCQ,
∴∠PMB=2∠Q+∠PCD,
∵∠PND=∠PCD+∠CPM=∠PMB,
∴∠CPM=2∠Q,
∴∠Q与∠CPM的比值为,
故答案为:.
【点睛】
本题主要考查了平行线的性质、角平分线的性质,准确计算是解题的关键.
36.(1)
(2)证明见解析
(3)
【解析】
(1)根据平行线的性质及直角三角形的性质证明即可;
(2)过点B作,根据同角的余角相等得出,再根据平行线的性质得到,即可得到;
(3)过点B作,根据角平分线的定义得出,设,,可得,再根据,得到,解方程得到,继而得出,.
(1)
如图1,
∵,
∴,
∵,
∴,
∴,,
故答案为:;
(2)
如图2,过点B作,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,.
(3)
如图3,过点B作,
∵BF平分,BE平分,
∴,,
由(2)知,
∴,设,,
则,,,
,
∴
∵,,
∴,
中,由得
,
∵,
∴,
∴,
∴,
∴.
【点睛】
本题考查平行线的性质与应用、角平分线的性质、方程思想等知识,学会添加辅助线,掌握相关知识是解题关键.
37.(1);(2)见解析;(3)见解析
【解析】
(1)根据平行线间的距离处处相等,所以无论点在m上移动到何位置,总有与同底等高,因此它们的面积相等;
(2)利用同底等高的三角形的面积相等即可求得设计方案;
(3)连结,过点作的平行线,连结或,则或即为所修直路.
(1)∵与有共同的边AB,
又∵,
∴与的高相等,即与同底等高,
∴=,
故答案为:=;
(2)方法一:
连结,将的区域用于种植大豆,的区域用于种植芝麻,理由如下:
在梯形ABCD中,,
则与同底等高,
∴,
∴,
即,
又由可知与同底等高,
∴,
∴该设计方案把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变;
方法二
连结,将的区域用于种植大豆,的区域用于种植芝麻,理由如下:
在梯形ABCD中,,
则与同底等高,
∴,
∴,
即,
又由可知与同底等高,
∴,
∴该设计方案把种植大豆的两块地改为一块地,且使分别种植两种植物的面积不变;
(3)方法一
连结,过点作的平行线:连结,即为所修直路.
将四边形的区域分给王爷爷,四边形的区域分给李爷爷,理由如下:
∵,则与同底等高,
∴,则,
即,
又由可知与同底等高,
∴,
∴满足修路方案;
方法二:
连结,过点作的平行线:连结,即为所修直路.
将四边形的区域分给王爷爷,四边形的区域分给李爷爷,理由如下:
∵,则与同底等高,
∴,则,
即,
又由可知与同底等高,
∴,
∴满足修路方案.
【点睛】
本题主要考查了两条平行线间的距离处处相等.只要两个三角形是同底等高的,则两个三角形的面积一定相等.解题的关键还要根据等式的性质进一步进行变形.
38.(1)110°;(2)∠CPD=∠α+∠β,见解析;(3)当P在BA延长线时,∠CPD=∠β-∠α;当P在AB延长线上时,∠CPD=∠α-∠β
【解析】
(1)过P作PEAB,通过平行线性质求∠APC即可;
(2)过P作PEAD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(3)画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
解:(1)过点P作PEAB,
∵ABCD,
∴PEABCD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°;
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵ADBC,
∴ADPEBC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,∠CPD=∠β-∠α,
理由是:如图4,过P作PEAD交CD于E,
∵ADBC,
∴ADPEBC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE-∠DPE =∠β-∠α;
当P在AB延长线时,∠CPD=∠α-∠β,
理由是:如图5,过P作PEAD交CD于E,
∵ADBC,
∴ADPEBC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE -∠CPE =∠α-∠β.
【点睛】
本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较典型的题目,分类讨论是解题的关键.
答案第1页,共2页
同课章节目录
