2021-2022学年人教版八年级下册数学 18.1平行四边形 知识点过关练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学 18.1平行四边形 知识点过关练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 371.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 20:10:08 | ||
图片预览


文档简介
人教版八年级下册数学《平行四边形》知识点过关练习
(考查范围:18.1平行四边形)
总分:120分 建议用时:90分钟
一、选择题(30分)。
题号 1 2 3 4 5 6 7 8 9 10
选项
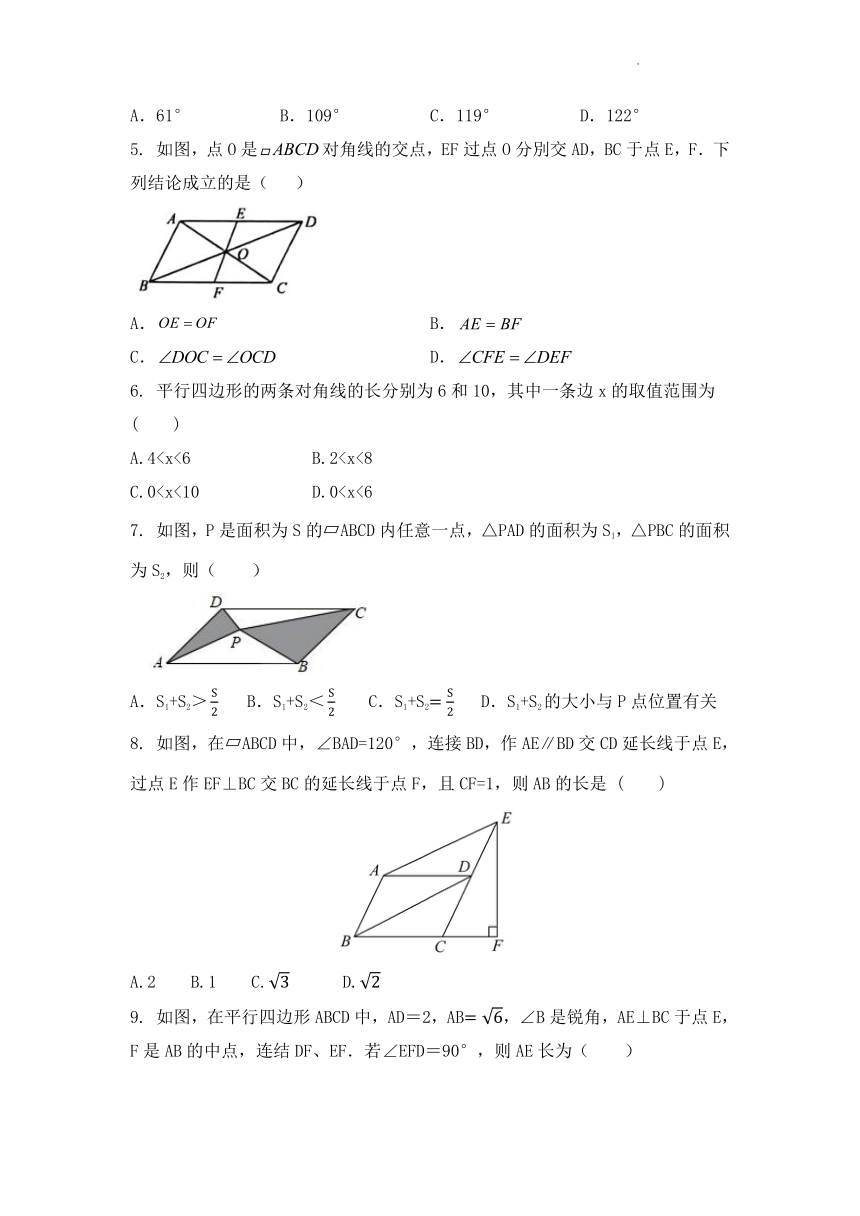
1.以下平行四边形的性质错误的是 ( )
A.对边平行 B.对角相等
C.对边相等 D.对角线互相垂直
2. 如图,的顶点A,B,C的坐标分别是,则顶点D的坐标是( )
A. B. C. D.
3. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
4. 如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
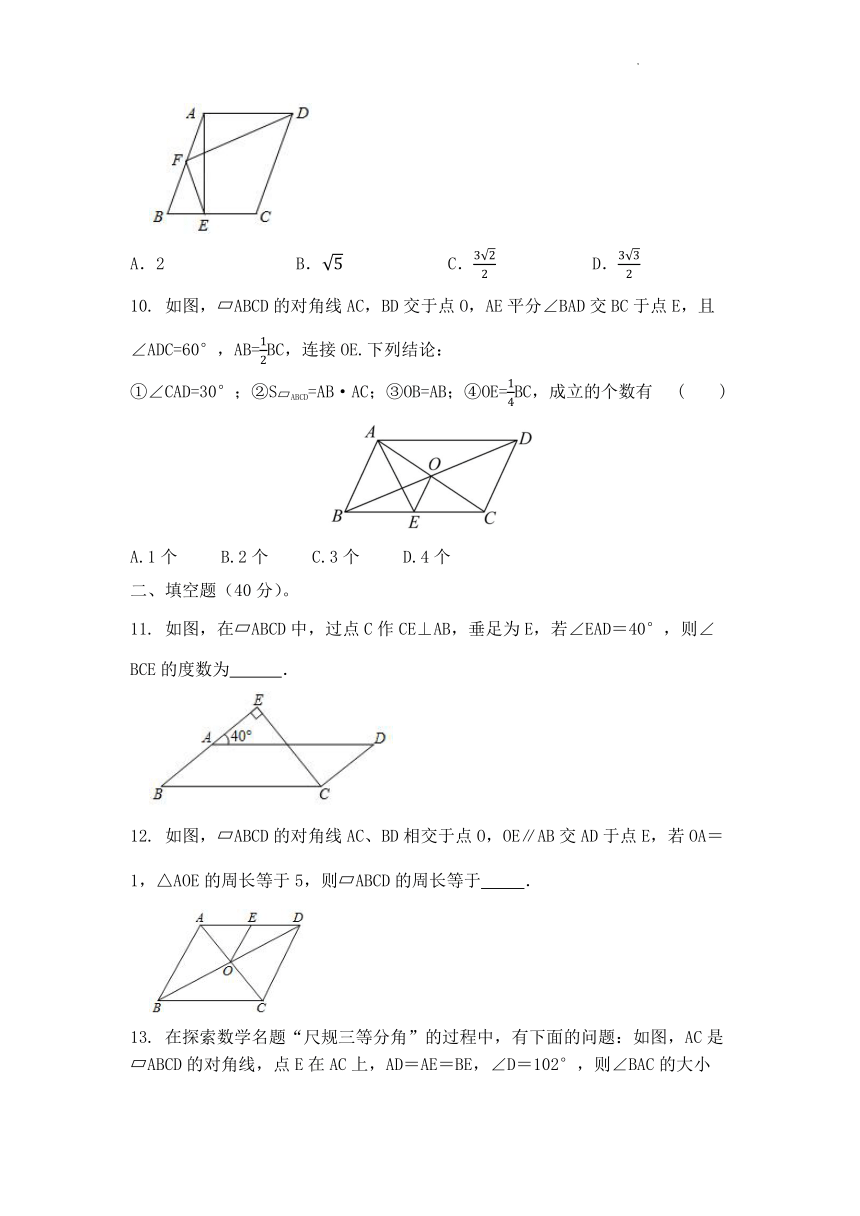
5. 如图,点O是对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )
A. B.
C. D.
6. 平行四边形的两条对角线的长分别为6和10,其中一条边x的取值范围为
( )
A.4C.07. 如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( )
A.S1+S2 B.S1+S2 C.S1+S2 D.S1+S2的大小与P点位置有关
8. 如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 ( )
A.2 B.1 C. D.
9. 如图,在平行四边形ABCD中,AD=2,AB,∠B是锐角,AE⊥BC于点E,F是AB的中点,连结DF、EF.若∠EFD=90°,则AE长为( )
A.2 B. C. D.
10. 如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且
∠ADC=60°,AB=BC,连接OE.下列结论:
①∠CAD=30°;②S ABCD=AB·AC;③OB=AB;④OE=BC,成立的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(40分)。
11. 如图,在 ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠
BCE的度数为 .
12. 如图, ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=
1,△AOE的周长等于5,则 ABCD的周长等于 .
13. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是
ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小
是 .
14. 如图,在中,点E在上,且平分,若,,则的面积为________.
15. 如图, ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,使点A正好落在CD上的F点,若△FDE的周长为8cm,△FCB的周长为20cm,则FC的长为________cm.
16. 如图,在平行四边形ABCD中,AB=,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为__________.
17. 如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD,CB重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是________.
18. 如图,在 ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动
点,连接ED并延长至点F,使得DFDE,以EC、EF为邻边构造 EFGC,连接
EG,则EG的最小值为 .
三、解答题(50分)。
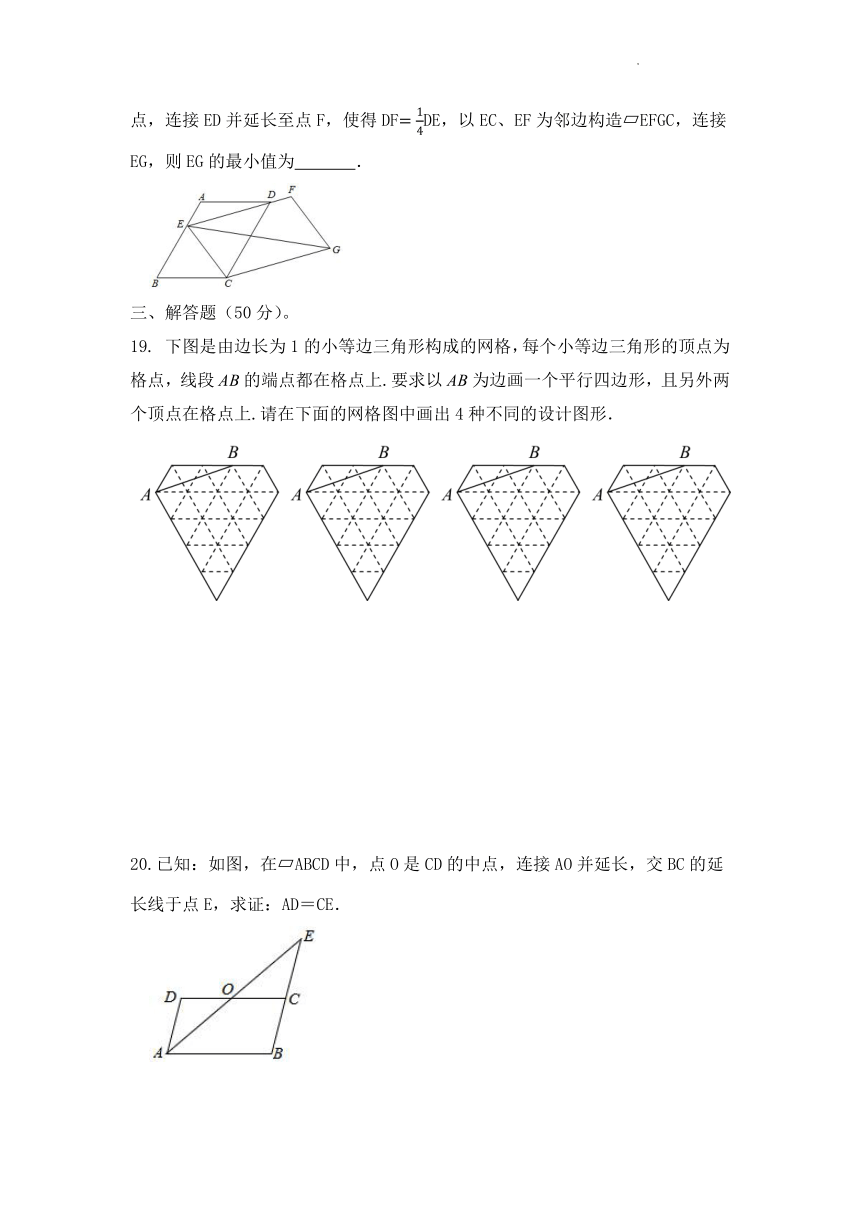
19. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.
20.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延
长线于点E,求证:AD=CE.
21. 已知 ABCD,O为对角线AC的中点,过O的一条直线交AD于点E,交BC于
点F.
(1)求证:△AOE≌△COF;
(2)若AE:AD=1:2,△AOE的面积为2,求 ABCD的面积.
22. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为
OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
23. 如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
人教版八年级下册数学《平行四边形》靶向专题复习集训
(18.1的平行四边形专题练)(答案版)
总分:120分 建议用时:90分钟
一、选择题(30分)。
题号 1 2 3 4 5 6 7 8 9 10
选项
1以下平行四边形的性质错误的是 ( )
A.对边平行 B.对角相等
C.对边相等 D.对角线互相垂直
选:D.
2. 如图,的顶点A,B,C的坐标分别是,则顶点D的坐标是( )
A. B. C. D.
选:C
3. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
选:C.
4. 如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
选:C
5. 如图,点O是对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )
A. B.
C. D.
选:A
6. 平行四边形的两条对角线的长分别为6和10,其中一条边x的取值范围为
( )
A.4C.0选B.
7. 如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( )
A.S1+S2 B.S1+S2 C.S1+S2 D.S1+S2的大小与P点位置有关
选:C.
8. 如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 ( )
A.2 B.1 C. D.
选:B.
9. 如图,在平行四边形ABCD中,AD=2,AB,∠B是锐角,AE⊥BC于点E,F是AB的中点,连结DF、EF.若∠EFD=90°,则AE长为( )
A.2 B. C. D.
选:B
10. 如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且
∠ADC=60°,AB=BC,连接OE.下列结论:
①∠CAD=30°;②S ABCD=AB·AC;③OB=AB;④OE=BC,成立的个数有 ( C )
A.1个 B.2个 C.3个 D.4个
选:C.
二、填空题(40分)。
11. 如图,在 ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠BCE的度数为 .
答案为:50°.
12. 如图, ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则 ABCD的周长等于 .
答案为:16.
13. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是
ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小
是 .
答案为:26°
14. 如图,在中,点E在上,且平分,若,,则的面积为________.
【答案】50
15. 如图, ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,使点A正好落在CD上的F点,若△FDE的周长为8cm,△FCB的周长为20cm,则FC的长为________cm.
答案:6
16. 如图,在平行四边形ABCD中,AB=,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为__________.
答案:3
17. 如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD,CB重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是________.
答案:26
18. 如图,在 ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动
点,连接ED并延长至点F,使得DFDE,以EC、EF为邻边构造 EFGC,连接
EG,则EG的最小值为 .
答案为:9.
三、解答题(50分)。
19. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.
解:如图,四边形ABCD是平行四边形.
20.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延长线于点E,求证:AD=CE.
证明:∵O是CD的中点,
∴OD=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
,
∴△AOD≌△EOC(ASA),
21. 已知 ABCD,O为对角线AC的中点,过O的一条直线交AD于点E,交BC于
点F.
(1)求证:△AOE≌△COF;
(2)若AE:AD=1:2,△AOE的面积为2,求 ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴OA=OC,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA);
(2)∵AE:AD=1:2,O为对角线AC的中点,
∴AO:AC=1:2,
∵∠EAO=∠DAC,
∵△AOE的面积为2,
∴△ADC的面积为8,
∴平行四边形ABCD的面积为16.
22. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为
OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
23. 如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠ADC=∠CBA,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)当BD平分∠ABC时,四边形AFCE是菱形,
理由:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
∴AC⊥EF,
∵DE=BF,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形.
(考查范围:18.1平行四边形)
总分:120分 建议用时:90分钟
一、选择题(30分)。
题号 1 2 3 4 5 6 7 8 9 10
选项
1.以下平行四边形的性质错误的是 ( )
A.对边平行 B.对角相等
C.对边相等 D.对角线互相垂直
2. 如图,的顶点A,B,C的坐标分别是,则顶点D的坐标是( )
A. B. C. D.
3. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
4. 如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
5. 如图,点O是对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )
A. B.
C. D.
6. 平行四边形的两条对角线的长分别为6和10,其中一条边x的取值范围为
( )
A.4
A.S1+S2 B.S1+S2 C.S1+S2 D.S1+S2的大小与P点位置有关
8. 如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 ( )
A.2 B.1 C. D.
9. 如图,在平行四边形ABCD中,AD=2,AB,∠B是锐角,AE⊥BC于点E,F是AB的中点,连结DF、EF.若∠EFD=90°,则AE长为( )
A.2 B. C. D.
10. 如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且
∠ADC=60°,AB=BC,连接OE.下列结论:
①∠CAD=30°;②S ABCD=AB·AC;③OB=AB;④OE=BC,成立的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(40分)。
11. 如图,在 ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠
BCE的度数为 .
12. 如图, ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=
1,△AOE的周长等于5,则 ABCD的周长等于 .
13. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是
ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小
是 .
14. 如图,在中,点E在上,且平分,若,,则的面积为________.
15. 如图, ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,使点A正好落在CD上的F点,若△FDE的周长为8cm,△FCB的周长为20cm,则FC的长为________cm.
16. 如图,在平行四边形ABCD中,AB=,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为__________.
17. 如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD,CB重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是________.
18. 如图,在 ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动
点,连接ED并延长至点F,使得DFDE,以EC、EF为邻边构造 EFGC,连接
EG,则EG的最小值为 .
三、解答题(50分)。
19. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.
20.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延
长线于点E,求证:AD=CE.
21. 已知 ABCD,O为对角线AC的中点,过O的一条直线交AD于点E,交BC于
点F.
(1)求证:△AOE≌△COF;
(2)若AE:AD=1:2,△AOE的面积为2,求 ABCD的面积.
22. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为
OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
23. 如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
人教版八年级下册数学《平行四边形》靶向专题复习集训
(18.1的平行四边形专题练)(答案版)
总分:120分 建议用时:90分钟
一、选择题(30分)。
题号 1 2 3 4 5 6 7 8 9 10
选项
1以下平行四边形的性质错误的是 ( )
A.对边平行 B.对角相等
C.对边相等 D.对角线互相垂直
选:D.
2. 如图,的顶点A,B,C的坐标分别是,则顶点D的坐标是( )
A. B. C. D.
选:C
3. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OB=OD
选:C.
4. 如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A.61° B.109° C.119° D.122°
选:C
5. 如图,点O是对角线的交点,EF过点O分別交AD,BC于点E,F.下列结论成立的是( )
A. B.
C. D.
选:A
6. 平行四边形的两条对角线的长分别为6和10,其中一条边x的取值范围为
( )
A.4
7. 如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( )
A.S1+S2 B.S1+S2 C.S1+S2 D.S1+S2的大小与P点位置有关
选:C.
8. 如图,在 ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是 ( )
A.2 B.1 C. D.
选:B.
9. 如图,在平行四边形ABCD中,AD=2,AB,∠B是锐角,AE⊥BC于点E,F是AB的中点,连结DF、EF.若∠EFD=90°,则AE长为( )
A.2 B. C. D.
选:B
10. 如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且
∠ADC=60°,AB=BC,连接OE.下列结论:
①∠CAD=30°;②S ABCD=AB·AC;③OB=AB;④OE=BC,成立的个数有 ( C )
A.1个 B.2个 C.3个 D.4个
选:C.
二、填空题(40分)。
11. 如图,在 ABCD中,过点C作CE⊥AB,垂足为E,若∠EAD=40°,则∠BCE的度数为 .
答案为:50°.
12. 如图, ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则 ABCD的周长等于 .
答案为:16.
13. 在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是
ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小
是 .
答案为:26°
14. 如图,在中,点E在上,且平分,若,,则的面积为________.
【答案】50
15. 如图, ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,使点A正好落在CD上的F点,若△FDE的周长为8cm,△FCB的周长为20cm,则FC的长为________cm.
答案:6
16. 如图,在平行四边形ABCD中,AB=,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为__________.
答案:3
17. 如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD,CB重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是________.
答案:26
18. 如图,在 ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动
点,连接ED并延长至点F,使得DFDE,以EC、EF为邻边构造 EFGC,连接
EG,则EG的最小值为 .
答案为:9.
三、解答题(50分)。
19. 下图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个平行四边形,且另外两个顶点在格点上.请在下面的网格图中画出4种不同的设计图形.
解:如图,四边形ABCD是平行四边形.
20.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延长线于点E,求证:AD=CE.
证明:∵O是CD的中点,
∴OD=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
,
∴△AOD≌△EOC(ASA),
21. 已知 ABCD,O为对角线AC的中点,过O的一条直线交AD于点E,交BC于
点F.
(1)求证:△AOE≌△COF;
(2)若AE:AD=1:2,△AOE的面积为2,求 ABCD的面积.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是AC的中点,
∴OA=OC,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA);
(2)∵AE:AD=1:2,O为对角线AC的中点,
∴AO:AC=1:2,
∵∠EAO=∠DAC,
∵△AOE的面积为2,
∴△ADC的面积为8,
∴平行四边形ABCD的面积为16.
22. 如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为
OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
23. 如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠ADC=∠CBA,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)当BD平分∠ABC时,四边形AFCE是菱形,
理由:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
∴AC⊥EF,
∵DE=BF,
∴OE=OF,
又∵OA=OC,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形.
