九年级数学上册目标测试卷五:第24章 圆 (含答案)
文档属性
| 名称 | 九年级数学上册目标测试卷五:第24章 圆 (含答案) | 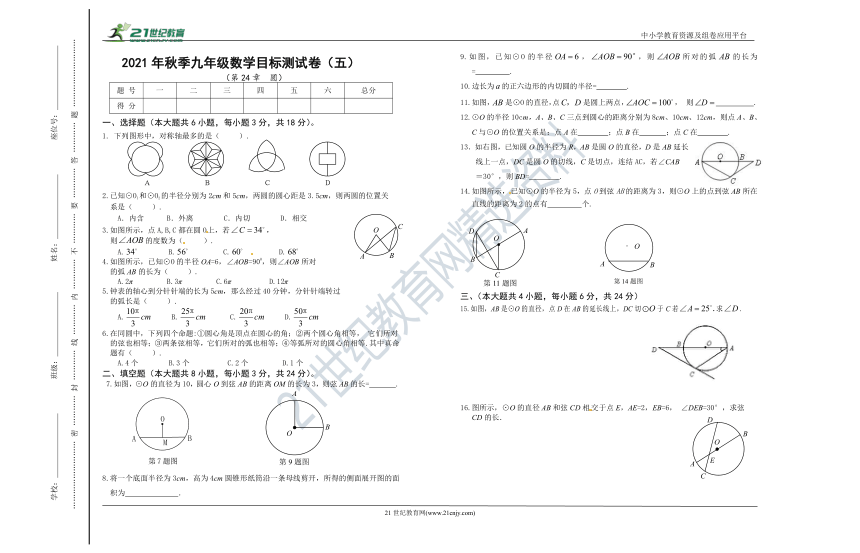 | |
| 格式 | doc | ||
| 文件大小 | 243.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 14:25:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2021年秋季九年级数学目标测试卷(五)
(第24章 圆)
题 号 一 二 三 四 五 六 总分
得 分
一、选择题(本大题共6小题,每小题3分,共18分)。
1. 下列图形中,对称轴最多的是( ).
2.已知⊙O1和⊙O2的半径分别为2cm和5cm,两圆的圆心距是3.5cm,则两圆的位置关
系是( ).
A.内含 B.外离 C.内切 D.相交
3.如图所示,点A,B,C都在圆O上,若,
则的度数为( ).
A. B. C. D.
4.如图所示,已知⊙O的半径OA=6,∠AOB=900,则∠AOB所对
的弧AB的长为( ).
A.2π B.3π C.6π D.12π
5.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过
的弧长是( ).
A. B. C. D.
6.在同圆中,下列四个命题:①圆心角是顶点在圆心的角;②两个圆心角相等, 它们所对
的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中真命题有( ).
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共8小题,每小题3分,共24分)。
7.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长= .
8.将一个底面半径为3cm,高为4cm圆锥形纸筒沿一条母线剪开,所得的侧面展开图的面积为 .
9.如图,已知⊙O的半径,,则所对的弧的长为= .
10.边长为的正六边形的内切圆的半径= .
11.如图,是⊙O的直径,点是圆上两点,, 则 .
⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、
C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
13.如右图,已知圆O的半径为R,AB是圆O的直径,D是AB延长
线上一点,DC是圆O的切线,C是切点,连结AC,若∠CAB
=30°,则BD= .
如图所示,已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上的点到弦AB所在
直线的距离为2的点有 个.
三、(本大题共4小题,每小题6分,共24分)
15.如图,AB是⊙O的直径,点D在AB的延长线上,DC切于C若求.
16.图所示,⊙O的直径AB和弦CD相交于点E,AE=2,EB=6, ∠DEB=30°,求弦
CD的长.
17. 已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,求BC边上的高.
18. 如图,梯形ABCD中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,求圆心O到弦AD的距离.
四、(本大题共3小题,每小题8分,共24分)
如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,求阴影部分的
面积.
21.已知A,B,C,D为圆O上的四点,且=2,问AB与2CD的关系是否相等
五、(本大题共2小题,每小题9分,共18分)
22.如图所示,△ABC内接于⊙O,∠BAC=1200,AB=AC,BD为⊙O的直径,AD=6,求BC
的长.
23.如图,已知AB=AC,∠APC=60°.
求证:△ABC是等边三角形.
若BC=4cm,求⊙O的半径.
六、(本大题共12分)
24.如图所示,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
2021年秋季九年级数学目标测试卷(五)
(第24章 圆 参考答案)
一、选择题:1.B 2.D 3.D 4.B 5.C 6.A
二、填空题: 7.8 8.15πcm2 9. 10. 11.40° 12.圆内;圆上;圆外.
13.. 14.3
三、15.∠D=40°. 16.CD=. 17.BC边上的高为2 .
18圆心O到弦AD的距离为cm.
四、19.⊙O的半径为2. 20.连结OC、OD和CD..
21.解:如图,∵E为的中点,∴==.∴CD=AE=BE.
∵2CD=2AE=2BE=AE+BE,又∵在△AEB中,AB<AE+BE,∴AB<2CD.
五、 22.解:∵ ∠=,∴=.
又∵为直径,∴ ∠=,∴∠=.
∵ ,∴ ,∴//,
∴ 四边形是等腰梯形,∴ .
23.(1)证明:∵∠ABC=∠APC=60°,
又,∴∠ACB=∠ABC=60°,∴△ABC为等边三角形.
(2)解:连结OC,过点O作OD⊥BC,垂足为D,
在Rt△ODC中,DC=2,∠OCD=30°,
设OD=,则OC=2,∴,∴OC=.
六、24.(1)证明:连接. ∵ ,,∴ .
∵ , ∴ .
∴ .
∴ 是的切线.
(2)解: ∵, ∴. ∴ .
在Rt△OCD中, .
∴.
∴ 图中阴影部分的面积为π.
1学校: 班级: 姓名: 座位号: 1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
A
B
C
D
O
C
B
A
O
B
A
第9题图
第7题图
A
O
B
D
C
第11题图
B
A
.
O
第14题图
B
O
A
D
C
E
B
A
C
O
D
A
B
C
.
O
O
D
C
B
A
1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2021年秋季九年级数学目标测试卷(五)
(第24章 圆)
题 号 一 二 三 四 五 六 总分
得 分
一、选择题(本大题共6小题,每小题3分,共18分)。
1. 下列图形中,对称轴最多的是( ).
2.已知⊙O1和⊙O2的半径分别为2cm和5cm,两圆的圆心距是3.5cm,则两圆的位置关
系是( ).
A.内含 B.外离 C.内切 D.相交
3.如图所示,点A,B,C都在圆O上,若,
则的度数为( ).
A. B. C. D.
4.如图所示,已知⊙O的半径OA=6,∠AOB=900,则∠AOB所对
的弧AB的长为( ).
A.2π B.3π C.6π D.12π
5.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过
的弧长是( ).
A. B. C. D.
6.在同圆中,下列四个命题:①圆心角是顶点在圆心的角;②两个圆心角相等, 它们所对
的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中真命题有( ).
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共8小题,每小题3分,共24分)。
7.如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长= .
8.将一个底面半径为3cm,高为4cm圆锥形纸筒沿一条母线剪开,所得的侧面展开图的面积为 .
9.如图,已知⊙O的半径,,则所对的弧的长为= .
10.边长为的正六边形的内切圆的半径= .
11.如图,是⊙O的直径,点是圆上两点,, 则 .
⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、
C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
13.如右图,已知圆O的半径为R,AB是圆O的直径,D是AB延长
线上一点,DC是圆O的切线,C是切点,连结AC,若∠CAB
=30°,则BD= .
如图所示,已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上的点到弦AB所在
直线的距离为2的点有 个.
三、(本大题共4小题,每小题6分,共24分)
15.如图,AB是⊙O的直径,点D在AB的延长线上,DC切于C若求.
16.图所示,⊙O的直径AB和弦CD相交于点E,AE=2,EB=6, ∠DEB=30°,求弦
CD的长.
17. 已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,求BC边上的高.
18. 如图,梯形ABCD中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,求圆心O到弦AD的距离.
四、(本大题共3小题,每小题8分,共24分)
如图,正三角形ABC内接于⊙O,若AB=cm,求⊙O的半径.
如图,半圆的直径AB=10,P为AB上一点,点C,D为半圆的三等分点,求阴影部分的
面积.
21.已知A,B,C,D为圆O上的四点,且=2,问AB与2CD的关系是否相等
五、(本大题共2小题,每小题9分,共18分)
22.如图所示,△ABC内接于⊙O,∠BAC=1200,AB=AC,BD为⊙O的直径,AD=6,求BC
的长.
23.如图,已知AB=AC,∠APC=60°.
求证:△ABC是等边三角形.
若BC=4cm,求⊙O的半径.
六、(本大题共12分)
24.如图所示,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
2021年秋季九年级数学目标测试卷(五)
(第24章 圆 参考答案)
一、选择题:1.B 2.D 3.D 4.B 5.C 6.A
二、填空题: 7.8 8.15πcm2 9. 10. 11.40° 12.圆内;圆上;圆外.
13.. 14.3
三、15.∠D=40°. 16.CD=. 17.BC边上的高为2 .
18圆心O到弦AD的距离为cm.
四、19.⊙O的半径为2. 20.连结OC、OD和CD..
21.解:如图,∵E为的中点,∴==.∴CD=AE=BE.
∵2CD=2AE=2BE=AE+BE,又∵在△AEB中,AB<AE+BE,∴AB<2CD.
五、 22.解:∵ ∠=,∴=.
又∵为直径,∴ ∠=,∴∠=.
∵ ,∴ ,∴//,
∴ 四边形是等腰梯形,∴ .
23.(1)证明:∵∠ABC=∠APC=60°,
又,∴∠ACB=∠ABC=60°,∴△ABC为等边三角形.
(2)解:连结OC,过点O作OD⊥BC,垂足为D,
在Rt△ODC中,DC=2,∠OCD=30°,
设OD=,则OC=2,∴,∴OC=.
六、24.(1)证明:连接. ∵ ,,∴ .
∵ , ∴ .
∴ .
∴ 是的切线.
(2)解: ∵, ∴. ∴ .
在Rt△OCD中, .
∴.
∴ 图中阴影部分的面积为π.
1学校: 班级: 姓名: 座位号: 1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
A
B
C
D
O
C
B
A
O
B
A
第9题图
第7题图
A
O
B
D
C
第11题图
B
A
.
O
第14题图
B
O
A
D
C
E
B
A
C
O
D
A
B
C
.
O
O
D
C
B
A
1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
