2021-2022学年人教版八年级数学下册18.1.2平行四边形的判定 课后提升(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.1.2平行四边形的判定 课后提升(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 405.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 21:21:29 | ||
图片预览



文档简介
平行四边形的判定
一、单选题
1.如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AD∥BC
C.AB∥CD,AD=BC D.AD∥BC,AD=BC
2.如图,平行四边形ABCD中,E、F分别在边BC、AD上,添加条件后不能使AE=CF的是( )
A.BE=DF B.AE∥CF C.AF=AE D.AF=EC
3.在Rt△ABC中,∠B=90°,D,E,F分别是边BC,CA,AB的中点,AB=6,BC=8,则四边形AEDF的周长是( )
A.18 B.16 C.14 D.12
4.如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.∠ABC+∠BCD=180° B.∠ABC=∠ADC
C.AB=CD D.AB=BC
5.如图,点E、F分别是 ABCD边AD、BC的中点,G、H是对角线BD上的两点,且BG=DH.则下列结论中不正确的是( )
A. B.四边形EGFH是平行四边形
C. D.
6.如图,△ABC中,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为点N,∠ACB的平分线垂直AD,垂足为点M,连接MN.若,,则△ABC的周长为( )
A.17 B.18 C.19 D.20
7.如图,在△ABC中,∠ACB=90°,AB=10,以点A为圆心,适当长为半径作弧,交AB于点D,交AC于点E,再以E为圆心,大于DE长为半径作弧,两弧交于点F,在射线AF上取点G,H为BG的中点,连接CH,若AG=6,则CH长为( )
A.1 B.2 C.3 D.4
8.在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( )
A.16 B.24 C.32 D.40
10.如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A. B. C. D.
11.下列图形都是由同样大小的平行四边形按一定的规律组成,其中第①个图形中一共有10个平行四边形,第②个图形中一共有14个平行四边形,第③个图形中一共有19个平行四边形,……按此规律排列下去,则第⑥个图形中平行四边形的个数为( )
A.39 B.40 C.41 D.42
12.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AC=AB,E是AB边的中点,G、F为BC上的点,连接OG和EF,若AB=26,BC=20,GF=10,则图中阴影部分的面积为( )
A.60 B.20 C.120 D.130
二、填空题
13.中,已知AB=CD=4,BC=6,则当AD=________时,四边形ABCD是平行四边形.
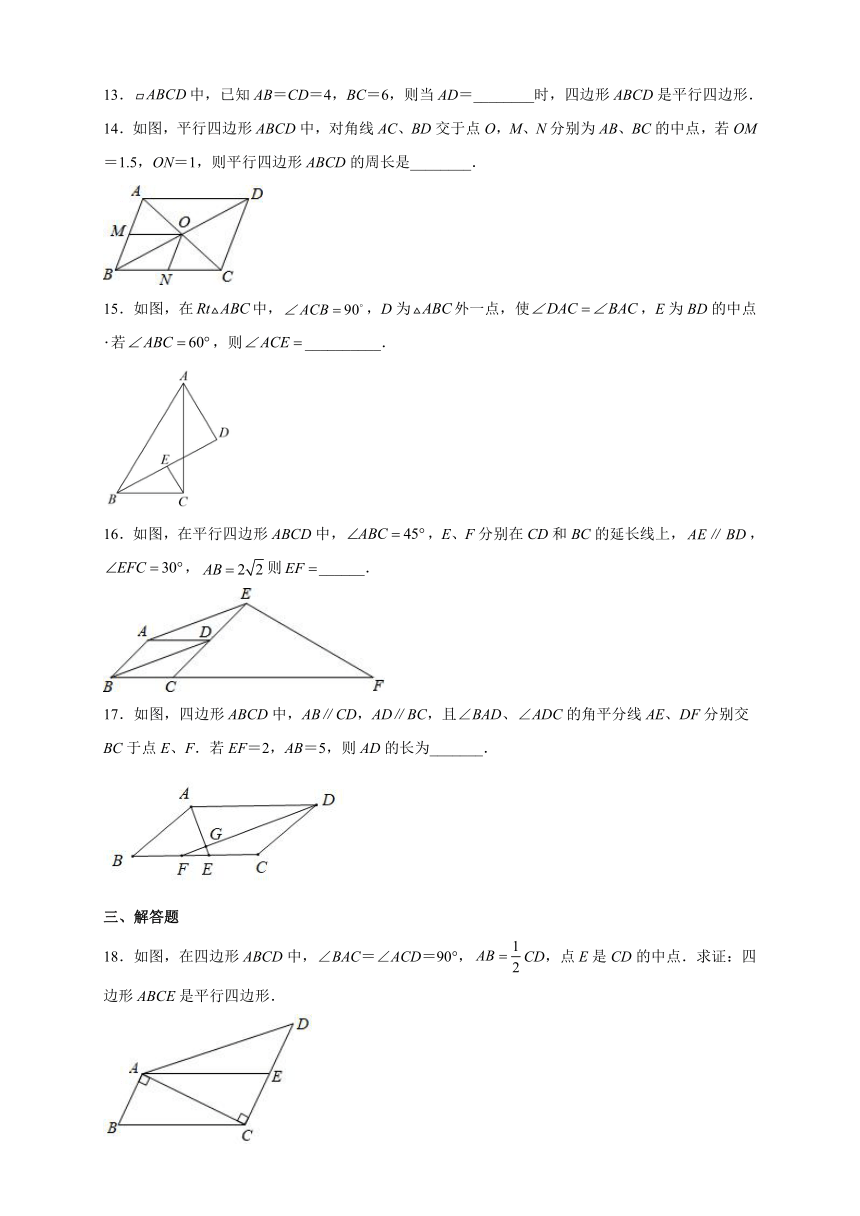
14.如图,平行四边形ABCD中,对角线AC、BD交于点O,M、N分别为AB、BC的中点,若OM=1.5,ON=1,则平行四边形ABCD的周长是________.
15.如图,在中,,D为外一点,使,E为BD的中点若,则__________.
16.如图,在平行四边形ABCD中,,E、F分别在CD和BC的延长线上,,,则______.
17.如图,四边形ABCD中,AB∥CD,AD∥BC,且∠BAD、∠ADC的角平分线AE、DF分别交BC于点E、F.若EF=2,AB=5,则AD的长为_______.
三、解答题
18.如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD,点E是CD的中点.求证:四边形ABCE是平行四边形.
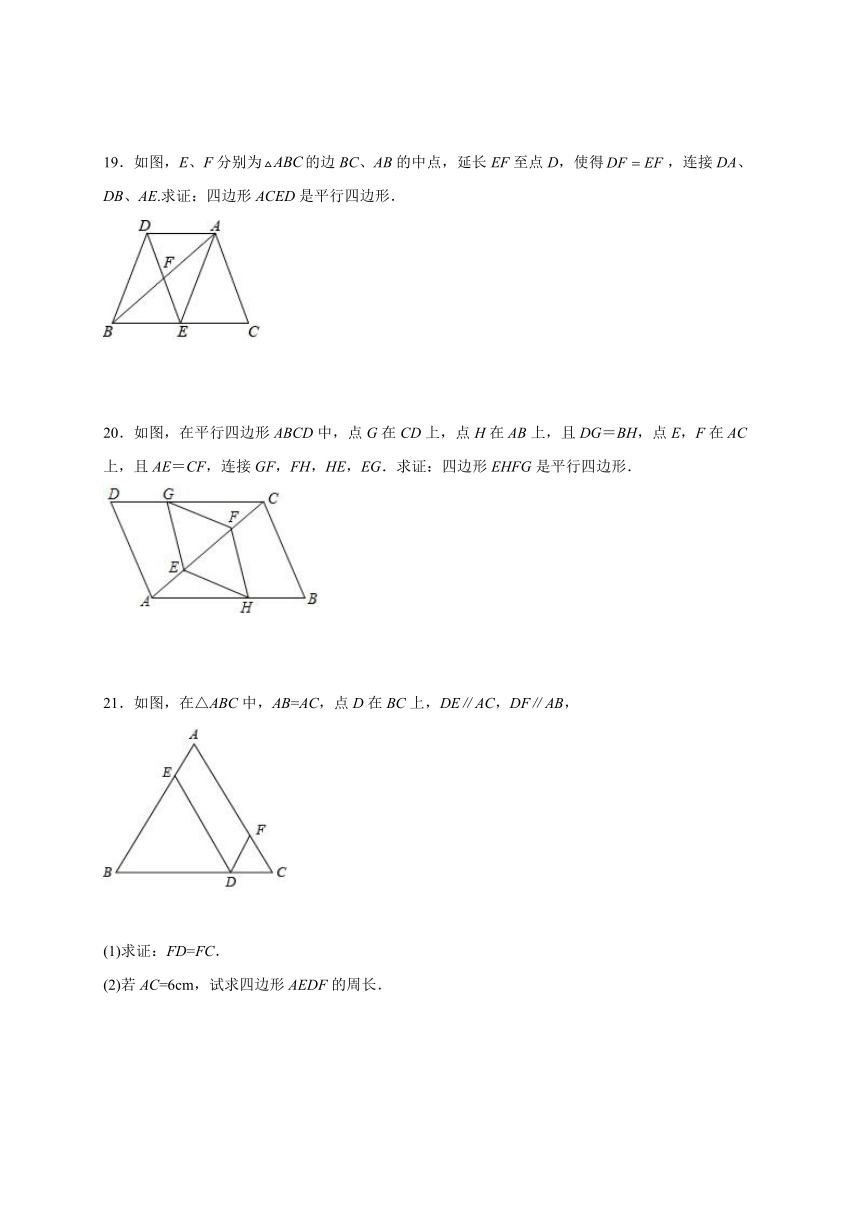
19.如图,E、F分别为的边BC、AB的中点,延长EF至点D,使得,连接DA、DB、AE.求证:四边形ACED是平行四边形.
20.如图,在平行四边形ABCD中,点G在CD上,点H在AB上,且DG=BH,点E,F在AC上,且AE=CF,连接GF,FH,HE,EG.求证:四边形EHFG是平行四边形.
21.如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,DF∥AB,
(1)求证:FD=FC.
(2)若AC=6cm,试求四边形AEDF的周长.
22.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形.
(1)证明:四边形AEFD是平行四边形;
(2)求∠DFE的度数.
23.如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE//AB交AC于点F,CE//AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:A、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
B、根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
C、不能判定四边形ABCD是平行四边形,故此选项符合题意;
D、根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题;
故选:C
2.C
解:A、在 ABCD中,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故A可以使AE=CF,不符合题意;
B、∵AE∥CF,AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故B可以使AE=CF,不符合题意;
C、添加AE=AF后不能使AE=CF,
故C符合题意;
D、∵四边形AECF是平行四边形,
∴AE=CF,
故D可以使AE=CF,不符合题意;
故选C.
3.B
解:略
4.D
解:四边形是用两张对边平行的纸条交叉叠放在一起而组成的图形,
,,
四边形是平行四边形,
,,,故选项、、不符合题意;
而平行四边形中AB和BC不一定相等,故选项符合题意,
故选:.
5.D
解:连接EF交BD于点O,
在平行四边形ABCD中,AD=BC,∠EDH=∠FBG,
∵E、F分别是AD、BC边的中点,
∴DE=BF=BC,∠EDO=∠FBO,∠DOE=∠BOF,
∴△EDO≌△FBO,
∴EO=FO,DO=BO,
∵BG=DH,
∴OH=OG,
∴四边形EGFH是平行四边形,
∴GF=EH,EG=HF,故选项A、B、C正确;
∵∠EHG不一定等于90°,
∴EH⊥BD不正确,故选项D不正确;
故选:D.
6.A
解:∵BN平分∠ABC,
∴∠ABN=∠EBN,
∵BN⊥AE,
∴∠ANB=∠ENB=90°,
在△ABN和△EBN中,,
∴△ABN≌△EBN(ASA),
∴BA=BE,AN=NE,
同理可得:CA=CD,AM=MD,
∵AN=NE,AM=MD,MN=,
∴DE=2MN=3,
∴△ABC的周长=AB+BC+AC=BE+BC+CD=BC+BC+DE=17.
故选:A.
7.B
解:如图,延长交于点
根据作图可知
∠ACB=90°,
在与中
H为BG的中点,
故选B
8.B
解:∵四边形ABCD是平行四边形,
∴,AB=CD,
∵E、F、G分别是OC、OD、AB的中点,
∴CD=2EF,,AB=2BG,
∴BG=EF,,
∴四边形BGFE是平行四边形,
∴GN=NE,故①正确;
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD=BC,
∵BD=2AD=2BC,
∴BO=BC,
又∵点E是OC的中点,
∴BE⊥AC,
∵四边形BGFE是平行四边形,
∴,
∴GF⊥AC,
即GF⊥AE,故②正确;
∵BO=BC,
∴∠BOC=∠BCO,
∵∠BOC=∠ACD+∠BDC,
∴∠BOC>∠ACD,
∴∠BCO≠∠ACD,
∴AC不平分∠BCD,故③错误;
∵BO=BC,点E是OC的中点,
∴BE⊥AC,
∴∠BOE<90°,
∴AC与BD不垂直,故④错误,
故选:B.
9.C
解:∵D,E分别是AB,AC的中点,
∴AE=CE,AD=BD,DE为△ABC的中位线,
∴DE//BC,DE=BC,
∵∠ABC=90°,
∴∠ADE=∠ABC=90°,
在△MBD和△EDA中,,
∴△MBD≌△EDA,
∴MD=AE,DE=MB,
∵DE//MB,
∴四边形DMBE是平行四边形,
∴MD=BE,
∵AC=18,BC=14,
∴四边形DMBE的周长=2DE+2MD=BC+AC=18+14=32.
故选:C.
10.A
解:∵ED=EM,MF=FN,
∴EF=DN,
∴DN最大时,EF最大,
∴N与B重合时DN=DB最大,
在Rt△ADH中, ∵∠A=60°
∴AH=2×=1,DH=,
∴BH=AB﹣AH=3﹣1=2,
∴DB=,
∴EFmax=DB=,
∴EF的最大值为.
故选A
11.B
解:观察图形的变化可知:
第①个图形中一共有10个平行四边形,
第②个图形中一共有14个平行四边形,
第③个图形中一共有19个平行四边形,
第④个图形中一共有25个平行四边形,
第⑤个图形中一共有32个平行四边形,
则第⑥个图形中平行四边形的个数为40.
故选:B.
12.C
解:如图所示,连接EO,EG,OF,
∵平行四边形ABCD中,对角线相交于点O,
∴O是AC的中点,
又∵E是AB边的中点,
∴EO是△ABC的中位线,
∴EO∥BC,EO=BC=10,
又∵GF=10,
∴EO=GF,
∴四边形EOFG是平行四边形,
∴S△EOP+S△FGP=S四边形EOFG=S△EOG,
又∵EO∥BG,
∴S△EOG=S△EOB,
∴S△EOP+S△FGP=S△EOB,
∴S阴影部分=S△AOE+S△EOP+S△FGP=S△AOE+S△EOB=S△ABO,
∵AC=AB=26,BC=20,
∴等腰△ABC中BC边上的高为=24,
∴S△ABC=×20×24=240,
∵O是AC的中点,
∴S△ABO=S△ABC=×240=120,
∴阴影部分的面积为120,
故选C.
13.6
解:略
14.10
解:∵四边形ABCD是平行四边形,
∴BO=DO,AD=BC,AB=CD,
∵M、N分别为AB、BC的中点,
∴MO=AD,NO=CD,
∵OM=1.5,ON=1,
∴AD=3,CD=2,
∴平行四边形ABCD的周长是:3+3+2+2=10,
故答案为:10.
15.##30度
解:延长BC、AD交于F,
在△ABC和△AFC中
,
∴△ABC≌△AFC(ASA),
∴BC=FC,
∴C为BF的中点,
∵E为BD的中点,
∴CE为△BDF的中位线,
∴CE//AF,
∴∠ACE=∠CAF,
∵∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠ACE=∠CAF=∠BAC=30°,
故答案为:30°.
16.8
解:∵四边形ABCD是平行四边形,
∴,AB=CD,
∵,
∴四边形ABDE是平行四边形,
∴DE=CD=,,
过点E作EH⊥BF于H,
∵,
∴∠ECH=,
∴CH=EH,
∵,,
∴CH=EH=4,
∵∠EHF=90°,,
∴EF=2EH=8,
故答案为:8.
17.8
解:∵AD∥BC,
∴∠ADF=∠DFC,
∵DF平分∠ADC,
∴∠ADF=∠CDF,
∴∠DFC=∠CDF,
∴CF=CD,
同理BE=AB,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴AB=BE=CF=CD=5,
∴BC=BE+CF﹣EF=5+5﹣2=8,
∴AD=BC=8,
故答案为:8.
18.证明见解析
解:∵∠BAC=∠ACD=90°,
∴AB∥EC,
∵点E是CD的中点,
∴,
∵,
∴AB=EC,
∴四边形ABCE是平行四边形.
19.见解析
解:∵E、F分别为△ABC的边BC、BA的中点,
∴EFAC,EF=AC,
∵DF=EF,
∴EF=DE,
∴AC=DE,
∴四边形ACED是平行四边形;
20.见解析
解:在平行四边形ABCD中,ABCD,AB=CD,
∴∠GCF=∠HAE,
∵DG=BH,
∴GC=AH,
在△AEH与△CFG中,
,
∴△AEH≌△CFG(SAS),
∴GF=EH,∠AEH=∠GFC,
∴∠FEH=∠EFG,
∴GFEH,
∴四边形EGFH是平行四边形.
21.(1)见解析 (2)四边形AEDF的周长为12cm.
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵DF∥AB,
∴∠FDC=∠B,
∴∠FDC=∠C,
∴FD=FC;
(2)
解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∴C AEDF=AE+ED+DF+AF=2(AF+FD)=2(AF+FC)=2AC=12(cm).
22.(1)见解析 (2)∠DFE=150°.
(1)
证明:∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠FBA=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形;
(2)
解:∵AB=3,AC=4,BC=5,32+42=52,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=360°-60°-90°-60°=150°,
∵四边形AEFD是平行四边形,
∴∠DFE=∠DAE=150°.
23.(1)见解析 (2)成立,理由见解析
(1)
证明:∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,
∵AB∥ED,
∴四边形ABDE是平行四边形;
(2)
解:结论成立,理由如下:
如图,过点M作MG∥DE交CE于G,
∵CE∥AM,
∴四边形DMGE是平行四边形,
∴ED=GM,且ED∥GM,
由(1)知,AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
答案第1页,共2页
一、单选题
1.如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AD∥BC
C.AB∥CD,AD=BC D.AD∥BC,AD=BC
2.如图,平行四边形ABCD中,E、F分别在边BC、AD上,添加条件后不能使AE=CF的是( )
A.BE=DF B.AE∥CF C.AF=AE D.AF=EC
3.在Rt△ABC中,∠B=90°,D,E,F分别是边BC,CA,AB的中点,AB=6,BC=8,则四边形AEDF的周长是( )
A.18 B.16 C.14 D.12
4.如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.∠ABC+∠BCD=180° B.∠ABC=∠ADC
C.AB=CD D.AB=BC
5.如图,点E、F分别是 ABCD边AD、BC的中点,G、H是对角线BD上的两点,且BG=DH.则下列结论中不正确的是( )
A. B.四边形EGFH是平行四边形
C. D.
6.如图,△ABC中,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为点N,∠ACB的平分线垂直AD,垂足为点M,连接MN.若,,则△ABC的周长为( )
A.17 B.18 C.19 D.20
7.如图,在△ABC中,∠ACB=90°,AB=10,以点A为圆心,适当长为半径作弧,交AB于点D,交AC于点E,再以E为圆心,大于DE长为半径作弧,两弧交于点F,在射线AF上取点G,H为BG的中点,连接CH,若AG=6,则CH长为( )
A.1 B.2 C.3 D.4
8.在 ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠ABC=90°,AC=18,BC=14,D,E分别是AB,AC的中点,连接DE,BE,点M在CB的延长线上,连接DM,若∠MDB=∠A,则四边形DMBE的周长为( )
A.16 B.24 C.32 D.40
10.如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A. B. C. D.
11.下列图形都是由同样大小的平行四边形按一定的规律组成,其中第①个图形中一共有10个平行四边形,第②个图形中一共有14个平行四边形,第③个图形中一共有19个平行四边形,……按此规律排列下去,则第⑥个图形中平行四边形的个数为( )
A.39 B.40 C.41 D.42
12.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AC=AB,E是AB边的中点,G、F为BC上的点,连接OG和EF,若AB=26,BC=20,GF=10,则图中阴影部分的面积为( )
A.60 B.20 C.120 D.130
二、填空题
13.中,已知AB=CD=4,BC=6,则当AD=________时,四边形ABCD是平行四边形.
14.如图,平行四边形ABCD中,对角线AC、BD交于点O,M、N分别为AB、BC的中点,若OM=1.5,ON=1,则平行四边形ABCD的周长是________.
15.如图,在中,,D为外一点,使,E为BD的中点若,则__________.
16.如图,在平行四边形ABCD中,,E、F分别在CD和BC的延长线上,,,则______.
17.如图,四边形ABCD中,AB∥CD,AD∥BC,且∠BAD、∠ADC的角平分线AE、DF分别交BC于点E、F.若EF=2,AB=5,则AD的长为_______.
三、解答题
18.如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD,点E是CD的中点.求证:四边形ABCE是平行四边形.
19.如图,E、F分别为的边BC、AB的中点,延长EF至点D,使得,连接DA、DB、AE.求证:四边形ACED是平行四边形.
20.如图,在平行四边形ABCD中,点G在CD上,点H在AB上,且DG=BH,点E,F在AC上,且AE=CF,连接GF,FH,HE,EG.求证:四边形EHFG是平行四边形.
21.如图,在△ABC中,AB=AC,点D在BC上,DE∥AC,DF∥AB,
(1)求证:FD=FC.
(2)若AC=6cm,试求四边形AEDF的周长.
22.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形.
(1)证明:四边形AEFD是平行四边形;
(2)求∠DFE的度数.
23.如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE//AB交AC于点F,CE//AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:A、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
B、根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题意;
C、不能判定四边形ABCD是平行四边形,故此选项符合题意;
D、根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD为平行四边形,故此选项不合题;
故选:C
2.C
解:A、在 ABCD中,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故A可以使AE=CF,不符合题意;
B、∵AE∥CF,AF∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,
故B可以使AE=CF,不符合题意;
C、添加AE=AF后不能使AE=CF,
故C符合题意;
D、∵四边形AECF是平行四边形,
∴AE=CF,
故D可以使AE=CF,不符合题意;
故选C.
3.B
解:略
4.D
解:四边形是用两张对边平行的纸条交叉叠放在一起而组成的图形,
,,
四边形是平行四边形,
,,,故选项、、不符合题意;
而平行四边形中AB和BC不一定相等,故选项符合题意,
故选:.
5.D
解:连接EF交BD于点O,
在平行四边形ABCD中,AD=BC,∠EDH=∠FBG,
∵E、F分别是AD、BC边的中点,
∴DE=BF=BC,∠EDO=∠FBO,∠DOE=∠BOF,
∴△EDO≌△FBO,
∴EO=FO,DO=BO,
∵BG=DH,
∴OH=OG,
∴四边形EGFH是平行四边形,
∴GF=EH,EG=HF,故选项A、B、C正确;
∵∠EHG不一定等于90°,
∴EH⊥BD不正确,故选项D不正确;
故选:D.
6.A
解:∵BN平分∠ABC,
∴∠ABN=∠EBN,
∵BN⊥AE,
∴∠ANB=∠ENB=90°,
在△ABN和△EBN中,,
∴△ABN≌△EBN(ASA),
∴BA=BE,AN=NE,
同理可得:CA=CD,AM=MD,
∵AN=NE,AM=MD,MN=,
∴DE=2MN=3,
∴△ABC的周长=AB+BC+AC=BE+BC+CD=BC+BC+DE=17.
故选:A.
7.B
解:如图,延长交于点
根据作图可知
∠ACB=90°,
在与中
H为BG的中点,
故选B
8.B
解:∵四边形ABCD是平行四边形,
∴,AB=CD,
∵E、F、G分别是OC、OD、AB的中点,
∴CD=2EF,,AB=2BG,
∴BG=EF,,
∴四边形BGFE是平行四边形,
∴GN=NE,故①正确;
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD=BC,
∵BD=2AD=2BC,
∴BO=BC,
又∵点E是OC的中点,
∴BE⊥AC,
∵四边形BGFE是平行四边形,
∴,
∴GF⊥AC,
即GF⊥AE,故②正确;
∵BO=BC,
∴∠BOC=∠BCO,
∵∠BOC=∠ACD+∠BDC,
∴∠BOC>∠ACD,
∴∠BCO≠∠ACD,
∴AC不平分∠BCD,故③错误;
∵BO=BC,点E是OC的中点,
∴BE⊥AC,
∴∠BOE<90°,
∴AC与BD不垂直,故④错误,
故选:B.
9.C
解:∵D,E分别是AB,AC的中点,
∴AE=CE,AD=BD,DE为△ABC的中位线,
∴DE//BC,DE=BC,
∵∠ABC=90°,
∴∠ADE=∠ABC=90°,
在△MBD和△EDA中,,
∴△MBD≌△EDA,
∴MD=AE,DE=MB,
∵DE//MB,
∴四边形DMBE是平行四边形,
∴MD=BE,
∵AC=18,BC=14,
∴四边形DMBE的周长=2DE+2MD=BC+AC=18+14=32.
故选:C.
10.A
解:∵ED=EM,MF=FN,
∴EF=DN,
∴DN最大时,EF最大,
∴N与B重合时DN=DB最大,
在Rt△ADH中, ∵∠A=60°
∴AH=2×=1,DH=,
∴BH=AB﹣AH=3﹣1=2,
∴DB=,
∴EFmax=DB=,
∴EF的最大值为.
故选A
11.B
解:观察图形的变化可知:
第①个图形中一共有10个平行四边形,
第②个图形中一共有14个平行四边形,
第③个图形中一共有19个平行四边形,
第④个图形中一共有25个平行四边形,
第⑤个图形中一共有32个平行四边形,
则第⑥个图形中平行四边形的个数为40.
故选:B.
12.C
解:如图所示,连接EO,EG,OF,
∵平行四边形ABCD中,对角线相交于点O,
∴O是AC的中点,
又∵E是AB边的中点,
∴EO是△ABC的中位线,
∴EO∥BC,EO=BC=10,
又∵GF=10,
∴EO=GF,
∴四边形EOFG是平行四边形,
∴S△EOP+S△FGP=S四边形EOFG=S△EOG,
又∵EO∥BG,
∴S△EOG=S△EOB,
∴S△EOP+S△FGP=S△EOB,
∴S阴影部分=S△AOE+S△EOP+S△FGP=S△AOE+S△EOB=S△ABO,
∵AC=AB=26,BC=20,
∴等腰△ABC中BC边上的高为=24,
∴S△ABC=×20×24=240,
∵O是AC的中点,
∴S△ABO=S△ABC=×240=120,
∴阴影部分的面积为120,
故选C.
13.6
解:略
14.10
解:∵四边形ABCD是平行四边形,
∴BO=DO,AD=BC,AB=CD,
∵M、N分别为AB、BC的中点,
∴MO=AD,NO=CD,
∵OM=1.5,ON=1,
∴AD=3,CD=2,
∴平行四边形ABCD的周长是:3+3+2+2=10,
故答案为:10.
15.##30度
解:延长BC、AD交于F,
在△ABC和△AFC中
,
∴△ABC≌△AFC(ASA),
∴BC=FC,
∴C为BF的中点,
∵E为BD的中点,
∴CE为△BDF的中位线,
∴CE//AF,
∴∠ACE=∠CAF,
∵∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠ACE=∠CAF=∠BAC=30°,
故答案为:30°.
16.8
解:∵四边形ABCD是平行四边形,
∴,AB=CD,
∵,
∴四边形ABDE是平行四边形,
∴DE=CD=,,
过点E作EH⊥BF于H,
∵,
∴∠ECH=,
∴CH=EH,
∵,,
∴CH=EH=4,
∵∠EHF=90°,,
∴EF=2EH=8,
故答案为:8.
17.8
解:∵AD∥BC,
∴∠ADF=∠DFC,
∵DF平分∠ADC,
∴∠ADF=∠CDF,
∴∠DFC=∠CDF,
∴CF=CD,
同理BE=AB,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴AB=BE=CF=CD=5,
∴BC=BE+CF﹣EF=5+5﹣2=8,
∴AD=BC=8,
故答案为:8.
18.证明见解析
解:∵∠BAC=∠ACD=90°,
∴AB∥EC,
∵点E是CD的中点,
∴,
∵,
∴AB=EC,
∴四边形ABCE是平行四边形.
19.见解析
解:∵E、F分别为△ABC的边BC、BA的中点,
∴EFAC,EF=AC,
∵DF=EF,
∴EF=DE,
∴AC=DE,
∴四边形ACED是平行四边形;
20.见解析
解:在平行四边形ABCD中,ABCD,AB=CD,
∴∠GCF=∠HAE,
∵DG=BH,
∴GC=AH,
在△AEH与△CFG中,
,
∴△AEH≌△CFG(SAS),
∴GF=EH,∠AEH=∠GFC,
∴∠FEH=∠EFG,
∴GFEH,
∴四边形EGFH是平行四边形.
21.(1)见解析 (2)四边形AEDF的周长为12cm.
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵DF∥AB,
∴∠FDC=∠B,
∴∠FDC=∠C,
∴FD=FC;
(2)
解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∴C AEDF=AE+ED+DF+AF=2(AF+FD)=2(AF+FC)=2AC=12(cm).
22.(1)见解析 (2)∠DFE=150°.
(1)
证明:∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠FBA=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,
,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形;
(2)
解:∵AB=3,AC=4,BC=5,32+42=52,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=360°-60°-90°-60°=150°,
∵四边形AEFD是平行四边形,
∴∠DFE=∠DAE=150°.
23.(1)见解析 (2)成立,理由见解析
(1)
证明:∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,
∵AB∥ED,
∴四边形ABDE是平行四边形;
(2)
解:结论成立,理由如下:
如图,过点M作MG∥DE交CE于G,
∵CE∥AM,
∴四边形DMGE是平行四边形,
∴ED=GM,且ED∥GM,
由(1)知,AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
答案第1页,共2页
