4.3.2 探索三角形全等的条件同步课时作业(含答案)
文档属性
| 名称 | 4.3.2 探索三角形全等的条件同步课时作业(含答案) | 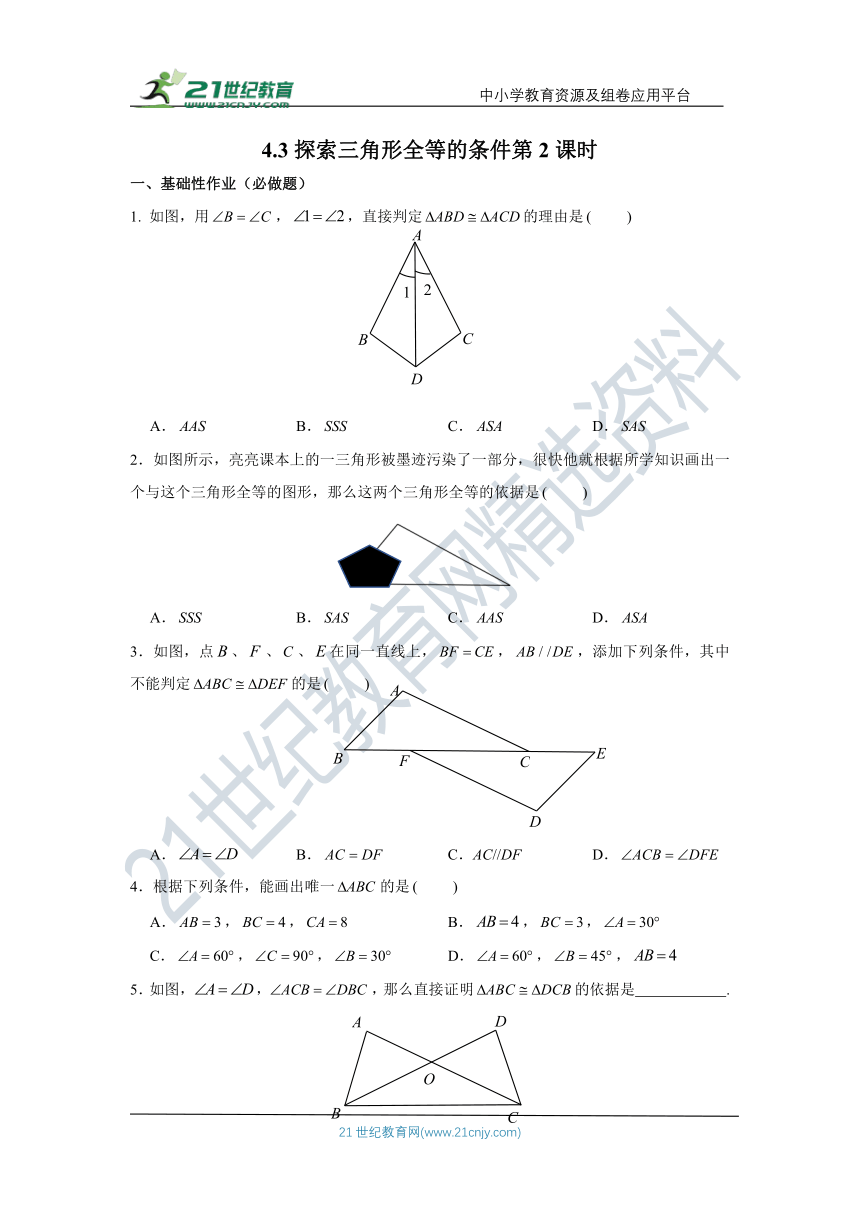 | |
| 格式 | docx | ||
| 文件大小 | 361.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 19:23:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.3探索三角形全等的条件第2课时
一、基础性作业(必做题)
1. 如图,用,,直接判定的理由是
A. B. C. D.
2.如图所示,亮亮课本上的一三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与这个三角形全等的图形,那么这两个三角形全等的依据是
A. B. C. D.
3.如图,点、、、在同一直线上,,,添加下列条件,其中不能判定的是
A. B. C.AC//DF D.
4.根据下列条件,能画出唯一的是
A.,, B.,,
C.,, D.,,
5.如图,,,那么直接证明的依据是 .
6. 如图,AD=AE,∠B=∠C,∠BEC=55°,求∠ADC的度数.
7. 填补下列证明过程.
如图,点,在线段上,,,.
求证:.
证明:
(已知)
.
在和中
.
二、拓展性作业(选做题)
1. 如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6,则BD的长为( )
A.1 B.2 C.2.5 D.3
2.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,连结BF,CE,若BF∥CE.则下列说法:①CE=BF;②△ACE与△CDE的面积相等;③DE=DF;④△ACE与△BDF的面积之和等于△ABD的面积.其中正确的是________(请填序号)
A.②③④ B.①③④ C.①②④ D.①②③
2. 如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,
请说明:
①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,判断△ADC和△CEB的关系,并说明理由.
4.3探索三角形全等的条件第2课时参考答案
一、基础性作业(必做题)
1.A.
2.D.
3.B.
4.D.
5..
6.解:在和中
7.解:(已知)
两直线平行,内错角相等.
在和中
ASA.
二、拓展性作业(选做题)
1.D.
2.①③④.
3.(1)①证明:∵∠ACB=90°,∠ADC=90°,∠BEC=90°
∴∠ACD+∠DAC=90°,∠ACD+∠BCE=90°.
∴∠DAC=∠BCE.
在△ADC与△CEB中,
,
∴△ADC≌△CEB(AAS);
②证明:由①知,△ADC≌△BEC,
∴AD=CE,BE=CD,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:结论:△ADC≌△CEB.
理由:∵AD⊥MN于D,BE⊥MN于E.
∴∠ADC=∠BEC=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°.
∴∠CAD=∠BCE.
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS).
21世纪教育网(www.21cnjy.com)
4.3探索三角形全等的条件第2课时
一、基础性作业(必做题)
1. 如图,用,,直接判定的理由是
A. B. C. D.
2.如图所示,亮亮课本上的一三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与这个三角形全等的图形,那么这两个三角形全等的依据是
A. B. C. D.
3.如图,点、、、在同一直线上,,,添加下列条件,其中不能判定的是
A. B. C.AC//DF D.
4.根据下列条件,能画出唯一的是
A.,, B.,,
C.,, D.,,
5.如图,,,那么直接证明的依据是 .
6. 如图,AD=AE,∠B=∠C,∠BEC=55°,求∠ADC的度数.
7. 填补下列证明过程.
如图,点,在线段上,,,.
求证:.
证明:
(已知)
.
在和中
.
二、拓展性作业(选做题)
1. 如图,E是△ABC的边AC的中点,过点C作CF∥AB,过点E作直线DF交AB于D,交CF于F,若AB=9,CF=6,则BD的长为( )
A.1 B.2 C.2.5 D.3
2.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,连结BF,CE,若BF∥CE.则下列说法:①CE=BF;②△ACE与△CDE的面积相等;③DE=DF;④△ACE与△BDF的面积之和等于△ABD的面积.其中正确的是________(请填序号)
A.②③④ B.①③④ C.①②④ D.①②③
2. 如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,
请说明:
①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,判断△ADC和△CEB的关系,并说明理由.
4.3探索三角形全等的条件第2课时参考答案
一、基础性作业(必做题)
1.A.
2.D.
3.B.
4.D.
5..
6.解:在和中
7.解:(已知)
两直线平行,内错角相等.
在和中
ASA.
二、拓展性作业(选做题)
1.D.
2.①③④.
3.(1)①证明:∵∠ACB=90°,∠ADC=90°,∠BEC=90°
∴∠ACD+∠DAC=90°,∠ACD+∠BCE=90°.
∴∠DAC=∠BCE.
在△ADC与△CEB中,
,
∴△ADC≌△CEB(AAS);
②证明:由①知,△ADC≌△BEC,
∴AD=CE,BE=CD,
∵DE=CE+CD,
∴DE=AD+BE;
(2)解:结论:△ADC≌△CEB.
理由:∵AD⊥MN于D,BE⊥MN于E.
∴∠ADC=∠BEC=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°.
∴∠CAD=∠BCE.
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS).
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
