华师版数学七年级下册同步课时练习:第6章一元一次方程 单元复习小结(word,有答案)
文档属性
| 名称 | 华师版数学七年级下册同步课时练习:第6章一元一次方程 单元复习小结(word,有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-01 00:00:00 | ||
图片预览


文档简介
单元复习小结
类型之一 认识一元一次方程
1.下列方程中是一元一次方程的是 ( )
A.1-=3y-2 B.-2=y
C.3x+1=2x D.3x2+1=0
2.(2021重庆)若关于x的方程+a=4的解是x=2,则a的值为 .
3.若-2x2+3m+1=0是关于x的一元一次方程,则m= ,x= .
类型之二 一元一次方程的解法
4.下列方程变形中,正确的是 ( )
A.方程5x-2=2x+1,移项,得5x-2x=-1+2
B.方程3-x=2-5(x-1),去括号,得3-x=2-5x+1
C.方程x=,系数化为1,得x=1
D.方程=,去分母,得x+1=3x-1
5.解下列方程:
(1)4x-2=3-x; (2)5(x-5)+2x=-4;
(3)=-1; (4)-=1.
类型之三 一元一次方程的应用
6.(2021武汉)我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何.”意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问人数、物价各是多少.若设共有x人,物价是y钱,则下列方程正确的是 ( )
A.8(x-3)=7(x+4) B.8x+3=7x-4
C.= D.=
7.(2020攀枝花)课外活动中一些学生分组参加活动,原来每组6人,后来重新编组,每组8人,这样就比原来减少2组,则这些学生共有多少人
8.甲、乙两人从A地出发前往B地,甲出发2 h后乙才出发,已知甲的速度是15 km/h,乙的速度是60 km/h,A,B两地相距100 km,乙追上甲的地方离B地多远
9.某工程队承包了某段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲班组比乙班组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.
(1)求甲、乙两个班组平均每天各掘进多少米;
(2)为加快进度,通过改进施工技术,在剩余的工程中,甲班组平均每天能比原来多掘进0.2米,乙班组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务
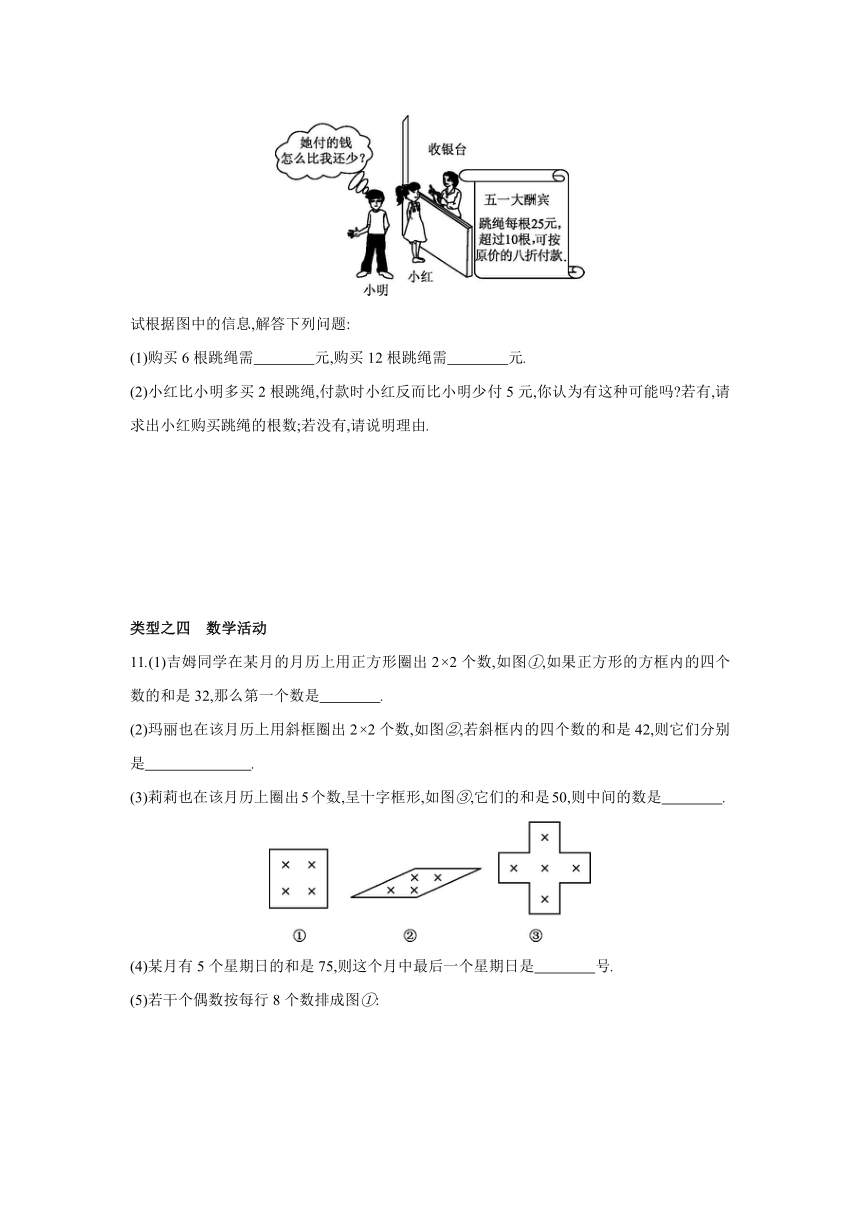
10.情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需 元,购买12根跳绳需 元.
(2)小红比小明多买2根跳绳,付款时小红反而比小明少付5元,你认为有这种可能吗 若有,请求出小红购买跳绳的根数;若没有,请说明理由.
类型之四 数学活动
11.(1)吉姆同学在某月的月历上用正方形圈出2×2个数,如图①,如果正方形的方框内的四个数的和是32,那么第一个数是 .
(2)玛丽也在该月历上用斜框圈出2×2个数,如图②,若斜框内的四个数的和是42,则它们分别是 .
(3)莉莉也在该月历上圈出5个数,呈十字框形,如图③,它们的和是50,则中间的数是 .
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号.
(5)若干个偶数按每行8个数排成图①:
①图①中方框内的9个数的和与中间的数有什么关系 ;
②汤姆所画的如图②所示的斜框内9个数的和为360,则斜框的中间一个数是 ;
③托马斯也画了一个如图②所示的斜框,斜框内9个数的和为252,则斜框的中间一个数是 .
小结
1.C
2.3 把x=2代入方程+a=4,
得+a=4,解得a=3.
故答案为3.
3.-
4.D 方程5x-2=2x+1,移项,得5x-2x=1+2,故A错误;
方程3-x=2-5(x-1),去括号,得3-x=2-5x+5,故B错误;
方程x=,系数化为1,得x=,故C错误;
方程=,去分母,得x+1=3x-1,故D正确.
故选D.
5.解:(1)移项,得4x+x=3+2.
合并同类项,得5x=5.
系数化为1,得x=1.
(2)去括号,得5x-25+2x=-4.
移项、合并同类项,得7x=21.
系数化为1,得x=3.
(3)去分母,得4(2x-1)=3(x+2)-12.
去括号,得8x-4=3x+6-12.
移项、合并同类项,得5x=-2.
系数化为1,得x=-.
(4)去分母,得2(2x+1)-(5x-1)=6.
去括号,得4x+2-5x+1=6.
移项、合并同类项,得-x=3.
系数化为1,得x=-3.
6.D
7.解:设这些学生共有x人.
根据题意,得-=2,解得x=48.
答:这些学生共有48人.
8.解:设乙出发x h后追上甲,则此时甲行了(x+2)h.
根据题意,得60x=15(x+2),
解得x=,
所以100-60x=100-60×=60(km).
答:乙追上甲的地方离B地60 km.
9.解:(1)设乙班组平均每天掘进x米,则甲班组平均每天掘进(x+0.6)米.
根据题意,得5x+5(x+0.6)=45.
解此方程,得x=4.2.
则x+0.6=4.8.
答:甲班组平均每天掘进4.8米,乙班组平均每天掘进4.2米.
(2)改进施工技术后,甲班组平均每天掘进4.8+0.2=5(米),乙班组平均每天掘进4.2+0.3=4.5(米).
改进施工技术后,剩余的工程所用时间为(1755-45)÷(5+4.5)=180(天).
按原来速度,剩余的工程所用时间为(1755-45)÷(4.8+4.2)=190(天).
少用天数为190-180=10(天).
答:按此施工进度,能够比原来少用10天完成任务.
10.解:(1)25×6=150(元),
25×12×0.8=240(元).
即购买6根跳绳需150元,购买12根跳绳需240元.
故答案为150,240.
(2)有这种可能.
设小红购买了x根跳绳.
根据题意,得25×0.8x=25(x-2)-5,
解得x=11.
故小红购买了11根跳绳.
11.(1)4 (2)7,8,13,14 (3)10 (4)29
(5)①9个数的和是中间的数的9倍 ②40 ③28
(1)设第一个数是x,则其他的数分别为x+1,x+7,x+8,
则x+x+1+x+7+x+8=32,解得x=4.
即第一个数是4.故答案为4.
(2)设第一个数是y,则其他的数分别为y+1,y+6,y+7,
则y+y+1+y+6+y+7=42,解得y=7.
y+1=8,y+6=13,y+7=14.
故答案为7,8,13,14.
(3)设中间的数是z,则5z=50,解得z=10.
故答案为10.
(4)设最后一个星期日是m号,
则m+m-7+m-14+m-21+m-28=75,解得m=29.故答案为29.
(5)①9个数的和是中间的数的9倍.
②根据规律可知,和是中间的数的9倍,设斜框的中间一个数是n,
则9n=360,解得n=40.故答案为40.
③设斜框的中间一个数是p,则9p=252,解得p=28.故答案为28.
类型之一 认识一元一次方程
1.下列方程中是一元一次方程的是 ( )
A.1-=3y-2 B.-2=y
C.3x+1=2x D.3x2+1=0
2.(2021重庆)若关于x的方程+a=4的解是x=2,则a的值为 .
3.若-2x2+3m+1=0是关于x的一元一次方程,则m= ,x= .
类型之二 一元一次方程的解法
4.下列方程变形中,正确的是 ( )
A.方程5x-2=2x+1,移项,得5x-2x=-1+2
B.方程3-x=2-5(x-1),去括号,得3-x=2-5x+1
C.方程x=,系数化为1,得x=1
D.方程=,去分母,得x+1=3x-1
5.解下列方程:
(1)4x-2=3-x; (2)5(x-5)+2x=-4;
(3)=-1; (4)-=1.
类型之三 一元一次方程的应用
6.(2021武汉)我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何.”意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问人数、物价各是多少.若设共有x人,物价是y钱,则下列方程正确的是 ( )
A.8(x-3)=7(x+4) B.8x+3=7x-4
C.= D.=
7.(2020攀枝花)课外活动中一些学生分组参加活动,原来每组6人,后来重新编组,每组8人,这样就比原来减少2组,则这些学生共有多少人
8.甲、乙两人从A地出发前往B地,甲出发2 h后乙才出发,已知甲的速度是15 km/h,乙的速度是60 km/h,A,B两地相距100 km,乙追上甲的地方离B地多远
9.某工程队承包了某段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲班组比乙班组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.
(1)求甲、乙两个班组平均每天各掘进多少米;
(2)为加快进度,通过改进施工技术,在剩余的工程中,甲班组平均每天能比原来多掘进0.2米,乙班组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务
10.情景:
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需 元,购买12根跳绳需 元.
(2)小红比小明多买2根跳绳,付款时小红反而比小明少付5元,你认为有这种可能吗 若有,请求出小红购买跳绳的根数;若没有,请说明理由.
类型之四 数学活动
11.(1)吉姆同学在某月的月历上用正方形圈出2×2个数,如图①,如果正方形的方框内的四个数的和是32,那么第一个数是 .
(2)玛丽也在该月历上用斜框圈出2×2个数,如图②,若斜框内的四个数的和是42,则它们分别是 .
(3)莉莉也在该月历上圈出5个数,呈十字框形,如图③,它们的和是50,则中间的数是 .
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号.
(5)若干个偶数按每行8个数排成图①:
①图①中方框内的9个数的和与中间的数有什么关系 ;
②汤姆所画的如图②所示的斜框内9个数的和为360,则斜框的中间一个数是 ;
③托马斯也画了一个如图②所示的斜框,斜框内9个数的和为252,则斜框的中间一个数是 .
小结
1.C
2.3 把x=2代入方程+a=4,
得+a=4,解得a=3.
故答案为3.
3.-
4.D 方程5x-2=2x+1,移项,得5x-2x=1+2,故A错误;
方程3-x=2-5(x-1),去括号,得3-x=2-5x+5,故B错误;
方程x=,系数化为1,得x=,故C错误;
方程=,去分母,得x+1=3x-1,故D正确.
故选D.
5.解:(1)移项,得4x+x=3+2.
合并同类项,得5x=5.
系数化为1,得x=1.
(2)去括号,得5x-25+2x=-4.
移项、合并同类项,得7x=21.
系数化为1,得x=3.
(3)去分母,得4(2x-1)=3(x+2)-12.
去括号,得8x-4=3x+6-12.
移项、合并同类项,得5x=-2.
系数化为1,得x=-.
(4)去分母,得2(2x+1)-(5x-1)=6.
去括号,得4x+2-5x+1=6.
移项、合并同类项,得-x=3.
系数化为1,得x=-3.
6.D
7.解:设这些学生共有x人.
根据题意,得-=2,解得x=48.
答:这些学生共有48人.
8.解:设乙出发x h后追上甲,则此时甲行了(x+2)h.
根据题意,得60x=15(x+2),
解得x=,
所以100-60x=100-60×=60(km).
答:乙追上甲的地方离B地60 km.
9.解:(1)设乙班组平均每天掘进x米,则甲班组平均每天掘进(x+0.6)米.
根据题意,得5x+5(x+0.6)=45.
解此方程,得x=4.2.
则x+0.6=4.8.
答:甲班组平均每天掘进4.8米,乙班组平均每天掘进4.2米.
(2)改进施工技术后,甲班组平均每天掘进4.8+0.2=5(米),乙班组平均每天掘进4.2+0.3=4.5(米).
改进施工技术后,剩余的工程所用时间为(1755-45)÷(5+4.5)=180(天).
按原来速度,剩余的工程所用时间为(1755-45)÷(4.8+4.2)=190(天).
少用天数为190-180=10(天).
答:按此施工进度,能够比原来少用10天完成任务.
10.解:(1)25×6=150(元),
25×12×0.8=240(元).
即购买6根跳绳需150元,购买12根跳绳需240元.
故答案为150,240.
(2)有这种可能.
设小红购买了x根跳绳.
根据题意,得25×0.8x=25(x-2)-5,
解得x=11.
故小红购买了11根跳绳.
11.(1)4 (2)7,8,13,14 (3)10 (4)29
(5)①9个数的和是中间的数的9倍 ②40 ③28
(1)设第一个数是x,则其他的数分别为x+1,x+7,x+8,
则x+x+1+x+7+x+8=32,解得x=4.
即第一个数是4.故答案为4.
(2)设第一个数是y,则其他的数分别为y+1,y+6,y+7,
则y+y+1+y+6+y+7=42,解得y=7.
y+1=8,y+6=13,y+7=14.
故答案为7,8,13,14.
(3)设中间的数是z,则5z=50,解得z=10.
故答案为10.
(4)设最后一个星期日是m号,
则m+m-7+m-14+m-21+m-28=75,解得m=29.故答案为29.
(5)①9个数的和是中间的数的9倍.
②根据规律可知,和是中间的数的9倍,设斜框的中间一个数是n,
则9n=360,解得n=40.故答案为40.
③设斜框的中间一个数是p,则9p=252,解得p=28.故答案为28.
