人教版八年级数学下册第 18章平行四边形 综合练习 (word版含答案)
文档属性
| 名称 | 人教版八年级数学下册第 18章平行四边形 综合练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 344.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 07:06:36 | ||
图片预览



文档简介
2021-2022学年人教版八年级数学下册
第18章《平行四边形》综合练习
一、单选题
1.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(7,3) B.(8,2) C.(3,7) D.(5,3)
2.如图,四边形中,R、P分别是上的点,E、F分别是的中点,当点P在上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段的长逐渐增大 B.线段的长逐渐减小
C.线段的长不变 D.线段的长与点P的位置有关
3.点A、B、C、D在同一平面内,从(1),(2),(3),(4)这四个条件中任选两个,能使四边形是平行四边形的选法有( )种.
A.3 B.4 C.5 D.6
4.如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
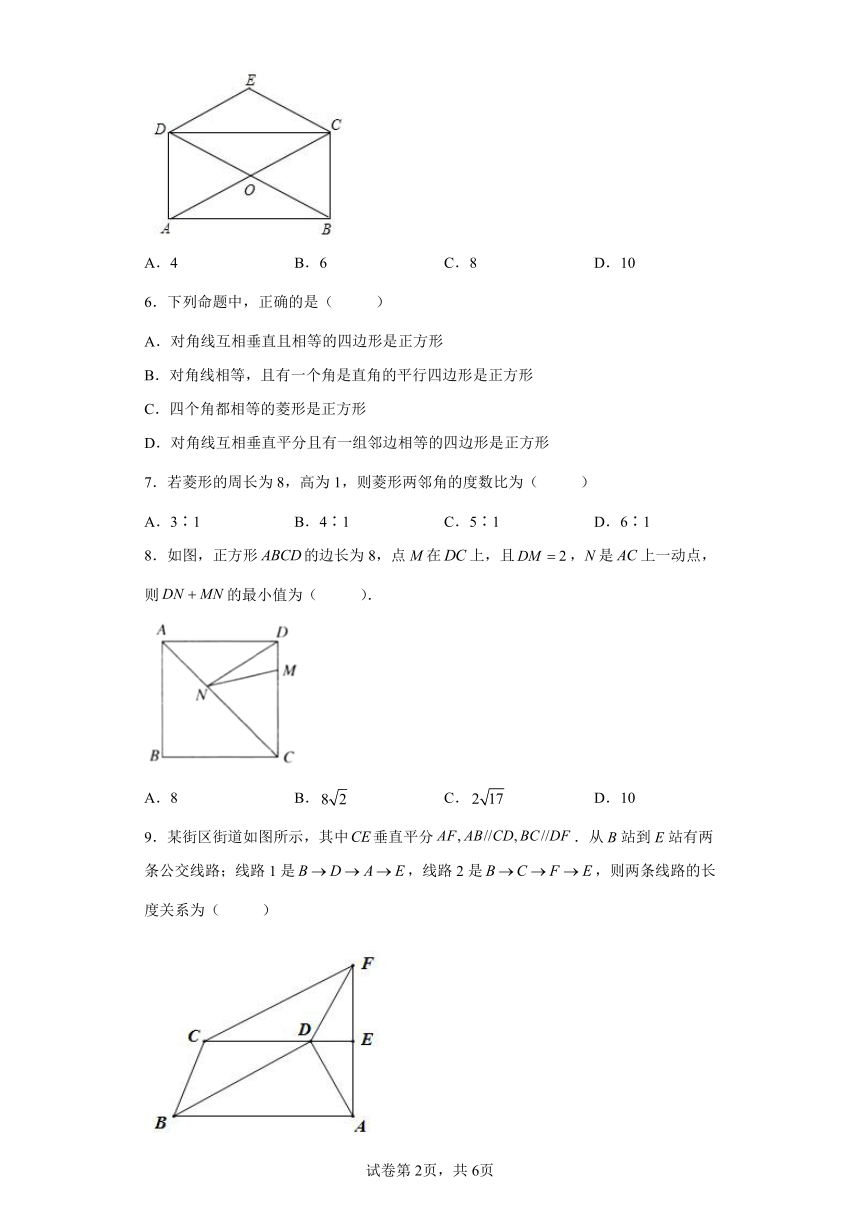
5.如图,矩形的对角线,相交于点O,.若,则四边形的周长为( ).
A.4 B.6 C.8 D.10
6.下列命题中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线相等,且有一个角是直角的平行四边形是正方形
C.四个角都相等的菱形是正方形
D.对角线互相垂直平分且有一组邻边相等的四边形是正方形
7.若菱形的周长为8,高为1,则菱形两邻角的度数比为( )
A.3∶1 B.4∶1 C.5∶1 D.6∶1
8.如图,正方形的边长为8,点M在上,且,N是上一动点,则的最小值为( ).
A.8 B. C. D.10
9.某街区街道如图所示,其中垂直平分.从B站到E站有两条公交线路;线路1是,线路2是,则两条线路的长度关系为( )
A.路线1较短 B.路线2较短
C.两条路线长度相等 D.两条线路长度不确定
10.在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为( )
A. B. C.或 D.或
二、填空题
11.如图,中,,则的长为_________.
12.在中,已知对角线交于点O,的周长为17,,那么对角线_________.
13.如图,在中,,于E,则_______.
14.过对角线交点O作直线m,分别交直线于点E,交直线于点F,若,则的长是_________.
15.如图,在四边形中,,且,点P,Q分别从A,C两点同时出发,点P以的速度由A向D运动,点Q以的速度由向C运动B,则_____秒后四边形成为一个平行四边形.
三、解答题
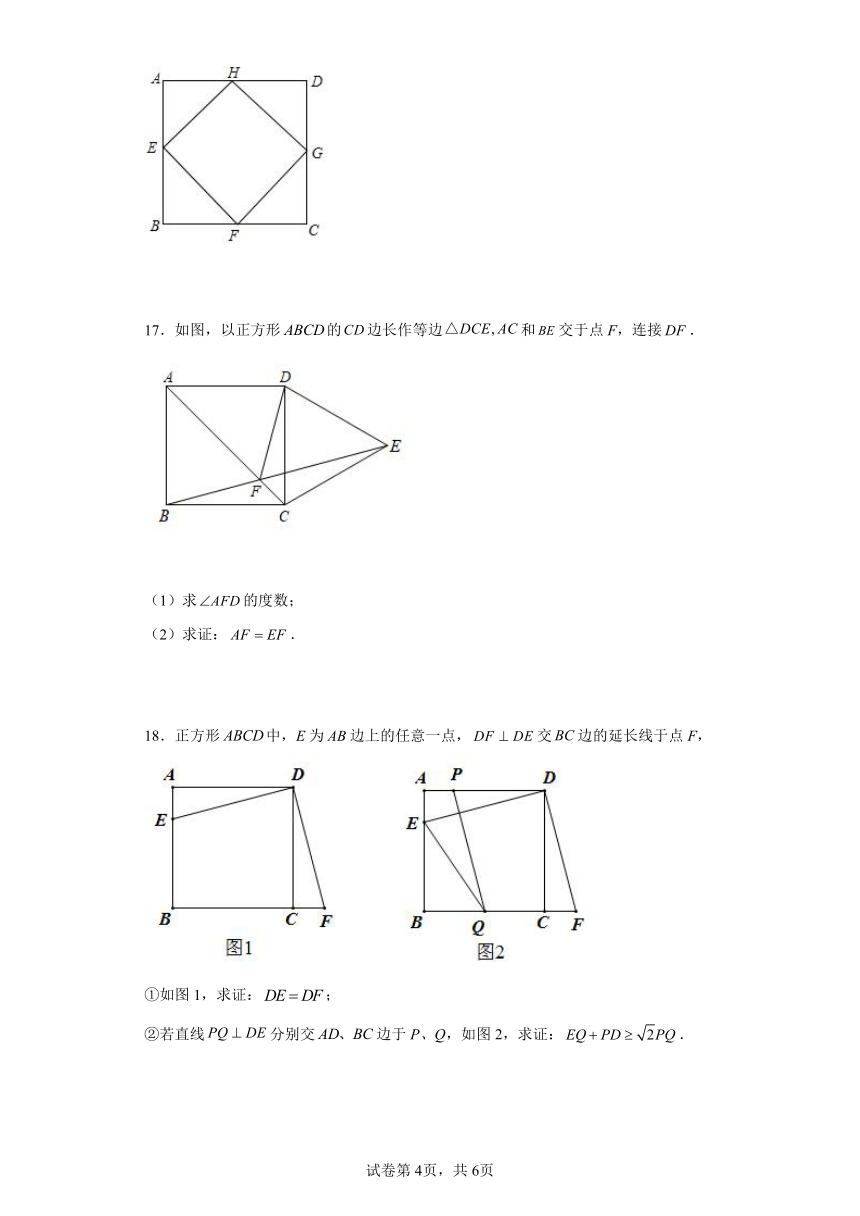
16.如图,,,,分别是正方形各边的中点.四边形是什么四边形?为什么?
17.如图,以正方形的边长作等边和交于点F,连接.
(1)求的度数;
(2)求证:.
18.正方形中,E为边上的任意一点,交边的延长线于点F,
①如图1,求证:;
②若直线分别交边于P、Q,如图2,求证:.
19.如图,在 中,,过点 的直线MN//AB,为 边上一点,过点 作 ,垂足为点 ,交直线 于点 ,连接 ,.
(1)求证:;
(2)当 为 中点时,四边形 是什么特殊四边形 说明你的理由;
(3)在()的条件下,当 的大小满足什么条件时,四边形 是正方形 请说明你的理由.
20.已知:如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别相交于点E、F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?并给出证明.
21.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
22.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
23.如图,已知以△ABC的三边为边在BC的同侧作等边△ABD,△BCE,△ACF,请回答下列问题:
(1)四边形ADEF是什么四边形?请说明理由.
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.C
3.B
4.A
5.C
6.C
7.C
8.D
9.C
10.C
11.
12.22
13.
14.10或2
15.2
16.
解:四边形是正方形,理由如下:
连接AC、BD.
∵E、F、G、H分别是正方形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=BD,EF=HG=AC,
∴四边形EFGH为平行四边形,
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴EF=FG,EF⊥FG,
∴ EFGH是正方形.
17.
(1)∵四边形ABCD是正方形
∴AD=CD=BC,∠ADC=∠BCD=90°,∠DAC=∠BCF=∠DCF=45°
∵△DCE是等边三角形
∴CD=CE=DE,∠EDC=∠ECD=60°
∴BC=CE=AD=DE,∠BCE=∠BCD+∠ECD=150°
∴△BCE是等腰三角形
∴∠CBF=∠CEB=
在△CDF与△CBF中
∴△CBF≌△CDF(SAS)
∴∠CDF=∠CBF=15°
∴∠ADF=90°-∠CDF=75°
在△ADF中,∠AFD=180°-∠ADF-∠DAC=60°
(2)由(1)知,∠EDF=∠EDC+∠CDF=75°
∴∠ADF=∠EDF
在△ADF与△EDF中
∴△ADF≌△EDF(SAS)
∴AF=EF
18
①证明:∵正方形中,
∴AD=CD,∠ADC=90°,
∵,
∴∠EDF=90°,
∴∠ADE=∠CDF,
又∵∠A=∠DCF,
∴,
∴;
②连接EF,
∵,,
∴是等腰直角三角形,
∴EF=DF,
∵,,
∴PQ∥DF,
又∵PD∥QF,
∴四边形PDFQ是平行四边形,
∴PQ=DF,PD=QF,
∴EF=PQ,
∵QE+QF= QE+PD≥EF,即:.
19.
(1) ,
,
,
,
,
,即 ,
四边形 是平行四边形,
.
(2) 四边形 是菱形,
理由是: 点 为 中点,
,
,
,
,
四边形 是平行四边形,
,点 为 中点,
,
四边形 是菱形.
(3) 当 时,
,
,
由()可知,四边形 是菱形,
,
,
四边形 是正方形.
20.
(1)证明:∵四边形ABCD是矩形,
∴OB=OD,
∵AECF,
∴∠E=∠F,∠OBE=∠ODF,
在△BOE与△DOF中,
,
∴△BOE≌△DOF(AAS);
(2)当EF⊥AC时,四边形AECF是菱形.
证明:∵△BOE≌△DOF,
∴OE=OF,
∵四边形ABCD是矩形,
∴OA=OC,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
21.
(1)∵四边形ABCD是菱形,
∴OC=AC,AC⊥BD,
∵DE=AC,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)∵在菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,
∵OA=AC=1,AC⊥BD,AD=2,
∴OD=,
∴在矩形OCED中,CE=OD=,
∴在Rt△ACE中,AE=.
22.
(1)证明:在△ABC和△ADC中,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
∴△ABF≌△ADF(SAS),
∴∠AFB=∠AFD,
∵∠CFE=∠AFB,
∴∠AFD=∠CFE,
∴∠BAC=∠DAC,∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
∵∠BAC=∠DAC,
∴∠BAC=∠ACD,
∴∠DAC=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)BE⊥CD时,∠BCD=∠EFD;理由如下:
∵四边形ABCD是菱形,
∴BC=CD,∠BCF=∠DCF,
∵CF=CF,
∴△BCF≌△DCF,
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠BCD=∠EFD.
23.
(1)四边形ADEF是平行四边形.
理由:∵△ABD,△EBC都是等边三角形,
∴AD=BD=AB,BC=BE=EC
∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.
∴∠DBE=∠ABC.
在△DBE和△ABC中
∵BD=BA
∠DBE=∠ABC
BE=BC,
∴△DBE≌△ABC.
∴DE=AC.
又∵△ACF是等边三角形,
∴AC=AF.
∴DE=AF.
同理可证:AD=EF,
∴四边形ADEF平行四边形;
(2)∵四边形ADEF是矩形,
∴∠DAF=90°.
∴∠BAC=360° ∠DAF ∠DAB ∠FAC=360° 90° 60° 60°=150°.
∴∠BAC=150°时,四边形ADEF是矩形.
(3)当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在,
理由如下:
若∠BAC=60°,则∠DAF=360° ∠BAC ∠DAB ∠FAC=360° 60° 60° 60°=180°
此时,点A. D. F共线,
∴以A. D. E. F为顶点的四边形不存在.
答案第1页,共2页
答案第1页,共2页
第18章《平行四边形》综合练习
一、单选题
1.在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(7,3) B.(8,2) C.(3,7) D.(5,3)
2.如图,四边形中,R、P分别是上的点,E、F分别是的中点,当点P在上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段的长逐渐增大 B.线段的长逐渐减小
C.线段的长不变 D.线段的长与点P的位置有关
3.点A、B、C、D在同一平面内,从(1),(2),(3),(4)这四个条件中任选两个,能使四边形是平行四边形的选法有( )种.
A.3 B.4 C.5 D.6
4.如图,长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使点D与点B重合,点C落在点H的位置,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
5.如图,矩形的对角线,相交于点O,.若,则四边形的周长为( ).
A.4 B.6 C.8 D.10
6.下列命题中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线相等,且有一个角是直角的平行四边形是正方形
C.四个角都相等的菱形是正方形
D.对角线互相垂直平分且有一组邻边相等的四边形是正方形
7.若菱形的周长为8,高为1,则菱形两邻角的度数比为( )
A.3∶1 B.4∶1 C.5∶1 D.6∶1
8.如图,正方形的边长为8,点M在上,且,N是上一动点,则的最小值为( ).
A.8 B. C. D.10
9.某街区街道如图所示,其中垂直平分.从B站到E站有两条公交线路;线路1是,线路2是,则两条线路的长度关系为( )
A.路线1较短 B.路线2较短
C.两条路线长度相等 D.两条线路长度不确定
10.在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为( )
A. B. C.或 D.或
二、填空题
11.如图,中,,则的长为_________.
12.在中,已知对角线交于点O,的周长为17,,那么对角线_________.
13.如图,在中,,于E,则_______.
14.过对角线交点O作直线m,分别交直线于点E,交直线于点F,若,则的长是_________.
15.如图,在四边形中,,且,点P,Q分别从A,C两点同时出发,点P以的速度由A向D运动,点Q以的速度由向C运动B,则_____秒后四边形成为一个平行四边形.
三、解答题
16.如图,,,,分别是正方形各边的中点.四边形是什么四边形?为什么?
17.如图,以正方形的边长作等边和交于点F,连接.
(1)求的度数;
(2)求证:.
18.正方形中,E为边上的任意一点,交边的延长线于点F,
①如图1,求证:;
②若直线分别交边于P、Q,如图2,求证:.
19.如图,在 中,,过点 的直线MN//AB,为 边上一点,过点 作 ,垂足为点 ,交直线 于点 ,连接 ,.
(1)求证:;
(2)当 为 中点时,四边形 是什么特殊四边形 说明你的理由;
(3)在()的条件下,当 的大小满足什么条件时,四边形 是正方形 请说明你的理由.
20.已知:如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别相交于点E、F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?并给出证明.
21.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
22.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
23.如图,已知以△ABC的三边为边在BC的同侧作等边△ABD,△BCE,△ACF,请回答下列问题:
(1)四边形ADEF是什么四边形?请说明理由.
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.C
3.B
4.A
5.C
6.C
7.C
8.D
9.C
10.C
11.
12.22
13.
14.10或2
15.2
16.
解:四边形是正方形,理由如下:
连接AC、BD.
∵E、F、G、H分别是正方形ABCD各边的中点,
∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=BD,EF=HG=AC,
∴四边形EFGH为平行四边形,
∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,
∴EF=FG,EF⊥FG,
∴ EFGH是正方形.
17.
(1)∵四边形ABCD是正方形
∴AD=CD=BC,∠ADC=∠BCD=90°,∠DAC=∠BCF=∠DCF=45°
∵△DCE是等边三角形
∴CD=CE=DE,∠EDC=∠ECD=60°
∴BC=CE=AD=DE,∠BCE=∠BCD+∠ECD=150°
∴△BCE是等腰三角形
∴∠CBF=∠CEB=
在△CDF与△CBF中
∴△CBF≌△CDF(SAS)
∴∠CDF=∠CBF=15°
∴∠ADF=90°-∠CDF=75°
在△ADF中,∠AFD=180°-∠ADF-∠DAC=60°
(2)由(1)知,∠EDF=∠EDC+∠CDF=75°
∴∠ADF=∠EDF
在△ADF与△EDF中
∴△ADF≌△EDF(SAS)
∴AF=EF
18
①证明:∵正方形中,
∴AD=CD,∠ADC=90°,
∵,
∴∠EDF=90°,
∴∠ADE=∠CDF,
又∵∠A=∠DCF,
∴,
∴;
②连接EF,
∵,,
∴是等腰直角三角形,
∴EF=DF,
∵,,
∴PQ∥DF,
又∵PD∥QF,
∴四边形PDFQ是平行四边形,
∴PQ=DF,PD=QF,
∴EF=PQ,
∵QE+QF= QE+PD≥EF,即:.
19.
(1) ,
,
,
,
,
,即 ,
四边形 是平行四边形,
.
(2) 四边形 是菱形,
理由是: 点 为 中点,
,
,
,
,
四边形 是平行四边形,
,点 为 中点,
,
四边形 是菱形.
(3) 当 时,
,
,
由()可知,四边形 是菱形,
,
,
四边形 是正方形.
20.
(1)证明:∵四边形ABCD是矩形,
∴OB=OD,
∵AECF,
∴∠E=∠F,∠OBE=∠ODF,
在△BOE与△DOF中,
,
∴△BOE≌△DOF(AAS);
(2)当EF⊥AC时,四边形AECF是菱形.
证明:∵△BOE≌△DOF,
∴OE=OF,
∵四边形ABCD是矩形,
∴OA=OC,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
21.
(1)∵四边形ABCD是菱形,
∴OC=AC,AC⊥BD,
∵DE=AC,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)∵在菱形ABCD中,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2,
∵OA=AC=1,AC⊥BD,AD=2,
∴OD=,
∴在矩形OCED中,CE=OD=,
∴在Rt△ACE中,AE=.
22.
(1)证明:在△ABC和△ADC中,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
在△ABF和△ADF中,
∴△ABF≌△ADF(SAS),
∴∠AFB=∠AFD,
∵∠CFE=∠AFB,
∴∠AFD=∠CFE,
∴∠BAC=∠DAC,∠AFD=∠CFE;
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
∵∠BAC=∠DAC,
∴∠BAC=∠ACD,
∴∠DAC=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)BE⊥CD时,∠BCD=∠EFD;理由如下:
∵四边形ABCD是菱形,
∴BC=CD,∠BCF=∠DCF,
∵CF=CF,
∴△BCF≌△DCF,
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠BCD=∠EFD.
23.
(1)四边形ADEF是平行四边形.
理由:∵△ABD,△EBC都是等边三角形,
∴AD=BD=AB,BC=BE=EC
∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.
∴∠DBE=∠ABC.
在△DBE和△ABC中
∵BD=BA
∠DBE=∠ABC
BE=BC,
∴△DBE≌△ABC.
∴DE=AC.
又∵△ACF是等边三角形,
∴AC=AF.
∴DE=AF.
同理可证:AD=EF,
∴四边形ADEF平行四边形;
(2)∵四边形ADEF是矩形,
∴∠DAF=90°.
∴∠BAC=360° ∠DAF ∠DAB ∠FAC=360° 90° 60° 60°=150°.
∴∠BAC=150°时,四边形ADEF是矩形.
(3)当∠BAC=60°时,以A,D,E,F为顶点的四边形不存在,
理由如下:
若∠BAC=60°,则∠DAF=360° ∠BAC ∠DAB ∠FAC=360° 60° 60° 60°=180°
此时,点A. D. F共线,
∴以A. D. E. F为顶点的四边形不存在.
答案第1页,共2页
答案第1页,共2页
