北师大版七年级数学下册课件 第一章《整式的乘除》复习课(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册课件 第一章《整式的乘除》复习课(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 387.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 09:26:51 | ||
图片预览






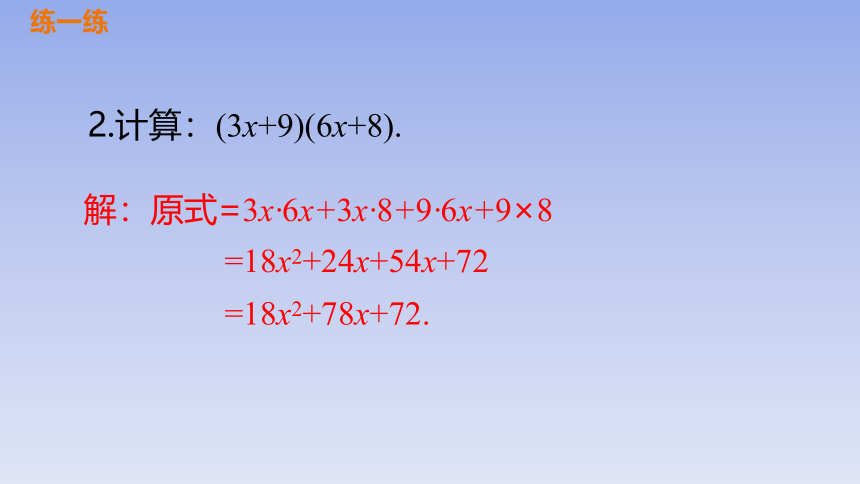

文档简介
(共23张PPT)
第一章 整式的乘除——复习题
版 本:北京师范大学出版社
章 节:七年级下册 第一章 整式的乘除
1. 梳理本章知识结构,能够灵活运用幂的运算法则、整式乘法法则、除法法则等工具进行计算;
2. 通过具体问题的解决,能体会数学中的转化思想、整体思想、分类讨论思想、数形结合思想.
学习目标
整
式
的
乘
除
幂的运算
单项式÷单项式
多项式÷单项式
同底数幂的乘法
幂的乘方
积的乘方
单项式×单项式
单项式×多项式
多项式×多项式
平方差公式
完全平方公式
同底数幂的除法
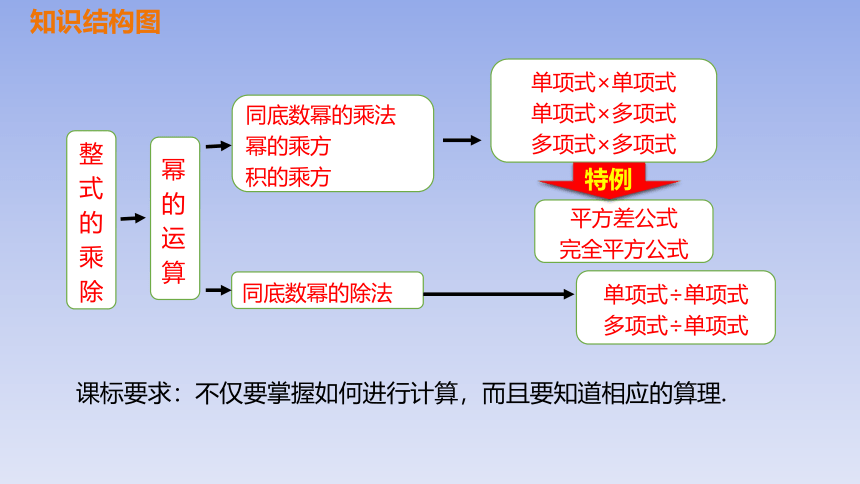
课标要求:不仅要掌握如何进行计算,而且要知道相应的算理.
特例
知识结构图
1.同底数幂的乘法
2.幂的乘方
3.积的乘方
4.同底数幂的除法
am÷an=am - n
am·an=am+n
幂的运算
5.零指数幂、负指数幂
6.科学记数法
(1)任何不等于零的数的零次幂都等于1.
(2)负整数指数幂:
幂的运算
1.下列计算不正确的是( )
A.2a3·a=2a4 B. (-a3)2=a6
C. a4 ·a3=a7 D. a6÷a2=a3
D
练一练
1.单项式与单项式相乘,把它们的 分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个 .
系数、相同字母的幂
因式
2.单项式与多项式相乘,就是根据 用 去乘 的每一项再把所得的积 .
单项式
多项式
相加
乘法分配律
3.多项式与多项式相乘,先用一个多项式的 乘另一个多项式的 ,再把所得的积 .
每一项
每一项
相加
整式的乘法
2.计算:(3x+9)(6x+8).
解:原式=3x·6x+3x·8+9·6x+9×8
=18x2+24x+54x+72
=18x2+78x+72.
练一练
将要解决的问题转化为另一个较易解决的问题,这是初中数学中常用的思想方法.
如本章中,多项式×多项式 单项式×多项式 单项式×单项式 有理数的乘法和同底数幂的乘法.
转化思想
名称 单项式除以单项式 多项式除以单项式
方法
项数 1 多项式的项数
逆运算 单项式乘以单项式 单项式乘以多项式
(1)系数除以系数
(2)同底数的幂相除
(3)只在被除式中出现的字母,照写
多项式的每一项分别除以单项式,再把所得的商相加
整式的除法
公式名称 平方差公式 完全平方公式
文字表示 两数和与这两数的差的积,等于这两数的平方的差 两数和(差)的平方,等于
这两数的_________加上(减去)___________的2倍
式子表示 (a+b)(a-b)= (a±b)2=
平方和
这两数积
a2-b2
a2±2ab+b2
[点拨]
(1)乘法公式实际上是一种特殊形式的多项式的乘法,公式的主要作用是简化运算;
(2)公式中的字母可以表示数,也可以表示其他单项式或多项式.
乘法公式
针对训练3:(课本34页第7题)
先化简,再求值:[(xy+2)(xy-2)-2x2y2+4]÷xy ,其中x=10,y= .
解:原式= [x2y2-4-2x2y2+4]÷xy
=-x2y2÷xy
=-xy
当x=10 ,y= 时,原式=
乘法公式应用——化简求值
学以致用
针对训练4:(课本34页第9题) 计算899×901+1.
解:899×901+1
=(900-1)×(900+1)+1
=9002-12+1
=810000
乘法公式应用——简化运算
学以致用
针对训练5:(课本34页第6题(2))计算(x+y+z)(x+y-z).
解:原式=[(x+y)+z][(x+y)-z]
=(x+y)2-z2
=x2+2xy+y2-z2.
乘法公式应用——简化运算
学以致用
针对训练6:若 4x2-axy+9y2是完全平方式,则a=________.
变式:多项式16x2+1加上一个单项式后,能使它成为一个整式的完全平方式,则可以加上的单项式共有___个,分别是_____________________________.
±12
5
-1、-16x2、±8x、64x4
分类讨论思想
乘法公式变形——知二求二
变式:若 ,则 __ , __.
针对训练7:已知a+b=5,ab=8,则a2+b2的值为____.
3
9
7
乘法公式变形——知二求二
乘法公式应用——几何意义
针对训练8:(课本35页第14题)请在图中指出面积为(a+3b)2的图形,并指出图中有多少个边长为a的正方形,有多少个边长为b的正方形,有多少个两边分别为a和b的长方形,然后用相应的公式进行验证.
数形结合思想
变式:(课本35页第13题)请分别准备几张如图所示的三种卡片A、B、C,用它们拼一些新的长方形,并计算它的面积.
a
b
a
b
a
b
通过本节课的学习,你有哪些收获?
运算算理
思想方法
转化思想
整体思想
分类讨论思想
数形结合思想
幂的运算
整式的乘除
课堂小结
课堂评价
课后复习题:
P34 7、10、
P35 12、13、
P36 17、18(选做)
课后作业
第一章 整式的乘除——复习题
版 本:北京师范大学出版社
章 节:七年级下册 第一章 整式的乘除
1. 梳理本章知识结构,能够灵活运用幂的运算法则、整式乘法法则、除法法则等工具进行计算;
2. 通过具体问题的解决,能体会数学中的转化思想、整体思想、分类讨论思想、数形结合思想.
学习目标
整
式
的
乘
除
幂的运算
单项式÷单项式
多项式÷单项式
同底数幂的乘法
幂的乘方
积的乘方
单项式×单项式
单项式×多项式
多项式×多项式
平方差公式
完全平方公式
同底数幂的除法
课标要求:不仅要掌握如何进行计算,而且要知道相应的算理.
特例
知识结构图
1.同底数幂的乘法
2.幂的乘方
3.积的乘方
4.同底数幂的除法
am÷an=am - n
am·an=am+n
幂的运算
5.零指数幂、负指数幂
6.科学记数法
(1)任何不等于零的数的零次幂都等于1.
(2)负整数指数幂:
幂的运算
1.下列计算不正确的是( )
A.2a3·a=2a4 B. (-a3)2=a6
C. a4 ·a3=a7 D. a6÷a2=a3
D
练一练
1.单项式与单项式相乘,把它们的 分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个 .
系数、相同字母的幂
因式
2.单项式与多项式相乘,就是根据 用 去乘 的每一项再把所得的积 .
单项式
多项式
相加
乘法分配律
3.多项式与多项式相乘,先用一个多项式的 乘另一个多项式的 ,再把所得的积 .
每一项
每一项
相加
整式的乘法
2.计算:(3x+9)(6x+8).
解:原式=3x·6x+3x·8+9·6x+9×8
=18x2+24x+54x+72
=18x2+78x+72.
练一练
将要解决的问题转化为另一个较易解决的问题,这是初中数学中常用的思想方法.
如本章中,多项式×多项式 单项式×多项式 单项式×单项式 有理数的乘法和同底数幂的乘法.
转化思想
名称 单项式除以单项式 多项式除以单项式
方法
项数 1 多项式的项数
逆运算 单项式乘以单项式 单项式乘以多项式
(1)系数除以系数
(2)同底数的幂相除
(3)只在被除式中出现的字母,照写
多项式的每一项分别除以单项式,再把所得的商相加
整式的除法
公式名称 平方差公式 完全平方公式
文字表示 两数和与这两数的差的积,等于这两数的平方的差 两数和(差)的平方,等于
这两数的_________加上(减去)___________的2倍
式子表示 (a+b)(a-b)= (a±b)2=
平方和
这两数积
a2-b2
a2±2ab+b2
[点拨]
(1)乘法公式实际上是一种特殊形式的多项式的乘法,公式的主要作用是简化运算;
(2)公式中的字母可以表示数,也可以表示其他单项式或多项式.
乘法公式
针对训练3:(课本34页第7题)
先化简,再求值:[(xy+2)(xy-2)-2x2y2+4]÷xy ,其中x=10,y= .
解:原式= [x2y2-4-2x2y2+4]÷xy
=-x2y2÷xy
=-xy
当x=10 ,y= 时,原式=
乘法公式应用——化简求值
学以致用
针对训练4:(课本34页第9题) 计算899×901+1.
解:899×901+1
=(900-1)×(900+1)+1
=9002-12+1
=810000
乘法公式应用——简化运算
学以致用
针对训练5:(课本34页第6题(2))计算(x+y+z)(x+y-z).
解:原式=[(x+y)+z][(x+y)-z]
=(x+y)2-z2
=x2+2xy+y2-z2.
乘法公式应用——简化运算
学以致用
针对训练6:若 4x2-axy+9y2是完全平方式,则a=________.
变式:多项式16x2+1加上一个单项式后,能使它成为一个整式的完全平方式,则可以加上的单项式共有___个,分别是_____________________________.
±12
5
-1、-16x2、±8x、64x4
分类讨论思想
乘法公式变形——知二求二
变式:若 ,则 __ , __.
针对训练7:已知a+b=5,ab=8,则a2+b2的值为____.
3
9
7
乘法公式变形——知二求二
乘法公式应用——几何意义
针对训练8:(课本35页第14题)请在图中指出面积为(a+3b)2的图形,并指出图中有多少个边长为a的正方形,有多少个边长为b的正方形,有多少个两边分别为a和b的长方形,然后用相应的公式进行验证.
数形结合思想
变式:(课本35页第13题)请分别准备几张如图所示的三种卡片A、B、C,用它们拼一些新的长方形,并计算它的面积.
a
b
a
b
a
b
通过本节课的学习,你有哪些收获?
运算算理
思想方法
转化思想
整体思想
分类讨论思想
数形结合思想
幂的运算
整式的乘除
课堂小结
课堂评价
课后复习题:
P34 7、10、
P35 12、13、
P36 17、18(选做)
课后作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
