2021-2022学年高一下学期数学人教A版(2019)必修第二册6.4.3.1余弦定理课件(16张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册6.4.3.1余弦定理课件(16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
6.4.3.1余弦定理
情景一
如图所示,这是学校后面的一个
池塘,甲同学想测量AB两,点之间
的距离,乙同学想了一个办法,他
在池塘外选定了,点C,测得AC之间
8m
的距离为6m,BC之间的距离为
8m,角C等于90°。他说这样就
可以测得AB两点之间的距离了
情景二
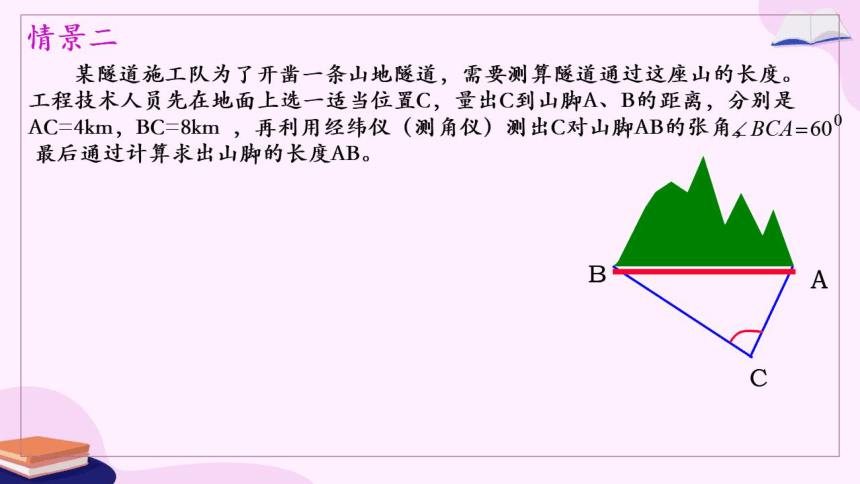
某隧道施工队为了开凿一条山地隧道,需要测算隧道通过这座山的长度。
工程技术人员先在地面上选一适当位置C,量出C到山脚A、B的距离,分别是
AC=4km,BC=8km,再利用经纬仪(测角仪)测出C对山脚AB的张角4BCA=609
最后通过计算求出山脚的长度AB。
B
A
C
情景三
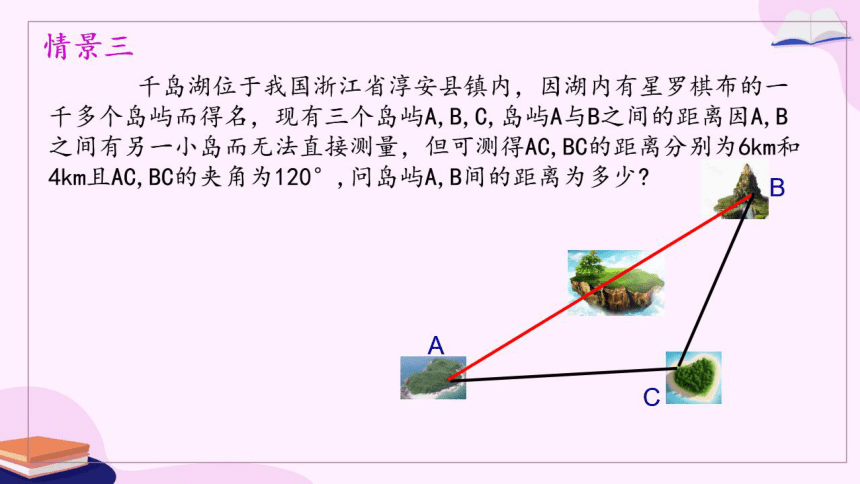
千岛湖位于我国浙江省淳安县镇内,因湖内有星罗棋布的一
千多个岛屿而得名,现有三个岛屿A,B,C,岛屿A与B之间的距离因A,B
之间有另一小岛而无法直接测量,但可测得AC,BC的距离分别为6k和
4km且AC,BC的夹角为120°,问岛屿A,B间的距离为多少?
B
问题探究
情景1:如图所示,在△ABC中,AC=6,BC=8,∠C=90°,求AB的长
情景2:如图所示,在△ABC中,AC=4,BC=8,∠C=60°,求AB的长
情景3:如图所示,在△ABC中,AC=6,BC=4,∠C=1200,求AB的长
[问题1]已知三角形的两边及其夹角,三角形能够确定吗?为什么
可以SAS
探索新知
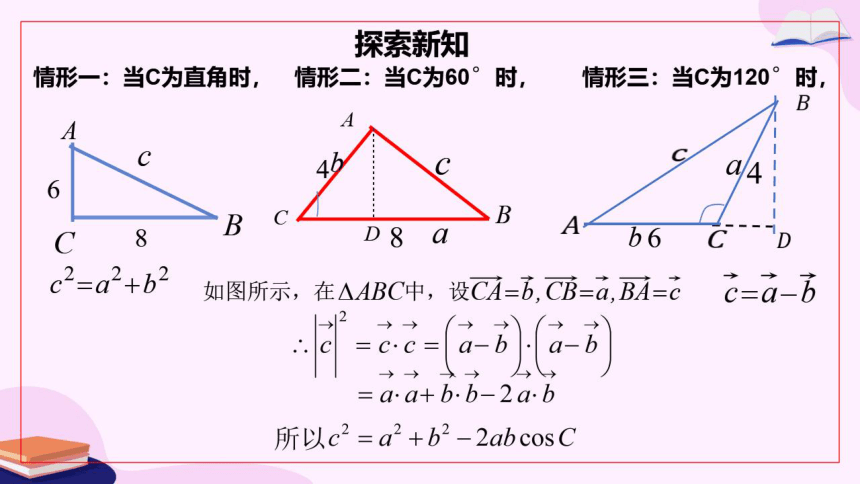
情形一:当C为直角时,
情形二:当C为60°时,
情形三:当C为120°时,
B
C
B
8
a
A
b6
c2=a2+b2
如图所示,在△ABC中,设CA=b,CB=a,BA=c
i c=a-b
剑
/2
a.a+b.
b-
-2ab
所以c2=a2+b2-2 ab cos C
结论:综上,我们得到:在△ABC中,有
c2=a2+b2-2abcosC
b2 a2+c2-2accos B
a2 b2 +c2-2bccos A
「问题3]你能用文字语句来描述余弦定理吗?
三角形任一边的平方等于其他两边平方的和减去这两边与它们
夹角的余弦的积的两倍.
一般地,三角形的三个角A,B,C和它们的对边4,b,c
叫做三角形的元素,已知三角形的几个元素求其它元素的过
程叫做解三角形。
[问题4]余弦定理中涉及了三角形中的那些量?
三角形中的三个边,和一个角共四个量
[问题51那么在求解三角形中是不是必须是已知两边和夹角才能
求解第四量?知三求一
[问题6]那么你能对有可能出现的其他情况进行分类吗?
1:已知三角形的两边及夹角求边
确定
2:已知三角形的两边及一边的对角求边
3:已知三角形的三边求角
确定
6.4.3.1余弦定理
情景一
如图所示,这是学校后面的一个
池塘,甲同学想测量AB两,点之间
的距离,乙同学想了一个办法,他
在池塘外选定了,点C,测得AC之间
8m
的距离为6m,BC之间的距离为
8m,角C等于90°。他说这样就
可以测得AB两点之间的距离了
情景二
某隧道施工队为了开凿一条山地隧道,需要测算隧道通过这座山的长度。
工程技术人员先在地面上选一适当位置C,量出C到山脚A、B的距离,分别是
AC=4km,BC=8km,再利用经纬仪(测角仪)测出C对山脚AB的张角4BCA=609
最后通过计算求出山脚的长度AB。
B
A
C
情景三
千岛湖位于我国浙江省淳安县镇内,因湖内有星罗棋布的一
千多个岛屿而得名,现有三个岛屿A,B,C,岛屿A与B之间的距离因A,B
之间有另一小岛而无法直接测量,但可测得AC,BC的距离分别为6k和
4km且AC,BC的夹角为120°,问岛屿A,B间的距离为多少?
B
问题探究
情景1:如图所示,在△ABC中,AC=6,BC=8,∠C=90°,求AB的长
情景2:如图所示,在△ABC中,AC=4,BC=8,∠C=60°,求AB的长
情景3:如图所示,在△ABC中,AC=6,BC=4,∠C=1200,求AB的长
[问题1]已知三角形的两边及其夹角,三角形能够确定吗?为什么
可以SAS
探索新知
情形一:当C为直角时,
情形二:当C为60°时,
情形三:当C为120°时,
B
C
B
8
a
A
b6
c2=a2+b2
如图所示,在△ABC中,设CA=b,CB=a,BA=c
i c=a-b
剑
/2
a.a+b.
b-
-2ab
所以c2=a2+b2-2 ab cos C
结论:综上,我们得到:在△ABC中,有
c2=a2+b2-2abcosC
b2 a2+c2-2accos B
a2 b2 +c2-2bccos A
「问题3]你能用文字语句来描述余弦定理吗?
三角形任一边的平方等于其他两边平方的和减去这两边与它们
夹角的余弦的积的两倍.
一般地,三角形的三个角A,B,C和它们的对边4,b,c
叫做三角形的元素,已知三角形的几个元素求其它元素的过
程叫做解三角形。
[问题4]余弦定理中涉及了三角形中的那些量?
三角形中的三个边,和一个角共四个量
[问题51那么在求解三角形中是不是必须是已知两边和夹角才能
求解第四量?知三求一
[问题6]那么你能对有可能出现的其他情况进行分类吗?
1:已知三角形的两边及夹角求边
确定
2:已知三角形的两边及一边的对角求边
3:已知三角形的三边求角
确定
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
