2021-2022学年苏科版七年级下册数学 第7章平面图形的认识(二) 练习(word版含简单答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级下册数学 第7章平面图形的认识(二) 练习(word版含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 275.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 10:48:45 | ||
图片预览



文档简介
平面图形的认识(二)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.(2021·重庆市第九十五初级中学校七年级阶段练习)下列每组数分别是三根小木棒的长度,不能用它们搭成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,4cm
C.3cm,4cm,5cm D.5cm,6cm,7cm
2.(2021·全国·八年级专题练习)如图,若,,则:①;②;③平分;④;⑤,其中正确的结论是
A.1个 B.2个 C.3个 D.4个
3.(2022·全国·七年级)如图,若,则下列结论正确的是( )
A. B. C. D.
4.(2021·全国·七年级专题练习)如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
5.(2021·全国·八年级专题练习)下列说法不正确的是( )
A.三角形的中线在三角形的内部
B.三角形的角平分线在三角形的内部
C.三角形的高在三角形的内部
D.三角形必有一高线在三角形的内部
6.(2021·全国·七年级课时练习)下列长度的三条线段能组成三角形的是( )
A.5,6,11 B.5,6,10 C.3,4,8 D.4a,4a,8a(a>0)
7.(2021·广东实验中学越秀学校八年级期中)赵师傅在做完门框后,为防止变形,按图中所示的方法在门上钉了两根斜拉的木条(图中的两根木条),其中运用的几何原理是( )
A.两点之间线段最短 B.三角形两边之和大于第三边
C.垂线段最短 D.三角形的稳定性
8.(2021·四川省德阳中学校八年级阶段练习)下列说法中,正确的个数有( )
①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°;
③三角形的外角大于与它不相邻的任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;
A.1个 B.2个 C.3个 D.4
9.(2021·四川绵阳·中考真题)如图,有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17°
10.(2021·甘肃甘肃·中考真题)如图,足球图片正中的黑色正五边形的内角和是( ).
A.180° B.360° C.540° D.720°
11.(2021·江苏·苏州新草桥中学一模)如图,直线EF直线GH,Rt△ABC中,∠C=90°,顶点A在GH上,顶点B在EF上,且BA平分∠DBE,若∠CAD=26°,则∠BAD的度数为( )
A.26° B.32° C.34° D.45°
12.(2022·江苏·七年级专题练习)在一次数学课上,老师让学生进行画图,你觉得学生可能会发现的结论是( )
A.三条线段首尾顺次相接能构成三角形
B.三角形的内角和是180°
C.三角形的任意一个外角大于和它不相邻的内角
D.三角形任意两边之和大于第三边
13.(2022·江苏·七年级专题练习)如图,中,,将沿DE折叠,点A落在F处,则的度数为( )
A. B. C. D.
14.(2021·全国·八年级专题练习)如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=( )
A.80° B.70° C.60° D.90°
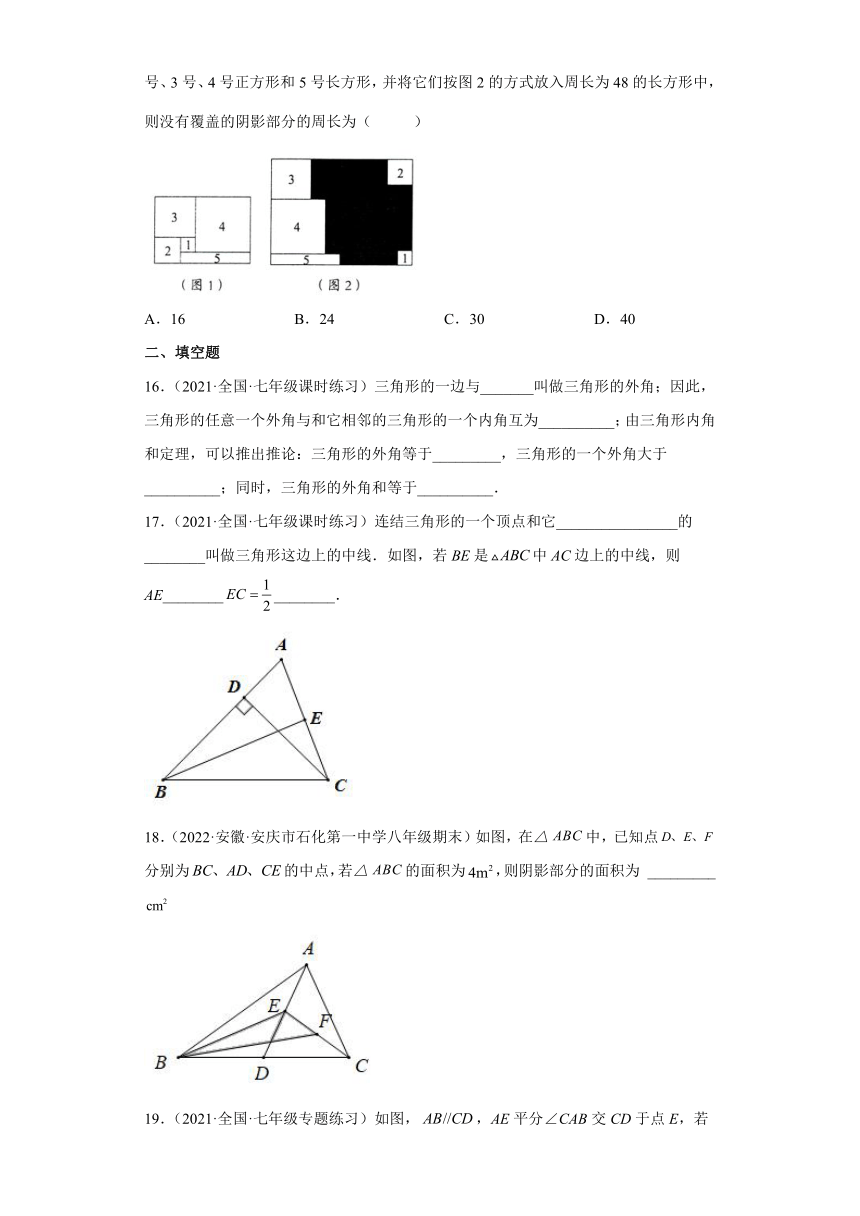
15.(2021·浙江湖州·七年级阶段练习)将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图2的方式放入周长为48的长方形中,则没有覆盖的阴影部分的周长为( )
A.16 B.24 C.30 D.40
二、填空题
16.(2021·全国·七年级课时练习)三角形的一边与_______叫做三角形的外角;因此,三角形的任意一个外角与和它相邻的三角形的一个内角互为__________;由三角形内角和定理,可以推出推论:三角形的外角等于_________,三角形的一个外角大于__________;同时,三角形的外角和等于__________.
17.(2021·全国·七年级课时练习)连结三角形的一个顶点和它________________的________叫做三角形这边上的中线.如图,若BE是中AC边上的中线,则AE________________.
18.(2022·安徽·安庆市石化第一中学八年级期末)如图,在△中,已知点分别为的中点,若△的面积为,则阴影部分的面积为 _________
19.(2021·全国·七年级专题练习)如图,,AE平分∠CAB交CD于点E,若,则___.
20.(2021·全国·八年级专题练习)如图,D,E,F分别是的边,,上的中点,连接,,交于点G,,的面积为6,设的面积为,的面积为,则=______.
21.(2022·江苏·七年级专题练习)如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
22.(2022·江苏·七年级专题练习)如图,在△ABC,AD 是角平分线,AE 是中线,AF 是高.如果BC=10cm,那么 BE=_____;∠ABC=40°,∠ACB=60°,那么∠DAF=_____°.
23.(2020·全国·八年级单元测试)如图中,是边上的中线,是中边上的中线,若的面积是24,,则点到的距离是___.
24.(2021·浙江衢州·中考真题)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.
25.(2013·浙江绍兴·中考真题)如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是__
三、解答题
26.(2020·云南玉溪·七年级期中)如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.
解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
27.(2021·全国·七年级课时练习)如图是一块电脑主板的示意图,每一个转角处都是直角,数据如图所示,则该主板的周长是多少?
28.(2021·江苏·七年级专题练习)如图,∠ABC与∠DEF的两边分别交于点M、N.若∠ABC=∠DEF,且AB∥EF.试说明BC∥DE.
29.(2021·全国·八年级专题练习)如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
30.(2021·全国·八年级专题练习)两条直线相交所形成的较小的角称为这两条直线的夹角.如:直线m、n相交,其夹角为60°,特别的,如果m⊥n,那么其夹角为90°.
(1)如图①,MN∥PQ,含45°的直角三角形ABC的三边和两条平行线有4个交点D、E、F、G,若AB和PQ的夹角为65°,求∠CFQ与∠CEN的度数.
(2)如图②,MN∥PQ,将一块含45°的直角三角板ABC任意摆放在两条平行线上(三角板足够大),使三角板的三边和两条平行线始终有4个交点.设斜边AB所在直线与MN(或PQ)的夹角为α(0°<α≤90°),直接写出4个交点处的夹角之和.(结果可以用含α的代数式表示)
试卷第1页,共3页
参考答案:
1.A
2.C
3.A
4.B
5.C
6.B
7.D
8.C
9.C
10.C
11.B
12.D
13.B
14.A
15.D
16. 另一边的延长线组成的角 邻补角 与它不相邻的两个内角的和 任何一个与它不相邻的内角
17. 所对边的中点 线段 = AC
18.1
19.125°
20.
21.13
22. 5 cm 10
23.2
24.72°
25.12°.
26.对顶角相等;∠2;AB;CD;同位角相等,两直线平行;EF.
27.该主板的周长是.
28.略29.略
30.(1)20°;70°;(2)90°+2α或4α-90°或270°或4α+90°或135°+2α或180°.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.(2021·重庆市第九十五初级中学校七年级阶段练习)下列每组数分别是三根小木棒的长度,不能用它们搭成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,4cm
C.3cm,4cm,5cm D.5cm,6cm,7cm
2.(2021·全国·八年级专题练习)如图,若,,则:①;②;③平分;④;⑤,其中正确的结论是
A.1个 B.2个 C.3个 D.4个
3.(2022·全国·七年级)如图,若,则下列结论正确的是( )
A. B. C. D.
4.(2021·全国·七年级专题练习)如图,已知在△ABC中,∠C=90°,BE平分∠ABC,且BE∥AD,∠BAD=20°,则∠AEB的度数为( )
A.100° B.110° C.120° D.130°
5.(2021·全国·八年级专题练习)下列说法不正确的是( )
A.三角形的中线在三角形的内部
B.三角形的角平分线在三角形的内部
C.三角形的高在三角形的内部
D.三角形必有一高线在三角形的内部
6.(2021·全国·七年级课时练习)下列长度的三条线段能组成三角形的是( )
A.5,6,11 B.5,6,10 C.3,4,8 D.4a,4a,8a(a>0)
7.(2021·广东实验中学越秀学校八年级期中)赵师傅在做完门框后,为防止变形,按图中所示的方法在门上钉了两根斜拉的木条(图中的两根木条),其中运用的几何原理是( )
A.两点之间线段最短 B.三角形两边之和大于第三边
C.垂线段最短 D.三角形的稳定性
8.(2021·四川省德阳中学校八年级阶段练习)下列说法中,正确的个数有( )
①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°;
③三角形的外角大于与它不相邻的任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;
A.1个 B.2个 C.3个 D.4
9.(2021·四川绵阳·中考真题)如图,有一块含有30°角的直角三角形板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17°
10.(2021·甘肃甘肃·中考真题)如图,足球图片正中的黑色正五边形的内角和是( ).
A.180° B.360° C.540° D.720°
11.(2021·江苏·苏州新草桥中学一模)如图,直线EF直线GH,Rt△ABC中,∠C=90°,顶点A在GH上,顶点B在EF上,且BA平分∠DBE,若∠CAD=26°,则∠BAD的度数为( )
A.26° B.32° C.34° D.45°
12.(2022·江苏·七年级专题练习)在一次数学课上,老师让学生进行画图,你觉得学生可能会发现的结论是( )
A.三条线段首尾顺次相接能构成三角形
B.三角形的内角和是180°
C.三角形的任意一个外角大于和它不相邻的内角
D.三角形任意两边之和大于第三边
13.(2022·江苏·七年级专题练习)如图,中,,将沿DE折叠,点A落在F处,则的度数为( )
A. B. C. D.
14.(2021·全国·八年级专题练习)如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=( )
A.80° B.70° C.60° D.90°
15.(2021·浙江湖州·七年级阶段练习)将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图2的方式放入周长为48的长方形中,则没有覆盖的阴影部分的周长为( )
A.16 B.24 C.30 D.40
二、填空题
16.(2021·全国·七年级课时练习)三角形的一边与_______叫做三角形的外角;因此,三角形的任意一个外角与和它相邻的三角形的一个内角互为__________;由三角形内角和定理,可以推出推论:三角形的外角等于_________,三角形的一个外角大于__________;同时,三角形的外角和等于__________.
17.(2021·全国·七年级课时练习)连结三角形的一个顶点和它________________的________叫做三角形这边上的中线.如图,若BE是中AC边上的中线,则AE________________.
18.(2022·安徽·安庆市石化第一中学八年级期末)如图,在△中,已知点分别为的中点,若△的面积为,则阴影部分的面积为 _________
19.(2021·全国·七年级专题练习)如图,,AE平分∠CAB交CD于点E,若,则___.
20.(2021·全国·八年级专题练习)如图,D,E,F分别是的边,,上的中点,连接,,交于点G,,的面积为6,设的面积为,的面积为,则=______.
21.(2022·江苏·七年级专题练习)如图,BE、CE分别为的内、外角平分线,BF、CF分别为的内、外角平分线,若,则_______度.
22.(2022·江苏·七年级专题练习)如图,在△ABC,AD 是角平分线,AE 是中线,AF 是高.如果BC=10cm,那么 BE=_____;∠ABC=40°,∠ACB=60°,那么∠DAF=_____°.
23.(2020·全国·八年级单元测试)如图中,是边上的中线,是中边上的中线,若的面积是24,,则点到的距离是___.
24.(2021·浙江衢州·中考真题)如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.
25.(2013·浙江绍兴·中考真题)如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是__
三、解答题
26.(2020·云南玉溪·七年级期中)如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.
解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
27.(2021·全国·七年级课时练习)如图是一块电脑主板的示意图,每一个转角处都是直角,数据如图所示,则该主板的周长是多少?
28.(2021·江苏·七年级专题练习)如图,∠ABC与∠DEF的两边分别交于点M、N.若∠ABC=∠DEF,且AB∥EF.试说明BC∥DE.
29.(2021·全国·八年级专题练习)如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
30.(2021·全国·八年级专题练习)两条直线相交所形成的较小的角称为这两条直线的夹角.如:直线m、n相交,其夹角为60°,特别的,如果m⊥n,那么其夹角为90°.
(1)如图①,MN∥PQ,含45°的直角三角形ABC的三边和两条平行线有4个交点D、E、F、G,若AB和PQ的夹角为65°,求∠CFQ与∠CEN的度数.
(2)如图②,MN∥PQ,将一块含45°的直角三角板ABC任意摆放在两条平行线上(三角板足够大),使三角板的三边和两条平行线始终有4个交点.设斜边AB所在直线与MN(或PQ)的夹角为α(0°<α≤90°),直接写出4个交点处的夹角之和.(结果可以用含α的代数式表示)
试卷第1页,共3页
参考答案:
1.A
2.C
3.A
4.B
5.C
6.B
7.D
8.C
9.C
10.C
11.B
12.D
13.B
14.A
15.D
16. 另一边的延长线组成的角 邻补角 与它不相邻的两个内角的和 任何一个与它不相邻的内角
17. 所对边的中点 线段 = AC
18.1
19.125°
20.
21.13
22. 5 cm 10
23.2
24.72°
25.12°.
26.对顶角相等;∠2;AB;CD;同位角相等,两直线平行;EF.
27.该主板的周长是.
28.略29.略
30.(1)20°;70°;(2)90°+2α或4α-90°或270°或4α+90°或135°+2α或180°.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
