2021-2022学年湘教版八年级数学下册2.7正方形 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册2.7正方形 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 241.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 10:40:07 | ||
图片预览



文档简介
2021-2022学年湘教版八年级数学下册《2-7正方形》同步练习题(附答案)
一.选择题
1.正方形具有而菱形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对边相等 D.邻边相等
2.已知四边形ABCD是平行四边形,下列结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;
③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形,其中错误的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
4.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
5.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的面积为( )
A.8 B.12 C.16 D.20
6.正方形ABCD的一条对角线长为6,则这个正方形的面积是( )
A.9 B.18 C.24 D.36
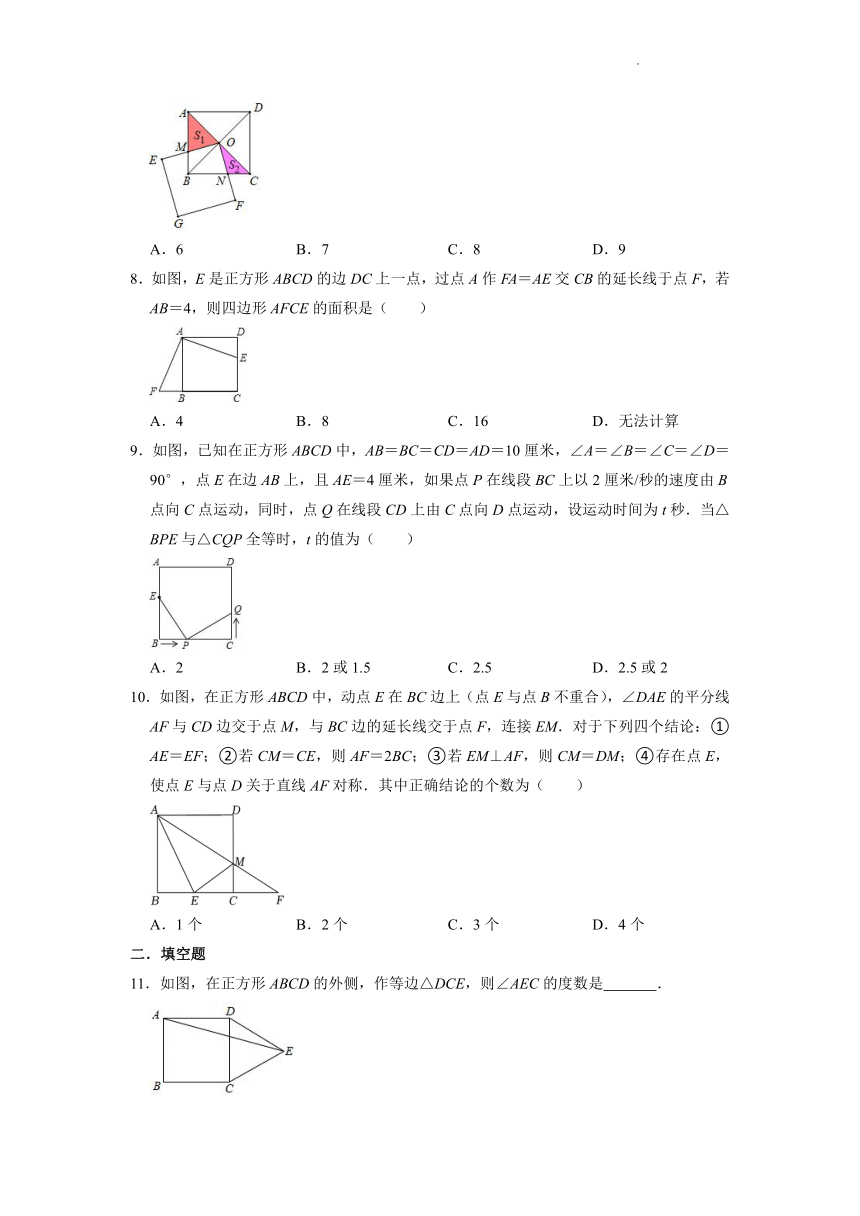
7.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记△AOM的面积为S1,△CON的面积为S2,若正方形的边长AB=10,S1=16,则S2的大小为( )
A.6 B.7 C.8 D.9
8.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
9.如图,已知在正方形ABCD中,AB=BC=CD=AD=10厘米,∠A=∠B=∠C=∠D=90°,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动时间为t秒.当△BPE与△CQP全等时,t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
10.如图,在正方形ABCD中,动点E在BC边上(点E与点B不重合),∠DAE的平分线AF与CD边交于点M,与BC边的延长线交于点F,连接EM.对于下列四个结论:①AE=EF;②若CM=CE,则AF=2BC;③若EM⊥AF,则CM=DM;④存在点E,使点E与点D关于直线AF对称.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,在正方形ABCD的外侧,作等边△DCE,则∠AEC的度数是 .
12.如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,AB=10,则EF的长为 .
13.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
14.如图,正方形ABCD的对角线相交于点O,正方形A'B'C'O与正方形ABCD的边长相等,若两个正方形的重叠部分(阴影部分)的面积为,则正方形A'B'C'O的面积为 .
15.如图,在正方形ABCD中,点E、F分别在对角线BD上,请你添加一个条件 ,使四边形AECF是菱形.
16.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4= .
三.解答题
17.如图,四边形ACMF、BCNE是两个正方形.求证:AN=BM.
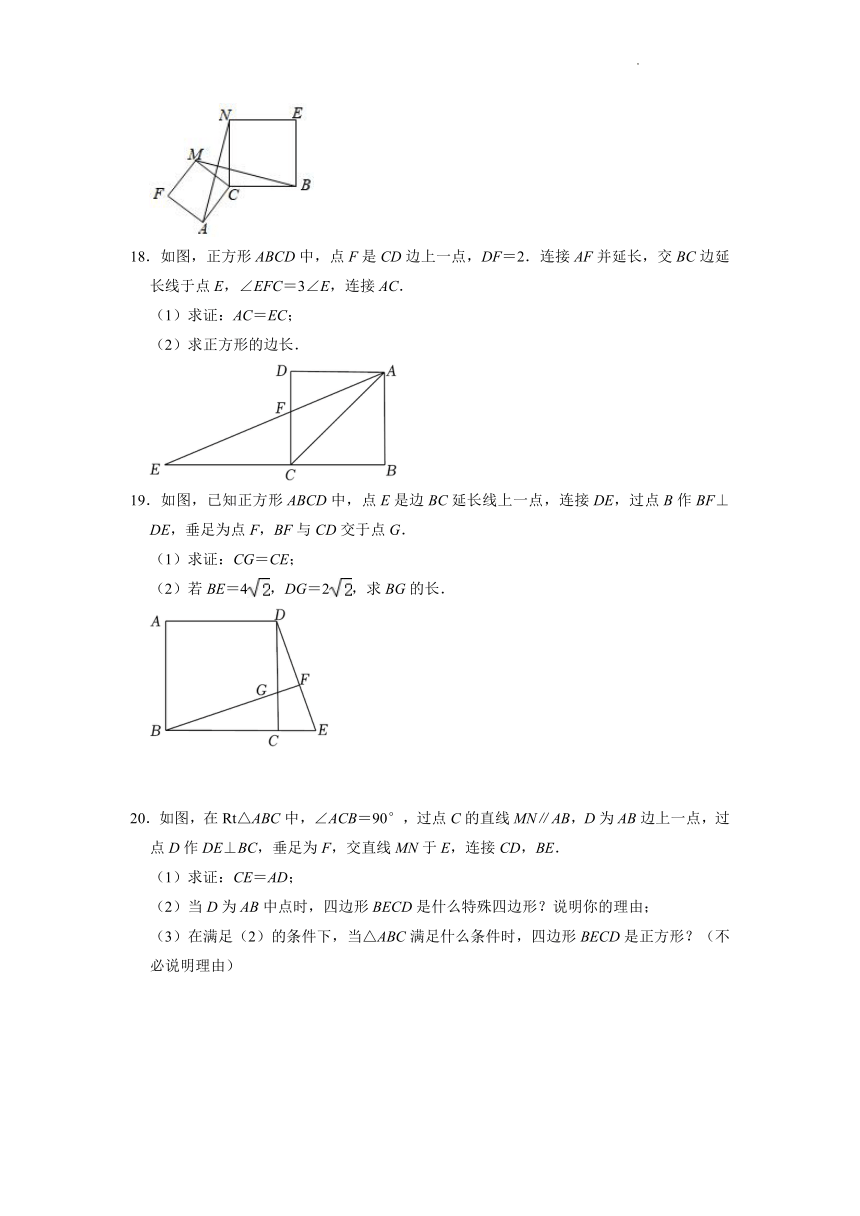
18.如图,正方形ABCD中,点F是CD边上一点,DF=2.连接AF并延长,交BC边延长线于点E,∠EFC=3∠E,连接AC.
(1)求证:AC=EC;
(2)求正方形的边长.
19.如图,已知正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD交于点G.
(1)求证:CG=CE;
(2)若BE=4,DG=2,求BG的长.
20.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
21.(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF=∠BAD,此时(1)中的结论是否仍然成立?请说明理由.
22.如图,点E,F分别是正方形ABCD的对角线AC上的两个动点,∠EBF=45°.求证:EF2=AE2+CF2.
参考答案
一.选择题
1.解:正方形具有而菱形不一定有的性质是:对角线相等.
故选:B.
2.解:∵四边形ABCD是平行四边形,
∴当AB=BC时,它是菱形,故①正确,
当AC⊥BD时,它是菱形,故②正确,
当∠ABC=90°时,它是矩形,故③正确,
当AC=BD时,它是矩形,不是正方形,故④错误,
故选:A.
3.解:因为矩形的四个角是直角,
故A正确,
因为菱形的对角线互相垂直,
故B正确,
因为正方形的对角线相等,
故C正确,
菱形的对角线和边长不一定相等,
例如:∠ABC=80°,因为AB=BC,所以∠BAC=∠ACB=50°,此时AC>AB,
故选:D.
4.解:在正方形ABCD中,AB=AD,∠BAD=90°,∠ABD=∠ADB=45°,
∵AB=BF=DE,
∴∠BAF=∠BFA=∠DAE=∠DEA=(180°﹣45°)÷2=67.5°,
∴AE=AF,
∴∠EAF=180°﹣2×67.5°=45°.
故选:C.
5.解:在菱形ABCD中,AB=BC=4,∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴正方形ACEF的边长为4,
∴正方形ACEF的面积为16,
故选:C.
6.解:在正方形中,对角线相等,所以正方形ABCD的对角线长均为6,
∵正方形又是菱形,
菱形的面积计算公式是S=ab(a、b是正方形对角线长度)
∴S=×6×6=18,
故选:B.
7.解:∵四边形ABCD和四边形OA'B'C'都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠A'OC'=90°,
∴∠A'OB=∠COC'.
在△OBM与△OCN中,
,
∴△OBM≌△OCN(ASA),
∴S1+S2=S△OAB=×10×10=25,
∴S2=25﹣16=9,
故选:D.
8.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
9.解:当点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∴BP=10﹣6=4厘米,
∴运动时间=4÷2=2(秒);
当点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t==(秒),
故选:D.
10.解:∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAF=∠EFA,
∴∠EFA=∠EAF,
∴AE=EF,故①正确;
若CM=CE,
则DM=BE,
∵∠B=∠D=90°,AB=AD,
在△ABE和△ADM中,
,
∴△ABE≌△ADM(SAS),
∴∠BAE=∠DAM=∠EAF=30°,
∴∠F=30°,
∴AF=2AB,
∴AF=2BC,故②正确;
若EM⊥AF,
∴M是AF的中点,
∴AM=FM,
在△ADM和△FMC中,
,
∴△ADM≌△FMC(AAS),
∴CM=DM,故③正确;
只有当点E和点D重合时,
才有点E与点D关于直线AF对称.
与题意不符,故④错误.
综上所述:其中正确结论有①②③,共3个,
故选:C.
二.填空题
11.解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°.
∵△CDE是等边三角形,
∴∠CDE=∠DEC=60°.
∴∠ADE=90°+60°=150°,
∵AD=DE,
∴∠DAE=∠DEA=(180°﹣∠ADE)÷2=15°,
∴∠AEC=∠DEC﹣∠AED=60°﹣15°=45°.
故答案为:45°.
12.解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAD+∠DAE=90°,
∵BF⊥a于点F,DE⊥a于点E,
∴∠AFB=∠AFD=90°,
∵∠BAF+∠ABF=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴AF=DE=8,BF=AE,
在Rt△ABF中,BF==6,
∴AE=6,
∴EF=AE+AF=6+8=14.
故答案为14.
13.解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA﹣AE=OC﹣CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF==2,
由勾股定理得:DE==2,
∴四边形BEDF的周长=4DE=4×2=8,
故答案为:8.
14.解:∵四边形ABCD和四边形OA'B'C'都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠A'OC'=90°,
∴∠A'OB=∠COC'.
在△OBM与△OCN中,
,
∴△OBM≌△OCN(ASA),
∴四边形OMBN的面积等于三角形BOC的面积,
即重叠阴影部分面积不变,总是等于正方形ABCD和正方形A'B'C'O面积的,
∴正方形A'B'C'O的面积为4.
故答案为:4.
.
15.解:添加的条件为:BE=DF,
理由:正方形ABCD中,对角线BD,
∴AB=BC=CD=DA,
∠ABE=∠CBE=∠CDF=∠ADF=45°.
∵BE=DF,
∴△ABE≌△CBE≌△DCF≌△DAF(SAS).
∴AE=CE=CF=AF,
∴四边形AECF是菱形;
故答案为:BE=DF.
16.解:如图,∵图中的四边形为正方形,
∴∠ABD=90°,AB=DB,
∴∠ABC+∠DBE=90°,
∵∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵DE2+BE2=BD2,
∴ED2+AC2=BD2,
∵S1=AC2,S2=DE2,BD2=1,
∴S1+S2=1,
同理可得S3+S4=3,
∴S1+S2+S3+S4=1+3=4.
故答案为4.
三.解答题
17.解:∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM,NC=BC,∠ACM=∠BCN=90°,
∵∠MCN=∠NCM,
∴∠ACN=∠BCM,
在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS),
∴AN=BM.
18.(1)证明:∵四边形ABCD是正方形,
∴∠DCE=90°,
∵∠EFC=3∠E,∠EFC+∠E=90°,
∴4∠E=90°,
∴∠E=22.5°,
又∵AC是正方形对角线,
∠ACB=45°,
∵∠ACB=∠E+∠EAC,
∴∠EAC=22.5°,
∴∠EAC=∠E,
∴AC=EC;
(2)解:设正方形的边长为x,则AC=EC=x,
∵AD∥BC,
∴∠DAF=∠E,
∵∠ADC=∠FDE=90°,
∴x=2+2,
∴正方形的边长为2+2.
19.(1)证明:∵四边形ABCD是正方形,
∴∠BCG=∠DCE=90°,BC=CD,
∵BF⊥DE,
∴∠DFG=∠BCG=90°,
∵∠BGC=∠DGF,
∴∠CBG=∠CDE.
在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS),
∴CG=CE;
(2)解:由(1)△BCG≌△DCE得CG=CE,
又∵BE=BC+CE=4,DG=CD﹣CG=2,
∴BC=3CG=,
在Rt△BCG中,BG===2.
20.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)解:当∠A=45°时,四边形BECD是正方形,
理由:∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
21.解:(1)如图1,
EF=BE+DF,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABM=90°,
又∵BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵∠EAF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=∠MAE=45°=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF,
(2)如图2,
EF=BE+DF,仍然成立,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠4=180°,
∴∠D=∠4,
又∵AB=AD,BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵,
∴∠1+∠3=∠EAF,
∴∠MAE=∠2+∠3=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF.
22.证明:如图,将△CBF绕点B逆时针旋转90°,可得△ABN,连接EN,
由旋转的性质可得BN=BF,AN=CF,∠BAN=∠BCF=45°,∠CBF=∠ABN,
∴∠CAN=∠CAB+∠BAN=90°,
∴EN2=AE2+AN2,
∵∠EBF=45°,
∴∠CBF+∠ABE=45°,
∴∠ABE+∠ABN=45°=∠NBE=∠EBF,
在△EBF和△EBN中,
,
∴△EBF≌△EBN(SAS),
∴EF=EN,
∴EF2=AE2+CF2.
一.选择题
1.正方形具有而菱形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对边相等 D.邻边相等
2.已知四边形ABCD是平行四边形,下列结论:①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;
③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形,其中错误的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
4.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
5.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的面积为( )
A.8 B.12 C.16 D.20
6.正方形ABCD的一条对角线长为6,则这个正方形的面积是( )
A.9 B.18 C.24 D.36
7.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记△AOM的面积为S1,△CON的面积为S2,若正方形的边长AB=10,S1=16,则S2的大小为( )
A.6 B.7 C.8 D.9
8.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
9.如图,已知在正方形ABCD中,AB=BC=CD=AD=10厘米,∠A=∠B=∠C=∠D=90°,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动时间为t秒.当△BPE与△CQP全等时,t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
10.如图,在正方形ABCD中,动点E在BC边上(点E与点B不重合),∠DAE的平分线AF与CD边交于点M,与BC边的延长线交于点F,连接EM.对于下列四个结论:①AE=EF;②若CM=CE,则AF=2BC;③若EM⊥AF,则CM=DM;④存在点E,使点E与点D关于直线AF对称.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.如图,在正方形ABCD的外侧,作等边△DCE,则∠AEC的度数是 .
12.如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,AB=10,则EF的长为 .
13.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
14.如图,正方形ABCD的对角线相交于点O,正方形A'B'C'O与正方形ABCD的边长相等,若两个正方形的重叠部分(阴影部分)的面积为,则正方形A'B'C'O的面积为 .
15.如图,在正方形ABCD中,点E、F分别在对角线BD上,请你添加一个条件 ,使四边形AECF是菱形.
16.在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1+S2+S3+S4= .
三.解答题
17.如图,四边形ACMF、BCNE是两个正方形.求证:AN=BM.
18.如图,正方形ABCD中,点F是CD边上一点,DF=2.连接AF并延长,交BC边延长线于点E,∠EFC=3∠E,连接AC.
(1)求证:AC=EC;
(2)求正方形的边长.
19.如图,已知正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD交于点G.
(1)求证:CG=CE;
(2)若BE=4,DG=2,求BG的长.
20.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
21.(1)如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系,并说明理由;
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF=∠BAD,此时(1)中的结论是否仍然成立?请说明理由.
22.如图,点E,F分别是正方形ABCD的对角线AC上的两个动点,∠EBF=45°.求证:EF2=AE2+CF2.
参考答案
一.选择题
1.解:正方形具有而菱形不一定有的性质是:对角线相等.
故选:B.
2.解:∵四边形ABCD是平行四边形,
∴当AB=BC时,它是菱形,故①正确,
当AC⊥BD时,它是菱形,故②正确,
当∠ABC=90°时,它是矩形,故③正确,
当AC=BD时,它是矩形,不是正方形,故④错误,
故选:A.
3.解:因为矩形的四个角是直角,
故A正确,
因为菱形的对角线互相垂直,
故B正确,
因为正方形的对角线相等,
故C正确,
菱形的对角线和边长不一定相等,
例如:∠ABC=80°,因为AB=BC,所以∠BAC=∠ACB=50°,此时AC>AB,
故选:D.
4.解:在正方形ABCD中,AB=AD,∠BAD=90°,∠ABD=∠ADB=45°,
∵AB=BF=DE,
∴∠BAF=∠BFA=∠DAE=∠DEA=(180°﹣45°)÷2=67.5°,
∴AE=AF,
∴∠EAF=180°﹣2×67.5°=45°.
故选:C.
5.解:在菱形ABCD中,AB=BC=4,∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴正方形ACEF的边长为4,
∴正方形ACEF的面积为16,
故选:C.
6.解:在正方形中,对角线相等,所以正方形ABCD的对角线长均为6,
∵正方形又是菱形,
菱形的面积计算公式是S=ab(a、b是正方形对角线长度)
∴S=×6×6=18,
故选:B.
7.解:∵四边形ABCD和四边形OA'B'C'都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠A'OC'=90°,
∴∠A'OB=∠COC'.
在△OBM与△OCN中,
,
∴△OBM≌△OCN(ASA),
∴S1+S2=S△OAB=×10×10=25,
∴S2=25﹣16=9,
故选:D.
8.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
9.解:当点Q的运动速度与点P的运动速度都是2厘米/秒,若△BPE≌△CQP,则BP=CQ,BE=CP,
∵AB=BC=10厘米,AE=4厘米,
∴BE=CP=6厘米,
∴BP=10﹣6=4厘米,
∴运动时间=4÷2=2(秒);
当点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△OQP全等,只要BP=PC=5厘米,CQ=BE=6厘米,即可.
∴点P,Q运动的时间t==(秒),
故选:D.
10.解:∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAF=∠EFA,
∴∠EFA=∠EAF,
∴AE=EF,故①正确;
若CM=CE,
则DM=BE,
∵∠B=∠D=90°,AB=AD,
在△ABE和△ADM中,
,
∴△ABE≌△ADM(SAS),
∴∠BAE=∠DAM=∠EAF=30°,
∴∠F=30°,
∴AF=2AB,
∴AF=2BC,故②正确;
若EM⊥AF,
∴M是AF的中点,
∴AM=FM,
在△ADM和△FMC中,
,
∴△ADM≌△FMC(AAS),
∴CM=DM,故③正确;
只有当点E和点D重合时,
才有点E与点D关于直线AF对称.
与题意不符,故④错误.
综上所述:其中正确结论有①②③,共3个,
故选:C.
二.填空题
11.解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°.
∵△CDE是等边三角形,
∴∠CDE=∠DEC=60°.
∴∠ADE=90°+60°=150°,
∵AD=DE,
∴∠DAE=∠DEA=(180°﹣∠ADE)÷2=15°,
∴∠AEC=∠DEC﹣∠AED=60°﹣15°=45°.
故答案为:45°.
12.解:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAD+∠DAE=90°,
∵BF⊥a于点F,DE⊥a于点E,
∴∠AFB=∠AFD=90°,
∵∠BAF+∠ABF=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴AF=DE=8,BF=AE,
在Rt△ABF中,BF==6,
∴AE=6,
∴EF=AE+AF=6+8=14.
故答案为14.
13.解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA﹣AE=OC﹣CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF==2,
由勾股定理得:DE==2,
∴四边形BEDF的周长=4DE=4×2=8,
故答案为:8.
14.解:∵四边形ABCD和四边形OA'B'C'都是正方形,
∴OB=OC,∠OBA=∠OCB=45°,∠BOC=∠A'OC'=90°,
∴∠A'OB=∠COC'.
在△OBM与△OCN中,
,
∴△OBM≌△OCN(ASA),
∴四边形OMBN的面积等于三角形BOC的面积,
即重叠阴影部分面积不变,总是等于正方形ABCD和正方形A'B'C'O面积的,
∴正方形A'B'C'O的面积为4.
故答案为:4.
.
15.解:添加的条件为:BE=DF,
理由:正方形ABCD中,对角线BD,
∴AB=BC=CD=DA,
∠ABE=∠CBE=∠CDF=∠ADF=45°.
∵BE=DF,
∴△ABE≌△CBE≌△DCF≌△DAF(SAS).
∴AE=CE=CF=AF,
∴四边形AECF是菱形;
故答案为:BE=DF.
16.解:如图,∵图中的四边形为正方形,
∴∠ABD=90°,AB=DB,
∴∠ABC+∠DBE=90°,
∵∠ABC+∠CAB=90°,
∴∠CAB=∠DBE,
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS),
∴AC=BE,
∵DE2+BE2=BD2,
∴ED2+AC2=BD2,
∵S1=AC2,S2=DE2,BD2=1,
∴S1+S2=1,
同理可得S3+S4=3,
∴S1+S2+S3+S4=1+3=4.
故答案为4.
三.解答题
17.解:∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM,NC=BC,∠ACM=∠BCN=90°,
∵∠MCN=∠NCM,
∴∠ACN=∠BCM,
在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS),
∴AN=BM.
18.(1)证明:∵四边形ABCD是正方形,
∴∠DCE=90°,
∵∠EFC=3∠E,∠EFC+∠E=90°,
∴4∠E=90°,
∴∠E=22.5°,
又∵AC是正方形对角线,
∠ACB=45°,
∵∠ACB=∠E+∠EAC,
∴∠EAC=22.5°,
∴∠EAC=∠E,
∴AC=EC;
(2)解:设正方形的边长为x,则AC=EC=x,
∵AD∥BC,
∴∠DAF=∠E,
∵∠ADC=∠FDE=90°,
∴x=2+2,
∴正方形的边长为2+2.
19.(1)证明:∵四边形ABCD是正方形,
∴∠BCG=∠DCE=90°,BC=CD,
∵BF⊥DE,
∴∠DFG=∠BCG=90°,
∵∠BGC=∠DGF,
∴∠CBG=∠CDE.
在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS),
∴CG=CE;
(2)解:由(1)△BCG≌△DCE得CG=CE,
又∵BE=BC+CE=4,DG=CD﹣CG=2,
∴BC=3CG=,
在Rt△BCG中,BG===2.
20.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)解:当∠A=45°时,四边形BECD是正方形,
理由:∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
21.解:(1)如图1,
EF=BE+DF,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABM=90°,
又∵BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵∠EAF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=∠MAE=45°=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF,
(2)如图2,
EF=BE+DF,仍然成立,理由如下:
延长CB到M,使得BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠4=180°,
∴∠D=∠4,
又∵AB=AD,BM=DF,
∴△ADF≌△ABM(SAS),
∴AF=AM,∠1=∠2,
∵,
∴∠1+∠3=∠EAF,
∴∠MAE=∠2+∠3=∠EAF,
又∵AE=AE,
∴△EAM≌△EAF(SAS),
∴EF=EM=BE+BM,
又∵BM=DF,
∴EF=EB+DF.
22.证明:如图,将△CBF绕点B逆时针旋转90°,可得△ABN,连接EN,
由旋转的性质可得BN=BF,AN=CF,∠BAN=∠BCF=45°,∠CBF=∠ABN,
∴∠CAN=∠CAB+∠BAN=90°,
∴EN2=AE2+AN2,
∵∠EBF=45°,
∴∠CBF+∠ABE=45°,
∴∠ABE+∠ABN=45°=∠NBE=∠EBF,
在△EBF和△EBN中,
,
∴△EBF≌△EBN(SAS),
∴EF=EN,
∴EF2=AE2+CF2.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
