2021-2022学年湘教版八年级数学下册2.5矩形 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册2.5矩形 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 10:41:40 | ||
图片预览




文档简介
2021-2022学年湘教版八年级数学下册《2-5矩形》同步练习题(附答案)
一.选择题
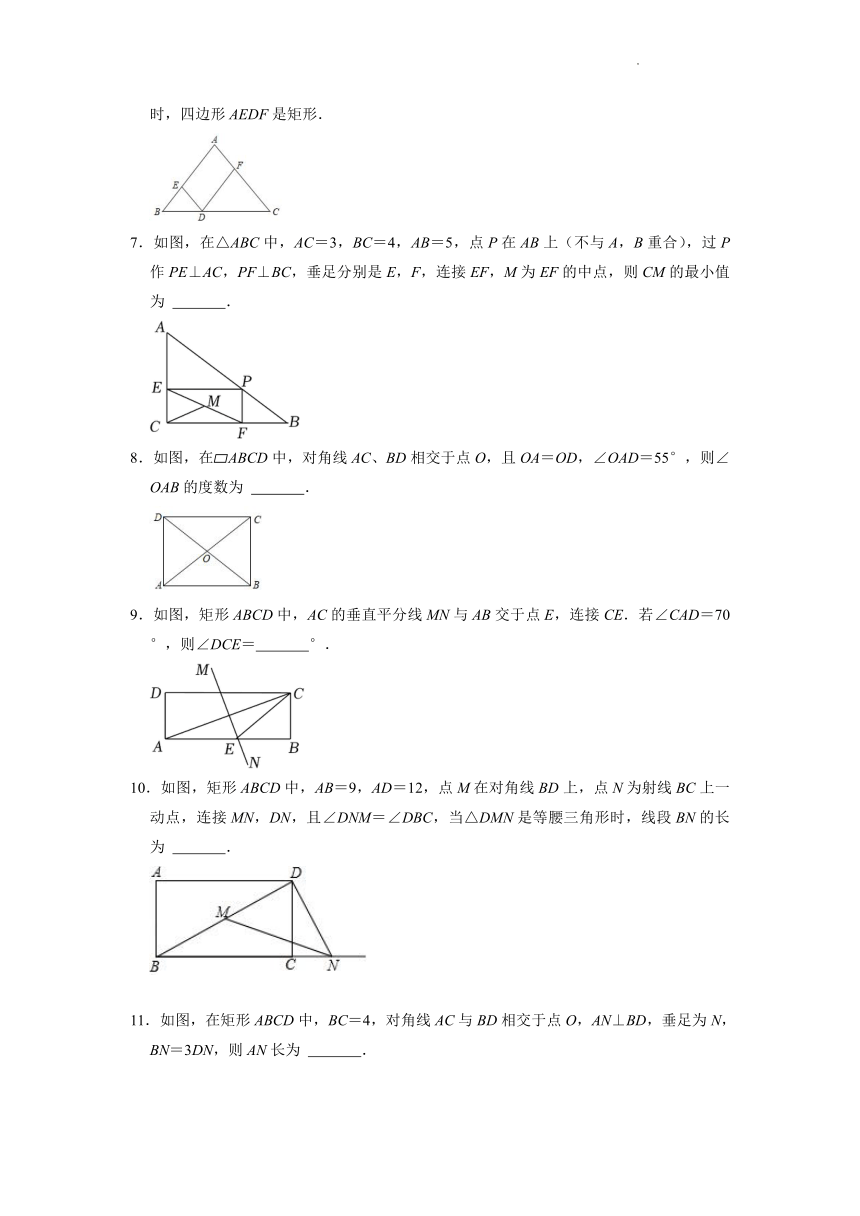
1.如图,O是矩形ABCD的对角线BD的中点,E是AB边的中点.若AB=8,OE=3,则线段OC的长为( )
A.3 B.4 C.5 D.6
2.如图所示,四边形ABCD是矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=5,设AB=x,AD=y,则x2+(y﹣5)2的值为( )
A.10 B.25 C.50 D.75
3.如图,在矩形ABCD中,AB=2,BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点F,EF⊥BD于点F,则OE+EF的值为( )
A. B.2 C. D.2
4.如图,在长方形ABCD中,AB=CD=8cm,BC=12cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,同时,点Q由点C出发,以相同的速度沿CD向点D运动,设点P的运动时间为t秒,当△ABP≌△PCQ时,t的值为( )
A.1或3 B.2 C.2或4 D.1或2
5.矩形具有而平行四边形不一定具有的性质是( )
A.两组对边分别相等 B.对角线相等
C.两组对边分别平行 D.对角线互相平分
二.填空题
6.如图,在△ABC中,AB=AC,点D在BC边上,DF∥AB,DE∥AC,则当∠B= °时,四边形AEDF是矩形.
7.如图,在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A,B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E,F,连接EF,M为EF的中点,则CM的最小值为 .
8.如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为 .
9.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
10.如图,矩形ABCD中,AB=9,AD=12,点M在对角线BD上,点N为射线BC上一动点,连接MN,DN,且∠DNM=∠DBC,当△DMN是等腰三角形时,线段BN的长为 .
11.如图,在矩形ABCD中,BC=4,对角线AC与BD相交于点O,AN⊥BD,垂足为N,BN=3DN,则AN长为 .
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,则∠CAE= .
13.如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G,若G是CD的中点,GE=5,则FO的长是 .
14.如图,在矩形ABCD中,E为边AD延长线上一点,DE=AC,连结BE,BD.若∠CAD=54°,则∠E= 度.
15.在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,与此同时点Q从点C出发,以acm/秒的速度沿CD向点D运动,当点P到达C点或点Q到达D点时,P、Q运动停止,当a= 时,△ABP与△PQC全等.
三.解答题
16.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
17.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AD⊥BD,点E是CD的中点,过点E作EF∥BD,交BC于点F.
(1)求证:四边形OEFB是矩形;
(2)若AD=6,S矩形OEFB=12,求AB的长.
18.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)DF⊥AC,若∠ADF:∠FDC=2:1,则∠BDF的度数是多少?
19.如图,在△ABC中,∠ABC=90°,点O是斜边AC的中点,过点O作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD、DE.
(1)求证:四边形ABCD是矩形;
(2)若BC=3,∠BAC=30°,求DE的长.
20.如图,在 ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连结BE、CE.
(1)求证:四边形BFDE是矩形.
(2)若DE=AB,∠ABC=130°,求∠DEC的度数.
参考答案
一.选择题
1.解:∵四边形ABCD是矩形,
∴∠A=∠BCD=90°,DO=OB,
∵E是AB边的中点,
∴OE是△ADB的中位线,
∴AD=2OE=6,
∵AB=8,
∴BD=,
∴OC=BD=5,
故选:C.
2.解:∵四边形ABCD是矩形,
∴AB=CD=x,AD=BC=y,
∵BD⊥DE,点F是BE的中点,
∴DF=BF=EF=5,
∴CF=5﹣y,
∴DF2=DC2+CF2=x2+(y﹣5)2=25,
故选:B.
3.解:∵AB=2,BC=4,
∴矩形ABCD的面积为8,AC===2,
∴BO=CO=AC=,
∵对角线AC,BD交于点O,
∴△BOC的面积为2,
∵EO⊥AO,EF⊥DO,
∴S△BOC=S△BOE+S△COE,
2=CO×EO+BO×EF,
∴2=××EO+×EF,
∴(EO+EF)=4,
∴EO+EF=,
故选:A.
4.解:当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=8cm,
∴PC=8cm,
∴BP=12﹣8=4(cm),
∴2t=4,解得:t=2,
故选:B.
5.解:矩形的性质有两组对边平行且相等,对角线互相平分且相等,平行四边形的性质有两组对边平行且相等,对角线互相平分,
故选:B.
二.填空题
6.解:当∠B=45°时,四边形AEDF是矩形.
∵DF∥AB,DE∥AC,
∴四边形AEDF是平行四边形,
∵AB=AC,
∴∠B=∠C=45°,
∴∠A=90°,
∴四边形AEDF是矩形.
故答案为45.
7.解:∵AC=3,BC=4,AB=5,
∴AC2+BC2=25=AB2,
∴△ABC是直角三角形且∠ACB=90°,
又∵PE⊥AC,PF⊥BC,
∴四边形CEPF是矩形,
如图,连接CP,则CP=EF,
∵M为EF的中点,∠ECF=90°,
∴Rt△CEF中,CM=EF,
∴CM=CP,
如图,当CP⊥AB时,CP最短,
此时,×AC×BC=×AB×CP,
∴CP==,
∴CM=CP=1.2,即CM的最小值为1.2.
故答案为:1.2.
8.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=55°,
∴∠OAB=∠DAB﹣∠OAD=35°,
故答案为:35°.
9.解:∵MN是AC的垂直平分线,
∴EC=EA,
∴∠ECA=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°﹣70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
故答案为:40.
10.解:∵四边形ABCD是矩形,AB=9,AD=12,
∴BC=12,DC=9,DC⊥BC,
①如图1中,当NM=ND时,
∴∠NDM=∠NMD,
∵∠MND=∠CBD,
∴∠BDN=∠BND,
∴BD=BN==15;
②如图2中,当DM=DN时,
易知M与B重合,此时BC=CN=12,BN=24,
③如图3中,当MN=MD时,
∵MN=MD,
∴∠MND=∠MDN,
∵∠DNM=∠DBC,
∴∠DBC=∠MDN,
∴BN=ND,
设BN=DN=x,
在Rt△DNC中,
∵DN2=CN2+CD2,
∴x2=(12﹣x)2+92,
∴x=,
故答案为15或24或.
11.解:∵四边形ABCD是矩形,BC=AD=4,
∴BO=OD=OA=OC,
∵BN=3DN,
∴ON=DN,
∵AN⊥BD,
∴△OAD是等腰三角形,
∴OA=AD,
∵OA=OD,
∴△OAD是等边三角形,
∴OD=AD=BC=4,
∴AN=,
故答案为:2.
12.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,∠BAD=90°,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵BO=BE,
∴AB=BO=OA,
∴△BAO是等边三角形,
∴∠OAB=60°,
∴∠CAE=∠OAB﹣∠BAE=15°,
故答案为:15°.
13.解:∵矩形ABCD,AB=8,AE=4,
∴∠A=90°,
∴BE=,
∵BE的垂直平分线交BC的延长线于点F,
∴EO=,
∵G是CD的中点,
∴DG=GC,
在△EDG与△FCG中,
∴△EDG≌△FCG,
∴EG=GF=5,
∴EF=10,
∴在Rt△EFO中,OF=.
故答案为:4
14.解:∵四边形ABCD是矩形,
∴AC=BD,
∵DE=AC,
∴BD=DE,
∴∠E=∠DBE,
∵∠BDA=∠CAD=54°,
∴∠E+∠DBE=∠BDA=54°,
∴∠E=27°.
故答案为:27.
15.解:∵四边形ABCD是长方形,
∴∠B=∠C=90°,
有两种情况:①当BP=CQ,AB=PC=6cm时,△ABP≌△PCQ,
此时BP=CQ=10﹣6=4(cm),
∵点P运动的速度是2cm/s,
∴运动的时间是=2(秒),
即2a=4,
解得:a=2;
②当BP=PC,AB=CQ=6cm时,△ABP≌△PQC,
此时BP=PC=10=5(cm),
∵点P运动的速度是2cm/s,
∴运动的时间是2.5秒,
即2.5a=6,
解得:a=2.4;
故答案为:2或2.4.
三.解答题
16.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形;
(2)解:由(1)得:四边形DFBE是矩形,
∴DE=BF,
∵CF平分∠DCB,
∴∠DCF=∠BCF,
∵AB∥CD,
∴∠DCF=∠CFB,
∴∠BCF=∠CFB,
∴BF=BC=5,
∴DE=BF=5,
∴CD=DE+CE=5+3=8.
17.(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AD∥BC,AB∥CD.
∵点E是CD的中点,
∴OE是△BCD的中位线.
∴,OE∥BC.
∵EF∥BD,OE∥BC,
∴四边形OEFB是平行四边形.
∵AD⊥BD,AD∥BC,
∴BC⊥BD,
∴∠CBD=90°.
∴四边形OEFB是矩形.
(2)解:∵,S矩形OEFB=OB×OE=12,
∴OB=4.
∴BD=2OB=8.
∵AD⊥BD,
∴∠ADB=90°,
由勾股定理得,.
即AB的长为10.
18.(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴平行四边形ABCD是矩形;
(2)解:由(1)得:∠ADC=90°,四边形ABCD是矩形,
∵∠ADF:∠FDC=2:1,AC=BD,
∴∠FDC=30°,
∵DF⊥AC,
∴∠DCO=90°﹣30°=60°,
∵AO=CO,BO=DO,
∴OC=OD,
∴∠ODC=∠DCO=60°,
∴∠BDF=∠ODC﹣∠FDC=30°.
19.(1)证明:∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,
∵∠ABC=90°,∠BAC=30°,
∴AC=2BC=6,
∴OA=3,
∵OE⊥AC,
∴∠AOE=90°,
∵∠BAC=30°,
∴OE=OA=,
∴AE=2OE=2,
∴DE===.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴ED∥BF.
∵ED=AD﹣AE,BF=BC﹣CF,AE=CF,
∴ED=BF.
∴四边形BFDE是平行四边形.
∵DF⊥BC,
∴∠DFB=90°.
∴四边形BFDE是矩形.
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,∠ADC=∠ABC=130°,
∵DE=AB,
∴DE=CD,
∴
一.选择题
1.如图,O是矩形ABCD的对角线BD的中点,E是AB边的中点.若AB=8,OE=3,则线段OC的长为( )
A.3 B.4 C.5 D.6
2.如图所示,四边形ABCD是矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=5,设AB=x,AD=y,则x2+(y﹣5)2的值为( )
A.10 B.25 C.50 D.75
3.如图,在矩形ABCD中,AB=2,BC=4,对角线AC,BD相交于点O,OE⊥AC交BC于点F,EF⊥BD于点F,则OE+EF的值为( )
A. B.2 C. D.2
4.如图,在长方形ABCD中,AB=CD=8cm,BC=12cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,同时,点Q由点C出发,以相同的速度沿CD向点D运动,设点P的运动时间为t秒,当△ABP≌△PCQ时,t的值为( )
A.1或3 B.2 C.2或4 D.1或2
5.矩形具有而平行四边形不一定具有的性质是( )
A.两组对边分别相等 B.对角线相等
C.两组对边分别平行 D.对角线互相平分
二.填空题
6.如图,在△ABC中,AB=AC,点D在BC边上,DF∥AB,DE∥AC,则当∠B= °时,四边形AEDF是矩形.
7.如图,在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A,B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E,F,连接EF,M为EF的中点,则CM的最小值为 .
8.如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为 .
9.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
10.如图,矩形ABCD中,AB=9,AD=12,点M在对角线BD上,点N为射线BC上一动点,连接MN,DN,且∠DNM=∠DBC,当△DMN是等腰三角形时,线段BN的长为 .
11.如图,在矩形ABCD中,BC=4,对角线AC与BD相交于点O,AN⊥BD,垂足为N,BN=3DN,则AN长为 .
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AE平分∠BAD交BC于点E,且BO=BE,则∠CAE= .
13.如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G,若G是CD的中点,GE=5,则FO的长是 .
14.如图,在矩形ABCD中,E为边AD延长线上一点,DE=AC,连结BE,BD.若∠CAD=54°,则∠E= 度.
15.在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,与此同时点Q从点C出发,以acm/秒的速度沿CD向点D运动,当点P到达C点或点Q到达D点时,P、Q运动停止,当a= 时,△ABP与△PQC全等.
三.解答题
16.在平行四边形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接DF,CF.
(1)求证:四边形DFBE是矩形;
(2)当CF平分∠DCB时,若CE=3,BC=5,求CD的长.
17.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AD⊥BD,点E是CD的中点,过点E作EF∥BD,交BC于点F.
(1)求证:四边形OEFB是矩形;
(2)若AD=6,S矩形OEFB=12,求AB的长.
18.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)DF⊥AC,若∠ADF:∠FDC=2:1,则∠BDF的度数是多少?
19.如图,在△ABC中,∠ABC=90°,点O是斜边AC的中点,过点O作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD、DE.
(1)求证:四边形ABCD是矩形;
(2)若BC=3,∠BAC=30°,求DE的长.
20.如图,在 ABCD中,过点D作DF⊥BC于点F,点E在边AD上,AE=CF,连结BE、CE.
(1)求证:四边形BFDE是矩形.
(2)若DE=AB,∠ABC=130°,求∠DEC的度数.
参考答案
一.选择题
1.解:∵四边形ABCD是矩形,
∴∠A=∠BCD=90°,DO=OB,
∵E是AB边的中点,
∴OE是△ADB的中位线,
∴AD=2OE=6,
∵AB=8,
∴BD=,
∴OC=BD=5,
故选:C.
2.解:∵四边形ABCD是矩形,
∴AB=CD=x,AD=BC=y,
∵BD⊥DE,点F是BE的中点,
∴DF=BF=EF=5,
∴CF=5﹣y,
∴DF2=DC2+CF2=x2+(y﹣5)2=25,
故选:B.
3.解:∵AB=2,BC=4,
∴矩形ABCD的面积为8,AC===2,
∴BO=CO=AC=,
∵对角线AC,BD交于点O,
∴△BOC的面积为2,
∵EO⊥AO,EF⊥DO,
∴S△BOC=S△BOE+S△COE,
2=CO×EO+BO×EF,
∴2=××EO+×EF,
∴(EO+EF)=4,
∴EO+EF=,
故选:A.
4.解:当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=8cm,
∴PC=8cm,
∴BP=12﹣8=4(cm),
∴2t=4,解得:t=2,
故选:B.
5.解:矩形的性质有两组对边平行且相等,对角线互相平分且相等,平行四边形的性质有两组对边平行且相等,对角线互相平分,
故选:B.
二.填空题
6.解:当∠B=45°时,四边形AEDF是矩形.
∵DF∥AB,DE∥AC,
∴四边形AEDF是平行四边形,
∵AB=AC,
∴∠B=∠C=45°,
∴∠A=90°,
∴四边形AEDF是矩形.
故答案为45.
7.解:∵AC=3,BC=4,AB=5,
∴AC2+BC2=25=AB2,
∴△ABC是直角三角形且∠ACB=90°,
又∵PE⊥AC,PF⊥BC,
∴四边形CEPF是矩形,
如图,连接CP,则CP=EF,
∵M为EF的中点,∠ECF=90°,
∴Rt△CEF中,CM=EF,
∴CM=CP,
如图,当CP⊥AB时,CP最短,
此时,×AC×BC=×AB×CP,
∴CP==,
∴CM=CP=1.2,即CM的最小值为1.2.
故答案为:1.2.
8.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=55°,
∴∠OAB=∠DAB﹣∠OAD=35°,
故答案为:35°.
9.解:∵MN是AC的垂直平分线,
∴EC=EA,
∴∠ECA=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°﹣70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
故答案为:40.
10.解:∵四边形ABCD是矩形,AB=9,AD=12,
∴BC=12,DC=9,DC⊥BC,
①如图1中,当NM=ND时,
∴∠NDM=∠NMD,
∵∠MND=∠CBD,
∴∠BDN=∠BND,
∴BD=BN==15;
②如图2中,当DM=DN时,
易知M与B重合,此时BC=CN=12,BN=24,
③如图3中,当MN=MD时,
∵MN=MD,
∴∠MND=∠MDN,
∵∠DNM=∠DBC,
∴∠DBC=∠MDN,
∴BN=ND,
设BN=DN=x,
在Rt△DNC中,
∵DN2=CN2+CD2,
∴x2=(12﹣x)2+92,
∴x=,
故答案为15或24或.
11.解:∵四边形ABCD是矩形,BC=AD=4,
∴BO=OD=OA=OC,
∵BN=3DN,
∴ON=DN,
∵AN⊥BD,
∴△OAD是等腰三角形,
∴OA=AD,
∵OA=OD,
∴△OAD是等边三角形,
∴OD=AD=BC=4,
∴AN=,
故答案为:2.
12.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,∠BAD=90°,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵BO=BE,
∴AB=BO=OA,
∴△BAO是等边三角形,
∴∠OAB=60°,
∴∠CAE=∠OAB﹣∠BAE=15°,
故答案为:15°.
13.解:∵矩形ABCD,AB=8,AE=4,
∴∠A=90°,
∴BE=,
∵BE的垂直平分线交BC的延长线于点F,
∴EO=,
∵G是CD的中点,
∴DG=GC,
在△EDG与△FCG中,
∴△EDG≌△FCG,
∴EG=GF=5,
∴EF=10,
∴在Rt△EFO中,OF=.
故答案为:4
14.解:∵四边形ABCD是矩形,
∴AC=BD,
∵DE=AC,
∴BD=DE,
∴∠E=∠DBE,
∵∠BDA=∠CAD=54°,
∴∠E+∠DBE=∠BDA=54°,
∴∠E=27°.
故答案为:27.
15.解:∵四边形ABCD是长方形,
∴∠B=∠C=90°,
有两种情况:①当BP=CQ,AB=PC=6cm时,△ABP≌△PCQ,
此时BP=CQ=10﹣6=4(cm),
∵点P运动的速度是2cm/s,
∴运动的时间是=2(秒),
即2a=4,
解得:a=2;
②当BP=PC,AB=CQ=6cm时,△ABP≌△PQC,
此时BP=PC=10=5(cm),
∵点P运动的速度是2cm/s,
∴运动的时间是2.5秒,
即2.5a=6,
解得:a=2.4;
故答案为:2或2.4.
三.解答题
16.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形DFBE是矩形;
(2)解:由(1)得:四边形DFBE是矩形,
∴DE=BF,
∵CF平分∠DCB,
∴∠DCF=∠BCF,
∵AB∥CD,
∴∠DCF=∠CFB,
∴∠BCF=∠CFB,
∴BF=BC=5,
∴DE=BF=5,
∴CD=DE+CE=5+3=8.
17.(1)证明:∵四边形ABCD是平行四边形,
∴BO=DO,AD∥BC,AB∥CD.
∵点E是CD的中点,
∴OE是△BCD的中位线.
∴,OE∥BC.
∵EF∥BD,OE∥BC,
∴四边形OEFB是平行四边形.
∵AD⊥BD,AD∥BC,
∴BC⊥BD,
∴∠CBD=90°.
∴四边形OEFB是矩形.
(2)解:∵,S矩形OEFB=OB×OE=12,
∴OB=4.
∴BD=2OB=8.
∵AD⊥BD,
∴∠ADB=90°,
由勾股定理得,.
即AB的长为10.
18.(1)证明:∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴平行四边形ABCD是矩形;
(2)解:由(1)得:∠ADC=90°,四边形ABCD是矩形,
∵∠ADF:∠FDC=2:1,AC=BD,
∴∠FDC=30°,
∵DF⊥AC,
∴∠DCO=90°﹣30°=60°,
∵AO=CO,BO=DO,
∴OC=OD,
∴∠ODC=∠DCO=60°,
∴∠BDF=∠ODC﹣∠FDC=30°.
19.(1)证明:∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,
∵∠ABC=90°,∠BAC=30°,
∴AC=2BC=6,
∴OA=3,
∵OE⊥AC,
∴∠AOE=90°,
∵∠BAC=30°,
∴OE=OA=,
∴AE=2OE=2,
∴DE===.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴ED∥BF.
∵ED=AD﹣AE,BF=BC﹣CF,AE=CF,
∴ED=BF.
∴四边形BFDE是平行四边形.
∵DF⊥BC,
∴∠DFB=90°.
∴四边形BFDE是矩形.
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,∠ADC=∠ABC=130°,
∵DE=AB,
∴DE=CD,
∴
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
