第18章 平行四边形 单元测试卷(含答案)
文档属性
| 名称 | 第18章 平行四边形 单元测试卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 215.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-02 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
八年级数学单元测试卷
(平行四边形)
题 号 一 二 三 四 五 六 总分
得 分
一、选择题(本大题共6小题,每小题3分,共18分)
1. 矩形具有而一般的平行四边形不一定具有的特征( ).
A. 对角相等 B.对角线互相平分 C.对角线相等 D.对边相等
2. 已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( ).
3. 能判定四边形ABCD为平行四边形的题设是 ( ).
A. AB∥CD,AD=BC B.AB=CD,AD=BC
C.∠A=∠B,∠C=∠D D.AB=AD,CB=CD
4.顺次连接矩形四边中点得到的四边形一定是( ).
A.菱形 B.矩形 C. 正方形 D.平行四边形
5.如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是( ).
6.如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为( ).
A.3 B.4 C.5 D.6
二、填空题(本大题共6小题,每小题3分,共18分)
7.正方形共有 条对称轴.
8.在平行四边形ABCD中,∠C=∠B+∠D,则∠A=_______度.
9.如图,平行四边形ABCD的周长是18cm,对角线AC,BD相交于点O. 若△AOD与△AOB的周长之差是5cm,则边AB的长是 cm .
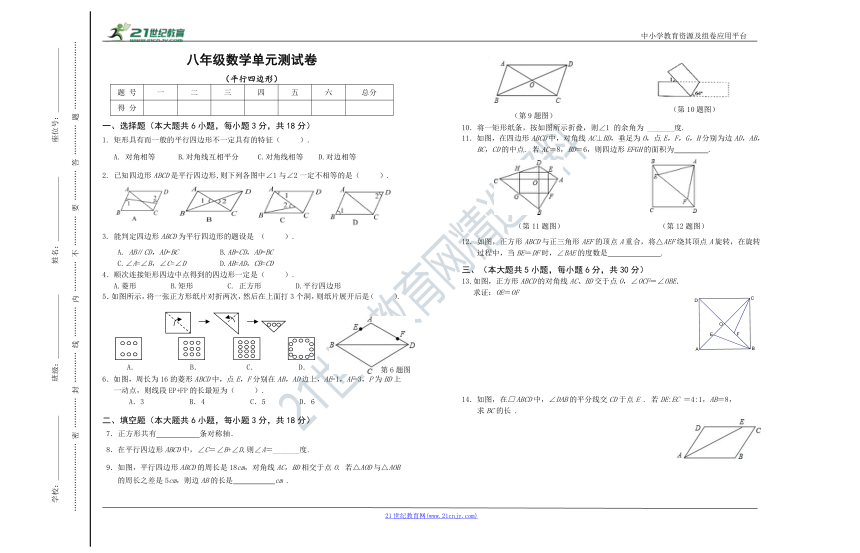
(第9题图)
10.将一矩形纸条,按如图所示折叠,则∠1 的余角为 _______度.
11.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点. 若AC=8,BD=6,则四边形EFGH的面积为 .
(第11题图) (第12题图)
12.如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的度数是 .
三、(本大题共5小题,每小题6分,共30分)
13.如图,正方形ABCD的对角线AC、BD交于点O,∠OCF=∠OBE.
求证:OE=OF
14.如图,在□ABCD中,∠DAB的平分线交CD于点E . 若DE:EC =4:1,AB=8,
求BC的长 .
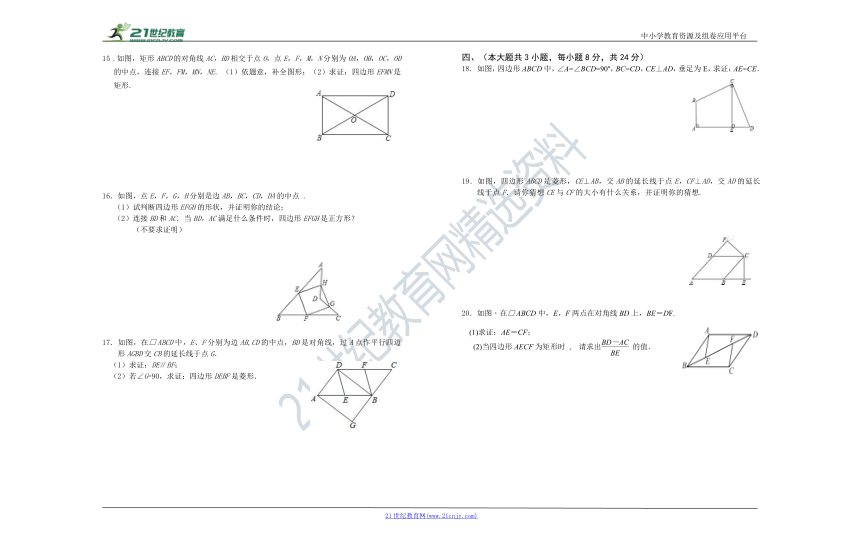
15 .如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.(1)依题意,补全图形;(2)求证:四边形EFMN是矩形.
16.如图,点E,F,G,H分别是边AB,BC,CD,DA的中点 .
(1)试判断四边形EFGH的形状,并证明你的结论;
(2)连接BD和AC.当BD,AC满足什么条件时,四边形EFGH是正方形?
(不要求证明)
17.如图,在□ABCD中,E、F分别为边AB,CD的中点,BD是对角线,过A点作平行四边形AGBD交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
四、(本大题共3小题,每小题8分,共24分)
18. 如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
19.如图,四边形ABCD是菱形,CE⊥AB,交AB的延长线于点E,CF⊥AD,交AD的延长线于点F.请你猜想CE与CF的大小有什么关系,并证明你的猜想.
20.如图,在□ABCD中,E,F两点在对角线BD上,BE=DF.
(1)求证:AE=CF;
(2)当四边形AECF为矩形时 , 请求出 的值.
五、(本大题共2小题,每小题9分,共18分)
21.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,F在DE的延长线上,且AF=CE=AE .
(1)求证:四边形ACEF是平行四边形.
(2)当∠B满足什么条件时,四边形ACEF是菱形?请说明理由.
22.如图,在矩形ABCD中,E,F分别是AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC相交于点O ,且BE=BF,∠BEF=2∠BAC .
(1)求证:OE=OF;
(2)若BC=3,求AB的长.
六、(本大题共12分)
23.在图1、图2、图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM⊥直线AB于点E,PN⊥直线BC于点F.
(1)如图1,当点P与点O重合时,OE与OF的数量关系为 .
(2)如图2,当点P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系,并对你的猜想结果给予证明.
(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为 ,位置关系为 .
O
八年级数学单元测试卷
(平行四边形)参考答案
1.C 2.C 3.B 4.A 5.D 6 .B
7.4 8.120 9.2 10.38 11.12
12.15°或165° 13.略 14. BC=6.4 15.略
16.(1)平行四边形; (2)当BD=AC且BD⊥AC时,四边形EFGH是正方形
17.略 18. 过点B作BF⊥CE于点F,证△BCF≌△CDE 19. CE = CF
20. (1)由SAS证△ABE≌△CDF即可 (2)连接CE,AF,AC. ∵四边形AECF是矩形,
∴AC=EF,∴====2
21.(1)略;(2)当∠B =30°时,四边形ACEF是菱形
22.(1)略;(2)AB=9.
23.(1)OE=OF;(2)OE=OF , OE ⊥ OF ; (3) OE=OF, OE ⊥ OF
1学校: 班级: 姓名: 座位号: 1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
A.
B.
C.
D.
第6题图
(第10题图)
1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级数学单元测试卷
(平行四边形)
题 号 一 二 三 四 五 六 总分
得 分
一、选择题(本大题共6小题,每小题3分,共18分)
1. 矩形具有而一般的平行四边形不一定具有的特征( ).
A. 对角相等 B.对角线互相平分 C.对角线相等 D.对边相等
2. 已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( ).
3. 能判定四边形ABCD为平行四边形的题设是 ( ).
A. AB∥CD,AD=BC B.AB=CD,AD=BC
C.∠A=∠B,∠C=∠D D.AB=AD,CB=CD
4.顺次连接矩形四边中点得到的四边形一定是( ).
A.菱形 B.矩形 C. 正方形 D.平行四边形
5.如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是( ).
6.如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD上一动点,则线段EP+FP的长最短为( ).
A.3 B.4 C.5 D.6
二、填空题(本大题共6小题,每小题3分,共18分)
7.正方形共有 条对称轴.
8.在平行四边形ABCD中,∠C=∠B+∠D,则∠A=_______度.
9.如图,平行四边形ABCD的周长是18cm,对角线AC,BD相交于点O. 若△AOD与△AOB的周长之差是5cm,则边AB的长是 cm .
(第9题图)
10.将一矩形纸条,按如图所示折叠,则∠1 的余角为 _______度.
11.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点. 若AC=8,BD=6,则四边形EFGH的面积为 .
(第11题图) (第12题图)
12.如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的度数是 .
三、(本大题共5小题,每小题6分,共30分)
13.如图,正方形ABCD的对角线AC、BD交于点O,∠OCF=∠OBE.
求证:OE=OF
14.如图,在□ABCD中,∠DAB的平分线交CD于点E . 若DE:EC =4:1,AB=8,
求BC的长 .
15 .如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.(1)依题意,补全图形;(2)求证:四边形EFMN是矩形.
16.如图,点E,F,G,H分别是边AB,BC,CD,DA的中点 .
(1)试判断四边形EFGH的形状,并证明你的结论;
(2)连接BD和AC.当BD,AC满足什么条件时,四边形EFGH是正方形?
(不要求证明)
17.如图,在□ABCD中,E、F分别为边AB,CD的中点,BD是对角线,过A点作平行四边形AGBD交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
四、(本大题共3小题,每小题8分,共24分)
18. 如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
19.如图,四边形ABCD是菱形,CE⊥AB,交AB的延长线于点E,CF⊥AD,交AD的延长线于点F.请你猜想CE与CF的大小有什么关系,并证明你的猜想.
20.如图,在□ABCD中,E,F两点在对角线BD上,BE=DF.
(1)求证:AE=CF;
(2)当四边形AECF为矩形时 , 请求出 的值.
五、(本大题共2小题,每小题9分,共18分)
21.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,F在DE的延长线上,且AF=CE=AE .
(1)求证:四边形ACEF是平行四边形.
(2)当∠B满足什么条件时,四边形ACEF是菱形?请说明理由.
22.如图,在矩形ABCD中,E,F分别是AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC相交于点O ,且BE=BF,∠BEF=2∠BAC .
(1)求证:OE=OF;
(2)若BC=3,求AB的长.
六、(本大题共12分)
23.在图1、图2、图3中,点O是正方形ABCD对角线AC的中点,△MPN为直角三角形,∠MPN=90°.正方形ABCD保持不动,△MPN沿射线AC向右平移,平移过程中P点始终在射线AC上,且保持PM⊥直线AB于点E,PN⊥直线BC于点F.
(1)如图1,当点P与点O重合时,OE与OF的数量关系为 .
(2)如图2,当点P在线段OC上时,猜想OE与OF有怎样的数量关系与位置关系,并对你的猜想结果给予证明.
(3)如图3,当点P在AC的延长线上时,OE与OF的数量关系为 ,位置关系为 .
O
八年级数学单元测试卷
(平行四边形)参考答案
1.C 2.C 3.B 4.A 5.D 6 .B
7.4 8.120 9.2 10.38 11.12
12.15°或165° 13.略 14. BC=6.4 15.略
16.(1)平行四边形; (2)当BD=AC且BD⊥AC时,四边形EFGH是正方形
17.略 18. 过点B作BF⊥CE于点F,证△BCF≌△CDE 19. CE = CF
20. (1)由SAS证△ABE≌△CDF即可 (2)连接CE,AF,AC. ∵四边形AECF是矩形,
∴AC=EF,∴====2
21.(1)略;(2)当∠B =30°时,四边形ACEF是菱形
22.(1)略;(2)AB=9.
23.(1)OE=OF;(2)OE=OF , OE ⊥ OF ; (3) OE=OF, OE ⊥ OF
1学校: 班级: 姓名: 座位号: 1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
A.
B.
C.
D.
第6题图
(第10题图)
1
……………………… 密 ………… 封 ………… 线 ………… 内 ………… 不 ………… 要 ………… 答 ………… 题 ………………………
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
