北师大版数学八年级下册 4.1 因式分解 课件 (共20张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 4.1 因式分解 课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 267.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 11:11:49 | ||
图片预览







文档简介
(共20张PPT)
4.1 因式分解
第四章 因式分解
学习目标
1.解掌握因式分解的意义,会判断一个变形是否为因式分解.(重点)
2.理解因式分解与整式乘法之间的联系与区别.(难点)
导入新课
复习引入
问题1:21能被哪些数整除?
1,3,7,21.
问题2:你是怎样想到的?
因为21=1×21=3×7.
思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
可以.
因式分解的概念
一
讲授新课
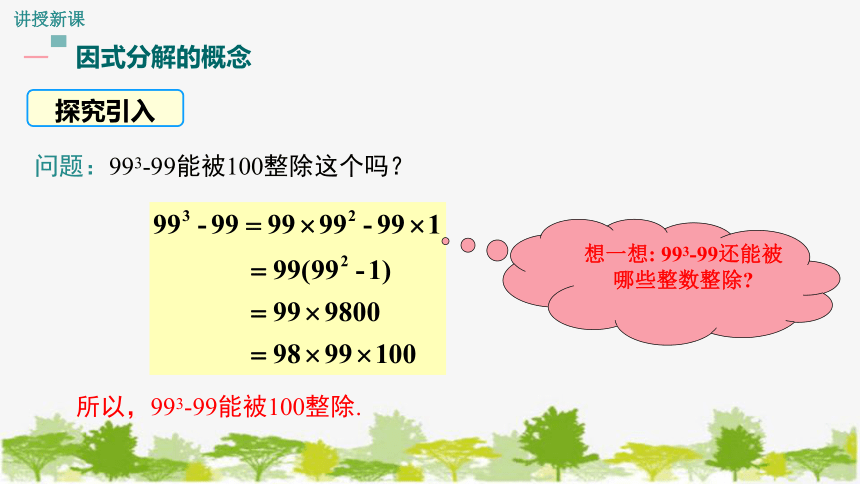
问题:993-99能被100整除这个吗?
所以,993-99能被100整除.
想一想: 993-99还能被哪些整数整除
探究引入
问题探究
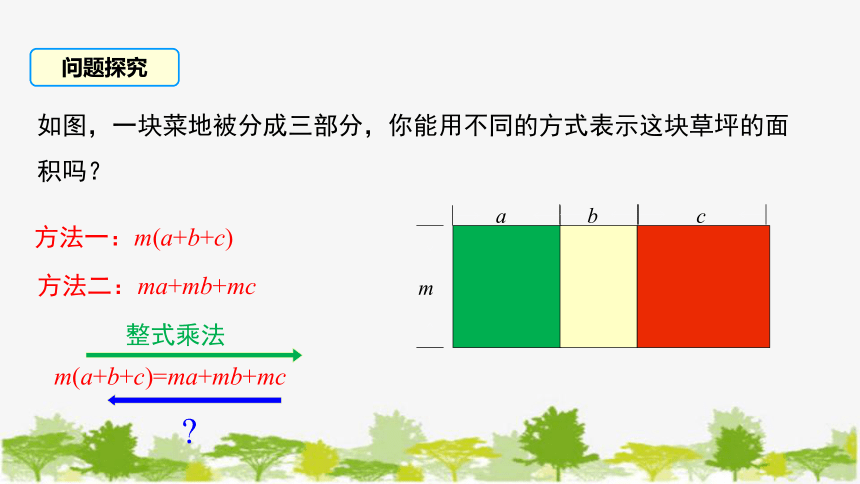
如图,一块菜地被分成三部分,你能用不同的方式表示这块草坪的面积吗?
a
b
c
m
方法一:m(a+b+c)
方法二:ma+mb+mc
m(a+b+c)=ma+mb+mc
整式乘法
完成下列题目:
x(x-2)=_______
(x+y)(x-y)=_______
(x+1)2=________
x2-2x
x2-y2
x2+2x+1
根据左空,解决下列问题:
x2-2x=( )( )
x2-y2=( )( )
x2+2x+1=( )2
x
x-2
x+y
x-y
x+1
做一做
联系:左右两式是同一多项式的不同表现形式.
区别:左边一栏是多项式的乘法,右边一栏是把多项式化成了几个整式的积,他们的运算是相反的.
问题2:右边一栏表示的正是多项式的因式分解,你能根据我们的分析说出什么是因式分解吗?
问题1:观察同一行中,左右两边的等式有什么区别和联系?
总结归纳
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解,也可称为分解因式.
其中,每个整式都叫做这个多项式的因式.
判断下列各式从左到右的变形中,是否为因式分解:
辩一辩
A. x(a﹣b)=ax﹣bx
B. x2﹣1+y2=(x﹣1)(x+1)+y2
C. y2﹣1=(y+1)(y﹣1)
D. ax+by+c=x(a+b)+c
E. 2a3b=a2 2ab
F. (x+3)(x﹣3)=x2﹣9
√
×
×
×
×
×
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式. (3)右边的因式全是整式.
做一做
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
(1) 3x(x-1)= __,
(2) m(a+b+c) = ______ ,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
由a(a+1)(a-1)得到a3-a的变形是整式乘法,
由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
因式分解与整式乘法的关系
二
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,右边是几个整式的乘积
想一想:整式乘法与因式分解有什么关系?
是互为相反的变形,即
例 若多项式x2+ax+b分解因式的结果为
a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3)
=ax2+ax-6a.
∴a=1,b=﹣6a=﹣6.
典例精析
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数对应比较即可.
下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )
A.x2﹣y2 B.﹣x2+y2
C.x2+y2 D.﹣x2﹣y2
B
练一练
当堂练习
2. 下列从左到右的变形中,是因式分解的有______ .
①24x2y=4x 6xy ②(x+5)(x﹣5)=x2﹣25 ③x2+2x﹣3=(x+3)(x﹣1)
④9x2﹣6x+1=3x(x﹣2)+1 ⑤x2+1=x(x+ )
⑥3xn+2+27xn=3xn( x2+9)
1. 下列各式中从左到右的变形属于分解因式的是
( )
A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2
C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ )
C
③⑥
3. 把多项式x2+4mx+5因式分解得(x+5)(x+n),则m+n的值为 .
解析:由题意可得
x2+4mx+5=(x+5)(x+n)
=x2+(n+5)x+5n,
5n=5,4m=n+5.
解得n=1,m= ,
m+n=1+ = .
4. 20042+2004能被2005整除吗
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除
5. 若多项式x4+mx3+nx﹣16含有因式(x﹣2)和(x﹣1),
求mn的值.
解:∵x4+mx3+nx﹣16的最高次数是4,
∴可设x4+mx3+nx﹣16=(x-1)(x-2)(x2+ax+b),
则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b
比较系数得 2b=-16,b-3a+2=0,a-3=m,2a-3b=n
解得a=-2,b=-8,m=-5,n=20.
∴mn=﹣5×20=﹣100.
6. 甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),求a+b的值.
解:分解因式甲看错了b,但a是正确的,
其分解结果为x2+ax+b=(x+2)(x+4)=x2+6x+8,
∴a=6,
同理,乙看错了a,但b是正确的,
分解结果为x2+ax+b=(x+1)(x+9)=x2+10x+9,
∴b=9,
∴a+b=15.
课堂小结
因式分解
定义:把一个多项式化成几个整式的_____的形式,叫做因式分解,也可称为___________.
其中,每个整式叫做这个多项式的_______.
与多项式乘法运算的关系
的变形过程.
前者是把一个多项式化为几个整式的_____,后者是把几个整式的______化为一个_________.
积
分解因式
因式
相反
多项式
乘积
乘积
4.1 因式分解
第四章 因式分解
学习目标
1.解掌握因式分解的意义,会判断一个变形是否为因式分解.(重点)
2.理解因式分解与整式乘法之间的联系与区别.(难点)
导入新课
复习引入
问题1:21能被哪些数整除?
1,3,7,21.
问题2:你是怎样想到的?
因为21=1×21=3×7.
思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
可以.
因式分解的概念
一
讲授新课
问题:993-99能被100整除这个吗?
所以,993-99能被100整除.
想一想: 993-99还能被哪些整数整除
探究引入
问题探究
如图,一块菜地被分成三部分,你能用不同的方式表示这块草坪的面积吗?
a
b
c
m
方法一:m(a+b+c)
方法二:ma+mb+mc
m(a+b+c)=ma+mb+mc
整式乘法
完成下列题目:
x(x-2)=_______
(x+y)(x-y)=_______
(x+1)2=________
x2-2x
x2-y2
x2+2x+1
根据左空,解决下列问题:
x2-2x=( )( )
x2-y2=( )( )
x2+2x+1=( )2
x
x-2
x+y
x-y
x+1
做一做
联系:左右两式是同一多项式的不同表现形式.
区别:左边一栏是多项式的乘法,右边一栏是把多项式化成了几个整式的积,他们的运算是相反的.
问题2:右边一栏表示的正是多项式的因式分解,你能根据我们的分析说出什么是因式分解吗?
问题1:观察同一行中,左右两边的等式有什么区别和联系?
总结归纳
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解,也可称为分解因式.
其中,每个整式都叫做这个多项式的因式.
判断下列各式从左到右的变形中,是否为因式分解:
辩一辩
A. x(a﹣b)=ax﹣bx
B. x2﹣1+y2=(x﹣1)(x+1)+y2
C. y2﹣1=(y+1)(y﹣1)
D. ax+by+c=x(a+b)+c
E. 2a3b=a2 2ab
F. (x+3)(x﹣3)=x2﹣9
√
×
×
×
×
×
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式. (3)右边的因式全是整式.
做一做
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
(1) 3x(x-1)= __,
(2) m(a+b+c) = ______ ,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
由a(a+1)(a-1)得到a3-a的变形是整式乘法,
由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
因式分解与整式乘法的关系
二
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,右边是几个整式的乘积
想一想:整式乘法与因式分解有什么关系?
是互为相反的变形,即
例 若多项式x2+ax+b分解因式的结果为
a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3)
=ax2+ax-6a.
∴a=1,b=﹣6a=﹣6.
典例精析
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数对应比较即可.
下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )
A.x2﹣y2 B.﹣x2+y2
C.x2+y2 D.﹣x2﹣y2
B
练一练
当堂练习
2. 下列从左到右的变形中,是因式分解的有______ .
①24x2y=4x 6xy ②(x+5)(x﹣5)=x2﹣25 ③x2+2x﹣3=(x+3)(x﹣1)
④9x2﹣6x+1=3x(x﹣2)+1 ⑤x2+1=x(x+ )
⑥3xn+2+27xn=3xn( x2+9)
1. 下列各式中从左到右的变形属于分解因式的是
( )
A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2
C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ )
C
③⑥
3. 把多项式x2+4mx+5因式分解得(x+5)(x+n),则m+n的值为 .
解析:由题意可得
x2+4mx+5=(x+5)(x+n)
=x2+(n+5)x+5n,
5n=5,4m=n+5.
解得n=1,m= ,
m+n=1+ = .
4. 20042+2004能被2005整除吗
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除
5. 若多项式x4+mx3+nx﹣16含有因式(x﹣2)和(x﹣1),
求mn的值.
解:∵x4+mx3+nx﹣16的最高次数是4,
∴可设x4+mx3+nx﹣16=(x-1)(x-2)(x2+ax+b),
则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b
比较系数得 2b=-16,b-3a+2=0,a-3=m,2a-3b=n
解得a=-2,b=-8,m=-5,n=20.
∴mn=﹣5×20=﹣100.
6. 甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),求a+b的值.
解:分解因式甲看错了b,但a是正确的,
其分解结果为x2+ax+b=(x+2)(x+4)=x2+6x+8,
∴a=6,
同理,乙看错了a,但b是正确的,
分解结果为x2+ax+b=(x+1)(x+9)=x2+10x+9,
∴b=9,
∴a+b=15.
课堂小结
因式分解
定义:把一个多项式化成几个整式的_____的形式,叫做因式分解,也可称为___________.
其中,每个整式叫做这个多项式的_______.
与多项式乘法运算的关系
的变形过程.
前者是把一个多项式化为几个整式的_____,后者是把几个整式的______化为一个_________.
积
分解因式
因式
相反
多项式
乘积
乘积
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
