人教版数学七年级下册5.2.2平行线的判定 课件 (共14张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.2.2平行线的判定 课件 (共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 11:16:59 | ||
图片预览

文档简介
(共14张PPT)
数学 七年级下册 人教版
5.2 平行线及其判定
第五章 相交线与平行线
5.2.2 平行线的判定
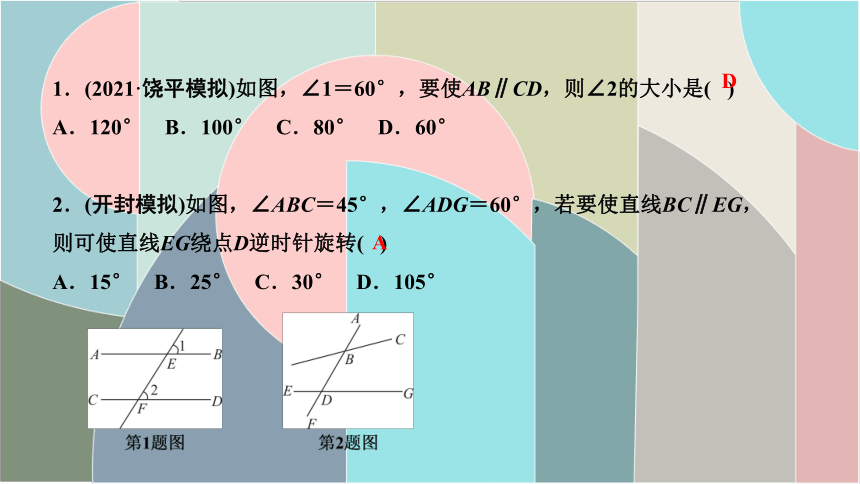
1.(2021·饶平模拟)如图,∠1=60°,要使AB∥CD,则∠2的大小是( )
A.120° B.100° C.80° D.60°
2.(开封模拟)如图,∠ABC=45°,∠ADG=60°,若要使直线BC∥EG,
则可使直线EG绕点D逆时针旋转( )
A.15° B.25° C.30° D.105°
D
A
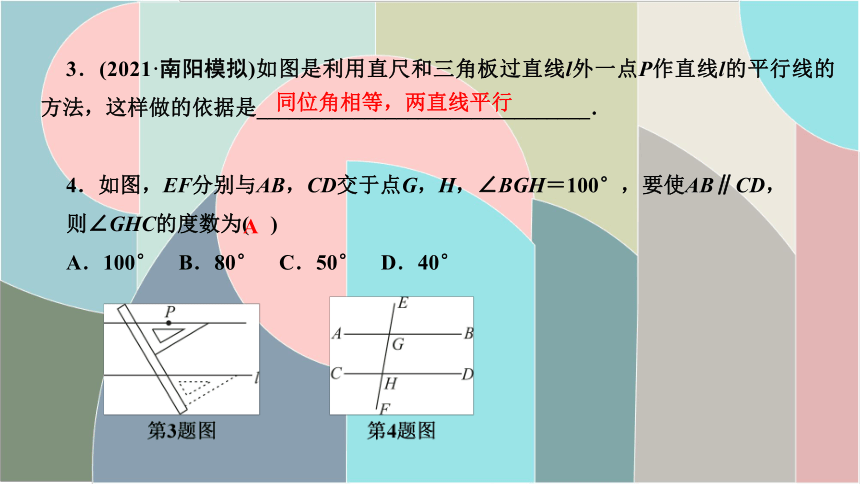
3.(2021·南阳模拟)如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是_______________________________.
4.如图,EF分别与AB,CD交于点G,H,∠BGH=100°,要使AB∥CD,
则∠GHC的度数为( )
A.100° B.80° C.50° D.40°
同位角相等,两直线平行
A
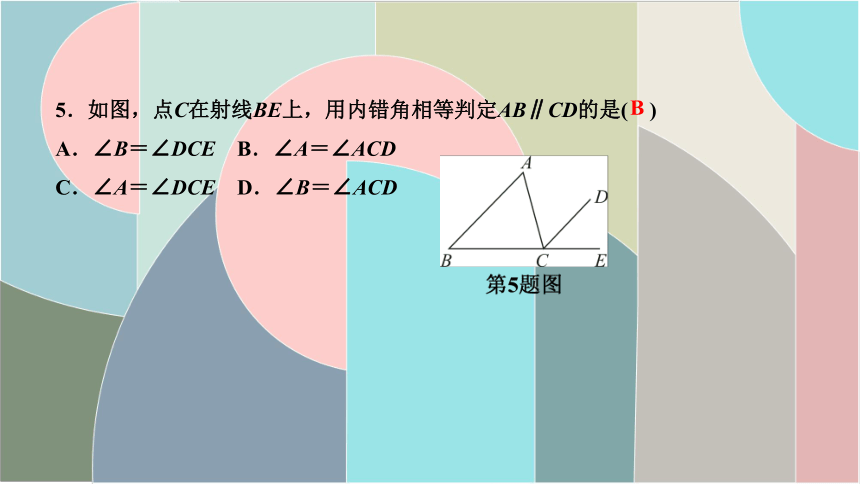
5.如图,点C在射线BE上,用内错角相等判定AB∥CD的是( )
A.∠B=∠DCE B.∠A=∠ACD
C.∠A=∠DCE D.∠B=∠ACD
B
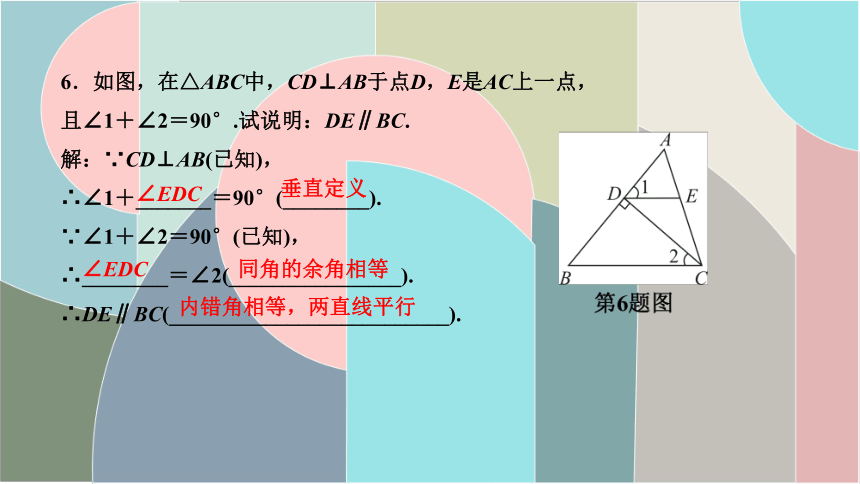
6.如图,在△ABC中,CD⊥AB于点D,E是AC上一点,
且∠1+∠2=90°.试说明:DE∥BC.
解:∵CD⊥AB(已知),
∴∠1+_______=90°(________).
∵∠1+∠2=90°(已知),
∴________=∠2(________________).
∴DE∥BC(__________________________).
∠EDC
垂直定义
∠EDC
同角的余角相等
内错角相等,两直线平行
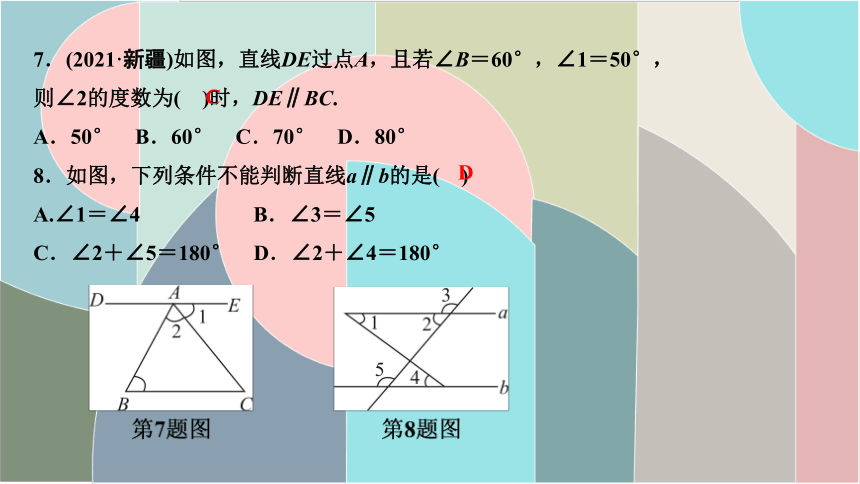
7.(2021·新疆)如图,直线DE过点A,且若∠B=60°,∠1=50°,
则∠2的度数为( )时,DE∥BC.
A.50° B.60° C.70° D.80°
8.如图,下列条件不能判断直线a∥b的是( )
A.∠1=∠4 B.∠3=∠5
C.∠2+∠5=180° D.∠2+∠4=180°
C
D
9.(淄博中考)如图是一个由4条线段构成的“鱼”形图案,
其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.理由:∵∠1=50°,∠2=50°,∴∠1=∠2,
∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC
10.在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线( )
A.互相垂直 B.互相平行
C.相交 D.相等
11.(2021·永城期末)如图,点E在AC的延长线上,
下列条件中不能判定BD∥AE的是( )
A.∠1=∠2 B.∠3=∠4
C.∠D=∠DCE D.∠A+∠ABD=180°
B
A
12.如图,下列条件:①∠1=∠2;②∠A+∠C=180°;③∠B+∠2=180°且CD∥EF;④∠2+∠3=180°且AB∥EF.其中能判断AB∥CD的有______(填序号).
②③④
13.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°,试说明:AB∥CD.
解:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=∠ACD+∠ACB=70°+60°=130°.
∵∠ABC=50°,∴∠BCD+∠ABC=130°+50°=180°,∴AB∥CD
14.如图,直线EF分别与直线AB,CD相交于点P,Q,PG平分∠APQ,
QH平分∠DQP,且∠1=∠2,找出图中的平行线,并说明理由.
15.如图,直线AB,CD交于点O,OE,OF分别平分∠AOD和∠BOD,
已知∠1+∠2=90°,且∠1∶∠3=1∶8.
(1)求∠AOF的度数;
(2)试说明:AB∥EF.
16.如图,∠B=45°,∠BED=75°,∠D=30°,
猜想AB与CD有怎样的位置关系?并说明理由.
解:AB∥CD.理由:在∠BED内作∠BEF=45°,
则∠B=∠BEF=45°,∴AB∥EF.
∵∠BED=75°,∴∠FED=∠BED-∠BEF=75°-45°=30°,
∴∠FED=∠D=30°,∴EF∥CD,∴AB∥CD
数学 七年级下册 人教版
5.2 平行线及其判定
第五章 相交线与平行线
5.2.2 平行线的判定
1.(2021·饶平模拟)如图,∠1=60°,要使AB∥CD,则∠2的大小是( )
A.120° B.100° C.80° D.60°
2.(开封模拟)如图,∠ABC=45°,∠ADG=60°,若要使直线BC∥EG,
则可使直线EG绕点D逆时针旋转( )
A.15° B.25° C.30° D.105°
D
A
3.(2021·南阳模拟)如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是_______________________________.
4.如图,EF分别与AB,CD交于点G,H,∠BGH=100°,要使AB∥CD,
则∠GHC的度数为( )
A.100° B.80° C.50° D.40°
同位角相等,两直线平行
A
5.如图,点C在射线BE上,用内错角相等判定AB∥CD的是( )
A.∠B=∠DCE B.∠A=∠ACD
C.∠A=∠DCE D.∠B=∠ACD
B
6.如图,在△ABC中,CD⊥AB于点D,E是AC上一点,
且∠1+∠2=90°.试说明:DE∥BC.
解:∵CD⊥AB(已知),
∴∠1+_______=90°(________).
∵∠1+∠2=90°(已知),
∴________=∠2(________________).
∴DE∥BC(__________________________).
∠EDC
垂直定义
∠EDC
同角的余角相等
内错角相等,两直线平行
7.(2021·新疆)如图,直线DE过点A,且若∠B=60°,∠1=50°,
则∠2的度数为( )时,DE∥BC.
A.50° B.60° C.70° D.80°
8.如图,下列条件不能判断直线a∥b的是( )
A.∠1=∠4 B.∠3=∠5
C.∠2+∠5=180° D.∠2+∠4=180°
C
D
9.(淄博中考)如图是一个由4条线段构成的“鱼”形图案,
其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.理由:∵∠1=50°,∠2=50°,∴∠1=∠2,
∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC
10.在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线( )
A.互相垂直 B.互相平行
C.相交 D.相等
11.(2021·永城期末)如图,点E在AC的延长线上,
下列条件中不能判定BD∥AE的是( )
A.∠1=∠2 B.∠3=∠4
C.∠D=∠DCE D.∠A+∠ABD=180°
B
A
12.如图,下列条件:①∠1=∠2;②∠A+∠C=180°;③∠B+∠2=180°且CD∥EF;④∠2+∠3=180°且AB∥EF.其中能判断AB∥CD的有______(填序号).
②③④
13.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°,试说明:AB∥CD.
解:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=∠ACD+∠ACB=70°+60°=130°.
∵∠ABC=50°,∴∠BCD+∠ABC=130°+50°=180°,∴AB∥CD
14.如图,直线EF分别与直线AB,CD相交于点P,Q,PG平分∠APQ,
QH平分∠DQP,且∠1=∠2,找出图中的平行线,并说明理由.
15.如图,直线AB,CD交于点O,OE,OF分别平分∠AOD和∠BOD,
已知∠1+∠2=90°,且∠1∶∠3=1∶8.
(1)求∠AOF的度数;
(2)试说明:AB∥EF.
16.如图,∠B=45°,∠BED=75°,∠D=30°,
猜想AB与CD有怎样的位置关系?并说明理由.
解:AB∥CD.理由:在∠BED内作∠BEF=45°,
则∠B=∠BEF=45°,∴AB∥EF.
∵∠BED=75°,∴∠FED=∠BED-∠BEF=75°-45°=30°,
∴∠FED=∠D=30°,∴EF∥CD,∴AB∥CD
